
第二章平面体系的机动分析 主要讨论平面杆件结构的组成规律和合理形式 §2-1几何构造分析的几个概念 一、平面杆件结构和平面杆件体系 [结构(从几何):一维杆件(平面+空间)、二维平面(板壳、薄壁)、三维空间 (实体)。狭义研究:] 平面杆件结构:两个特点(构筑物、建筑物)简支梁(桥) 1)所有杆件的轴线在一个平面内 2)承担荷载(作用在该平面内)、骨架作用:位置、几何形状不随时间变(不 考虑材料应变) 平面杆件体系几种形式:结合例子 1)几何不变体系:有斜撑的桁架(水平、竖向、力矩) 体系受到任意荷载作用后,若不考虑材料的应变,而能保持其几何形状不变, 位置不变。 静定+超静定:多余联系+全部反力及内力的确定 2)几何可变体系:四连杆机构(筛子)体系受到任意荷载作用后,即使不考虑 材料的应变,其几何形状、位置可变。又有两种形式: 几何常变体系:原为几何可变体系,经微小位移后仍能继续发生刚体运动的几何 可变体系,为。 几何瞬变体系:原为几何可变体系,经微小位移即转化为几何不变体系,称为, 它是可变体系的特殊情况。 如图:施加任意荷载P,变形任意小的0角,由结点2的平衡条件:2Nsin0=P N=P2sin0→co、支座反力c∞ 几何体系划分: 几何不变体系 几何可变体系:几何常变体系 瞬变体系(从不能平衡到平衡的过程中,会产生巨大的内力 或支座反力,使结构破坏,绝对不能应用于工程中)
第二章 平面体系的机动分析 主要讨论平面杆件结构的组成规律和合理形式 §2-1 几何构造分析的几个概念 一、平面杆件结构和平面杆件体系 [结构(从几何):一维杆件(平面+空间)、二维平面(板壳、薄壁)、三维空间 (实体)。狭义研究: ] 平面杆件结构:两个特点(构筑物、建筑物)简支梁(桥) 1)所有杆件的轴线在一个平面内 2)承担荷载(作用在该平面内)、骨架作用:位置、几何形状不随时间变(不 考虑材料应变) 平面杆件体系几种形式:结合例子 1) 几何不变体系:有斜撑的桁架(水平、竖向、力矩) 体系受到任意荷载作用后,若不考虑材料的应变,而能保持其几何形状不变, 位置不变。 静定+超静定:多余联系+全部反力及内力的确定 2) 几何可变体系:四连杆机构(筛子)体系受到任意荷载作用后,即使不考虑 材料的应变,其几何形状、位置可变。又有两种形式: 几何常变体系:原为几何可变体系,经微小位移后仍能继续发生刚体运动的几何 可变体系,为。 几何瞬变体系:原为几何可变体系,经微小位移即转化为几何不变体系,称为, 它是可变体系的特殊情况。 如图:施加任意荷载 P,变形任意小的θ角,由结点 2 的平衡条件:2Nsinθ=P N=P/2sinθ →∞、支座反力→∞ 几何体系划分: 几何不变体系 几何可变体系:几何常变体系 瞬变体系(从不能平衡到平衡的过程中,会产生巨大的内力 或支座反力,使结构破坏,绝对不能应用于工程中)

引出本章三个主要目的:(要解决问题) 1)给定一个体系:不变、可变、瞬变,判定,只有 2)杆件如何拼接成为结构,创造新的合理的结构形式 3)最合理的组成方式,最优 几何组成分析:结构应当承受外荷载,起骨架作用,要求结构的几何组成应当合 理,受载后应保持其几何形状和位置不变(排除材料应变引起的变形)。 杆件结构是由许多杆件组成,而许多杆件组成的体系并不一定是结构。杆件组成 结构应该满足一定的规则。 目的: 1)杆件体系能否作为结构 2)组成结构的规则,杆件如何组合才能成为结构。 3)静定或超静定,确定相应的计算方法 4)多跨结构:基本+附属,确定计算顺序 二、刚片 平面中刚体:几何形状、尺寸(物体内各部分的相对位置)不随时间变化(不考 虑材料应变)。 一根梁、一根杆作为刚片、 扩展:大地(零自由度的刚片)、体系中已经确定为几何不变的部分 三、自由度: 平面体系,从坐标系中一个点扩展 一个动点A(2个自由度), 一个刚片(3个自由度),两个刚片(3+3) 平面体系的自由度:用来确定物体或体系在 平面中的位置时所需要的独立坐标个数(移动坐标和转动坐标) 自由度大于零,肯定几何可变。自由度小于等于零,不一定几何不变。 四、约束(联系) 约束(联系):指阻止或限制体系运动的装置,凡减少一个自由度的装置,称为 个联系(或约束) 1、①一根链杆(活动铰支座):一个约束: ②单较(固定铰支座):两个约束,即相当于两根链杆作用: 虚铰:有限远虚铰 无限远虚铰:(两条平行直线形成的) ③刚结点(固定支座):一个刚性结合相当于三个约束。 ④复铰:联结n个刚片的复饺相当于(m-l)个单铰: ⑤复合刚结点:(n-1)简单刚结点 2、约束分成: 必要约束:为保持体系几何不变必须具有的约束必要约束。能对体系运动起限制 作用,减少体系自由度的装置(限制条件),本身具有这种功能
引出本章三个主要目的:(要解决问题) 1)给定一个体系:不变、可变、瞬变,判定,只有 2)杆件如何拼接成为结构,创造新的合理的结构形式 3)最合理的组成方式,最优 几何组成分析:结构应当承受外荷载,起骨架作用,要求结构的几何组成应当合 理,受载后应保持其几何形状和位置不变(排除材料应变引起的变形)。 杆件结构是由许多杆件组成,而许多杆件组成的体系并不一定是结构。杆件组成 结构应该满足一定的规则。 目的: 1)杆件体系能否作为结构 2)组成结构的规则,杆件如何组合才能成为结构。 3)静定或超静定,确定相应的计算方法 4)多跨结构:基本+附属,确定计算顺序 二、刚片 平面中刚体:几何形状、尺寸(物体内各部分的相对位置)不随时间变化(不考 虑材料应变)。 一根梁、一根杆作为刚片、 扩展:大地(零自由度的刚片)、体系中已经确定为几何不变的部分 三、自由度: 平面体系,从坐标系中一个点扩展 一个动点 A(2 个自由度), 一个刚片(3 个自由度),两个刚片(3+3) 平面体系的自由度:用来确定物体或体系在 平面中的位置时所需要的独立坐标个数(移动坐标和转动坐标) 自由度大于零,肯定几何可变。自由度小于等于零,不一定几何不变。 四、约束(联系) 约束(联系):指阻止或限制体系运动的装置,凡减少一个自由度的装置,称为一 个联系(或约束)。 1、①一根链杆(活动铰支座):一个约束; ②单铰(固定铰支座):两个约束,即相当于两根链杆作用; 虚铰:有限远虚铰 无限远虚铰:(两条平行直线形成的) ③刚结点(固定支座):一个刚性结合相当于三个约束。 ④复铰:联结 n 个刚片的复铰相当于(n-1)个单铰; ⑤复合刚结点:(n-1)简单刚结点 2、约束分成: 必要约束:为保持体系几何不变必须具有的约束必要约束。能对体系运动起限制 作用,减少体系自由度的装置(限制条件),本身具有这种功能

多余约束:如果在一个体系中增加一个约束,而体系的自由度并不因而减少,则 此约束称为多余约束。(未发挥应有的作用):不能减少体系自由度的约束。相对 性,起作用,静定+超静定,(三个台阶)(比较弯矩图)。增加安全度。 注:只有必要约束对体系的自由度有影响,而多余约束则对体系的自由度没有影 响。 五、计算自由度: 一个平面体系,通常由若干刚片彼此铰结并用支座链杆与基础相联而成。 刚片数m(member,)单较数h(hinge)),支座链杆数r(rod),则: W(计算自由度(自由度总数)(联系总数),即: w=3*m-(2h+n) 注:h只包括刚片与刚片之间相互连接所用的铰,不包括刚片与支承链杆相连 用的较。 若为铰结链杆体系,即完全由两端铰结的杆件组成,则: j:结点数,b:杆件数,:支座链杆数,则: w=2j-(b+r) 1、W>0,缺少足够的联系,几何可变: 2、W=0,体系具备几何不变所必需的最少联系数目 3、W<0,体系有多余联系 4、若体系与基础不连,体系内部几何不变的必要条件是体系内部的自由度V≤3 结论:W≤0(或V≤3)不一定就是几何不变的。因为尽管联系数目足够多甚至还 有多余,但若布置不当,则仍可能是可变的。 →W≤0(或V≤3)只是几何不变体系的必要条件,还不是充分条件。 如: &&上 W=0情况 81R W=一1情况 §2-2几何不变结构杆系的组成规律 一、组成规律: 三角形规律:如果三个铰不共线,则一个较结三角形的形状是不变的,而且 没有多余约束。 1、三刚片的联结方式(三刚片规则):三刚片用不在同一直线上的三个单铰两两 铰联,则组成几何不变体系,且无多余约束。 推论1:三刚片用六根链杆两两相联,若三个瞬铰的转动中心不在同一直线 上,则组成几何不变体系,且无多余约束。 2、两刚片之间的联结方式(二刚片规则):两刚片用一个铰和一根不通过此铰的 链杆相联,则组成几何不变体系,且无多余约束
多余约束:如果在一个体系中增加一个约束,而体系的自由度并不因而减少,则 此约束称为多余约束。(未发挥应有的作用):不能减少体系自由度的约束。相对 性,起作用,静定+超静定,(三个台阶)(比较弯矩图)。增加安全度。 注:只有必要约束对体系的自由度有影响,而多余约束则对体系的自由度没有影 响。 五、计算自由度: 一个平面体系,通常由若干刚片彼此铰结并用支座链杆与基础相联而成。 刚片数 m(member),单铰数 h(hinge),支座链杆数 r(rod),则: W(计算自由度)=(自由度总数)-( 联系总数),即: w=3*m-(2h+r) 注:h 只包括刚片与刚片之间相互连接所用的铰,不包括刚片与支承链杆相连 用的铰。 若为铰结链杆体系,即完全由两端铰结的杆件组成,则: j:结点数,b:杆件数,r:支座链杆数,则: w=2j-(b+r) 1、W>0,缺少足够的联系,几何可变; 2、W=0,体系具备几何不变所必需的最少联系数目 3、W<0,体系有多余联系 4、若体系与基础不连,体系内部几何不变的必要条件是体系内部的自由度 V≤3 结论:W≤0(或 V≤3)不一定就是几何不变的。因为尽管联系数目足够多甚至还 有多余,但若布置不当,则仍可能是可变的。 →W≤0 (或 V≤3)只是几何不变体系的必要条件,还不是充分条件。 如: W=0 情况 W=-1 情况 §2-2 几何不变结构杆系的组成规律 一、组成规律: 三角形规律:如果三个铰不共线,则一个铰结三角形的形状是不变的,而且 没有多余约束。 1、三刚片的联结方式(三刚片规则):三刚片用不在同一直线上的三个单铰两两 铰联,则组成几何不变体系,且无多余约束。 推论 1:三刚片用六根链杆两两相联,若三个瞬铰的转动中心不在同一直线 上,则组成几何不变体系,且无多余约束。 2、两刚片之间的联结方式(二刚片规则):两刚片用一个铰和一根不通过此铰的 链杆相联,则组成几何不变体系,且无多余约束

推论2:两刚片用三根不全平行也不交于一点的链杆相联,则组成几何不变 体系,且无多余约束。 3、一个点和一个刚片之间联结方式(二元体规则):一个刚片与一个结点用两根 链杆直连,且三个铰不在一直线上,则组成几何不变体系,且无多余约束。 二元体:两根不共线链杆联结一个结点的装置为二元体: 推论3:在一个体系上增加一个二元体或拆除一个二元体,不会改变原有体 系的几何构造性质(由于增加一个点即增加了2个自由度,但是不两线的二 链杆提供了2个约束)常应用于“桁架结构” 二、组成规则说明: 1、这些组成规律,主要有三点: 1).三角形规律的理解:三个规律是相互勾通的。 2)·点、刚片的概念: 3).约束的概念及各种约束的等效代换关系:由于两根链杆的约束作用相 当于一个瞬较的约束作用,因此上述规律中的每一个较都可以用相应的两根链杆 来替换。 2、三个组成规律分别对应于三种基本的几何组成方式。若把某一刚片看作基础, 则。 3、不满足规则 (1)三个规则说明了组成无多余联系的几何不变体系所需的最少联系。如在这 些必要联系的基础上再增加联系,增加的联系为多余联系,成为超静定结 构。如若刚片之间的联系少于三个规则所要求的数目,肯定几何可变。 (2)两刚片之间用全交于一实铰的三链杆相连,几何可变 (3)两刚片之间用全交于一虚铰的三链杆相连(延长线交于一点),几何瞬变。 (4)两刚片之间用三根平行但不等长的链杆相连,瞬变体系 (5)两刚片之间用三根平行且等长的链杆相连,可变体系。 (6)三刚片用位于同一直线上的三个单铰(实铰或虚铰)两两相连,瞬变体系。 4、虚铰在无限远处情况 ①一个虚较在无限远处:若三个刚片用两个实较与一个无限远处虚铰相联结, 若形成虚铰的二平行链杆不与两实铰边线平行,则形成几何不变体:否则, 为几何可变体。 ②两虚铰在无限远处:若三刚片用三铰相联结中的两个虚铰在无限远处,当形 成两个虚铰的四根链杆互不平行,则为几何不变体系:当四根链杆互相平行, 为瞬变体系:若四链杆等长平行,为常变体系。 ③三虚较在无限远处:三刚片分别用三对任意方向的平行链杆相联,均为瞬变 体系:若三对平行链杆各自等长,则为几何常变体系
推论 2:两刚片用三根不全平行也不交于一点的链杆相联,则组成几何不变 体系,且无多余约束。 3、一个点和一个刚片之间联结方式(二元体规则):一个刚片与一个结点用两根 链杆直连,且三个铰不在一直线上,则组成几何不变体系,且无多余约束。 二元体:两根不共线链杆联结一个结点的装置为二元体; 推论 3:在一个体系上增加一个二元体或拆除一个二元体,不会改变原有体 系的几何构造性质(由于增加一个点即增加了 2 个自由度,但是不两线的二 链杆提供了 2 个约束)常应用于“桁架结构” 二、组成规则说明: 1、这些组成规律,主要有三点: 1). 三角形规律的理解:三个规律是相互勾通的。 2). 点、刚片的概念; 3). 约束的概念及各种约束的等效代换关系:由于两根链杆的约束作用相 当于一个瞬铰的约束作用,因此上述规律中的每一个铰都可以用相应的两根链杆 来替换。 2、三个组成规律分别对应于三种基本的几何组成方式。若把某一刚片看作基础, 则。 3、不满足规则 (1)三个规则说明了组成无多余联系的几何不变体系所需的最少联系。如在这 些必要联系的基础上再增加联系,增加的联系为多余联系,成为超静定结 构。如若刚片之间的联系少于三个规则所要求的数目,肯定几何可变。 (2)两刚片之间用全交于一实铰的三链杆相连,几何可变。 (3)两刚片之间用全交于一虚铰的三链杆相连(延长线交于一点),几何瞬变。 (4)两刚片之间用三根平行但不等长的链杆相连,瞬变体系。 (5)两刚片之间用三根平行且等长的链杆相连,可变体系。 (6)三刚片用位于同一直线上的三个单铰(实铰或虚铰)两两相连,瞬变体系。 4、虚铰在无限远处情况 ① 一个虚铰在无限远处:若三个刚片用两个实铰与一个无限远处虚铰相联结, 若形成虚铰的二平行链杆不与两实铰边线平行,则形成几何不变体;否则, 为几何可变体。 ② 两虚铰在无限远处:若三刚片用三铰相联结中的两个虚铰在无限远处,当形 成两个虚铰的四根链杆互不平行,则为几何不变体系;当四根链杆互相平行, 为瞬变体系;若四链杆等长平行,为常变体系。 ③ 三虚铰在无限远处:三刚片分别用三对任意方向的平行链杆相联,均为瞬变 体系;若三对平行链杆各自等长,则为几何常变体系
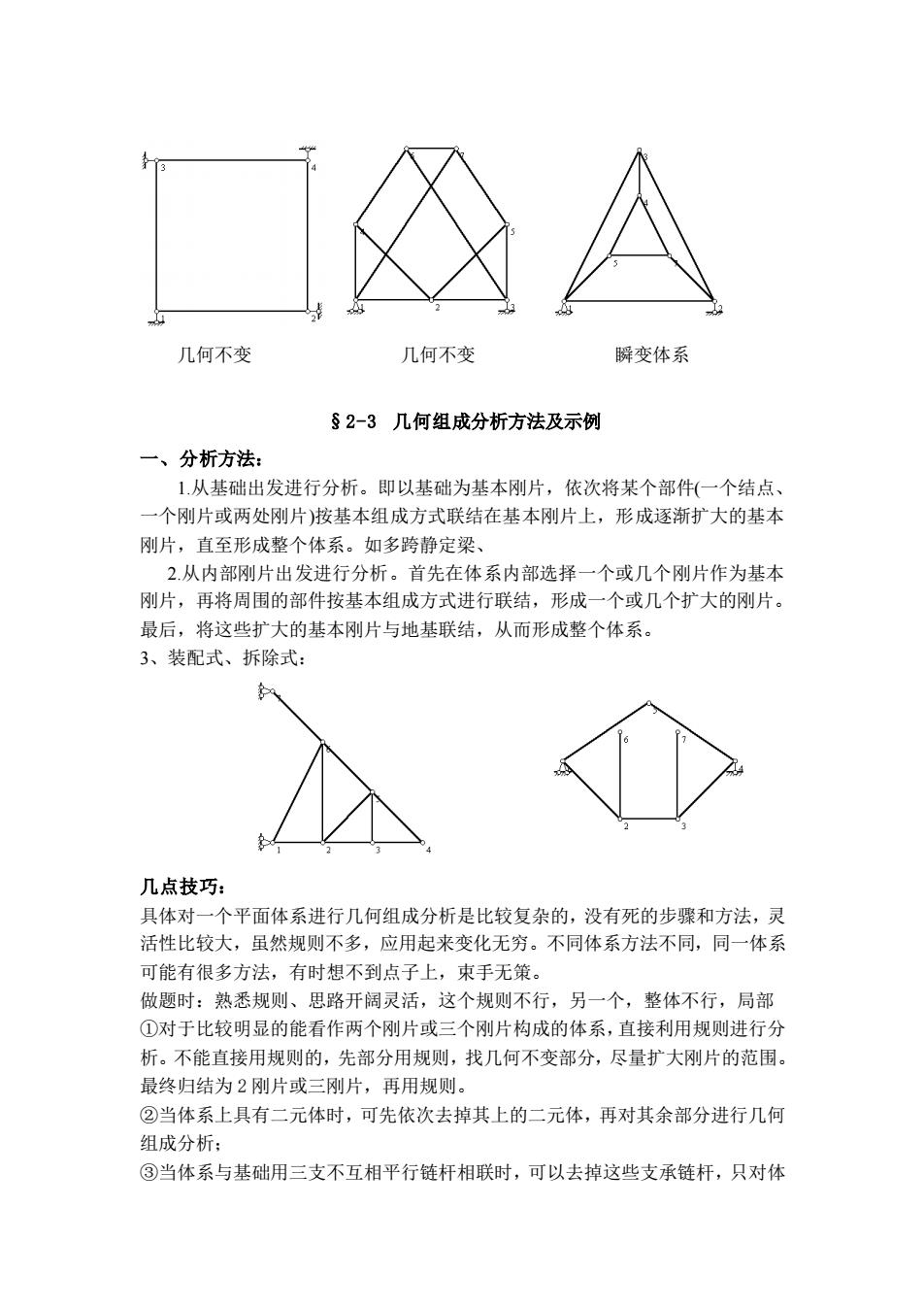
几何不变 几何不变 瞬变体系 §2-3几何组成分析方法及示例 一、分析方法: 1从基础出发进行分析。即以基础为基本刚片,依次将某个部件(一个结点、 一个刚片或两处刚片)按基本组成方式联结在基本刚片上,形成逐渐扩大的基本 刚片,直至形成整个体系。如多跨静定梁、 2.从内部刚片出发进行分析。首先在体系内部选择一个或几个刚片作为基本 刚片,再将周围的部件按基本组成方式进行联结,形成一个或几个扩大的刚片。 最后,将这些扩大的基本刚片与地基联结,从而形成整个体系。 3、装配式、拆除式: 几点技巧: 具体对一个平面体系进行几何组成分析是比较复杂的,没有死的步骤和方法,灵 活性比较大,虽然规则不多,应用起来变化无穷。不同体系方法不同,同一体系 可能有很多方法,有时想不到点子上,束手无策。 做题时:熟悉规则、思路开阔灵活,这个规则不行,另一个,整体不行,局部 ①对于比较明显的能看作两个刚片或三个刚片构成的体系,直接利用规则进行分 析。不能直接用规则的,先部分用规则,找几何不变部分,尽量扩大刚片的范围 最终归结为2刚片或三刚片,再用规则。 ②当体系上具有二元体时,可先依次去掉其上的二元体,再对其余部分进行几何 组成分析: ③当体系与基础用三支不互相平行链杆相联时,可以去掉这些支承链杆,只对体
几何不变 几何不变 瞬变体系 §2-3 几何组成分析方法及示例 一、分析方法: 1.从基础出发进行分析。即以基础为基本刚片,依次将某个部件(一个结点、 一个刚片或两处刚片)按基本组成方式联结在基本刚片上,形成逐渐扩大的基本 刚片,直至形成整个体系。如多跨静定梁、 2.从内部刚片出发进行分析。首先在体系内部选择一个或几个刚片作为基本 刚片,再将周围的部件按基本组成方式进行联结,形成一个或几个扩大的刚片。 最后,将这些扩大的基本刚片与地基联结,从而形成整个体系。 3、装配式、拆除式: 几点技巧: 具体对一个平面体系进行几何组成分析是比较复杂的,没有死的步骤和方法,灵 活性比较大,虽然规则不多,应用起来变化无穷。不同体系方法不同,同一体系 可能有很多方法,有时想不到点子上,束手无策。 做题时:熟悉规则、思路开阔灵活,这个规则不行,另一个,整体不行,局部 ①对于比较明显的能看作两个刚片或三个刚片构成的体系,直接利用规则进行分 析。不能直接用规则的,先部分用规则,找几何不变部分,尽量扩大刚片的范围。 最终归结为 2 刚片或三刚片,再用规则。 ②当体系上具有二元体时,可先依次去掉其上的二元体,再对其余部分进行几何 组成分析; ③当体系与基础用三支不互相平行链杆相联时,可以去掉这些支承链杆,只对体

系本身进行分析 ④当体系与基础用多于三支链杆相联时,则必须将基础视为刚片,以整个体系包 括基础进行分析 ⑤注意虚铰的应用,两根链杆等价于一个单铰,使结构变得比较简洁对体系进行 ©几何组成分析时,可利用等效代换的概念使问题得到简化: 联结两刚片的链杆可用其交点的虚铰代替: 一几何不变部分可视为一个刚片: 复杂形状的链杆(如曲链杆、折链杆)可看作通过铰心的直链杆: (14、36等效为链杆、)几何瞬变体系 [三刚片:上部体系选刚片一定要均匀且和地基合适联系] 学习方法和思路:多角度多思维,正规则,反规则,满足和不满足。同一问题多 种方法。不同问题同一方法。多种不同结构形式。】 X☒K 几何瞬变体系 几何瞬变体系 二、示例 瞬变体系 瞬变体系(共线或接近共线) 休系 几何不变无多余约束体系几何不变无多余约束体系
系本身进行分析; ④当体系与基础用多于三支链杆相联时,则必须将基础视为刚片,以整个体系包 括基础进行分析 ⑤注意虚铰的应用,两根链杆等价于一个单铰,使结构变得比较简洁对体系进行 ⑥几何组成分析时,可利用等效代换的概念使问题得到简化: 联结两刚片的链杆可用其交点的虚铰代替: 一几何不变部分可视为一个刚片; 复杂形状的链杆(如曲链杆、折链杆)可看作通过铰心的直链杆; (14、36 等效为链杆、)几何瞬变体系 [三刚片:上部体系选刚片一定要均匀且和地基合适联系] 学习方法和思路:多角度多思维,正规则,反规则,满足和不满足。同一问题多 种方法。不同问题同一方法。多种不同结构形式。] 几何瞬变体系 几何瞬变体系 二、示例: 瞬变体系 瞬变体系(共线或接近共线) 瞬变体系 几何不变无多余约束体系 几何不变无多余约束体系

§2-4几何组成与静定性的关系 平面杆件体系:几何不变体系 几何可变体系:常变体系 瞬变体系 常变体系: 在任意荷载作用下,都不能维持平衡并会发生运动,因此常变体系没有静力学 解答。 几何不变体系: 多余约束:是超静定结构:多余约束不是固定不变的,在几何不 变的前提下,可以任意选取,但不管如 何选取,其多余约束数目不变。 无多余约束:静定结构 瞬变体系: 在荷载作用下,反力和内力将是无穷大,或是不定式。 所以: ①无多余约束的几何不变体系是静定结构: ②有多余约束的几何不变体系是超静定结构; ③常变体系不存在静力学解答,瞬变体系不存在有限或确定的静力学 解答,即:几何可变体系不能作为结构使用
§2-4 几何组成与静定性的关系 平面杆件体系:几何不变体系 几何可变体系:常变体系 瞬变体系 常变体系: 在任意荷载作用下,都不能维持平衡并会发生运动,因此常变体系没有静力学 解答。 几何不变体系: 多余约束:是超静定结构;多余约束不是固定不变的,在几何不 变的前提下,可以任意选取,但不管如 何选取,其多余约束数目不变。 无多余约束:静定结构 瞬变体系: 在荷载作用下,反力和内力将是无穷大,或是不定式。 所以: ① 无多余约束的几何不变体系是静定结构; ②有多余约束的几何不变体系是超静定结构; ③常变体系不存在静力学解答,瞬变体系不存在有限或确定的静力学 解答,即:几何可变体系不能作为结构使用