
第七章力法 一.基本概念 力法是计算超静定结构的最基本方法。 力法的基本思路是把超静定结构的计算问题转化为静定结构的计算问题。 力法的基本结构一一静定结构 力法的基本未知量一一结构中的多余未知力 力法的基本方程一一反映位移条件的变形协调方程 下面结合实例说明力法的基本思路和原理 图7-1为一次超静定结构,如果撒去B处的支座链杆并用未知力,代替变成了图7-1b所示的静定结 构,这样就得到了含有多余未知力的静定结构,此结构称为力法的基本体系(基本体系并不唯一)。相应的 把原超静定结构中多余约束和荷载都去掉后得到的静定结构称为力法的基本结构图7-1©。 9山通送 原结构 () 出 y X B 基本体系 基本结构 图7-1 这样通过把多余约束去掉用多余未知力来代替,将超静定结构变为静定结构,解题的关键就是多余未知 力的求解问题, 这也是力法的第一个特点 把多余未知力的计算问题当作超静定问题的关健,把多余未知力当作关健地位的未知力 —一力法的基本 未知量 下面将讨论如何建立力法方程来求解基本未知量: 为了求解多余的未知力,显然静力平衡方程式不能够求解,必须建立新的方程。 第一步:去掉原结构的多余约束,代之以多余未知力,得到静定的基本体系。 第二步:基 体系 原结构的变形相同,特别是基 系上与多余未知力相应的位移与原超静定结构 多余约束处的位移条件一致,这是确定多余未知力大小的依据。一般情况下,当原结构上在多余约束处没有 支座位移时,则基本体系应满足的变形条件是:与多余未知力相应的位移为零。 下面按照以上思路具体求解图T-1所示的超静定结构
第七章 力法 一. 基本概念 力法是计算超静定结构的最基本方法。 力法的基本思路是把超静定结构的计算问题转化为静定结构的计算问题。 力法的基本结构——静定结构 力法的基本未知量——结构中的多余未知力 力法的基本方程——反映位移条件的变形协调方程 下面结合实例说明力法的基本思路和原理 图 7-1a 为一次超静定结构,如果撤去 B 处的支座链杆并用未知力 X1 代替变成了图 7-1b 所示的静定结 构,这样就得到了含有多余未知力的静定结构,此结构称为力法的基本体系(基本体系并不唯一)。相应的 把原超静定结构中多余约束和荷载都去掉后得到的静定结构称为力法的基本结构图 7-1c。 图 7-1 这样通过把多余约束去掉用多余未知力来代替,将超静定结构变为静定结构,解题的关键就是多余未知 力的求解问题,这也是力法的第一个特点: 把多余未知力的计算问题当作超静定问题的关键,把多余未知力当作关键地位的未知力-力法的基本 未知量 下面将讨论如何建立力法方程来求解基本未知量: 为了求解多余的未知力,显然静力平衡方程式不能够求解,必须建立新的方程。 第一步:去掉原结构的多余约束,代之以多余未知力,得到静定的基本体系。 第二步:基本体系和原结构的变形相同,特别是基本体系上与多余未知力相应的位移与原超静定结构上 多余约束处的位移条件一致,这是确定多余未知力大小的依据。一般情况下,当原结构上在多余约束处没有 支座位移时,则基本体系应满足的变形条件是:与多余未知力相应的位移为零。 下面按照以上思路具体求解图 7-1a 所示的超静定结构
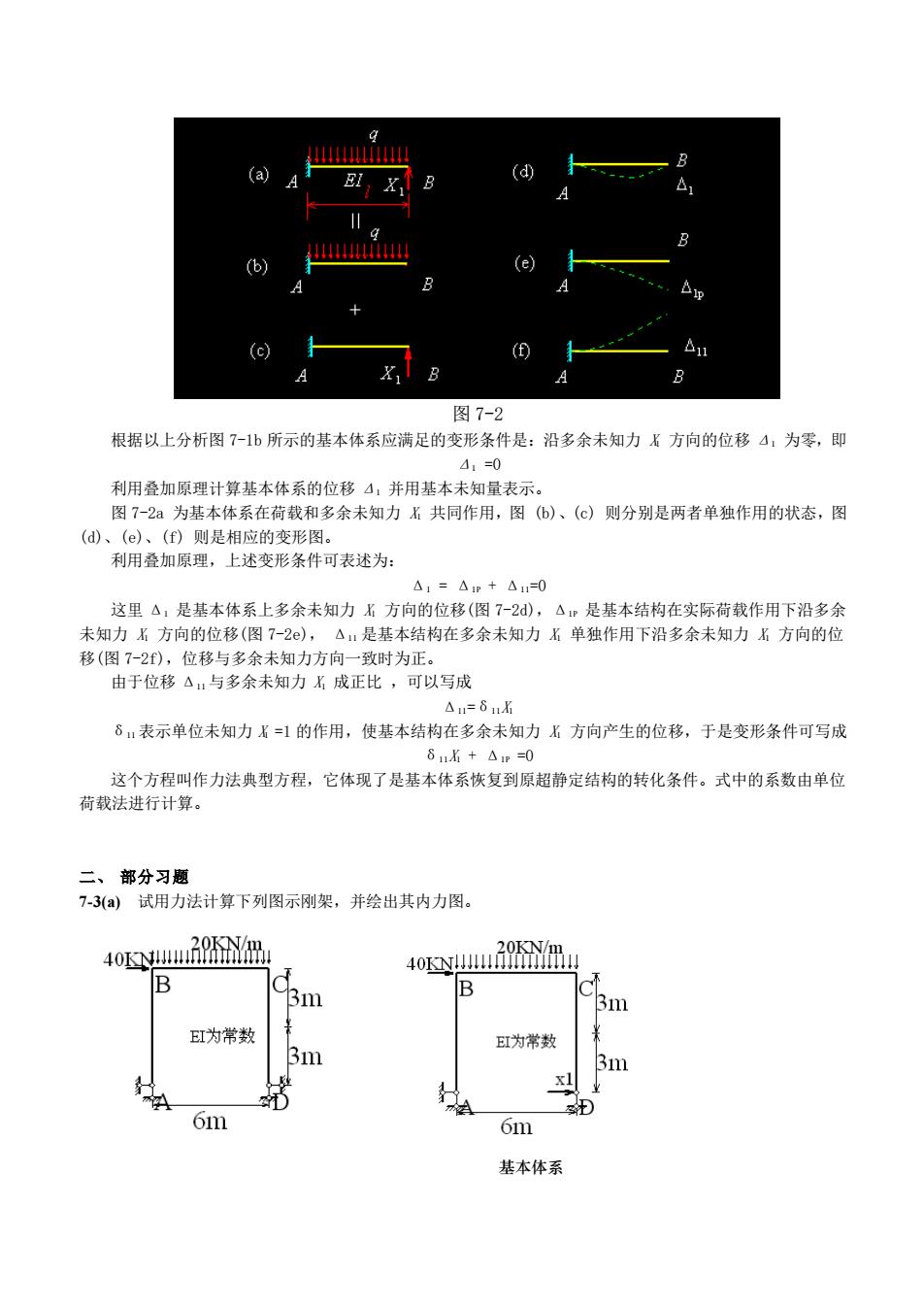
(a 4 (④ (6) (c) (0 图7-2 根据以上分析图7-1b所示的基本体系应满足的变形条件是:沿多余未知力方向的位移4:为零,即 4:-0 利用叠加原理计算基本体系的位移4:并用基本未知量表示。 图7-2a为基本体系在荷载和多余未知力x共同作用,图(6)、()则分别是两者单独作用的状态,图 (d)、(e)、(f)则是相应的变形图。 利用叠加原理, 上述变形条件可表述为: △1=△1p+△1=0 这里△,是基本体系上多余未知力X方向的位移(图7-2),△是基本结构在实际荷载作用下沿多余 未知力黑方向的位移(图7-2),△:是基本结构在多余未知力君单独作用下沿多余未知力屠方向的位 移(图7-2),位稳与多金未知力方向一致时为正。 由于位移△与多余未知力X成正比,可以写成 △=8n δ表示单位未知力X=1的作用,使基本结构在多余未知力:方向产生的位移,于是变形条件可写成 61X+△m=0 这个方程叫作力法典型方程,它体现了是基本体系恢复到原超静定结构的转化条件。式中的系数由单位 荷都法讲行计算】 二、部分习题 7-3()试用力法计算下列图示刚架,并绘出其内力图。 40K9K 40KN 不 3m EI为常数 31m E豇为常数 31m 61m 6m 基本体系
图 7-2 根据以上分析图 7-1b 所示的基本体系应满足的变形条件是:沿多余未知力 X1 方向的位移 Δ1 为零,即 Δ1 =0 利用叠加原理计算基本体系的位移 Δ1 并用基本未知量表示。 图 7-2a 为基本体系在荷载和多余未知力 X1 共同作用,图 (b)、(c) 则分别是两者单独作用的状态,图 (d)、(e)、(f) 则是相应的变形图。 利用叠加原理,上述变形条件可表述为: Δ1 = Δ1P + Δ11=0 这里 Δ1 是基本体系上多余未知力 X1 方向的位移(图 7-2d),Δ1P 是基本结构在实际荷载作用下沿多余 未知力 X1 方向的位移(图 7-2e), Δ11 是基本结构在多余未知力 X1 单独作用下沿多余未知力 X1 方向的位 移(图 7-2f),位移与多余未知力方向一致时为正。 由于位移 Δ11 与多余未知力 X1 成正比 ,可以写成 Δ11=δ11X1 δ11 表示单位未知力 X1 =1 的作用,使基本结构在多余未知力 X1 方向产生的位移,于是变形条件可写成 δ11X1 + Δ1P =0 这个方程叫作力法典型方程,它体现了是基本体系恢复到原超静定结构的转化条件。式中的系数由单位 荷载法进行计算。 二、 部分习题 7-3(a) 试用力法计算下列图示刚架,并绘出其内力图。 基本体系
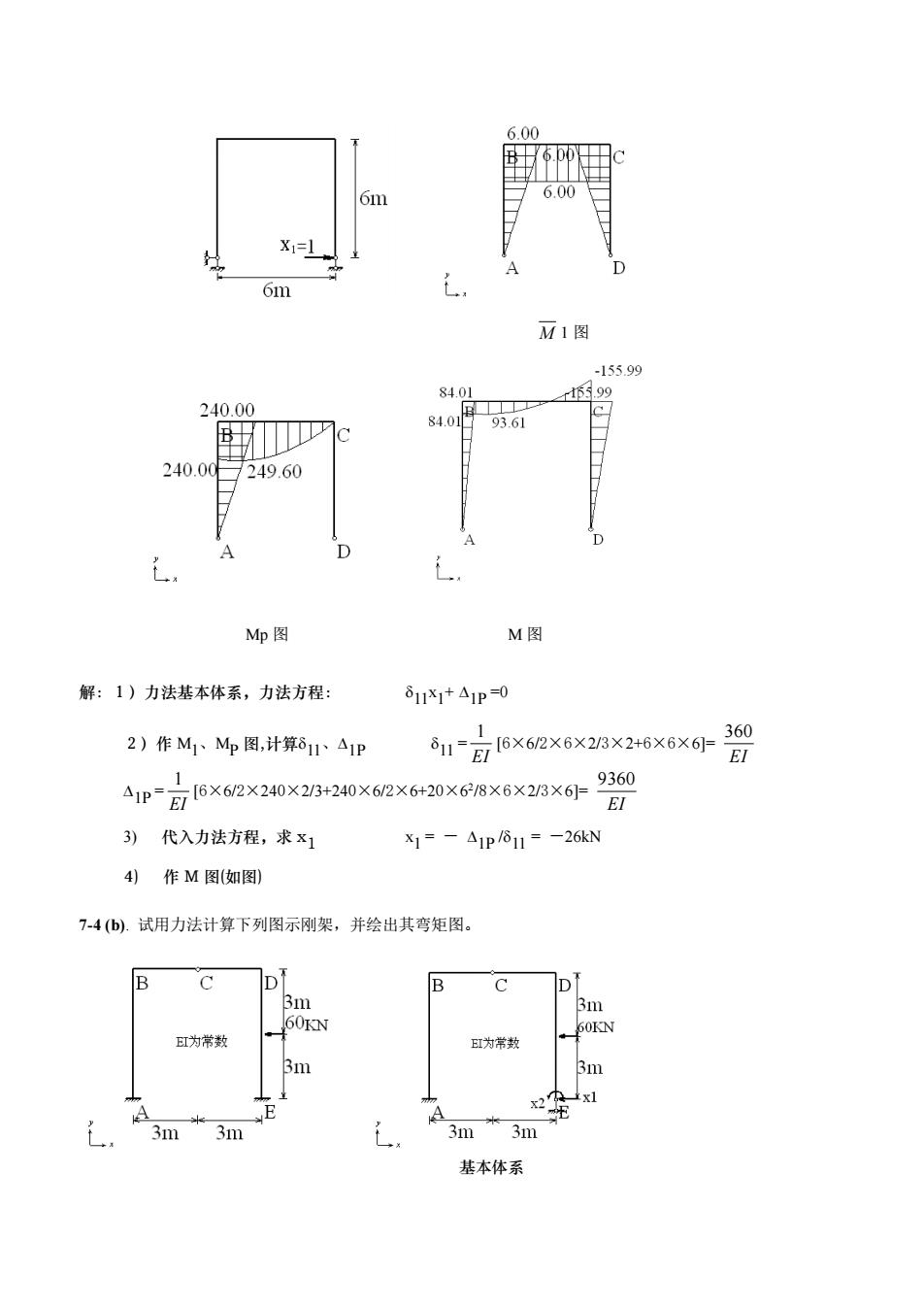
6.00 6.00日 61m M1图 84.01 84.01f 249.60 Mp图 M图 解:1)力法基本体系,力法方程: 811x1+A1P=0 2)作M个、4图,计算01、41p81=司I6x62×6x23x2+6x6×6-360 △1p-E6×62×240x213+240×62x6+20X68×6×23X6-9360 3)代入力法方程,求x1 X1=-△1P/61=-26N 4作M图(如图) 7-4(b).试用力法计算下列图示刚架,并绘出其弯矩图。 3m 3m 3m 基本体系
M 1 图 Mp 图 M 图 解:1)力法基本体系,力法方程: 11x 1 + 1P =0 2)作 M1、MP 图,计算 11、1P 11 = 1 EI [6×6/2×6×2/3×2+6×6×6]= 360 EI 1P = 1 EI [6×6/2×240×2/3+240×6/2×6+20×6 2 /8×6×2/3×6]= 9360 EI 3) 代入力法方程,求 x1 x 1 = - 1P / 11 = -26kN 4) 作 M 图(如图) 7-4 (b). 试用力法计算下列图示刚架,并绘出其弯矩图。 基本体系
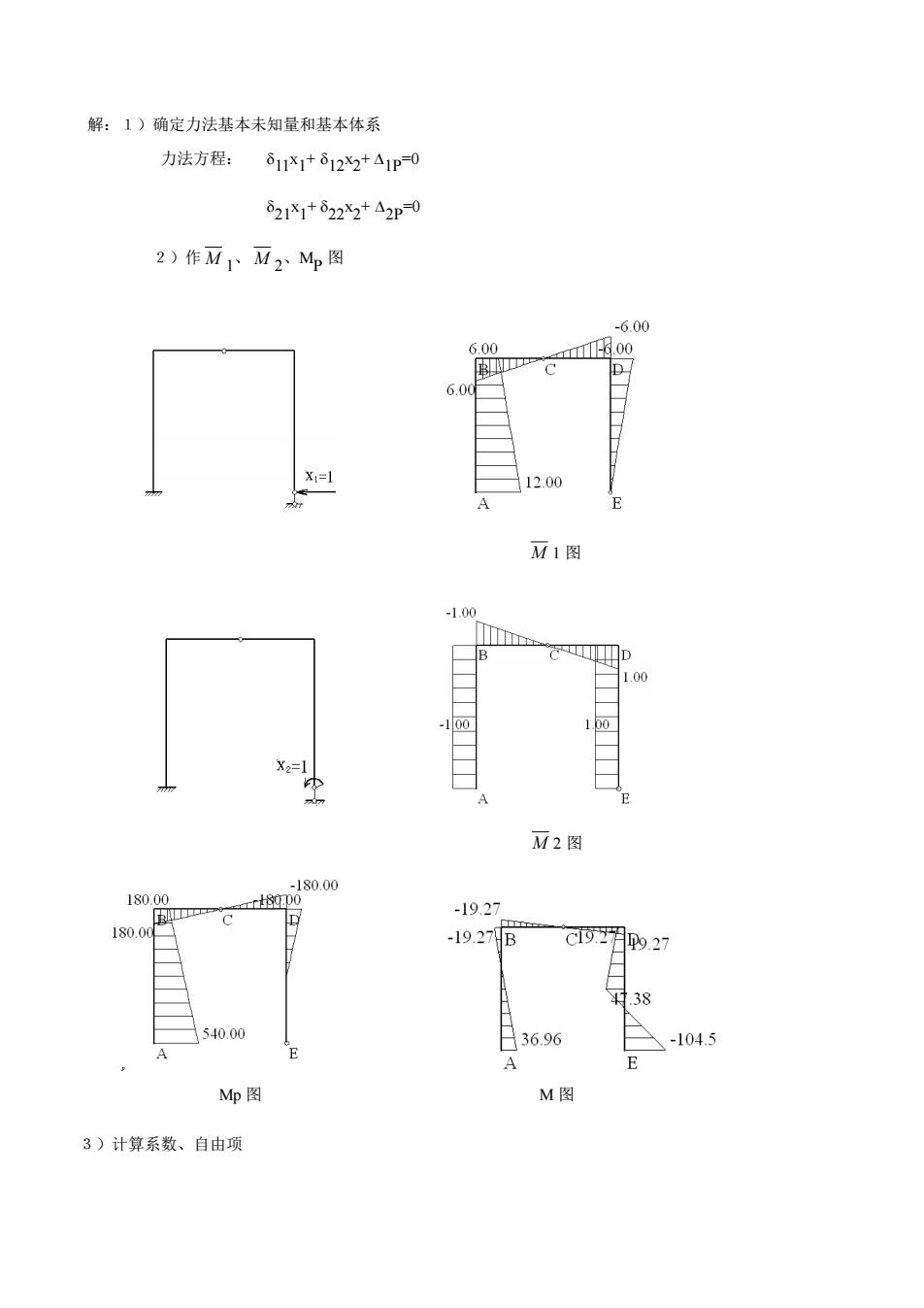
解:1)确定力法基本未知量和基本体系 力法方程:811X1+812X2+A1p0 0211+8222+42P0 2)作M1M2M图 6.00 xi= 12.00 M1图 10 TU .0 M2图 180.0 180.0 -1927 180 19.27B c91月p9.27 154000 日36.96 -104.5 Mp图 M图 3)计算系数、自由项
解:1)确定力法基本未知量和基本体系 力法方程: 11x 1 + 12x 2 + 1P=0 21x 1 + 22x 2 + 2P=0 2)作 M 1、 M 2、MP 图 M 1 图 M 2 图 Mp 图 M 图 3)计算系数、自由项
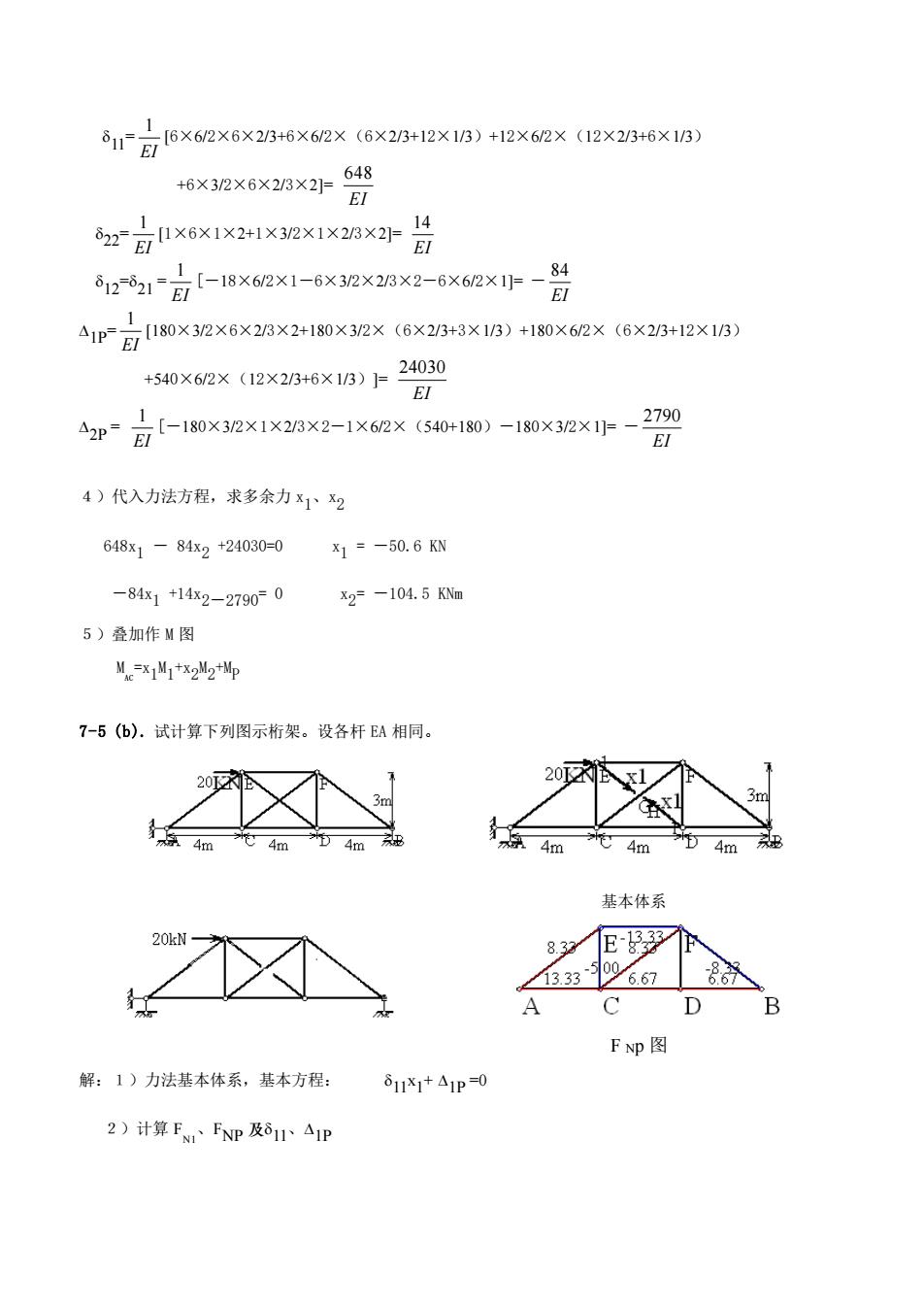
A言x62x6x266X62x6x2r12x1B)+12x62x42x20-6X16 +6×32X6×2BX2648 gx6xix2 KJX1XJ3XH告 5p1日-1sx0w2x1-6x30xax2-6x6eXIp- 1 +50x62×2x296x18上200 p言-10x32x1xaex2-1 XX(-10)-1s0x30xI小-2 4)代入力法方程,求多余力x12 648x1-84x2+24030-0X1=-50.6KN -84x1+14x2-27900 x2-104.5K 5)叠加作M图 M=X1M1+22p 7-5(b).试计算下列图示桁架。设各杆EA相同。 20 4m光4m4m 基本体系 83E 6326686 FNP图 解:1)力法基本体系,基本方程: 811X1+△1p=0 2)计算FFNP及81△1P
11= 1 EI [6×6/2×6×2/3+6×6/2×(6×2/3+12×1/3)+12×6/2×(12×2/3+6×1/3) +6×3/2×6×2/3×2]= 648 EI 22= 1 EI [1×6×1×2+1×3/2×1×2/3×2]= 14 EI 12= 21 = 1 EI [-18×6/2×1-6×3/2×2/3×2-6×6/2×1]= - 84 EI 1P= 1 EI [180×3/2×6×2/3×2+180×3/2×(6×2/3+3×1/3)+180×6/2×(6×2/3+12×1/3) +540×6/2×(12×2/3+6×1/3)]= 24030 EI 2P = 1 EI [-180×3/2×1×2/3×2-1×6/2×(540+180)-180×3/2×1]= - 2790 EI 4)代入力法方程,求多余力 x 1、x 2 648x 1 - 84x 2 +24030=0 x1 = -50.6 KN -84x 1 +14x 2-2790= 0 x2 = -104.5 KNm 5)叠加作 M 图 M AC =x1 M 1 +x2 M 2 +MP 7-5 (b). 试计算下列图示桁架。设各杆 EA 相同。 基本体系 F Np 图 解:1)力法基本体系,基本方程: 11x 1 + 1P =0 2)计算 F N1 、FNP 及 11、1P

δ11=ΣFN12EA=(0.8X4X2+0.6×3×2+1X5×2)yEA=17.28/EA △IP=ΣFNI FNPUEA =0.8×13.33×4-0.8×6.67×4+0.6×5×3+1×8.33×5)EA=71.96/EA 3)代入力法方程中,求解x1 x1=-△1P611=-4.17KN 4)叠加计算各杆轴力 FN-FNIX1+FNP X1=1 r-0.d 06-0.8D0 F图 D B FN图 7-11.试绘出图示连续梁的M图,并作校核。已知I=36×10m,E=3×10'kPa h209 4m 4m 4m 4m4m4m 基本体系
11 = ∑FN1 2 l/EA= (0.82×4×2+0.62×3×2+12×5×2)/EA=17.28/EA 1P = ∑FN1 FNPl/EA =(0.8×13.33×4-0.8×6.67×4+0.6×5×3+1×8.33×5)/EA=71.96/EA 3)代入力法方程中,求解 x1 x1 = — 1P /11 = —4.17KN 4) 叠加计算各杆轴力 FN =FN1x1 +FNP FN1 图 F N 图 7-11.试绘出图示连续梁的 M 图,并作校核。已知 I=36×10-4 m 4 ,E=3×107 kPa 基本体系

-2.67-2.67, cWii格.-33 B 4m* 4m* 4m M1图 52.67-2.67 -13多p B 4细4细4细一 M2图 1)确定力法基本未知量和基本体系 力法方程:111+612*2+△1-0.02 821X1+822X2+A20 1合267×42×2.67×2B+2.67×82×267x232852 i2可2.67×42X2.67×23+2.67x82x267X2B 28.52 EI 812621267×42X1.3x2x22.67X42x1.3x2/32.67X1/3) H.3x42X1.3X1/32.67x23)F2487 EI A1=.r91 △1-0 X2=275.66KN:x1=-316.12KN A2=-r91 42-0 -313.60-313.60 HD C D 475.44475.44 M图
M 1 图 M 2 图 1)确定力法基本未知量和基本体系 力法方程: 11x 1 + 12x 2 + 1 =-0.02 21x 1 + 22x 2 + 2 =0 11= 1 EI [2.67×4/2×2.67×2/3+2.67×8/2×2.67×2/3]= 28.52 EI 22= 1 EI [2.67×4/2×2.67×2/3+2.67×8/2×2.67×2/3]= 28.52 EI 12= 21 = 1 EI [2.67×4/2×1.33×2/3×2+2.67×4/2×(1.33×2/3+2.67×1/3) +1.33×4/2×(1.33×1/3+2.67×2/3)]= 24.87 EI = -∑r i c i 1 =0 x2=275.66KN; x1=-316.12KN = -∑r i c i 2 =0 M 图