
第四章实体三铰拱 §4-1概述 1、拱式结构的特征及应用: 应用:门、窗、桥、巷道、窑洞 特征:杆轴是曲线,竖向荷载作用下有水平推力。和曲梁比较 三铰拱是由两条曲杆用铰相互联结,并各自与支座用铰相联结而成。 优点:在竖向荷载作用下拱存在水平推力作用,导致其所受的弯矩远比梁小,压力也比 较均匀:若合理选择拱轴,弯矩为0,主要承受压力。 缺点:需要坚固而强大的地基基础来支承: 2、拱的形式: 静定结构:三铰拱。有两种形式:无拉杆三铰拱、有拉杆的三铰拱、及其变化形式、 做成折线即为三较刚架 超静定结构:无铰拱、两铰拱 3、各部分名称: 跨度L、 拱高:拱顶到两支承边线距离, 拱脚铰、拱顶铰 对称拱、斜拱(不对称拱) :矢跨比(高跨比)。高跨比对拱的主要性能有比较大的影响(1一110)。若f→0, 三铰共线或接近共线,瞬变体系。 4、计算方法: 数解法、图解法 §4-2三铰拱的数解法 竖向荷载作用下三铰平拱的支座反力和内力的计算公式,并和同跨同荷载的相应简 支梁比较。 一、支座反力的计算: 三铰拱 三铰拱相当梁:
第四章 实体三铰拱 §4-1 概述 1、拱式结构的特征及应用: 应用:门、窗、桥、巷道、窑洞 特征:杆轴是曲线,竖向荷载作用下有水平推力。和曲梁比较 三铰拱是由两条曲杆用铰相互联结,并各自与支座用铰相联结而成。 优点:在竖向荷载作用下拱存在水平推力作用,导致其所受的弯矩远比梁小,压力也比 较均匀;若合理选择拱轴,弯矩为 0,主要承受压力。 缺点:需要坚固而强大的地基基础来支承; 2、 拱的形式: 静定结构:三铰拱。 有两种形式:无拉杆三铰拱、有拉杆的三铰拱、及其变化形式、 做成折线即为三铰刚架 超静定结构:无铰拱、两铰拱 3、各部分名称: 跨度 L、 拱高:拱顶到两支承边线距离,f 拱脚铰、拱顶铰 对称拱、斜拱(不对称拱) f/l:矢跨比(高跨比)。高跨比对拱的主要性能有比较大的影响(1-1/10)。若 f→0, 三铰共线或接近共线,瞬变体系。 4、计算方法: 数解法、图解法 §4-2 三铰拱的数解法 竖向荷载作用下三铰平拱的支座反力和内力的计算公式,并和同跨同荷载的相应简 支梁比较。 一、 支座反力的计算: 三铰拱 三铰拱相当梁:

图示 R P2 v 对三较拱:∑M,=0乃=∑P0= ∑M,=0=∑= ∑X=0, H,=H。=H ∑M=0,H='以-Rl-a 结论:(1)三较拱的竖向反力与相当梁的竖向力相同: (2)水平推力仅与荷载及三个铰的位置有关,(即只与拱的矢跨比n有关,n十, H:fn↓,H↑)和拱轴形状无关。当荷载及跨度不变时,f↑,H↓,f+,H↑,f +0,H→∞,f0三拱共线瞬变体系。 (3)竖向向下荷载作用时推力为正,推力向内 2、内力的计算 任一横截面K:位置由坐标x、y及该处拱轴切线的倾角中确定。 取隔离体: ∑Mx=0,Mx=[Vx-Bx-a】-=Mg- >y=0.Q=V cos-P coso-Hsin o=O%coso-Hsn ∑X=0,N=Osin+Hcos 得出: MK=MK-HyK Qk=-中-Hsin中
图示 对三铰拱: 0 0, i i A B B P a M V V l = = = 0 0, i i B A A Pb M V V l = = = 0, X H H H = = = A B 1 1 1 1 ( ) 0, A C V l P l a M H f − − = = 结论:(1)三铰拱的竖向反力与相当梁的竖向力相同; (2)水平推力仅与荷载及三个铰的位置有关,(即只与拱的矢跨比 f/l 有关,f/l↑, H↓;f/l↓,H↑)和拱轴形状无关。当荷载及跨度不变时,f↑,H↓,f↓,H↑,f →0,H→∞,f=0 三拱共线瞬变体系。 (3)竖向向下荷载作用时推力为正,推力向内 2、内力的计算 任一横截面 K:位置由坐标 x、y 及该处拱轴切线的倾角φ确定。 取隔离体: M = M = V x − P (x − a )− Hy = M − Hy K K A K 0 1 1 0, 0, cos cos sin cos sin 0 1 ' Y = Q =VA − P − H = QK − H 0, sin cos ' 0 X = N == QK + H 得出: { MK=MK 0 -H•yK QK=QK 0cosψK- HsinψK

Nk=Qx0sin中x+Hcos中s 1}规定正负问题: 2)截面法求内力: 3)比较出公式适用范围(适用范围:竖向荷载(包括竖向均布荷载和集中力)作 用下的三铰平拱、带拉杆的拱)。 结论:(1)三铰撰的弯矩小于相当梁的弯矩; (2)N较大,Q较小 3、受力特点(比较法,由公式) 1)竖向荷载下,梁没有水平反力,拱则有水平推力,所以拱要求比梁更为坚固的 基础或支承结构。 2)由于水平推力的存在,三铰拱截面上的M比简支梁小,所以拱比梁能更有效地 发挥材料作用,适用于较大跨度或较重荷载。 3)在竖向荷载作用下,梁内无N,而拱内N较大,且一般为压力,所以拱可以用 抗压性能强而抗拉性能差的材料来建造,例如:砖、石、砼,便宜,造价低。 总之,拱比梁更适用于较大的跨度和较重的荷载。抗压更有利于抗压性能好的材料,但 三铰拱的基础比梁大:因此屋架中三铰拱常带拉杆,减少对墙或柱的推力。 4、拱内力图的绘制 曲线,沿拱轴逐点计算和描绘。 (1)沿拱轴将拱截成为若干相等的小段: (2)计算各截面处的y,tan,sin,cos (3)利用公式逐一计算各截面的M、Q、N值: (4)逐点描绘 理论上讲,只要用截面法求出拱截面的内力方程,就能作出内力图(内力图的特性 改变和梁、刚架不同),但由于拱轴线B曲线,一般为二次方程,则求出的内力方程为 高阶方程,且沿轴线作图比较困难。 因此通常用近似法作拱的内力图:用水平线代替拱轴线,用截面法求出一系列截面的内 力,在水平线上用描点法作出(按比例定位,用曲线板相连)。 微分关系复杂 区段叠加法不适用 也可采用叠加法绘制。 例4-1试绘制图4-9贴所示三较拱的内力图。三较供的拱轴为一匏物线,当坐标原 在左支座时,它的方程可由下式表达 y=新u-x) [解】先求支座反力,根据公式(4-4)、(4-5).(4-6)可得 R-P-10X10x920X10x6X3.105X10N=15N F,-F-10X10x3+20X10X6x9=15x10N=15
NK=QK 0 sinψK+ HcosψK 1}规定正负问题; 2}截面法求内力; 3)比较出公式适用范围(适用范围:竖向荷载(包括竖向均布荷载和集中力)作 用下的三铰平拱、带拉杆的拱)。 结论:(1)三铰拱的弯矩小于相当梁的弯矩; (2)N 较大,Q 较小 3、受力特点(比较法,由公式) 1)竖向荷载下,梁没有水平反力,拱则有水平推力,所以拱要求比梁更为坚固的 基础或支承结构。 2)由于水平推力的存在,三铰拱截面上的 M 比简支梁小,所以拱比梁能更有效地 发挥材料作用,适用于较大跨度或较重荷载。 3)在竖向荷载作用下,梁内无 N,而拱内 N 较大,且一般为压力,所以拱可以用 抗压性能强而抗拉性能差的材料来建造,例如:砖、石、砼,便宜,造价低。 总之,拱比梁更适用于较大的跨度和较重的荷载。抗压更有利于抗压性能好的材料,但 三铰拱的基础比梁大;因此屋架中三铰拱常带拉杆,减少对墙或柱的推力。 4、拱内力图的绘制 曲线,沿拱轴逐点计算和描绘。 (1) 沿拱轴将拱截成为若干相等的小段; (2) 计算各截面处的 y,tan,sin,cos (3) 利用公式逐一计算各截面的 M、Q、N 值; (4) 逐点描绘 理论上讲,只要用截面法求出拱截面的内力方程,就能作出内力图(内力图的特性 改变和梁、刚架不同),但由于拱轴线 B 曲线,一般为二次方程,则求出的内力方程为 高阶方程,且沿轴线作图比较困难。 因此通常用近似法作拱的内力图:用水平线代替拱轴线,用截面法求出一系列截面的内 力,在水平线上用描点法作出(按比例定位,用曲线板相连)。 微分关系复杂 区段叠加法不适用 也可采用叠加法绘制

o kN Ihriiiitinginn B×1.5m=12 M图(位kN:m 随4-9 F4-9.105x10×6:100X10X3=2.5×10N=2.5N 力求出后,即可根据式(4-7)、(4-8),(4-9)绘制其内力图。为此,将拱蔚分成八等分,然后 表4-1算出拱上各个燕面的M,Fa,Fw值,最后再根据表中所得数值绘得M,F。,F图,如 4-9cd所示 为了说明表4一1,现以离左支座的水平臣离为1.Sm处的截面1为例,计算其内力如下: 当x=1.5m时,由拱轴方程可求得 =41-z,=2-1.5)×1.5=1.75m m-竖=判1-20)-1-2x没)-可
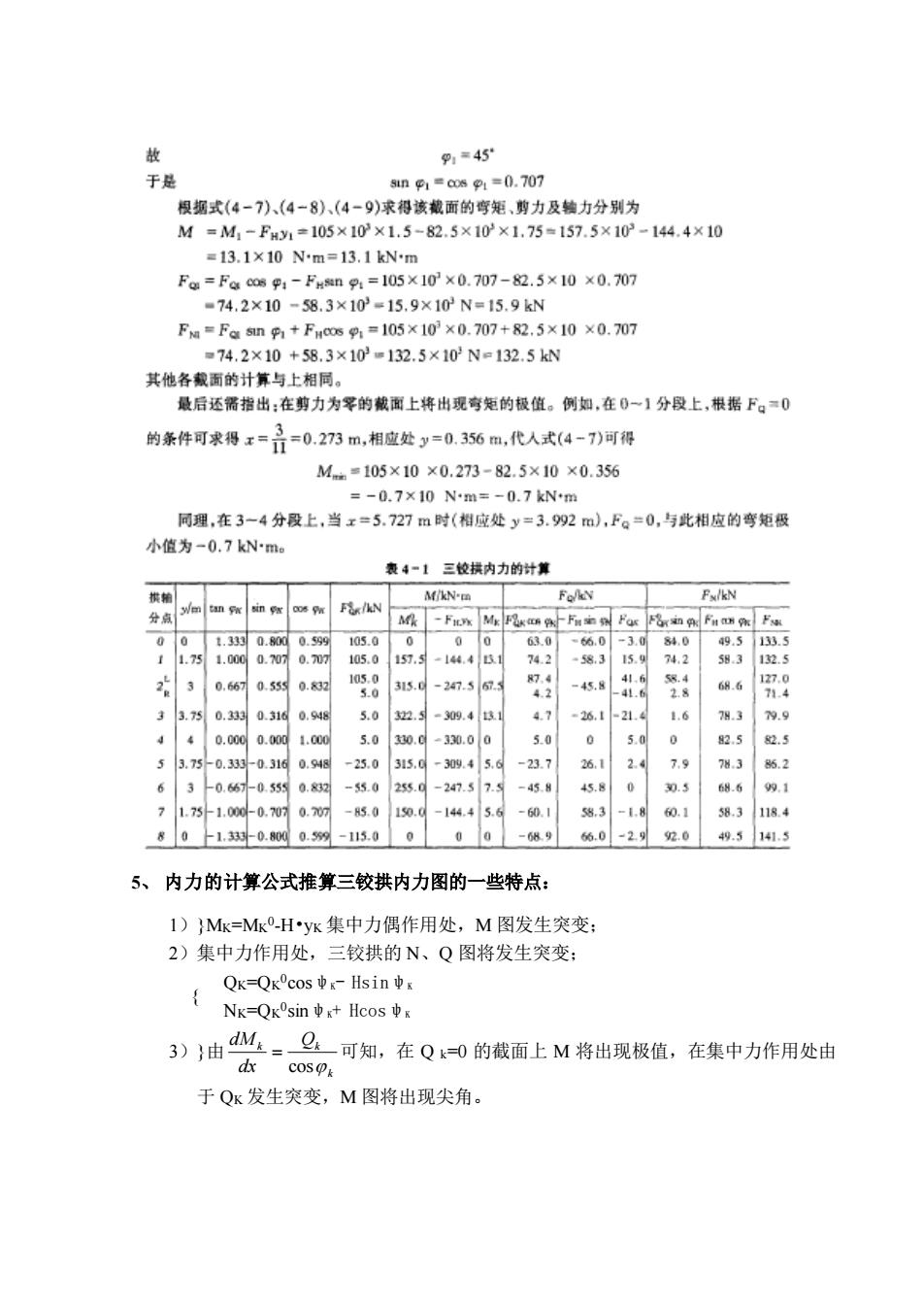
故 e.m45 于是 sn1=0=0.707 据式4-)、(4-8》.(4-9)求得该面的弯矩剪力及特力分别为 M=M1-F4y1=105×103×1.5-82.5×10×1.75=157.5×10-144.4×10 =13.1×10Nm=13.1kNm Fa=Fcc0s1-F4an=105×10×0.707-82.5×10×0.707 74.2×10-58.3×10=15.9×10N=15.9kN Fa=Fa5n1+Fs=105×102×0.70m+82.5×100.707 ■74.2×10+58.3×103m132.5×102N=132.5kN 其他各裁面的计算与上相同。 最后还需指出:在剪力为罗的搬面上将出现弯矩的极值。例如,在0一1分段上,根据F。=0 的条件可求得x==0.273m,相应处y=0.356m,代人式(4-7)可得 M==105×10×0.273-82.5×10×0.356 -0.7X10Nm= -0.7 kN'm 同理,在3-4分段上,当x=5.727m时(相应处y=3.92m),F。=0,与此相应的弯矩极 小值为-0.7kNm 表4-1三校拱内力的计算 M/kN'm 分 542 583 30.60.50.对 a50 -247.567 33.5 0.3330.31 .4 47 -26.121.4 79.5 0.00 5. 5.0 5.75外0.3 0.10.94 -2 24 63060.54.网 -55.0255.g-247.57. -45.8 45.8 0.5 68.6 71.751.000-0.00.70 -5.0150.d-144.45 -60.1 58.3 -1.80.1 58.3 1184 801.30.00.59-15.00 00 6的.0=2g2.04.5141.5 5、内力的计算公式推算三较拱内力图的一些特点: 1)Mk=Mk0HVK集中力偶作用处,M图发生突变: 2)集中力作用处,三较拱的N、Q图将发生突变: Nk=QKsin中w+Hcos中g )迪公Q可知,在Q0的被面上M将出现极值,在集中方作用处由 于QK发生突变,M图将出现尖角
5、 内力的计算公式推算三铰拱内力图的一些特点: 1)}MK=MK 0 -H•yK 集中力偶作用处,M 图发生突变; 2)集中力作用处,三铰拱的 N、Q 图将发生突变; { QK=QK 0cosψK- HsinψK NK=QK 0 sinψK+ HcosψK 3)}由 k k Qk dx dM cos = 可知,在 Q k=0 的截面上 M 将出现极值,在集中力作用处由 于 QK 发生突变,M 图将出现尖角

§4-3三铰拱的合理拱轴线 一、压力线 一般情况下,三铰拱任一截面上的内力有三个,这三个内力可以合成为一个合力(用图 表示),可以确定合力作用点,可能在截面上,也可能在截面的延伸面上。 实体三铰拱上每一截面上总压力在该截面(或其延伸面)上的作用点(合力的作用点的 连线)所连成的一条折线或曲线。 三铰拱的压力线可以用作图法作出,随荷载而变化,和荷载及三铰拱的三个铰位置有关 和拱的轴线形状无关。 己知压力线可以求出(完全确定)任一截面上的内力:力多边形和相应的压力多边形。 二、合理拱轴 当拱的轴线和压力线重合时,各截面形心到合力作用线的距离为0,则各截面上只有轴 向压力,正应力沿截面均匀分布,拱处于无弯矩状态,这时候材料的使用最经济,这样 的拱轴为合理拱轴。 在固定荷载下使拱处于无弯矩状态的轴线。对于竖向荷载作用下的三较平拱的合理拱 轴,可以用数解法求出拱合理拱轴的轴线方程。M0, =M/H 在竖向荷载作用下,三铰拱合力轴线纵坐标与简支梁弯矩成正比,与H成反比。 例4一2试求图4一10所示对称三校拱在沿全跨长的水平均布荷载g作用下的合理拱轴 线。 H 务理, 410 [解]作出相应简支梁如图4-10%所示,其弯矩方程为 M-Te(-x) 惟力F由式(4-6)求得为 放由式(4-10)得到拱的合理轴线方程为 ,-当- (4-1 由此可见,在沿全跨长的水平均布荷载作用下,三校拱的合理轴线是一根二次抛物线
§4-3 三铰拱的合理拱轴线 一、压力线 一般情况下,三铰拱任一截面上的内力有三个,这三个内力可以合成为一个合力(用图 表示),可以确定合力作用点,可能在截面上,也可能在截面的延伸面上。 实体三铰拱上每一截面上总压力在该截面(或其延伸面)上的作用点(合力的作用点的 连线)所连成的一条折线或曲线。 三铰拱的压力线可以用作图法作出,随荷载而变化,和荷载及三铰拱的三个铰位置有关。 和拱的轴线形状无关。 已知压力线可以求出(完全确定)任一截面上的内力:力多边形和相应的压力多边形。 二、合理拱轴 当拱的轴线和压力线重合时,各截面形心到合力作用线的距离为 0,则各截面上只有轴 向压力,正应力沿截面均匀分布,拱处于无弯矩状态,这时候材料的使用最经济,这样 的拱轴为合理拱轴。 在固定荷载下使拱处于无弯矩状态的轴线。对于竖向荷载作用下的三铰平拱的合理拱 轴,可以用数解法求出拱合理拱轴的轴线方程。M=0, 在竖向荷载作用下,三铰拱合力轴线纵坐标与简支梁弯矩成正比,与 H 成反比。 y M / H 0 =