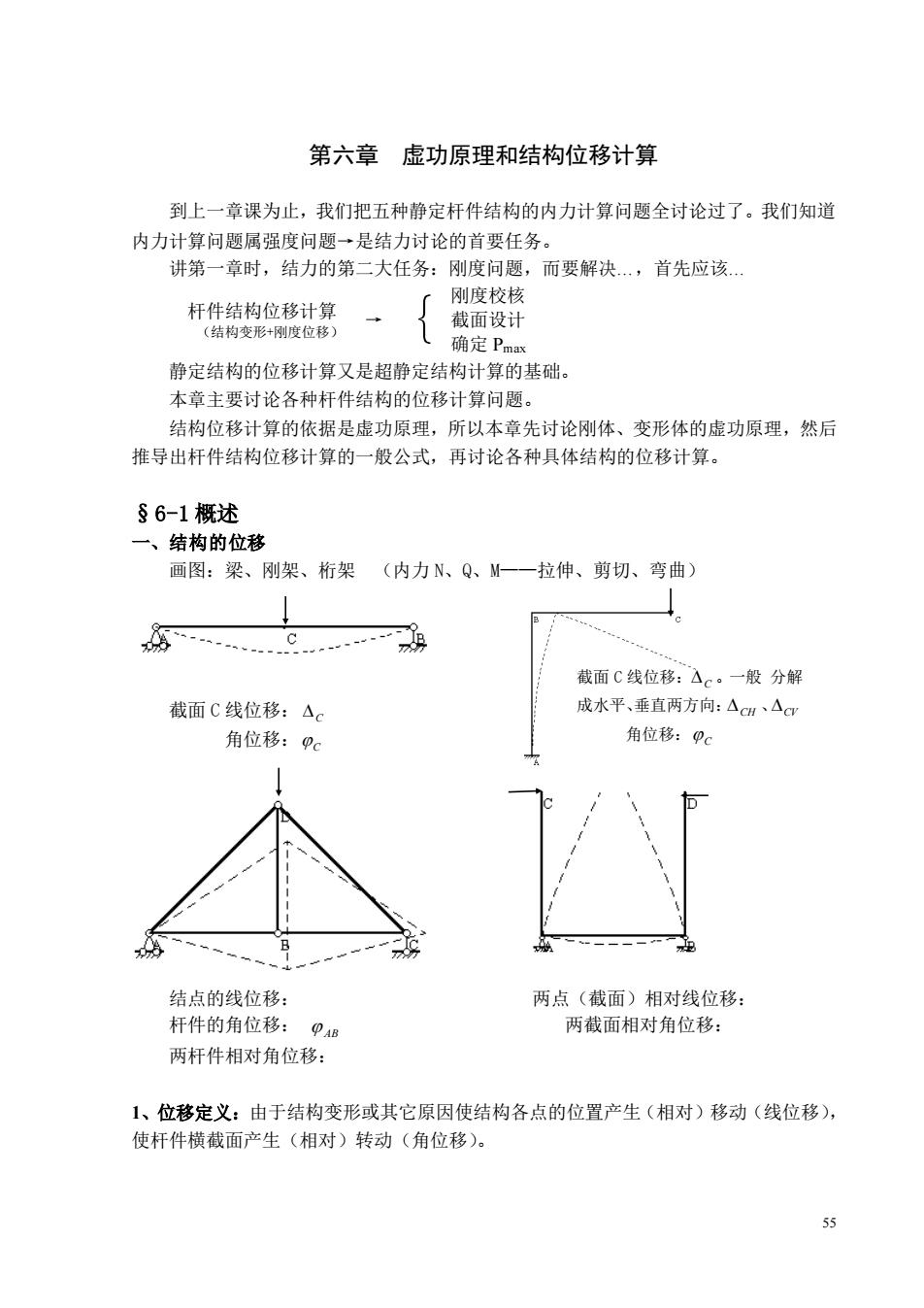
第六章虚功原理和结构位移计算 到上一章课为止,我们把五种静定杆件结构的内力计算问题全讨论过了。我们知道 内力计算问题属强度问题一是结力讨论的首要任务 讲第一章时,结力的第二大任务:刚度问题,而要解决.,首先应该 杆件结构位移计算 刚度校核 截面设计 (结构变形+刚度位移) 确定Pm, 静定结构的位移计算又是超静定结构计算的基础, 本章主要讨论各种杆件结构的位移计算问题。 结构位移计算的依据是虚功原理,所以本章先讨论刚体、变形体的虚功原理,然后 推导出杆件结构位移计算的一般公式,再讨论各种具体结构的位移计算。 §6-1概述 一、结构的位移 画图:梁、刚架、桁架(内力N、Q、M一一拉伸、剪切、弯曲) 截面C线位移:△。一般分解 截面C线位移:△c 成水平、垂直两方向:△gH△ 角位移:pc 角位移:pc 结点的线位移: 两点(截面)相对线位移: 杆件的角位移: AB 两截面相对角位移: 两杆件相对角位移: 1、位移定义:由于结构变形或其它原因使结构各点的位置产生(相对)移动(线位移), 使杆件横截面产生(相对)转动(角位移)
55 第六章 虚功原理和结构位移计算 到上一章课为止,我们把五种静定杆件结构的内力计算问题全讨论过了。我们知道 内力计算问题属强度问题→是结力讨论的首要任务。 讲第一章时,结力的第二大任务:刚度问题,而要解决.,首先应该. 杆件结构位移计算 (结构变形+刚度位移) → { 刚度校核 截面设计 确定 Pmax 静定结构的位移计算又是超静定结构计算的基础。 本章主要讨论各种杆件结构的位移计算问题。 结构位移计算的依据是虚功原理,所以本章先讨论刚体、变形体的虚功原理,然后 推导出杆件结构位移计算的一般公式,再讨论各种具体结构的位移计算。 §6-1 概述 一、结构的位移 画图:梁、刚架、桁架 (内力 N、Q、M——拉伸、剪切、弯曲) 截面 C 线位移: C 角位移: C 结点的线位移: 两点(截面)相对线位移: 杆件的角位移: AB 两截面相对角位移: 两杆件相对角位移: 1、位移定义:由于结构变形或其它原因使结构各点的位置产生(相对)移动(线位移), 使杆件横截面产生(相对)转动(角位移)。 截面 C 线位移: C 。一般 分解 成水平、垂直两方向: CH 、CV 角位移: C

2、位移的分类:6种 绝对位移:点(截面)线位移 一一分解成水平、垂直两方向 截面角位移: 杆件角位移: 相对位移:两点(截面)相对线位移一一沿连线方向 两截面相对角位移: 两杆件相对角位移: 统称为: 广义位移:角、线位移:相对、绝对位移 △ki:k:产生位移的方向:i:引起位移原因。如△A、△at、△A 广义力:集中力、力偶、分布荷载,也可以是上述各种力的综合 二、引起位移的原因 1、荷载作用:(荷载→内力→变形→位移) 2、温度改变:静定结构,温度改变,→0应力非0应变→结构变形 (材料胀缩引起的位移性质同) 3、支座移动:(无应力,无应变,但几何位置发生变化) 了刚体位移(制造误差同) (变形位移 三、计算位移的目的 1)刚度验算:最大挠度的限制 (框架结构弹性层间位移限值1450) 2)为超静定结构的弹性分析打下基础 3)预先知道变形后的位置,以便作出一定的施工措施: (起重机吊梁、板)(屋架安装)(建筑起拱)(屋窗、门、过梁)(结构要求高,精密) 四、计算位移的有关假定(简化计算) 1)弹性假设 2)小变形假设 建立平衡、应变与位移、位移与荷载成线性关系 3)理想约束(联结,不考虑阻力摩擦) 线性变形体系(线弹性体系) 形 荷载和位移呈线性关系,且荷载全撤除后位移将全部消 体 失,无残余变形,(可用位移叠加原理) 非线形变形体系 (分段线形叠加)》 4)位移叠加原理(类似内力、反力叠加)
56 2、位移的分类:6 种 绝对位移:点(截面)线位移——分解成水平、垂直两方向 截面角位移: 杆件角位移: 相对位移:两点(截面)相对线位移——沿连线方向 两截面相对角位移: 两杆件相对角位移: 统称为: 广义位移:角、线位移;相对、绝对位移 Δki:k:产生位移的方向;i:引起位移原因。如ΔAP、Δat、ΔAC 广义力:集中力、力偶、分布荷载,也可以是上述各种力的综合 二、引起位移的原因 1、荷载作用:(荷载→内力→变形→位移) 2、温度改变:静定结构,温度改变,→0 应力非 0 应变→结构变形 (材料胀缩引起的位移性质同) 3、支座移动;(无应力,无应变,但几何位置发生变化) { 刚体位移 (制造误差同) 变形位移 三、计算位移的目的 1)刚度验算:最大挠度的限制 (框架结构弹性层间位移限值 1/450) 2)为超静定结构的弹性分析打下基础 3)预先知道变形后的位置,以便作出一定的施工措施: (起重机吊梁、板)(屋架安装)(建筑起拱)(屋窗、门、过梁)(结构要求高,精密) 四、计算位移的有关假定 (简化计算) 1)弹性假设 2)小变形假设 建立平衡、应变与位移、位移与荷载成线性关系 3)理想约束(联结,不考虑阻力摩擦) 变 形 体 系 { 线性变形体系(线弹性体系) 荷载和位移呈线性关系,且荷载全撤除后位移将全部消 失,无残余变形,(可用位移叠加原理) 非线形变形体系 (分段线形叠加) 4)位移叠加原理(类似内力、反力叠加)

§6-2变形体系的虚功原理 位移 实位移:外因作用下结构实际位移 虚位移:根据解题需要,虚设位移状态(满足变形协调+边界条件) 统称为:广义位移 功: 力所做的功:该力大小乘以力方向上的相应位移 常力的功:T=PX△=PXD×cosa(大小、方向、作用点不变) 变力的功:T=∫dT=PXcos(P,ds)×ds 力偶所做的功: T=M· 功两要素:力与位移 P:广义力(力、力偶、相对力、相对力偶) △:和广义力相对应的广义位移(线、角、相对线、相对角) 注意:在定义功T时,没有说位移△是由力P引起的,可能由P或其它原因,但P 力照样作功。 例:简支梁,两个集中力,分别作用,先后作用。 2 △a P P:2 实功:W=1/2P,△n 实功:W=1/2P,△2 12 虚功:=P△ 可以看出:不论位移是否由内力引起,只要在力的作用方向上有位移,该力就对位移作 功。 引出功的形式有两种: 实功:力与位移相关。力在其本身引起的位移上所做的功。积分得:T=印×相对位移 /2,恒正 虚功:力与位移无关。力在由其它原因(别的力、温度变化.)引起的位移上所做 的功,T'=力×位移 注:①力:广义力:位移:广义位移 ②虚功并非不存在之意,力和位移是分别属于同一体系的两种彼此无关的状态,只强调 作功的力与位移彼此独立无关:做功的位移不是由力引起的,而是由其它因素(其它力、 其它外因)引起的 ③作虚功的位移,并不限于荷载引起的,也可以由其它原因引起的。 57
57 §6-2 变形体系的虚功原理 一、 位移 实位移:外因作用下结构实际位移 虚位移:根据解题需要,虚设位移状态 (满足变形协调+边界条件) 统称为:广义位移 二、 功: 力所做的功:该力大小乘以力方向上的相应位移 常力的功: T=P×Δ=P×D×cosa (大小、方向、作用点不变) 变力的功:T= s dT = s P×cos( P ,ds)×ds 力偶所做的功: T M= 功两要素:力与位移 P: 广义力(力、力偶、相对力、相对力偶) Δ:和广义力相对应的广义位移(线、角、相对线、相对角) 注意:在定义功 T 时,没有说位移Δ是由力 P 引起的,可能由 P 或其它原因,但 P 力照样作功。 例:简支梁,两个集中力,分别作用,先后作用。 可以看出:不论位移是否由内力引起,只要在力的作用方向上有位移,该力就对位移作 功。 引出功的形式有两种: 实功:力与位移相关。 力在其本身引起的位移上所做的功。积分得:T=P×相对位移 /2,恒正 虚功:力与位移无关。 力在由其它原因(别的力、温度变化.)引起的位移上所做 的功,T’=力×位移 注:①力:广义力;位移:广义位移 ②虚功并非不存在之意,力和位移是分别属于同一体系的两种彼此无关的状态,只强调 作功的力与位移彼此独立无关:做功的位移不是由力引起的,而是由其它因素(其它力、 其它外因)引起的 ③作虚功的位移,并不限于荷载引起的,也可以由其它原因引起的。 1 2 Δ11 Δ21 P1 1 2 Δ12 Δ22 P2 1 2 P1 P2 Δ11 Δ12 Δ21 Δ22 实功:W1=1/2P1Δ11 实功:W2=1/2P2Δ22 虚功:W=P1Δ12

④实功恒为正,虚功可正可负 ⑤两种功计算方法不同 本章讨论虚功原理,目的是为了研究结构的实际状态: 1)求结构未知力时:用虚位移 2)求结构未知位移时:用虚力 所以作虚功时,力状态和位移状态是彼此无关的,其中任一可以虚设,但并不是随 便假设。 所以对于虚功,应该强调两点: 1)假设的这种虚位移(或虚力)和所研究的实际力系(或实际位移)完全无关,可以 独立地按照我们的目的而虚设: 2)假设的虚位移(或虚力)在所研究的结构上应该是可能存在的位移(或力)状态: 也就是:位移状态:应该满足结构的变形协调条件,边界条件 力状态:应该满足结构的平衡条件。 1、广义力和广义位移对应(虚功的几种形式) 2、无关 关于虚功的几点说明 3、其他外因 4 一个实际 、一个虚设、解决两类问题 5、独立按求解目的假设 6、两足相应条件 三、刚体虚功原理(简单回顾一下) 对于某一刚体体系,存在一个力状态,满足静力平衡条件 同时存在一个位移状态,满足变形协调条件十边界条件 两种状态无关 ,对于力状态中所有外力对位移状态中对应的位移所做虚功总和为0。 注意:力状态、位移状态可以分别是虚设的,则:虚功原理有两种形式: 虚位移原理:求力 虚力原理:求位移 1、虚位移原理,求静定结构的约束力(支反力或内力)(结合例题) 步了取实际力状态,解除待求约束力的约束,用约束力代替,静定结构一可变 骤气沿待求约束力方向虚设单位位移,以刚体体系产生的位移状态 (刚体体系) 虚位移状态 ·虚功原理 单位位移法:在拟求未知力X方向虚设单位位移,利用几何关系求6,。 特点:利用几何方法求解静力平衡问题。 2、虚力原理,求刚体体系的位移(结合例题)
58 ④实功恒为正,虚功可正可负 ⑤两种功计算方法不同 本章讨论虚功原理,目的是为了研究结构的实际状态: 1)求结构未知力时:用虚位移 2)求结构未知位移时:用虚力 所以作虚功时,力状态和位移状态是彼此无关的,其中任一可以虚设,但并不是随 便假设。 所以对于虚功,应该强调两点: 1)假设的这种虚位移(或虚力)和所研究的实际力系(或实际位移)完全无关,可以 独立地按照我们的目的而虚设; 2)假设的虚位移(或虚力)在所研究的结构上应该是可能存在的位移(或力)状态; 也就是:位移状态:应该满足结构的变形协调条件,边界条件 力状态:应该满足结构的平衡条件。 关于虚功的几点说明 1、广义力和广义位移对应(虚功的几种形式) 2、无关 3、其他外因 4、一个实际、一个虚设、解决两类问题 5、独立按求解目的假设 6、满足相应条件 三、刚体虚功原理(简单回顾一下) 对于某一刚体体系,存在一个力状态,满足静力平衡条件 同时存在一个位移状态,满足变形协调条件+边界条件 两种状态无关 ,对于力状态中所有外力对位移状态中对应的位移所做虚功总和为 0。 注意:力状态、位移状态可以分别是虚设的,则:虚功原理有两种形式: 虚位移原理:求力 虚力原理:求位移 1、虚位移原理,求静定结构的约束力(支反力或内力)(结合例题) 步 骤 { 取实际力状态,解除待求约束力的约束,用约束力代替,静定结构→可变 (刚体体系) 沿待求约束力方向虚设单位位移,以刚体体系产生的位移状态 虚位移状态 →虚功原理 单位位移法:在拟求未知力 X 方向虚设单位位移,利用几何关系求δP 。 特点:利用几何方法求解静力平衡问题。 2、虚力原理,求刚体体系的位移(结合例题)

单位荷载法:在待求位移方向虚加一个单位荷载(两者对应,以达作虚功的目的) 特点:用静力平衡的方法来求解几何问题。推广到变形体的位移计算。 3、静定结构在支座移动时的位移计算(结合例题) 上面2的方法可以推广一下:从上节课的分析可知,静定结构在支座移动时,不产 生任何内力及变形,因此结构的位移纯属刚体位移,可以利用刚体体系的虚功方程求解。 例: 四、变形体体系的虚功原理 1、弯曲转角、轴向伸缩变形、横向剪切错动: 刚体体系的虚功原理不再适用,但可以将之推广: 由能量守恒:W+H=△EH:外部吸收的能量:W:外力所做的功 △E=T+UT:动能:U:变形能的增加(内力做功):E:结构能量的改变 若加载缓慢,不考虑能量损耗。 W=U外力所做的功=结构形变能的变化=内力所做的功 变形体体系上第I状态的外力沿第Ⅱ状态中相应的位移所作的虚功(外力虚功)= 变形体体系上第I状态的内力沿第Ⅱ状态中相应的变形(应变)所作的虚功(内力虚功)。 2、形变能:由于结构的材料发生变形而储存在结构内部的能量,等于加载过程中内力 所做的功: du rds 任一隔离体 轴向拉伸或压缩 剪切错动 弯曲变形 U=内力所做的功 对任一微段:du=∫Ndu+∫Ord+∫Mao 若各微段的变形连续分布:对一杆件u=∫Ndu+∫Or+Mg 对整个结构而言:U-∑∫Ndu+∑∫Qrds+∑「Mdg 3、虚功方程 ∑∫Pd△=∑∫Nd+∑∫Ord+∑[Mdo外力虚功=内力虚功 例:
59 单位荷载法:在待求位移方向虚加一个单位荷载(两者对应,以达作虚功的目的) 特点:用静力平衡的方法来求解几何问题。推广到变形体的位移计算。 3、静定结构在支座移动时的位移计算(结合例题) 上面 2 的方法可以推广一下:从上节课的分析可知,静定结构在支座移动时,不产 生任何内力及变形,因此结构的位移纯属刚体位移,可以利用刚体体系的虚功方程求解。 例: 四、变形体体系的虚功原理 1、弯曲转角、轴向伸缩变形、横向剪切错动: 刚体体系的虚功原理不再适用,但可以将之推广: 由能量守恒: W+H=E H:外部吸收的能量;W:外力所做的功 E=T+U T:动能;U:变形能的增加(内力做功);E:结构能量的改变 若加载缓慢,不考虑能量损耗: W=U 外力所做的功=结构形变能的变化=内力所做的功 变形体体系上第Ⅰ状态的外力沿第Ⅱ状态中相应的位移所作的虚功(外力虚功)= 变形体体系上第Ⅰ状态的内力沿第Ⅱ状态中相应的变形(应变)所作的虚功(内力虚功)。 2、形变能:由于结构的材料发生变形而储存在结构内部的能量,等于加载过程中内力 所做的功: 任一隔离体 轴向拉伸或压缩 剪切错动 弯曲变形 U=内力所做的功 对任一微段: du = Ndu + Qrds + Md 若各微段的变形连续分布:对一杆件 u = Ndu + Qrds + Md 对整个结构而言: U = Ndu + Qrds + Md 3、虚功方程 P.d = Ndu + Qrds + Md 外力虚功=内力虚功 例: du rds dψ

实际力状态:外力:P: 3 内力:N、Q、M满足平衡条件 实际位移状态:位移:△; 变形:du rdsdo 满足相容条件 虚位移状态:虚位移:汹 虚变形:u6n60 虚力状态:虚外力:P 虚内力:NQM可 虚位移原理:实际力状态+虚位移状态 ∑P8M=∑[Nu+「Q6n+「M6p) 虚力原理:实际位移状态+虚力状态 ∑p.△=∑[Ndu+[Ords+[Mdo 注 1 实 功能原理力与位移无关 力系平衡 一虚位移原理 虚功原理 位移相容 力原 也就是说: 作功的外力和内力组成力状态应满足平衡条件:位移和应变(变形)、位移状态应 满足变形协调条件和边界条件。这两种状态是彼此无关的,其中一个可以虚设,计算结 构位移时应取实际的位移状态,再虚设一种平衡的力状态进行求解(虚力原理)。 2)上式变形体体系的虚功原理适用于所有变形体体系(二维板壳结构和三维块体),我 们用于一维杆件结构的变形体体系的虚功原理。 3)实际的力状态或虚设的力状态(内外力)均应满足的静力平衡条件。 4)杆件结构的每一个杆件的位移状态(实际或虚设)均应满足:①任一微段满足应变~ 位移关系:②边界位移满足约束边界条件。 这两个条件即为变形协调条件,如果一个杆件的位移状态满足这两个条件,则称这 种状态能满足变形协调条件或称他是几何可能的位移状态。 60
60 实际力状态:外力:P; 内力:N、Q、M 满足平衡条件 实际位移状态:位移:Δ; 变形: du rds d 满足相容条件 虚位移状态:虚位移: 虚变形: u 虚力状态:虚外力: P 虚内力: N Q M Q 虚位移原理:实际力状态+虚位移状态 ( ) P. = Nu + Q + M 虚力原理:实际位移状态+虚力状态 ( ) P. = Ndu + Qrds + Md 注: 1) 也就是说: 作功的外力和内力组成力状态应满足平衡条件;位移和应变(变形)、位移状态应 满足变形协调条件和边界条件。这两种状态是彼此无关的,其中一个可以虚设,计算结 构位移时应取实际的位移状态,再虚设一种平衡的力状态进行求解(虚力原理)。 2)上式变形体体系的虚功原理适用于所有变形体体系(二维板壳结构和三维块体),我 们用于一维杆件结构的变形体体系的虚功原理。 3)实际的力状态或虚设的力状态(内外力)均应满足的静力平衡条件。 4)杆件结构的每一个杆件的位移状态(实际或虚设)均应满足:①任一微段满足应变~ 位移关系;②边界位移满足约束边界条件。 这两个条件即为变形协调条件,如果一个杆件的位移状态满足这两个条件,则称这 种状态能满足变形协调条件或称他是几何可能的位移状态。 功能原理 力与位移无关 虚功原理 力系平衡 位移相容 虚位移原理 虚力原理 实 实 虚 虚

§6-3位移计算的一般公式(单位荷载法) 一、基本公式的推导: 例:刚架在外荷载、支座位移及温度变化等作用下而发生变形→产生位移,要求:任 (2) 点K沿指定方向K-K的位移分量△a,实际位移状态5-14,C.实际的支座位移,。 Y、《,实际的轴向应变、剪切角、曲率。 仿照刚体体系求位移方法(单位荷载法):取实际的位移状态作为位移状态,虚设 一个力状态,越简单越好,且要求和△相对应,使虚功方程含△,要求对△,作虚功, 所以沿KK方向虚加一无量纲的单位荷载P=1(单位荷载法),则结构在虚单位荷载作 用下,支座C产生虚反力R,",产生内力N,Q,M组成一个平衡的力状态, 和原位移状态无关(虚)。例:5-14h) 外力虚功=P△x+RC,+R,C2+R,C,=1△x+∑RC 内力虚功=∑Ndu+「ordb+「Mdo) 由虚力原理建立虚力方程得: l.△x+∑Rc-∑Nda+[Ords+∫Mdo) 因此: △k=-∑Rc+∑gNdu+∫Mdp+∫ordb) 二、公式应用说明: 1、引起位移的外因可以是荷载,也可以是初应变、支座位移、温度变化、装配误差 制造误差、材料胀缩等。 2、引起位移的变形可以是弯曲变形,也可以是轴向变形或剪切变形,同时含刚体位移。 3、所能计算的位移可以是线位移,也可以是角位移或相对线(角)位移,也就是广义 位移。 4、杆件结构的类型可以是梁、刚架、桁架、拱或组合结构,它们可以是静定的,也可 以是超静定的。 61
61 §6-3 位移计算的一 般公式(单位荷载法) 一、基本公式的推导: 例:刚架在外荷载、支座位移及温度变化等作用下而发生变形→产生位移,要求:任一 点 K 沿指定方向 K-K 的位移分量Δka,实际位移状态 5-14a,Ca 实际的支座位移,εa、 γa、κa,实际的轴向应变、剪切角、曲率。 仿照刚体体系求位移方法(单位荷载法):取实际的位移状态作为位移状态,虚设 一个力状态,越简单越好,且要求和Δka相对应,使虚功方程含Δka,要求对Δka作虚功, 所以沿 K-K 方向虚加一无量纲的单位荷载 PK=1(单位荷载法),则结构在虚单位荷载作 用下,支座 C 产生虚反力 ' Rk , ' ' Rk ,产生内力 Nk ,Qk ,M k 组成一个平衡的力状态, 和原位移状态无关(虚)。例:5-14b) 外力虚功 = PK K + R1C1 + R2C2 + R3C3 =1.K +RC 内力虚功 ( ) = Ndu + Qrds + Md 由虚力原理建立虚力方程得: 1. K +RC ( ) = Ndu + Qrds + Md 因此: 二、公式应用说明: 1、引起位移的外因可以是荷载,也可以是初应变、支座位移、温度变化、装配误差、 制造误差、材料胀缩等。 2、引起位移的变形可以是弯曲变形,也可以是轴向变形或剪切变形,同时含刚体位移。 3、所能计算的位移可以是线位移,也可以是角位移或相对线(角)位移,也就是广义 位移。 4、杆件结构的类型可以是梁、刚架、桁架、拱或组合结构,它们可以是静定的,也可 以是超静定的。 = − RC + ( Ndu + Md + Qrds) k
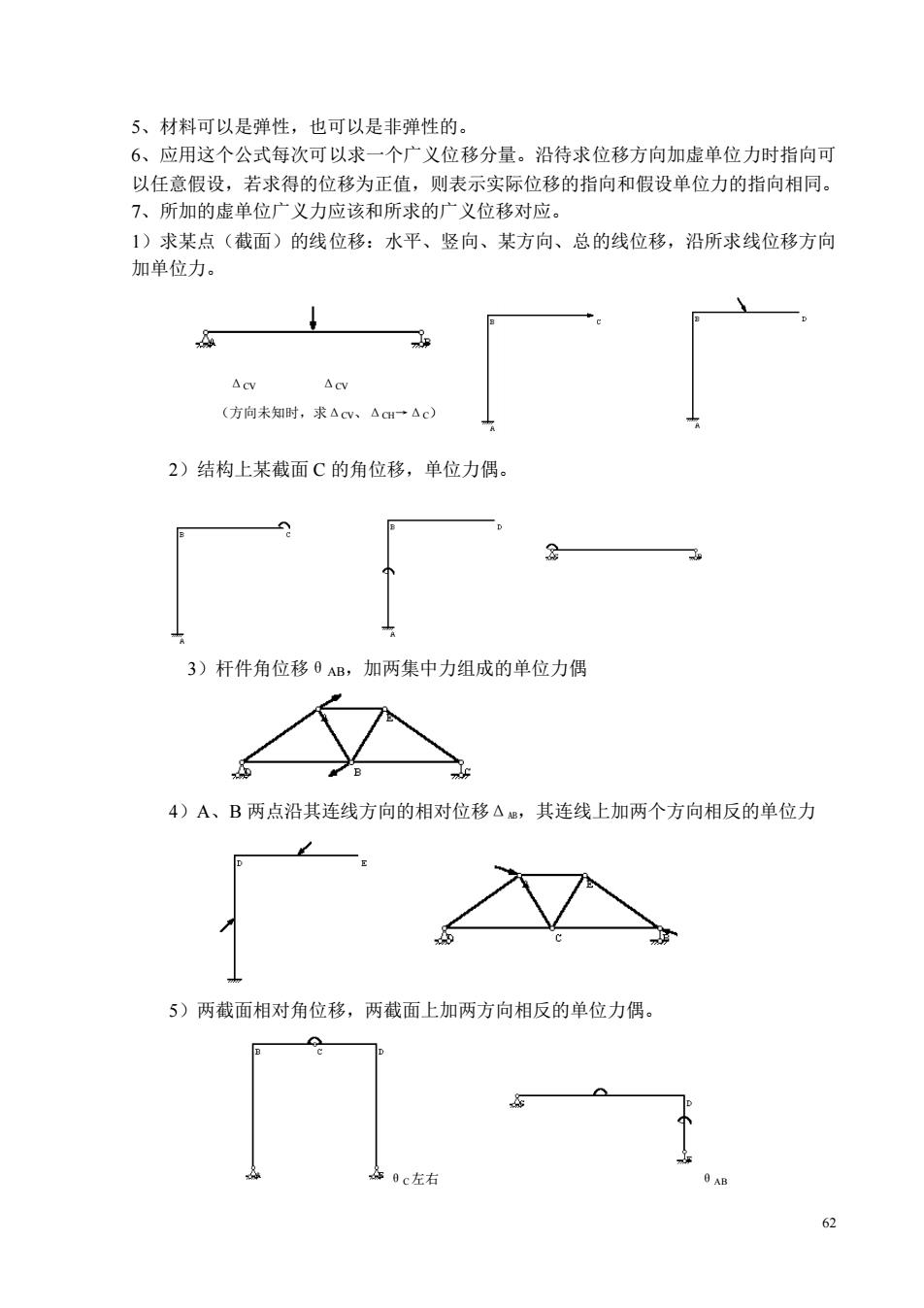
5、材料可以是弹性,也可以是非弹性的 6、应用这个公式每次可以求一个广义位移分量。沿待求位移方向加虚单位力时指向可 以任意假设,若求得的位移为正值,则表示实际位移的指向和假设单位力的指向相同。 7、所加的虚单位广义力应该和所求的广义位移对应。 1)求某点(截面)的线位移:水平、竖向、某方向、总的线位移,沿所求线位移方向 加单位力。 (方向未知时,求Acw、Aa一Ac) 2)结构上某截面C的角位移,单位力偶。 3)杆件角位移0AB,加两集中力组成的单位力偶 4)A、B两点沿其连线方向的相对位移△,其连线上加两个方向相反的单位力 5)两截面相对角位移,两截面上加两方向相反的单位力偶
62 5、材料可以是弹性,也可以是非弹性的。 6、应用这个公式每次可以求一个广义位移分量。沿待求位移方向加虚单位力时指向可 以任意假设,若求得的位移为正值,则表示实际位移的指向和假设单位力的指向相同。 7、所加的虚单位广义力应该和所求的广义位移对应。 1)求某点(截面)的线位移:水平、竖向、某方向、总的线位移,沿所求线位移方向 加单位力。 ΔCV ΔCV (方向未知时,求ΔCV、ΔCH→ΔC) 2)结构上某截面 C 的角位移,单位力偶。 3)杆件角位移θAB,加两集中力组成的单位力偶 4)A、B 两点沿其连线方向的相对位移ΔAB,其连线上加两个方向相反的单位力 5)两截面相对角位移,两截面上加两方向相反的单位力偶。 θC左右 θAB

6)两杆件的相对角位移 两个方向相反的单位力偶如图,每个单位力偶由两个集中力形成。 前述广义位移主要有六种形式,相应的广义力也有六种,两者一致。 §6-4静定结构在荷载作用下的位移计算 一、一般公式 △s=-∑Rc+∑JNdu+∫Mdo+∫ords) 若引起位移的外因仅是荷载,即仅考虑荷载作用: 1)支座位移C=0,也无温度影响: 2)微段变形du,rds,dp是由实际荷载在ds微段引起的轴向、剪切和弯曲变形,记为: d山r,rds,dpp。设Np、Qp、Mp分别表示实际荷载作用下结构内微段的轴力、剪力、 弯矩。 对于线弹性材料,由材料力学公式知: dur Nods ,d=kgd」 GA doe Mods 注:①杆件的拉伸刚度 剪切刚度 弯曲刚度 ②1一舅应为沿酸面分布不均匀的修正系数。和面形状有关。 矩形截面:k=12 圆形截面:k=10/9 (工字形截面:k=AA,A1(腹板面积) 薄壁圆环形截面:k=2 3)代入位移公式,得由荷载引起: △w=∑Ndup+∑∫Mdpn+∑∫or,d 这就是平面杆件结构在荷载作用下的位移计算公式。 单位荷载法:沿所求位移方向虚设单位荷载P=1求所求结构位移的方法 二、 公式说明
63 6)两杆件的相对角位移 两个方向相反的单位力偶如图,每个单位力偶由两个集中力形成。 前述广义位移主要有六种形式,相应的广义力也有六种,两者一致。 §6-4 静定结构在荷载作用下的位移计算 一、一般公式 = − RC + ( Ndu + Md + Qrds) k 若引起位移的外因仅是荷载,即仅考虑荷载作用: 1)支座位移 C =0,也无温度影响; 2)微段变形 du,rds,d 是由实际荷载在 ds 微段引起的轴向、剪切和弯曲变形,记为: duP,rPds,d P 。设 NP、QP、MP 分别表示实际荷载作用下结构内微段的轴力、剪力、 弯矩。 对于线弹性材料,由材料力学公式知: EA N ds du P P = , GA Q ds ds k P P = , EI M ds d P P = 注:①杆件的拉伸刚度 剪切刚度 弯曲刚度 ② * 2 2 2 dA b S I A k A = ——剪应力沿截面分布不均匀的修正系数,和截面形状有关。 { 矩形截面:k=1.2 圆形截面:k=10/9 工字形截面:k=A/A1,A1(腹板面积) 薄壁圆环形截面:k=2 3)代入位移公式,得由荷载引起: = Ndu + Md + Qr ds P P kP P = + + ) . ( ds EI MM ds GA kQQ ds EA N NP p P kp 这就是平面杆件结构在荷载作用下的位移计算公式。 单位荷载法:沿所求位移方向虚设单位荷载 P = 1 求所求结构位移的方法 二、 公式说明

1、下、M、互:P=1引起的内力对于静定结构均可由平衡条件求解 N。、Mp、Qp:实际荷载引起的内力。两组内力符号规定一致 2、EA、EI、GA:抗拉、抗弯、抗剪刚度。位移与截面有关 3、∫:杆件长度积分:∑:各杆件和积分值求和一一积分法 建立内力函数时,实际状态与虚拟状态的坐标应取为一致。 4、对于不同类型的结构,上式可以简化: 1)梁、刚架:以弯曲变形为主,轴向、剪切变形很小,可以略去。(结合例题说明) A=∑jWMk EI 6-2试求图6-16所示简支梁(E团=常数,GA=常数)中点C的竖向位移A和酸西 B的 解】(1)求4a 速拟状如围6-16所示。设以A为坐标氟点,则当0 10.2% 这表男,对于深果,剪切变形对位移的影响不可忽视。 2)求 6-16c所示,M和M,的方程如下: M=-平,M,=(红-2) 代入式(6-10)得 %-自(红-)d=台(1) 计算结果为负,表示实际位移与所设虚家荷载的方向相反,即复图B的转角不是顺时针方向而 是反时针方向(实际方向如圆括号内箭头所示)
64 1、 N 、 M 、Q : P = 1 引起的内力 对于静定结构均可由平衡条件求解 NP、 MP 、QP :实际荷载引起的内力。两组内力符号规定一致 2、EA、EI、GA:抗拉、抗弯、抗剪刚度。位移与截面有关 3、 :杆件长度积分; :各杆件和积分值求和——积分法 建立内力函数时,实际状态与虚拟状态的坐标应取为一致。 4、对于不同类型的结构,上式可以简化: 1)梁、刚架:以弯曲变形为主,轴向、剪切变形很小,可以略去。(结合例题说明) = ds EI MM P kp