第五章静定平面桁架 一、基本橱念 静定桁架的计算简图是由多根直杆两端用较连接而成的几何不变无多余约束体系。同梁 和刚架相比,桁架各杆只有轴力,截面上的应力分布均匀,可以充分发挥材料的作用,是大 跨度结构常用的一种形式。 静定桁架内力计算方法有:结点法,取结点为隔离体,每个结点有两个平衡方程:截面 法,取架的一部分为隔离体,每次可列三个方程。 组合结构由二力杆和梁式杆组成,要正确区分两类杆件。一般先计算二力杆的轴力,然 后再计算梁式杆的弯矩、剪力和轴力。 二、部分题解 5558试指出桁架中内力为零的杆。 解:5-55-8桁架中内力为零的杆用红色标注:分别为12根、6根、14根、13根
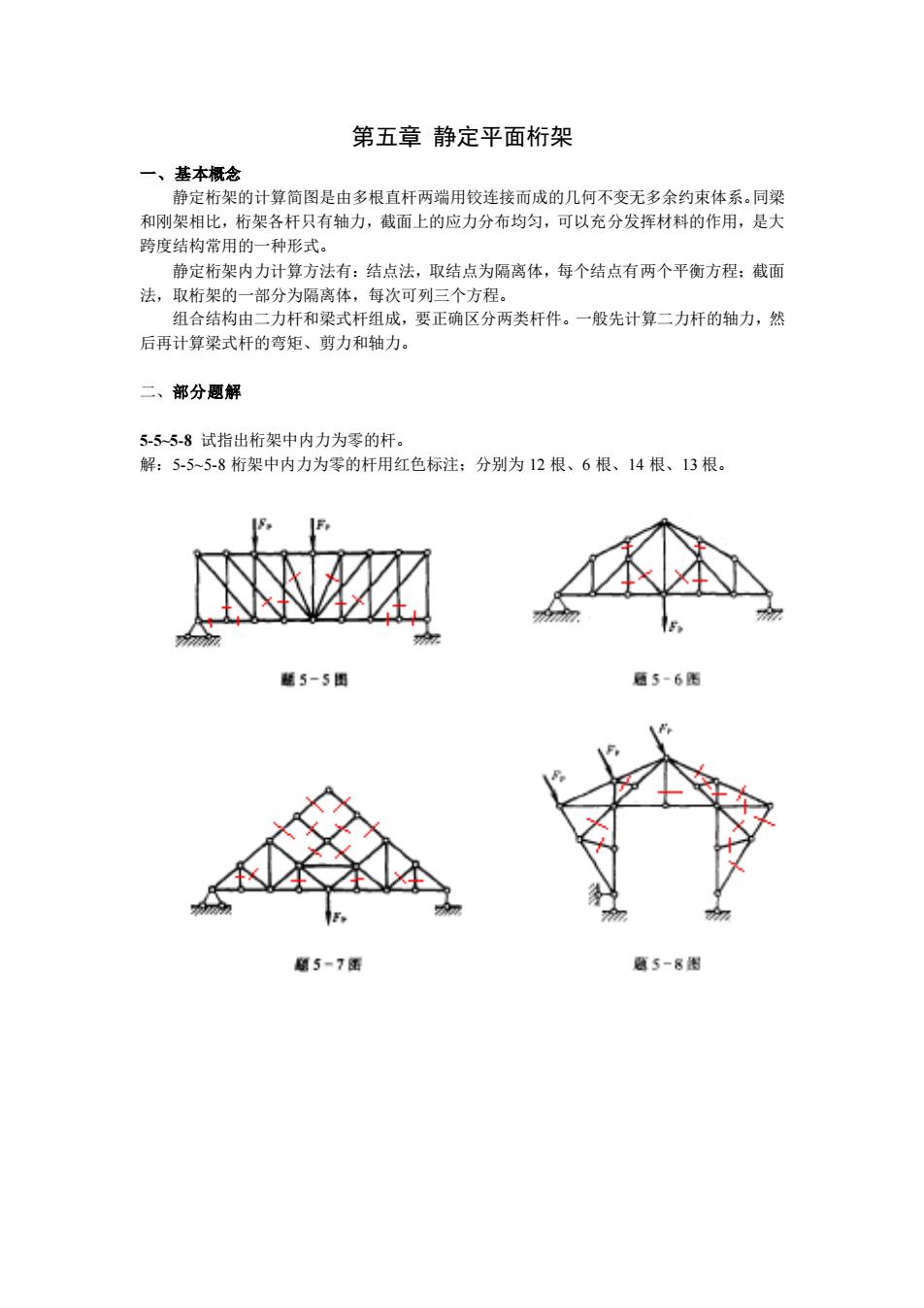
第五章 静定平面桁架 一、基本概念 静定桁架的计算简图是由多根直杆两端用铰连接而成的几何不变无多余约束体系。同梁 和刚架相比,桁架各杆只有轴力,截面上的应力分布均匀,可以充分发挥材料的作用,是大 跨度结构常用的一种形式。 静定桁架内力计算方法有:结点法,取结点为隔离体,每个结点有两个平衡方程;截面 法,取桁架的一部分为隔离体,每次可列三个方程。 组合结构由二力杆和梁式杆组成,要正确区分两类杆件。一般先计算二力杆的轴力,然 后再计算梁式杆的弯矩、剪力和轴力。 二、部分题解 5-5~5-8 试指出桁架中内力为零的杆。 解:5-5~5-8 桁架中内力为零的杆用红色标注;分别为 12 根、6 根、14 根、13 根
5一10求图示桁架中a、b杆件的内力 解:()求N。:用截面1一I截取上方为隔离体,由∑X=0可得N。=√2P (2)求N。:结点1为K结点,故有N。=-N。=-√2P: 再由结点2的平衡条件∑X=0可得N。=-P 1 4m2m 4m 3m 5一12求图示桁架中a、b、c三根杆件的内力 解:先由∑M=0求出B支座反力 Fp=30kN 取图示截面以右为隔离体 由∑M=0有F*4-30*3=0 得F=22.5kN 3m 再由∑M。=0 有22.5*8+F*4=0得F=-45k 取D结点为隔离体,由∑F=O可知ED、BD两杆的内力相等, 又由∑Fx=0得2Fe+F=0 Fye=22.5kN R2号5=75w
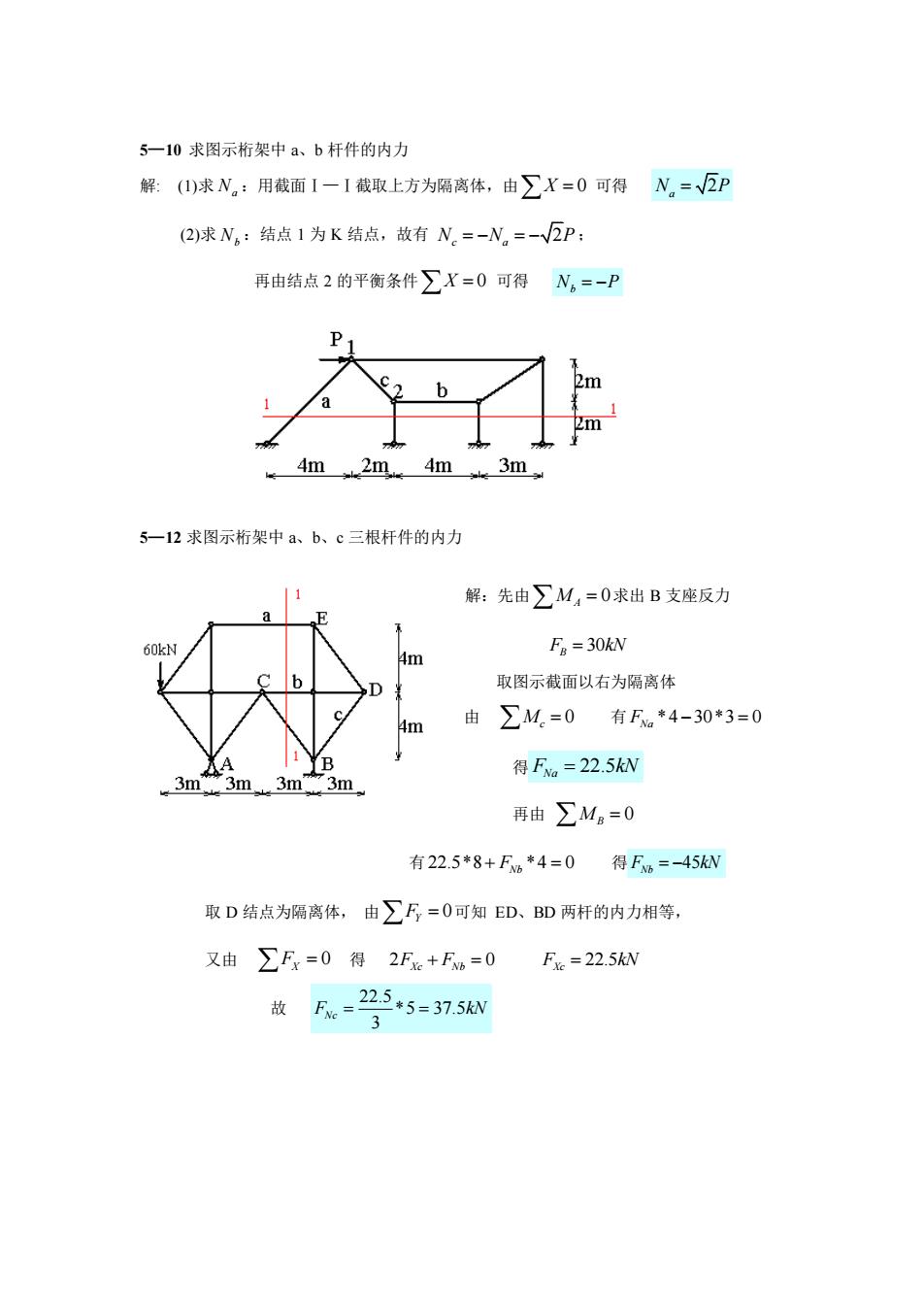
5—10 求图示桁架中 a、b 杆件的内力 解: (1)求 Na :用截面Ⅰ—Ⅰ截取上方为隔离体,由 X = 0 可得 2 N P a = (2)求 Nb :结点 1 为 K 结点,故有 2 N N P c a = − = − ; 再由结点 2 的平衡条件 X = 0 可得 N P b = − 5—12 求图示桁架中 a、b、c 三根杆件的内力 解:先由 0 MA = 求出 B 支座反力 30 F kN B = 取图示截面以右为隔离体 由 0 M c = 有 *4 30*3 0 FNa − = 得 22.5 F kN Na = 再由 0 MB = 有 22.5*8 *4 0 + = FNb 得 45 F kN Nb = − 取 D 结点为隔离体, 由 0 FY = 可知 ED、BD 两杆的内力相等, 又由 0 FX = 得 2 0 F F Xc Nb + = 22.5 F kN Xc = 故 22.5 *5 37.5 3 F kN Nc = =

5-14求图示桁架中a、b、c、的四根杆件的内力 解:就ABCK部分来看是对称的,但其所承受的荷载是 反对称的。所以ABCK部分的内力应属反对称的,而 KB杆位于对称轴上,故其内力必为零。 既有F=0 并且因AK与CK处于对称位置,故应有F=-F 由结点K的平衡条件∑F=0 kd d 有-方+方+P=0@ 将=-带入上式即 -方-方+P=0 &r-9e -9 人-9 516求图示桁架中a杆的内力 解:(1)求支反力'4='a=15kW (2)判断零杆见图中红色标注 16 15 (3)取截面1-1以右 ∑Me=0 Nm×3-15×2=0 照5=16图 N.=10 N。=5N5W
5—14 求图示桁架中 a、b、c、的四根杆件的内力 解:就 ABCK 部分来看是对称的,但其所承受的荷载是 反对称的。所以 ABCK 部分的内力应属反对称的,而 KB 杆位于对称轴上,故其内力必为零。 既有 0 FNa = 并且因 AK 与 CK 处于对称位置,故应有 F F Nc Nd = − 由结点 K 的平衡条件 0 FX = 有 1 1 0 2 2 − + + = F F P Nd Nc (a) 将 F F Nc Nd = − 带入上式 即 1 1 0 2 2 − − + = F F P Nd Nd ∴ 2 2 F P Nd = 2 2 F F P Nc Nd = − = − 2 2 F F P Nb Nc = − = 5-16 求图示桁架中 a 杆的内力 解:(1)求支反力 15 V V kN A B = = (2)判断零杆见图中红色标注 (3)取截面 1-1 以右 0 MC = 3 15 2 0 Nax − = 10 Nax = 5 5 N kN a = P a c b A B C K d d d d d

5一24试计算图示组合结构内力 40kN 60kN 80kN 解:由∑M4=0 得Fy=100kN: D E 由∑MB=0 得FAy=8OkW G 取图示截面以右部分为隔离体, om 由∑M.=0得Fax=40kW B 1 4*3=12m 由∑F=0有 5 FcH-80+100=0 故Fcm=-20N2kW 由2F=0有-5a+方205-40=0故5a=20y 依次取结点H、I、C、G、E为隔离体,可求出各链杆的轴力:Fm=20kN、Fw=80kN、 Fx=-141.42W、Fm=-20kW、Fxec=0kW、Fcc=-56.57kW、FGE=40kW、 FGF=-40kN、FEF=-113.14kN、FED=80kN。 取梁式杆AD为隔离体:ME4=40*6=240kWm(外侧受拉) 取梁式杆AD为隔离体:MkB=40*6=240kVm(外侧受拉)
5—24 试计算图示组合结构内力 解:由 0 MA = 得 100 F kN BY = ; 由 0 MB = 得 80 F kN AY = 取图示截面以右部分为隔离体, 由 0 M c = 得 40 F kN BX = 由 0 FY = 有 1 80 100 0 2 FNCH − + = 故 20 2 F kN NCH = − 由 0 FX = 有 1 *20 2 40 0 2 − + − = FNCI 故 20 F kN NCI = 依次取结点 H、I、C、G、E 为隔离体,可求出各链杆的轴力: 20 F kN NIH = 、 80 F kN NIJ = 、 141.42 F kN NIK = − 、 20 F kN NHK = − 、 0 F kN NEC = 、 56.57 F kN NGC = − 、 40 F kN NGE = 、 40 F kN NGF = − 、 113.14 F kN NEF = − 、 80 F kN NED = 。 取梁式杆 AD 为隔离体: 40*6 240 M kN m FA = = (外侧受拉) 取梁式杆 AD 为隔离体: 40*6 240 M kN m KB = = (外侧受拉) 40kN 60kN 80kN A B C F G H K D E I J 4*3=12m 6m 3m