
第十一章动载荷 ⊙嘉直人善
第十一章 动载荷

第十一章动载荷 §11-1动载荷概念和工程实例 §11-2惯性力问题 §11-3构件受冲击时的应力及强度计算 §11-4提高构件抵抗冲击能力的措施 §11-5构件的动力强度和冲击韧度 ⊙嘉面大婆
第十一章 动载荷 §11-1 动载荷概念和工程实例 §11-2 惯性力问题 §11-3 构件受冲击时的应力及强度计算 §11-4 提高构件抵抗冲击能力的措施 §11-5 构件的动力强度和冲击韧度

第十一章动载荷 §11一1动载荷概念和工程实例 一、静荷载的概念: 载荷不随时间变化(或变化极其平稳缓慢)且使 构件各部件加速度保持为零(或可忽略不计),此类 载荷为静载荷。 二、动载荷的概念: 载荷随时间急剧变化且使构件的速度有显著变化 (系统产生惯性力),此类载荷为动载荷。 例:起重机以等速度吊起重物,重物对吊索的作用为静载。 起重机以加速度吊起重物,重物对吊索的作用为动载。 旋转的飞轮、气锤的锤杆工作时、打桩均为动荷载作用。 ⊙嘉道人
§11—1 动载荷概念和工程实例 一、静荷载的概念: 二、动载荷的概念: 例:起重机以等速度吊起重物,重物对吊索的作用为静载。 起重机以加速度吊起重物,重物对吊索的作用为动载。 旋转的飞轮、气锤的锤杆工作时、打桩均为动荷载作用。 载荷不随时间变化(或变化极其平稳缓慢)且使 构件各部件加速度保持为零(或可忽略不计),此类 载荷为静载荷。 载荷随时间急剧变化且使构件的速度有显著变化 (系统产生惯性力),此类载荷为动载荷。 第十一章 动载荷

第十一章动载着 三、动响应: 构件在动载荷作用下产生的各种响应(如应力、应变、位 移等),称为动响应。 实验表明:在静载荷下服从虎克定律的材料,只要应力不超 过比例极限,在动载荷下虎克定律仍成立且E静=E动。 四、动载荷问题的分类: (1)构件作等加速直线运动和等速转动时的动应力计算; (2)构件在受冲击和作强迫振动时的动应力计算; (3)构件在交变应力作用下的疲劳破坏和疲劳强度计算。 ⊙嘉大婆
(1)构件作等加速直线运动和等速转动时的动应力计算; (2)构件在受冲击和作强迫振动时的动应力计算; (3)构件在交变应力作用下的疲劳破坏和疲劳强度计算。 构件在动载荷作用下产生的各种响应(如应力、应变、位 移等),称为动响应。 实验表明:在静载荷下服从虎克定律的材料,只要应力不超 过比例极限,在动载荷下虎克定律仍成立且 E静 = E动。 三、动响应: 四、动载荷问题的分类: 第十一章 动载荷
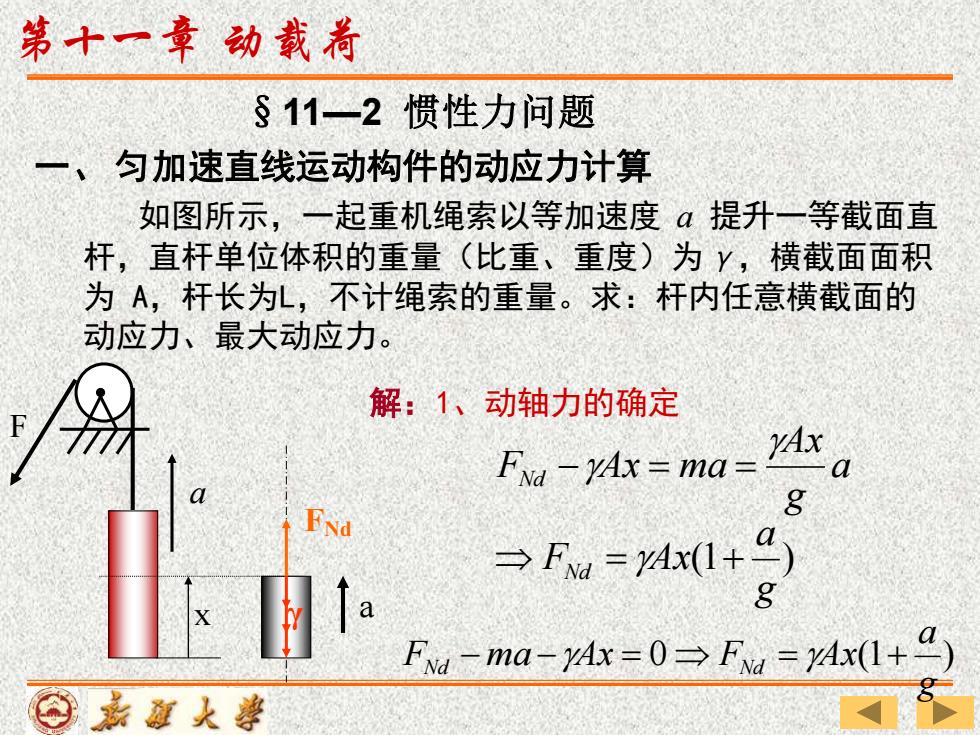
第十一章动载荷 §11一2惯性力问题 一、匀加速直线运动构件的动应力计算 如图所示,一起重机绳索以等加速度α提升一等截面直 杆,直杆单位体积的重量(比重、重度)为Y,横截面面积 为A,杆长为,不计绳索的重量。求:杆内任意横截面的 动应力、最大动应力。 解:1、动轴力的确定 FNd-yAx ma= 8 →FM=Ax1+a) a FNd-ma-rAx=0 Fvd yAx(1+9) ⊙嘉道火善
§11—2 惯性力问题 一、 匀加速直线运动构件的动应力计算 F a 如图所示,一起重机绳索以等加速度 a 提升一等截面直 杆,直杆单位体积的重量(比重、重度)为γ,横截面面积 为 A,杆长为L,不计绳索的重量。求:杆内任意横截面的 动应力、最大动应力。 解:1、动轴力的确定 x γ FNd a (1 ) g a F Ax a g Ax F Ax ma Nd Nd = + − = = 0 (1 ) g a F ma Ax F Ax Nd − − = Nd = + 第十一章 动载荷

第十一章动载荷 2、动应力的计算 yAx(1+ A 8=yx1+ 8 3、最大动应力 x=L→oam=yLl+ 8 a=0时 od-Yx-0 04=0n1+4 K,=1+C)→o1=K0 8 K一动荷系数:下标s 受静荷载作用: 下标d一受动荷载作用。 FNd -KaFN:Od-Kao ALd=KaAL 4、强度计算 ona≤[o] ⊙嘉题火尊
2、动应力的计算 (1 ) (1 ) g a x A g a Ax A FNd d = + + = = 3、最大动应力 (1 ) max g a x = L d = L + a = 0时 (1 ) g a x d st d st = + = = d d Kd st g a K = (1+ ) = Kd——动荷系数;下标 st——受静荷载作用; 下标d——受动荷载作用。 FNd = Kd FNj d = Kd j Ld = Kd Lj ; ; 4、强度计算 d max d 第十一章 动载荷

第十一章动载荷 二、构件作等速转动时的动应力 一薄壁圆环平均直径为D,壁厚为t, 以等角速度ω绕垂直于环平面且过圆心的 平面转动,圆环的比重为Y。求圆环横截 面的动应力。 解:1、求动轴力 0a=o2R=02 2 F=ma, 8 (2)9= ma,ALmu,Ay D gL 8 ⊙嘉道人善
二、构件作等速转动时的动应力 D ω 一薄壁圆环平均直径为 D,壁厚为 t, 以等角速度 ω绕垂直于环平面且过圆心的 平面转动,圆环的比重为 γ。求圆环横截 面的动应力。 qd 解:1、求动轴力 2 2 (1) 2 2 2 D g AL F ma D a R n n = = = = 2 (2) 2 D g A gL AL a L ma q n n d = = = 第十一章 动载荷

第十一章动载着 6)y=0→2ra-3d,sm0-9D dφ →人e9D-4mD 4g 2、动应力的计算 Nd Nd -00-成= o114g8 ⊙嘉大兽
FNd FNd φ d φ g A D F q D d q q D D Y F Nd d Nd d d 2 4 1 sin 2 (3) 0 2 2 2 0 = = = → = = 2、动应力的计算 ) 2 ; ( 4 2 2 2 D v R g v g D A FNd d = = = = = 第十一章 动载荷

第十一章动载荷 §11一3构件受冲击荷载作用时的动应力 一、冲击 一个运动的物体(冲击物)以一定的速度,撞击另 一个静止的物体(被冲击构件),静止的物体在瞬间使 运动物体停止运动,这种现象叫做冲击。 二、冲击问题的分析方法:能量法 假设 1、被冲击构件在冲击荷载的作用下服从虎克定律; 2、不考虑被冲击构件内应力波的传播 3、冲击过程只有动能、势能、变形能的转换,无其它能量损失。 4、冲击物为刚体,被冲击构件的质量忽略不计; ⊙嘉道火兽
§11—3 构件受冲击荷载作用时的动应力 一、冲 击 一个运动的物体(冲击物)以一定的速度,撞击另 一个静止的物体(被冲击构件),静止的物体在瞬间使 运动物体停止运动,这种现象叫做冲击。 二、冲击问题的分析方法:能量法 假设—— 1、被冲击构件在冲击荷载的作用下服从虎克定律; 2、不考虑被冲击构件内应力波的传播 3、冲击过程只有动能、势能、变形能的转换,无其它能量损失。 4、冲击物为刚体,被冲击构件的质量忽略不计; 第十一章 动载荷

第十一章动载荷 三、冲击问题的简便计算方法 1、自由落体冲击 如图所示,L,A,E,Q,h均为已知量, 求:杆所受的冲击应力。 解(1)冲击物的机械能: T+V=0+Qh+△a) F A (2)被冲击物的动应变能 A △为被冲击物的最大变形量,F为冲击载荷 (3)能量守恒( EA Aa) EA →Fa= ⊙嘉题大事
Q h L 1、自由落体冲击 Δd Fd 如图所示,L、A、E、Q、h 均为已知量, 求:杆所受的冲击应力。 解(1)冲击物的机械能: 0 ( ) T +V = +Q h + d (2)被冲击物的动应变能 Ud = Fd d 2 1 (3)能量守恒 ( ) 2 1 2 1 ( ) 2 d d d d d d d d L EA F EA F L L EA Q h F = → = + = = 三、冲击问题的简便计算方法 d为被冲击物的最大变形量,Fd为冲击载荷 第十一章 动载荷