
应力、应变状态分析 典型习题解析 1己知矩形截面梁,某截面上的剪力F=120kN及弯矩M=10kN·m。绘出表示1、2、3及4 点应力状态的微体,并求出各点的主应力。b=60mm,h=100mm。 10kN-m 配 了 4 Fs=120 kN 题1图 解题分析:从图中可分析1、4点是单向应力状态,2点在中性轴上为纯剪切应力状态,3 点微体上既有正应力又有切应力。 解:1、画各点处微体的应力状态图 取平行和垂直与梁横截面的六个平面,构成微体。则各点处的应力状态如图示。 2、计算各点处主应力 哭载面惯性矩为上-管-00000n:0410a 12 1点处弯曲正应力(压应力) 500×10m1 1点为单向压缩受力状态,所以o1=o2=0,0,=-100MPa 2点为纯剪切应力状态, 3x120x103N 72x601001Dm=30x10=30NMm(向下) 容易得到,o1=30MPa,c2=0,a3=-30MPa 3点为一般平面应力状态 弯正应力a=5_10x10N:mx25x10'm-50×10a=50MPa 500x10m 弯曲切应力
应力、应变状态分析 典型习题解析 1 已知矩形截面梁,某截面上的剪力FS=120 kN及弯矩 M = 10kN ⋅ m 。绘出表示 1、2、3 及 4 点应力状态的微体,并求出各点的主应力。b = 60 mm,h = 100 mm。 解题分析: 从图中可分析 1、4 点是单向应力状态,2 点在中性轴上为纯剪切应力状态,3 1 取平行和垂直与梁横截面的六个平面,构成微体。则各点处的应力状态如图示。 2、 梁截面惯性矩为 点微体上既有正应力又有切应力。 解: 、画各点处微体的应力状态图 计算各点处主应力 8 4 3 3 3 3 4 500 10 m 12 60 10 (100 10 m 12 − − − = × × × × = = bh ) I z 1 点处弯曲正应力(压应力) 100 10 Pa 100MPa 500 10 m 10 10 N m 50 10 m 6 8 4 −3 3 = × = × × ⋅ × × = = − − z I My σ 1 点为单向压缩受力状态,所以 σ 1 = σ 2 = 0 , 100MPa σ 3 = − 2 点为纯剪切应力状态, 30 10 Pa 30MPa 2 60 100 10 m 3 120 10 N 6 6 2 3 = × = × × × × × = − τ (向下) 容易得到, 30MPa σ 1 = ,σ 2 = 0, 30MPa σ 3 = − 3 点为一般平面应力状态 弯曲正应力 50 10 Pa 50MPa 500 10 m 10 10 N m 25 10 m 6 8 4 3 3 = × = × × ⋅ × × = = − − z I My σ 弯曲切应力 σ1 4 τ 2 FS=120 kN 题 1 图 中性轴 3 2 4 h σ 25 mm τ 3 b 1 M=10 kN·m σ3 1 50 mm 1

:=FS.120x102N×60x25x375x10*m-250x10ea-25Mm bl, 60x10-m×500x10-m 2 2 2 -8.6MPa 所以o,=58.6MPa,o2=0,3=-8.6MPa 4点为单向拉伸应力状态,拉伸正应力的大小与1点相等。所以4点的主应力为 G,=100MPa,2==0 2试求图示微体斜截面上的应力,主应力及其方位,并求最大切应力。 20 MP 图2 解题分析:所要计算的斜截面外法线与x轴的夹角:为正60°。斜截面应力计算公式中, 角正负号规定为自x轴正向逆时针转向外法线为正。 解:1、计算斜截面上应力 选取xy坐标系,如图示。则该微体各应力为 ,=40MPa,=20MPa,=10MPa =60°斜截面上的应力为 .=0+0,0cos2a-,sm20 =40+20)MP+40-20》MPa cos120°-10 MPasin120°=163MPa 2 2
22.50 10 Pa 22.5MPa 60 10 m 500 10 m 120 10 N 60 25 37.5 10 m 6 3 8 4 * 3 9 3 S = × = × × × × × × × × = = − − − z z bI F S τ 8.6MPa 58.6MPa ) (22.5 10 Pa) 2 50 10 Pa ( 2 50 10 Pa ) 2 ( 2 2 6 2 6 6 2 2 min max − + × = × ± × = + − ± + = x x y x y τ σ σ σ σ σ σ 所以 58.6MPa σ 1 = ,σ 2 = 0, 8.6MPa σ 3 = − 4 点为单向拉伸应力状态,拉伸正应力的大小与 1 点相等。所以 4 点的主应力为 100MPa σ 1 = ,σ 2 =σ 3 = 0 2 试求图示微体斜截面上的应力,主应力及其方位,并求最大切应力。 解题分析: 所要计算的斜截面外法线与 x 轴的夹角α 为正 。斜截面应力计算公式中, D 60 α 角正负号规定为自 x 轴正向逆时针转向外法线为正。 解:1、计算斜截面上应力 选取 x y 坐标系,如图示。则该微体各应力为 = 40MPa σ x , = 20MPa σ y , =10MPa x τ D α = 60 斜截面上的应力为 cos120 10MPa sin120 16.3MPa 2 40 20 MPa 2 40 20 MPa cos 2 sin 2 2 2 − = − + + = − − + + = ( ) ( ) D D α τ α σ σ σ σ σ α x x y x y 22.5o 10 MPa x σ2 y 20 MPa 40 MPa 30o 图 2 2

-00m2a+,s2 -40-20MPen120°+10MPac0s120=3.66MPa 2、计算主应力及其方位 =±0* .020±r+0w-份 2 2 所以主应力为G1=44.1MPa,o2=15.9MPa,G3=0 由公式tana,=一 t,一得 0.-0an =arctan(=actan(-0 MPa-15 MPa2 t 10MPa 所以主应力,对应的方位为-22.5 3、计算最大切应力 7e=:9.4Ma-02M 讨论:当采用公式tan2a,= 2红计算时,得a=-225或0=675.这时往往不 0.-0, 能直观判定方位角a=-225°对应的是,的方位或是。,的方位。采用公式 工一计算时,可以避免这一问题。 3自受力构件内取一微体,其上承受应力如图a所示,:,=σ1√万。试求此点的主应力及主 平面微体。 3
sin120 10MPa cos120 3.66MPa 2 40 20 MPa sin 2 cos 2 2 + = − = + − = ( ) D D α τ α σ σ τ α x x y 2、计算主应力及其方位 ⎩ ⎨ ⎧ + = − ± + = + − ± + = 15.9MPa 44.1MPa ) 10MPa 2 40 20 MPa ( 2 40 20 MPa ) 2 ( 2 2 2 2 2 min max ( ) ( ) ( ) x x y x y τ σ σ σ σ σ 所以主应力为 44.1MPa σ 1 = , 15.9MPa σ 2 = ,σ 3 = 0 由公式 min 0 tan σ σ τ α − = − x x 得 D ) 22.5 40 MPa 15.9 MPa 10 MPa arctan( ) arctan( min 0 = − − = − − = − σ σ τ α x x 所以主应力σ 1 对应的方位为 − 22.5D 。 3、计算最大切应力 22.1MPa 2 44.1MPa 0 2 1 3 max = − = − = σ σ τ 讨论:当采用公式 x y x σ σ τ α − = − 2 tan 2 0 计算时,得 或 。这时往往不 能直观判 定方位角 对应的是 D α 0 = −22.5 D α 0 = 67.5 D 22.5 α 0 = − σ 1 的方位或 是 σ 2 的方位 。采用公 式 min 0 tan σ σ τ α − = − x x 或 y x σ σ τ α − = − max 0 tan 计算时,可以避免这一问题。 3 自受力构件内取一微体,其上承受应力如图 a 所示,τ x =σ / 3 。试求此点的主应力及主 平面微体。 σ a a τ 3 (a) (b) (c) σ d b τ y x σ/3 σ/3 σ τ τx σ x c b σ 60o 60o 题 3 图

解题分析:本题微体为一三角体。为使用极值应力计算公式,应首先建立直角坐标系并确定 。,、·,和?·微体处于静力平衡状态,所以从其上切取的任何一块也应处于静力平衡状态。 在建立直角坐标系后,利用上述关系可计算出。,、G,和x,。 解:从三角形微体中取出一直角三角形ab,并建立直角坐标系,如图b所示。图b中, ∠adb=90°,并用4表示ab斜面面积。设在ad截面上设正应力为ox、切应力为tx·当将微 体abc从中间竖直切开后,由于左右对称性,所以截开面ad上的剪应力必为零,即x,=0。由 剪应力互等定理知db边上切应力也为零。所以,可以确定ad面和db面即是该点的主平面。 由于直角三角形adb微体处于平衡状态,于是有 ∑F=0,rAa sin30°+x Aa cos30°=0,得 0,=-15=-6/3(压) 所以该点处主应力为0,=0,0=0,=-G/3。 4构件中某点A为平面应力状态,两斜截面上的应力如图ā所示。试用应力圆求主应力和 最大切应力。 209 D(-100.50 10 (a) 题4图 解题分析:木题应理解为已知了A点处微体两个斜截面上的应力,或者说已知了应力圆上 的两个点。但是,已知圆上的两个点并不能确定这个圆,所以还需要补充一个条件。这个补 充条件是:应力圆的圆心必在横坐标轴(即σ轴)上。 解:1、建立。、T坐标系(见图b) 2、在坐标图上确定点D(200,100)和点D(-100,50),连接D、D1.做DD,线的中垂线, 交于。轴上C点。以C点为圆心,CD为半径作圆,即为所求之应力圆。 3、在应力圆上最取G1=235MPa,o2=0,o3=-110MPa
解题分析:本题微体为一三角体。为使用极值应力计算公式,应首先建立直角坐标系并确定 σ x 、σ y 和 x τ 。微体处于静力平衡状态,所以从其上切取的任何一块也应处于静力平衡状态。 在建立直角坐标系后,利用上述关系可计算出σ x 、σ y 和 x τ 。 解:从三角形微体中取出一直角三角形adb,并建立直角坐标系,如图b所示。图b 中, D ∠adb = 90 ,并用Aab表示ab斜面面积。设在ad截面上设正应力为σ x 、切应力为 x τ 。当将 竖直切开后,由于左右对称性,所以截开面ad上的剪应力必为零,即 = 0 微 体abc从中间 x τ 。由 剪应力互等定理知db边上切应力也为零。所以,可以确定ad面和db面即是该点的主平面。 由于直角三角形 adb 微体处于平衡状态,于是有 ∑ = 0 Fx , sin 30 + cos 30 = 0 D D Aab σ x Aab τ ,得 σ x = −τ / 3 = −σ / 3 (压) 所以该点处主应力为σ 1 =σ ,σ 2 = 0,σ 3 = −σ / 3。 4 构 力状态 两斜截 上的应力如 a 所示。试用应力圆求主应力和 解题分析 件中某点 A 为平面应 , 面 图 最大切应力。 100 100 200 50 A D(200,100) D1(-100,50) τ O C σ1 τmax σ σ3 (a) (b) 题 4 图 : 本题应理解为已知了 A 点处微体两个斜截面上的应力,或者说已知了应力圆上 的两个点。但是,已知圆上的两个点并不能确定这个圆,所以还需要补充一个条件。这个补 充条件是:应力圆的圆心必在横坐标轴(即σ 轴)上。 解:1、建立σ 、τ 坐标系(见图 b) 2、在坐标图上确定点D(200,100)和点D1(-100,50),连接D、D1,做DD1线的中垂线, 交于σ 轴上C点。以C点为圆心,CD为半径作圆,即为所求之应力圆。 在应力圆上量取 235MPa 3、 σ 1 = ,σ 2 = 0, 110MPa σ 3 = − 。 4
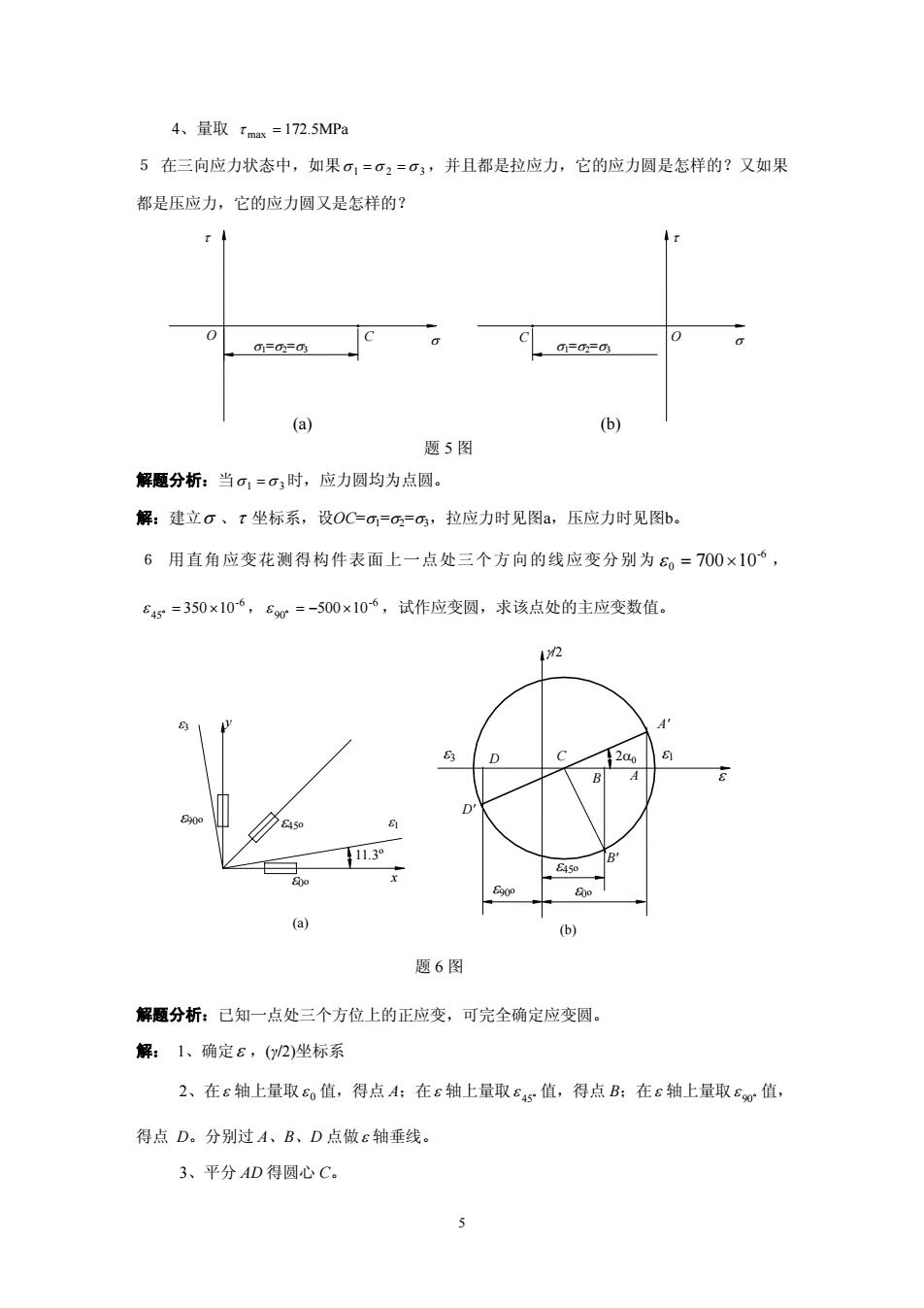
4、量取tax=172.5MP 5在三向应力状态中,如果,=2=,并且都是拉应力,它的应力圆是怎样的?又如果 都是压应力,它的应力圆又是怎样的? 00 (a) 题5图 解题分析:当,=,时,应力圆均为点圆。 解:建立o、t坐标系,设OC===,拉应力时见图a,压应力时见图b 6用直角应变花测得构件表面上一点处三个方向的线应变分别为6。=700×106, £5=350×106,£=-500x106,试作应变圆,求该点处的主应变数值 12 11.3 (a) (b) 题6图 解题分析:已知一点处三个方位上的正应变,可完全确定应变圆。 解:1、确定6,02)坐标系 2、在E轴上量取o值,得点A:在£轴上量取Es值,得点B:在£轴上量取E值, 得点D。分别过A、B、D点做ε轴垂线。 3、平分AD得圆心C
4、量取 τ max = 172.5MPa 5 在三向应力状态中,如果σ 1 =σ 2 =σ 3 ,并且都是拉应力,它的应力圆是怎样的?又如果 怎样的? 都是压应力,它的应力圆又是 τ 解题分析:当σ 1 =σ 3时,应力圆均为点圆。 解:建立σ 、τ 坐标 应力时见图a,压应力时见图b。 700×10 , D D 系,设OC=σ1=σ2=σ3,拉 6 用直角应变花测得构件表面上一点处三个方向的线应变分别为 ε 0 = -6 -6 ε = 350 ×10 , -6 45 ε 90 = −500×10 ,试作应变圆,求该点处的主应变数值。 解题分析:已知一点处三个方位上的正应变,可完全确定应变圆。 解: 1、确定ε ,(γ/2)坐标系 2、在ε 轴上量取 0 ε 值,得点 A;在ε 轴上量取 D 45 ε 值,得点 B;在ε 轴上量取 D 90 ε 值, 得点 D。分别过 A、B、D 点做ε 轴垂线。 3、平分 AD 得圆心 C。 D' B' A' 11.3o y ε x 0o ε45o ε90o ε1 ε3 ε3 ε90o ε45o ε0o γ/2 D C ε1 B A ε 题 6 图 2α (b) (a) (b) C τ C O σ σ1=σ2=σ3 O σ1=σ2=σ3 题 5 图 σ 0 (a) 5

4、在D点向上最取DD=CB。 5、连DC即为应变圆半径,作应变圆交£轴于和3两点,则,和6,即为主应变数值。 6、连C,∠AC8=2a,即可得主应变6与6n的夹角ao。 7、结果6=750×10,63=-550×105,ag=113 讨论:可以证明:在直角三角形CDD及三角形CBB中,CD=CB=应变圆半径。 △CDD'≌△BBC,故DD=CB 7边长为20mm的钢立方体置于钢模中,在顶面上受力F=14kN作用。已知u=0.3,假设 钢模的变形以及立方体与钢模之间的摩擦力可以忽略不计。试求立方体各个面上的正应力。 F-14kN 题7图 解题分析:钢立方体置于钢模中,在y方向有应力,、:方向限制钢立方体变形,即6,=0、 6.=0,以此可求出c,和c:· F 14×103N 挪1小6,-72020210a-35x10a-35Mm 2、因有钢模限制,所以x、:方向的应变均为零。 6,.-g,+al-0 -0.3x(-35MPa+a:)=0 a 4.-M6,to2-0 g:-0.3x(-35MPa+cz)=0 (b) 联立(a、(b)两式,得 o:=c,=-15MP (压) 6
4、在 D 点向上量取 DD'= CB。 5、连 D'C 即为应变圆半径,作应变圆交ε 轴于 1 ε 和 3 ε 两点,则 1 ε 和 3 ε 即为主应变数值。 6、连CA',∠A'C 1 ε =2α0,即可得主应变 1 ε 与 0 ε 的夹角α 0 。 7 -6 、结果 750 , -6 D ε = × , 讨论 角三角形 CDD'及三角形 CBB CD'= CB'= 应变圆半径。 7 中,在顶面上受力 F = 14 kN 作用。已知 1 10 3 ε = −550 ×10 11.3 α 0 = :可以证明:在直 '中, △CDD'≌△B'BC,故 DD'= CB 边长为 20 mm 的钢立方体置于钢模 µ = 0.3,假设 解题分析:钢立方体置于钢模中, x、z 方向限制钢立方体变形,即 钢模的变形以及立方体与钢模之间的摩擦力可以忽略不计。试求立方体各个面上的正应力。 F=14kN 在 y 方向有应力, ε x = 0 、 ε z = 0 ,以此可求出σ x 和σ z 。 解:1、 35 10 Pa 35 MPa 2 10 m 14 10 N3 × × − A F y 20 0 6 6 2 = − × = − × σ = − = − 2、因有钢模限制,所以 x、z 方向的应变均为零。 0 ( ) = − + = E x y z x σ µ σ σ ε σ x − 0.3×(−35 MPa +σ z ) = 0 (a) 0 ( ) = − + = E z y x z σ µ σ σ ε σ z − 0.3×(−35 MPa +σ x ) = 0 (b) 联立(a)、(b)两式,得 = = −15 MPa σ z σ x x z y 题 7 图 (压) 6