
第三章扭转 §3.1扭转的概念和实例 §3.2外力偶矩的计算,扭矩和扭矩图 §3.3纯剪切 §3.4圆轴扭转时的应力 §3.5圆轴扭转时的变形 §3.6圆柱形密圈螺旋弹簧的应力和变形 §3.7非圆截面杆扭转的概念 §3.1扭转的概念和实例 1.实例如: 〔车床的光杆 反应釜的搅拌轴 、汽车转向轴 2.扭转:在杆件的两端作用等值,反向且作用面垂直于杆件轴线的一对 力偶时,杆的任意两个横截面都发生绕轴线的相对转动,这种变形称为 扭转变形。 §3.2外力偶矩的计算,扭矩和扭矩图 1.M、m、P之间的关系 M。一一外力偶矩(Nm) n一一转速(r/min) P-功率(kW)(1kW=1000Nms)(马力)(1马力=735.5W〉 每秒钟内完成的功力 M号-10o0P或
第三章 扭 转 §3.1 扭转的概念和实例 §3.2 外力偶矩的计算,扭矩和扭矩图 §3.3 纯剪切 §3.4 圆轴扭转时的应力 §3.5 圆轴扭转时的变形 §3.6 圆柱形密圈螺旋弹簧的应力和变形 §3.7 非圆截面杆扭转的概念 §3.1 扭转的概念和实例 1.实例如: 车床的光杆 反应釜的搅拌轴 汽车转向轴 2.扭转:在杆件的两端作用等值,反向且作用面垂直于杆件轴线的一对 力偶时,杆的任意两个横截面都发生绕轴线的相对转动,这种变形称为 扭转变形。 §3.2 外力偶矩的计算,扭矩和扭矩图 1.Me、m、 P 之间的关系 Me——外力偶矩(N∙m) n——转速(r/min) P——功率(kW)(1kW=1000N∙m/s)(马力)(1 马力=735.5W) 每秒钟内完成的功力 P n M e 1000 60 2 · = 或

M,20=55 (=9549 ew r/min 仙wn=7024P9力 nr/min 2.扭矩和扭矩图 m e (b) (c) (1)截面法、平衡方程 ΣM=0T-M=0 T=M (2)扭矩符号规定:为无论用部分I或部分Ⅱ求出的同一截面上的 扭矩不但数值相同且符号相同、扭矩用右手螺旋定则确定正负号。 (3)扭矩图 例1主动轮A输入功率PA=50kW,从动轮输出功率PB=P=15kW Po=20kW,=300rmin,试求扭矩图. 解:(1) -%-9器-591Nm 15 MeB T1 Ma=Me=9549×300=477N-m () Mp =637N.m (2)求T ΣM=0T+MeB=0 T=-MeB=-477 T2-Me+Mo=0 T2=1115N 1115Nm T3-MeD=0 T;=MoF-63T e e 447N,m
P n M e 735.5 60 2 · = / min 7024 / min kW 9549 . . n r P M n r P M e N m e N m 马力 = = 2.扭矩和扭矩图 (1)截面法、平衡方程 ΣMx=0 T-Me=0 T=Me (2)扭矩符号规定:为无论用部分 I 或部分 II 求出的同一截面上的 扭矩不但数值相同且符号相同、扭矩用右手螺旋定则确定正负号。 (3)扭矩图 例 1 主动轮 A 输入功率 PA=50kW,从动轮输出功率 PB=PC=15kW, PD=20kW,n=300r/min,试求扭矩图. 解:(1) 1591 300 50 = 9549 = 9549 = n P M eA Nm 637N m 477N m 300 15 9549 = = = = eD eB eC M M M (2)求 T ΣMx=0 T1+MeB=0 T1=-MeB=-477 T2-MeA+MeB=0 T2=1115N T3-MeD=0 T3=Med=63T
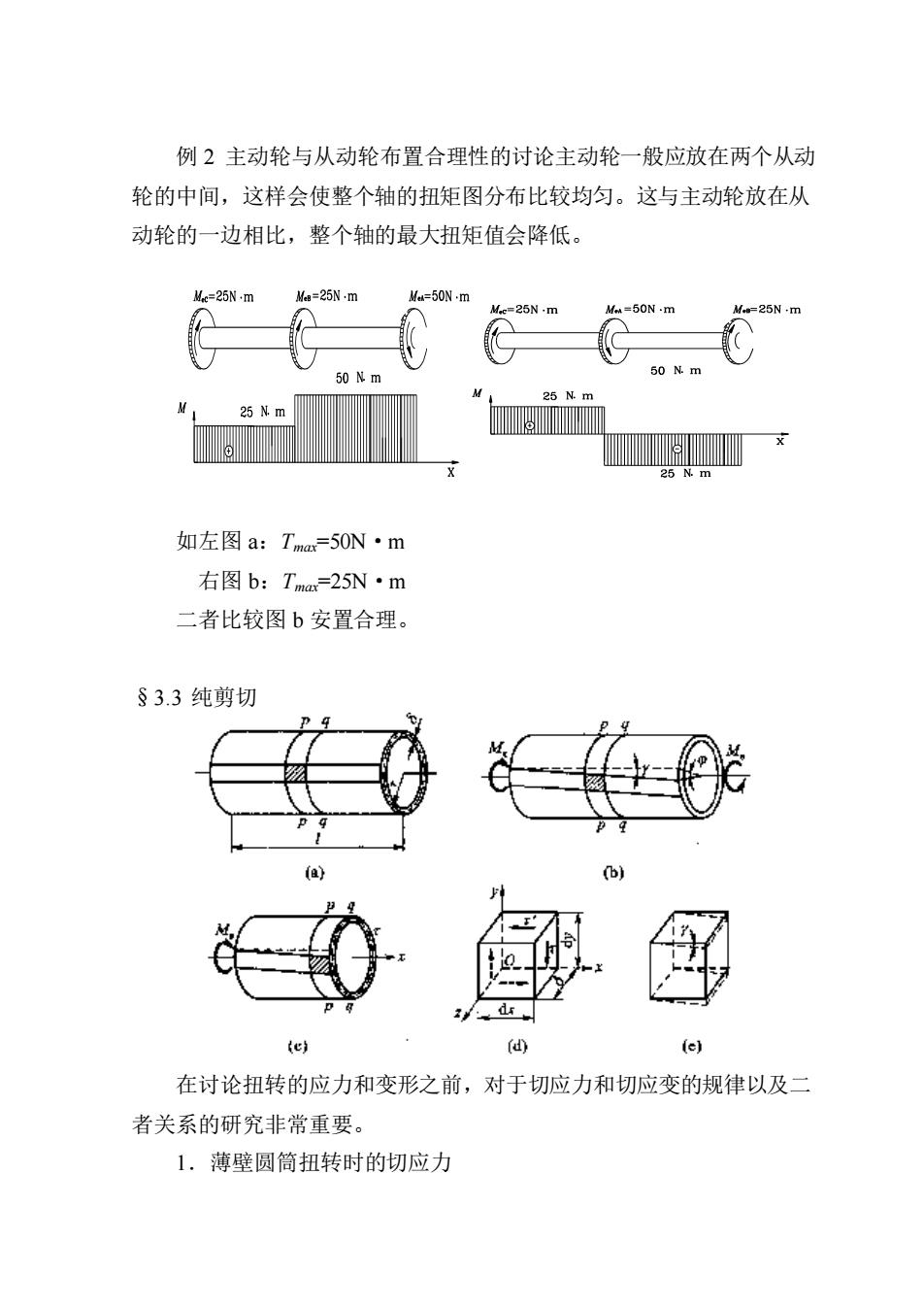
例2主动轮与从动轮布置合理性的讨论主动轮一般应放在两个从动 轮的中间,这样会使整个轴的扭矩图分布比较均匀。这与主动轮放在从 动轮的一边相比,整个轴的最大扭矩值会降低。 0 N m 5 N.m 如左图a:Tma=50N·m 右图b:Tma=25N·m 二者比较图b安置合理。 §3.3纯剪切 (b (eh d 在讨论扭转的应力和变形之前,对于切应力和切应变的规律以及二 者关系的研究非常重要。 1.薄壁圆筒扭转时的切应力
例 2 主动轮与从动轮布置合理性的讨论主动轮一般应放在两个从动 轮的中间,这样会使整个轴的扭矩图分布比较均匀。这与主动轮放在从 动轮的一边相比,整个轴的最大扭矩值会降低。 如左图 a:Tmax=50N·m 右图 b:Tmax=25N·m 二者比较图 b 安置合理。 §3.3 纯剪切 在讨论扭转的应力和变形之前,对于切应力和切应变的规律以及二 者关系的研究非常重要。 1.薄壁圆筒扭转时的切应力

连接件的剪切面上非但有切应力,而且有正应 力,剪切面附近变形十分复杂。纯剪切是指截面上 只有切应力而无正应力。纯剪切的典型例子薄壁圆 筒的扭转。 (1)观察变形及分析 变形前纵线与圆周线形成方格。 变形后方格左右两边相对错动,距离保持不变,圆周半径长度保持 不变,这表示横截面上无正应力,只有切应力。由于切应变发生在纵截 面,故横截面上的切应力与半径正交。 对薄壁圆筒而言,切应力沿壁厚不变化。 (2)力矩平衡ΣM,=0 M。=2m6t t=2m8 M 2.切应力互等定理 取出单元体如左图 ”品 ΣF=0 ΣM=0 (r动h=(r' T/=T 在相互垂直的两个平面上,切应力必 M 然成对存在,且数值相等,其方向都垂直 于两平面交线,或共同指向或共同背离两 平面交线。这就是切应力互等定理,也称 为切应力双生定理。 3.切应变剪切胡克定律 上述单元体,属于纯剪切状态 P曲线 钢筋筒的扭转试验
连接件的剪切面上非但有切应力,而且有正应 力,剪切面附近变形十分复杂。纯剪切是指截面上 只有切应力而无正应力。纯剪切的典型例子薄壁圆 筒的扭转。 (1)观察变形及分析 变形前纵线与圆周线形成方格。 变形后方格左右两边相对错动,距离保持不变,圆周半径长度保持 不变,这表示横截面上无正应力,只有切应力。由于切应变发生在纵截 面,故横截面上的切应力与半径正交。 对薄壁圆筒而言,切应力沿壁厚不变化。 (2)力矩平衡ΣMx=0 2 2 2 ·· r M M r r e e = = 2.切应力互等定理 取出单元体如左图 2 2 r M e = ΣFx=0 τ′=τ′ ΣMz=0 (dy)dx = ( dx)dy τ′=τ 在相互垂直的两个平面上,切应力必 然成对存在,且数值相等,其方向都垂直 于两平面交线,或共同指向或共同背离两 平面交线。这就是切应力互等定理,也称 为切应力双生定理。 3.切应变剪切胡克定律 上述单元体,属于纯剪切状态
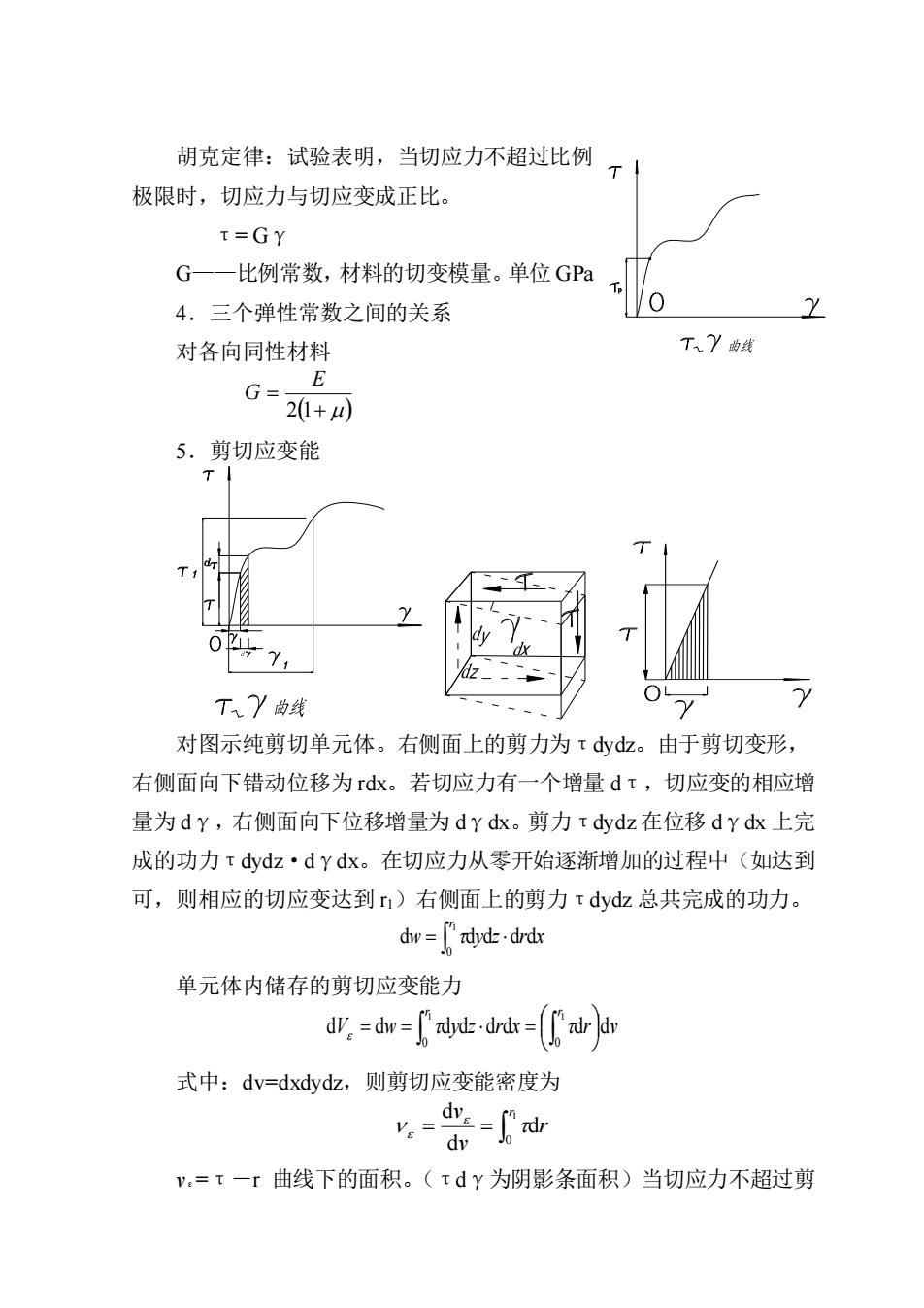
胡克定律:试验表明,当切应力不超过比例 T 极限时,切应力与切应变成正比。 t=GY G一一比例常数,材料的切变模量。单位GPa 4.三个弹性常数之间的关系 对各向同性材料 T、Y线 G=20+ 5.剪切应变能 0Y: TY曲线 对图示纯剪切单元体。右侧面上的剪力为Tydz。由于剪切变形, 右侧面向下错动位移为rdx。若切应力有一个增量dτ,切应变的相应增 量为dY,右侧面向下位移增量为dYdx。剪力tydz在位移dYdx上完 成的功力rdydz·dYdx。在切应力从零开始逐渐增加的过程中(如达到 可,则相应的切应变达到)右侧面上的剪力r dydz总共完成的功力。 d邮=tdt 单元体内储存的剪切应变能力 d业.=d咖==dh 式中:dv=dxdydz,则剪切应变能密度为 g品-地 v=t一r曲线下的面积。(tdY为阴影条面积)当切应力不超过剪
胡克定律:试验表明,当切应力不超过比例 极限时,切应力与切应变成正比。 τ= Gγ G——比例常数,材料的切变模量。单位 GPa 4.三个弹性常数之间的关系 对各向同性材料 ( + ) = 2 1 E G 5.剪切应变能 对图示纯剪切单元体。右侧面上的剪力为τdydz。由于剪切变形, 右侧面向下错动位移为 rdx。若切应力有一个增量 dτ,切应变的相应增 量为 dγ,右侧面向下位移增量为 dγdx。剪力τdydz 在位移 dγdx 上完 成的功力τdydz·dγdx。在切应力从零开始逐渐增加的过程中(如达到 可,则相应的切应变达到 r1)右侧面上的剪力τdydz 总共完成的功力。 = 1 0 d d d d d r w y z r x 单元体内储存的剪切应变能力 = = = 1 1 0 0 d d d d d d d d r r V w y z r x r v 式中:dv=dxdydz,则剪切应变能密度为 = = 1 0 d d d r r v v vε=τ-r 曲线下的面积。(τdγ为阴影条面积)当切应力不超过剪

切比例极限的情况下。τ与Y的关系为斜直线(为线弹性情况) v.-3m 剪切胡克定律:t=GY,则 v:=2π=2G §3.4圆轴扭转时的应力 1.应力分布规律:「几何学方面 D 物理学方面 (静力学方面 (1)变形几何关系 ①观察试验(在小变形前提下) a.圆周线大小、形状及相邻二圆 周线之间的距离保持不变,仅绕轴线 相对转过一个角度。 b.在小变形前提下纵线仍为直线 仅倾斜一微小角度,变形前表面的矩形方格,变形后错动成菱形。 ②平面假设:圆轴扭转变形前的平面横截面变形后仍保持平面,形 状和大小不变,半径仍保持为直线:且相邻二截面间的距离保持不变。 ③结论:横截面上只有切应力而无正应力。 ④取dx一段轴讨论: rdx Rdo r=Rdo dx (a) 讨论: a. 为扭转角中沿轴线×的变化率对给定截面上的各点而言,(即 dx
切比例极限的情况下。τ与γ的关系为斜直线(为线弹性情况) r 2 1 = 剪切胡克定律:τ=Gγ,则 G r 2 2 1 2 = = §3.4 圆轴扭转时的应力 1.应力分布规律: 几何学方面 物理学方面 静力学方面 (1)变形几何关系 ①观察试验(在小变形前提下) a.圆周线大小、形状及相邻二圆 周线之间的距离保持不变,仅绕轴线 相对转过一个角度。 b.在小变形前提下纵线仍为直线 仅倾斜一微小角度,变形前表面的矩形方格,变形后错动成菱形。 ②平面假设:圆轴扭转变形前的平面横截面变形后仍保持平面,形 状和大小不变,半径仍保持为直线;且相邻二截面间的距离保持不变。 ③结论:横截面上只有切应力而无正应力。 ④取 dx 一段轴讨论: x r R r x R d d d d = = x r d d = (a) 讨论: a. dx d 为扭转角φ沿轴线 x 的变化率对给定截面上的各点而言,(即

x相同)它是常量。 b.横截面上任意点的切应变Yp与该点到圆心的距离P成正比。(任 意半径圆周处的切应变均相等)。 (2)物理关系 ①剪切胡克定律 t。=Gr 5,=6 (b) ②结论 a.距圆心等距的圆周上各点处的切应力 均相等。T与半径垂直(即各点处的圆周切 线方向)。 b.切应力沿半径直线分布。 (3)静力关系 ①内力为分布力系的合力 T=pr,aA=G.pd4 令I。=∫,pd4(截面对圆心0的板惯 性矩) T=G, dx Tp d 于是: (c) R 式(c)代入式(b)得 2 (d) ②讨论
x 相同)它是常量。 b. 横截面上任意点的切应变γP 与该点到圆心的距离 P 成正比。(任 意半径圆周处的切应变均相等)。 (2)物理关系 ①剪切胡克定律 = Gr dx d p G = (b) ②结论 a. 距圆心等距的圆周上各点处的切应力 均相等。τP与半径垂直(即各点处的圆周切 线方向)。 b. 切应力沿半径直线分布。 (3)静力关系 ①内力为分布力系的合力 = A = A dA dx d T dA G 2 令 = A I dA 2 (截面对圆心 O 的板惯 性矩) dx d T GI P = 于是: GI P T dx d = (c) 式(c)代入式(b)得 I T = (d) ②讨论
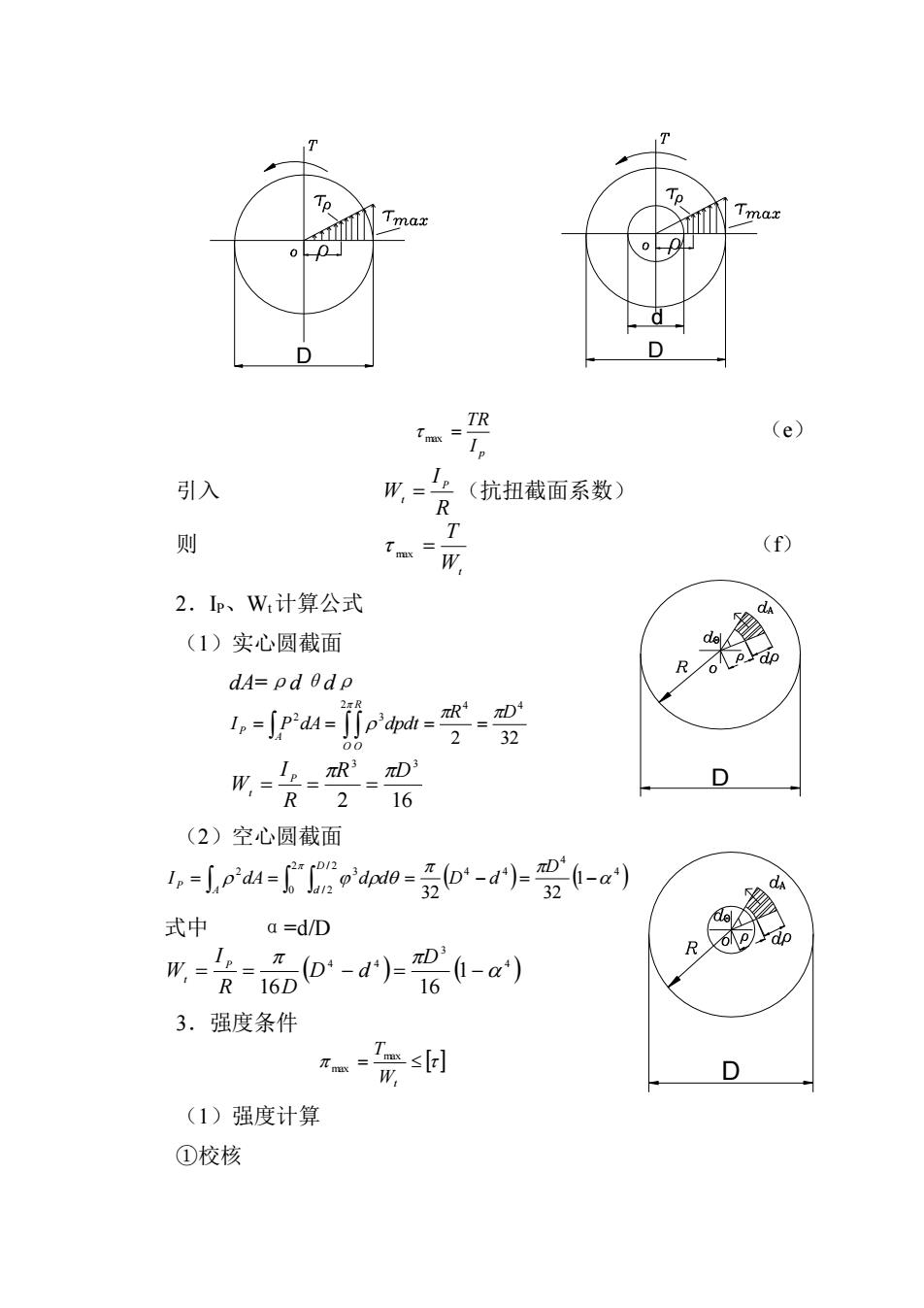
(e) 引入 用=台(抗扭裁面系数) R 多 t.-W, 2.p、W,计算公式 (1)实心圆截面 dA=pd odp I,=Spidu=iio'dod 2=32 斯会警g D (2)空心圆截面 ,=ph=oda0=o-ar受-a 式中 a =d/D 3.强度条件 D (1)强度计算 ①校核
D D d p I TR max = (e) 引入 R I W P t = (抗扭截面系数) 则 Wt T max = (f) 2.IP、Wt计算公式 (1)实心圆截面 dA=ρdθdρ = = = = 2 4 4 2 3 2 32 O R O A P R D I P dA dpdt 2 16 3 3 R D R I W P t = = = (2)空心圆截面 ( ) ( ) 4 4 4 4 2 0 / 2 / 2 2 3 1 32 32 = = = − = − D I dA d d D d D A d P 式中 α=d/D ( ) ( ) 4 3 4 4 1 16 16 = = − = − D D d R D I W P t 3.强度条件 = Wt Tmax max (1)强度计算 ①校核 D D

②设计截面W,之司 πD3、T 162同 D≥ 16T, 阿 0-简 16T D2-a) ③确定许用载荷Tmax≤[t]W, (2)讨论:对变截面杆、如阶梯杆、圆锥形杆,W,不是常量,tm 并不一定发生在扭矩为T的截面上,这要综合考虑T和W寻求:最 大值。 4.强度计算举例 Examplel图示传动轴 Given Me1=895N·mMe2=538N·m 47(N.m) Me=2866N·mM4=1075N·m Mes=358N·m[t]=20MPa 895T Find设计阶梯轴各段的直径D o Procedure:(序号)solution 358 43 (1)求各段轴的扭矩,作出扭矩图 (2)求各段轴的直径D wz同 πD3、T 16≥可 隔 D23≥71.5mm D4≥71.5mm D4s≥45mm
②设计截面 T max Wt max 3 16 D T 3 16 max T D ( ) 4 max 3 1 16 D T − ( ) 3 4 max 1 16 − T D ③确定许用载荷 Tmax≤[τ]Wt (2)讨论:对变截面杆、如阶梯杆、圆锥形杆,Wt不是常量,τmax 并不一定发生在扭矩为 Tmax的截面上,这要综合考虑T 和 Wt寻求 T = 最 大值。 4.强度计算举例 Example1 图示传动轴 Given Me1=895N·m Me2=538N·m Me3=2866N·m Me4=1075N·m Me5=358N·m [τ]=20MPa Find 设计阶梯轴各段的直径 D Procedure:(序号)solution (1)求各段轴的扭矩,作出扭矩图 (2)求各段轴的直径 D ∵ T Wt D T 16 3 ∴ 3 16 T D 61.1mm 20 16 895 1000 3 12 = D D23≥71.5mm D34≥71.5mm D45≥45mm 895 1433 358
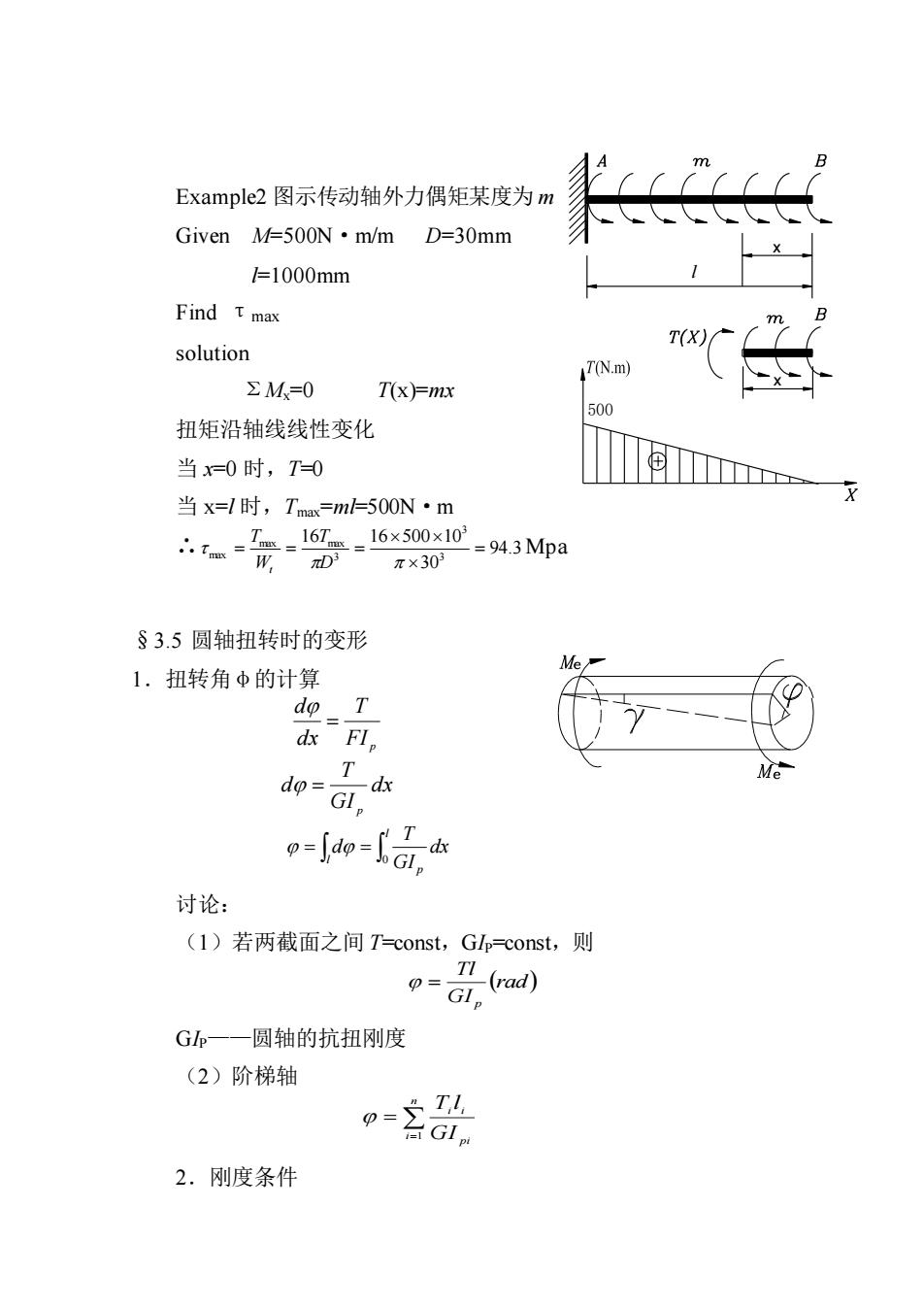
Example2图示传动轴外力偶矩某度为m Given M=500N.m/m D=30mm =1000mm Find t max T(X) solution 47(N.m) ΣM=0 T(x=mx 500 扭矩沿轴线线性变化 当x=0时,T=0 当x=时,Ta=mi-50ON·m -=94.3Mpa W ×30 §3.5圆轴扭转时的变形 1.扭转角中的计算 do T dx Fl, T do-l -o-品 讨论: (1)若两截面之间T-const,Glp-const,.则 G一一圆轴的抗扭刚度 (2)阶梯轴 -器 2.刚度条件
Example2 图示传动轴外力偶矩某度为 m Given M=500N·m/m D=30mm l=1000mm Find τmax solution ΣMx=0 T(x)=mx 扭矩沿轴线线性变化 当 x=0 时,T=0 当 x=l 时,Tmax=ml=500N·m ∴ 94.3 30 16 16 500 10 3 3 3 max max max = = = = D T W T t Mpa §3.5 圆轴扭转时的变形 1.扭转角φ的计算 FI p T dx d = dx GI T d p = = = l p l dx GI T d 0 讨论: (1)若两截面之间 T=const,GIP=const,则 (rad ) GI Tl p = GIP——圆轴的抗扭刚度 (2)阶梯轴 = = n i pi i i GI T l 1 2.刚度条件 500 l x x