
第13章 弯曲变形 梁的位移) Deflection of Beams
弯曲变形 (梁的位移) Deflection of Beams 第 13 章
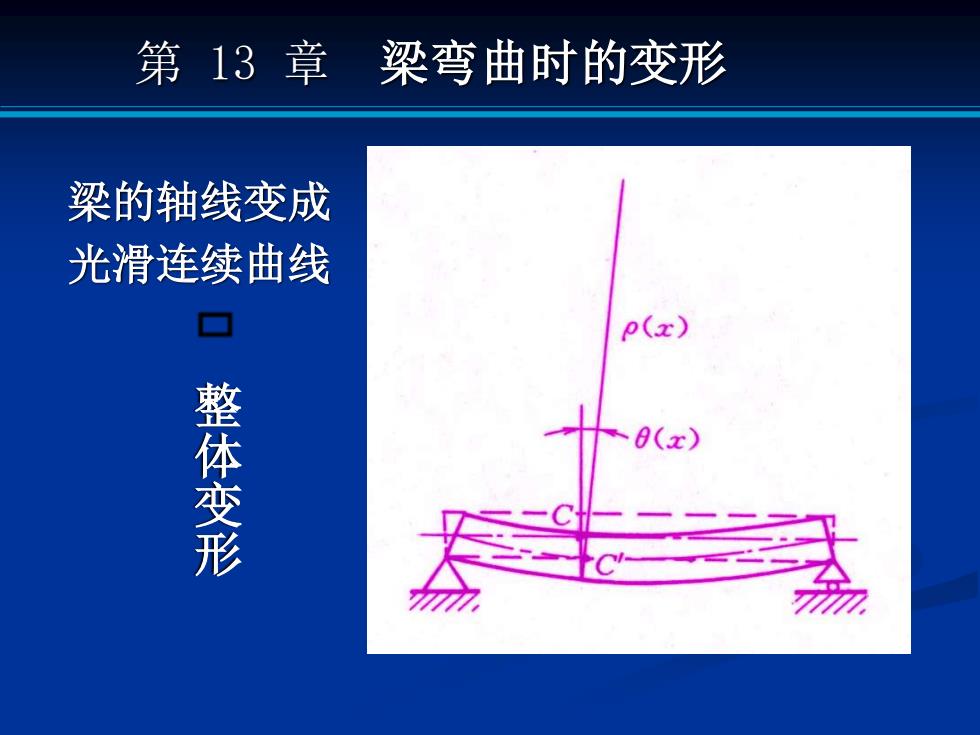
第13章 梁弯曲时的变形 梁的轴线变成 光滑连续曲线 p(x) 整体变形 0(x)
第 13 章 梁弯曲时的变形 整 体 变 形 梁的轴线变成 光滑连续曲线

第13章梁弯曲时的变形 挠度w (deflection) p(x) 梁的位移 转角0 0(x) (slope w(x) 挠度曲线 dw 0= dx
梁 的 位 移 挠度w (deflection) 转角 (slope) = dw dx 第 13 章 梁弯曲时的变形

§13-1确定梁位移的积分方法 对于拉伸(压缩)、 扭转位移—定积分 对于梁的位移—不定积分 弹性曲线的小挠度微分方程
§13-1 确定梁位移的积分方法 对于拉伸(压缩)、扭转位移⎯定积分 对于梁的位移⎯不定积分 弹性曲线的小挠度微分方程
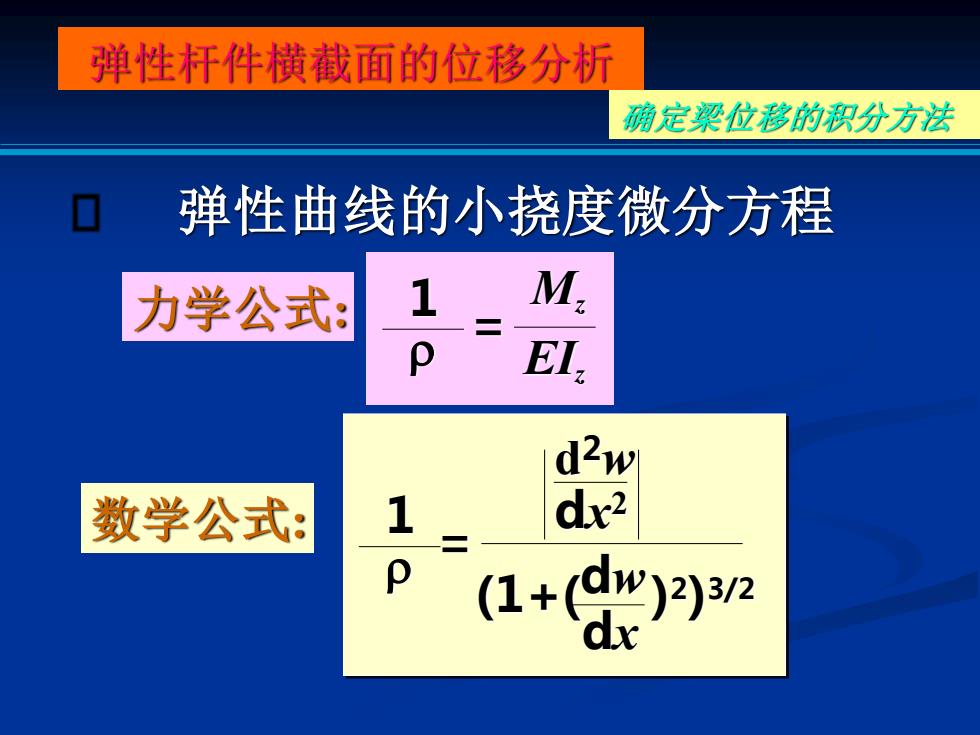
弹性杆件横截面的位移分析 确定梁位移的积分方法 弹性曲线的小挠度微分方程 力学公式: 1 M. EI. d2w 数学公式: 1 dx2
确定梁位移的积分方法 弹性曲线的小挠度微分方程 力学公式: 数学公式: 弹性杆件横截面的位移分析 = 1 d 2w dx 2 (1+( dw dx ) 2) 3/2 1 = Mz EIz
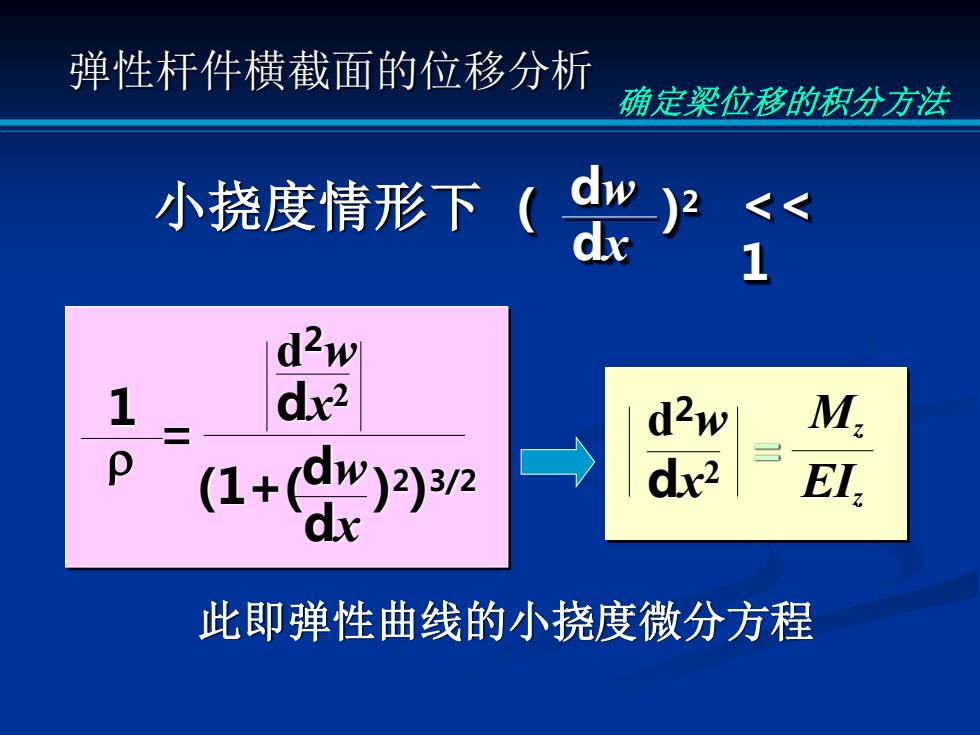
弹性杆件横截面的位移分析 确定梁位移的积分方法 小挠度情形下( dw dx 2 1 d2w dx2 d2w M. dx2 EI. 此即弹性曲线的小挠度微分方程
确定梁位移的积分方法 小挠度情形下 ( dw dx ) 2 << 1 此即弹性曲线的小挠度微分方程 弹性杆件横截面的位移分析 = 1 d 2w dx 2 (1+( dw dx ) 2) 3/2 Mz EIz = d 2w dx 2
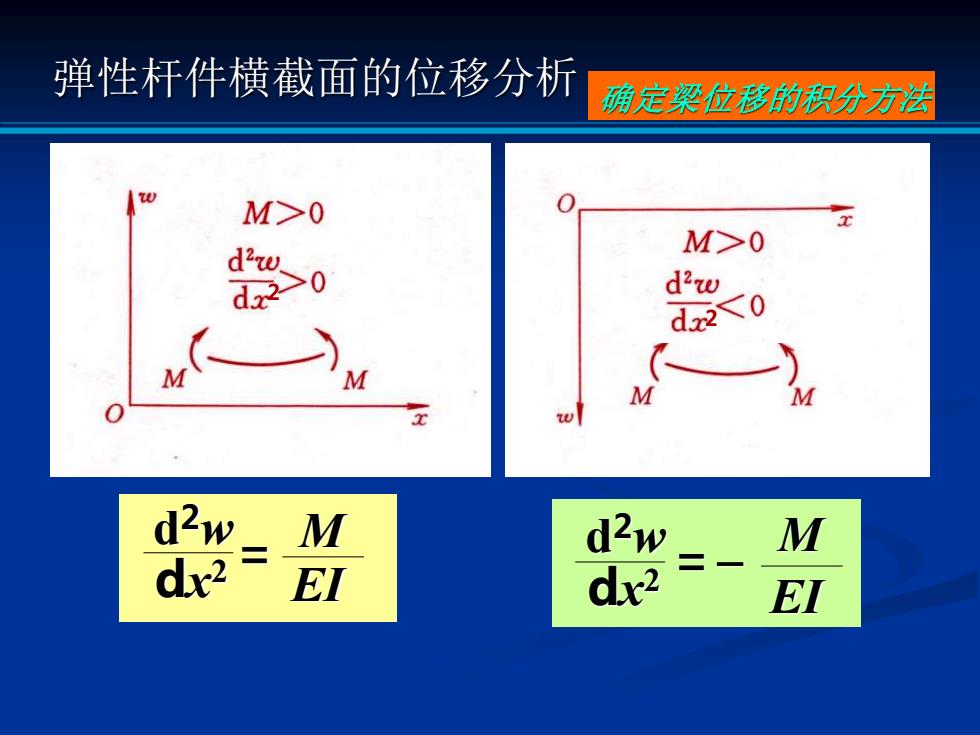
弹性杆件横截面的位移分析 确定梁位移的积分方法 M>0 d'w M>0 d2w d<0 M M M M d2w M d2w M dx2 EI dx2 EI
确定梁位移的积分方法 M EI = d 2w dx 2 d = 2w dx 2 M EI − 2 2 弹性杆件横截面的位移分析

第13章 弹性杆件横截面的位移分析 确定梁位移的积分方法 0(x)= dw(x) dx EI=El.y=[JM(x)dxdbx+Cx+D
确定梁位移的积分方法 第13章 弹性杆件横截面的位移分析 = = EI = M x dx +C dx dy EI dx dw EIZ z z ( ) EIZ w = EIz y = M x dxdx+Cx + D ( ) dx C EI M x dx dw x x = = + ( ) ( ) ( ) dxdx Cx D EI M x w x = + + ( ) ( )

例:悬臂梁受力如图所示.求梁的转角方程和 挠度方程,并确定最大转角0和最大挠度w 解:1.弯矩方程 M(x)=-P(-x) 2.微分方程和积分 图7-5 d2w P (1-x) 积分法举例 dx2 EI 3.支座边界条件定常数 0x)= 1-x)2+C 0(0)=0,C= PP 2EI 2EI w(x)= (I-x)3+Cx+D PP 6EI w(0)=0, D=- 6EI
例:悬臂梁受力如图所示.求梁的转角方程和 挠度方程,并确定最大转角θ和最大挠度w EI Pl w D 6 (0) 0, 3 l x Cx D = = − EI P w x = − + + 3 ( ) 6 ( ) 积 分 法 举 例 1 解:1.弯矩方程 2.微分方程和积分 3.支座边界条件定常数 ( ) 2 2 l x EI P dx d w = − l x C EI P x = − − + 2 ( ) 2 ( ) EI Pl C 2 (0) 0, 2 = =

于是该梁的转角方程和挠度方程分别为 P P12 0(x)= (1-x)2+ 2EI 2EI w(x)= P -x)3+ P12 PL 6EI 2EI 6EI 积分法举例 求得 88=8()= 12 ,印19l= E1 W=W0= 即IWLx= pl3 3E1
积分法举例1