
第七章拉压杆的强度与变形
第七章 拉压杆的强度与变形
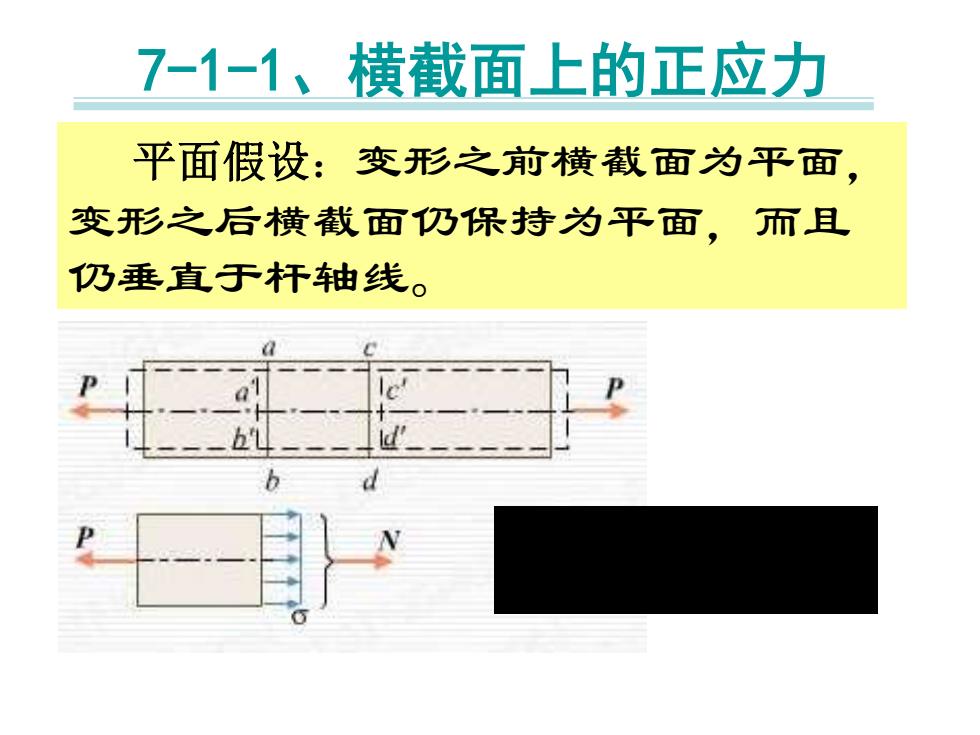
7-1-1、横截面上的正应力 平面假设:变形之前横截面为平面, 变形之后横截面仍保持为平面,而且 仍垂直于杆轴线
7-1-1、横截面上的正应力 平面假设:变形之前横截面为平面, 变形之后横截面仍保持为平面,而且 仍垂直于杆轴线。 = = A FN dA A

正应力 法向应ヵNormal Stress 正应力公式: Normal stress 正应力的 正负号规定为: 拉应力为正, 压应力为负
正应力 法向应力 Normal Stress •正应力公式: Normal stress A FN = 正应力的 正负号规定为: 拉应力为正, 压应力为负
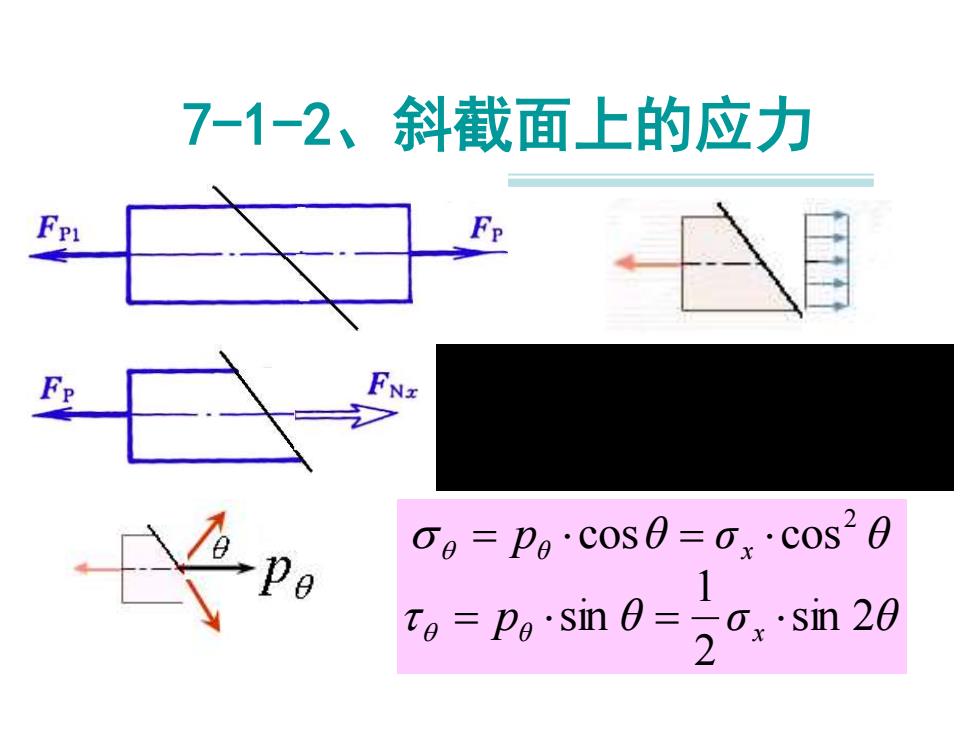
7-1-2、斜截面上的应力 Fp -po 0,=pg·C0s0=ox·cos20 To=Po'sin 0=1 0x·sin20
7-1-2、斜截面上的应力 σ θ θ A F A F p x Nx θ Nx cos cos = = = p θ σ θ p θ σ θ θ x θ x sin 2 2 1 sin cos cos2 = = = =
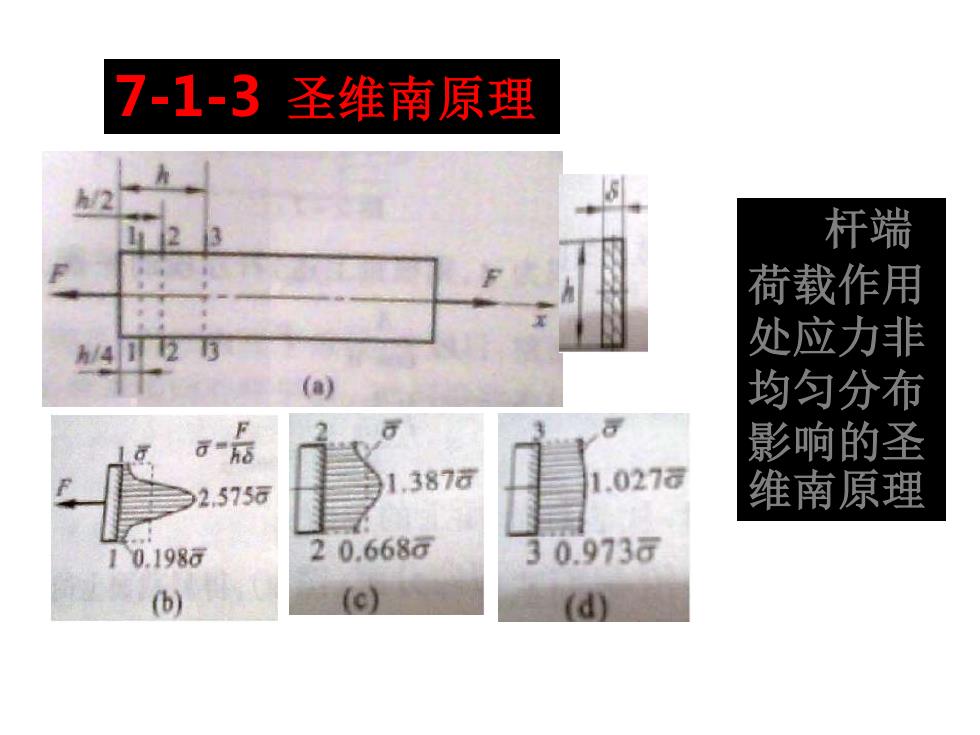
7-1-3圣维南原理 /2 1山1213 杆端 荷载作用 /42万 处应力非 (a 均匀分布 F 影响的圣 387a 2.5756 027 维南原理 10.1986 20.668a 3 0.973a (b) d
7 - 1 - 3 圣维南原理 杆端 荷载作用 处应力非 均匀分布 影响的圣 维南原理
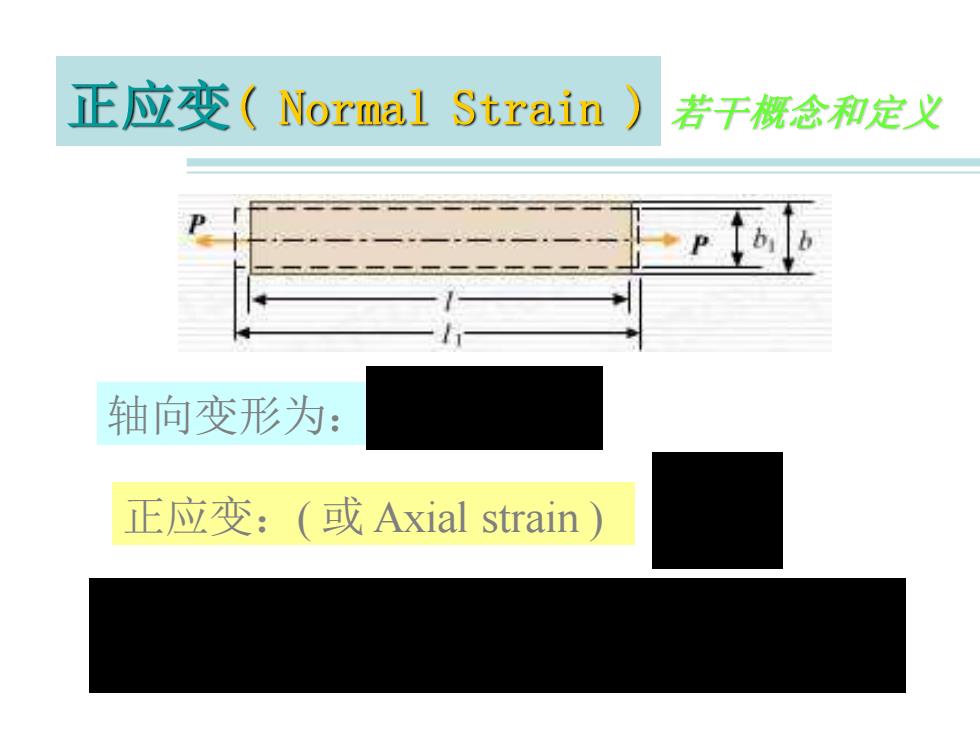
正应变(Normal Strain) 若干概念和定义 轴向变形为: 正应变:(或Axial strain)
正应变( Normal Strain ) 若干概念和定义 轴向变形为: 正应变:( 或 Axial strain ) 正应变 的正负号规定为:拉应变为正, 压应变为负。 l = l −l 1 l l =
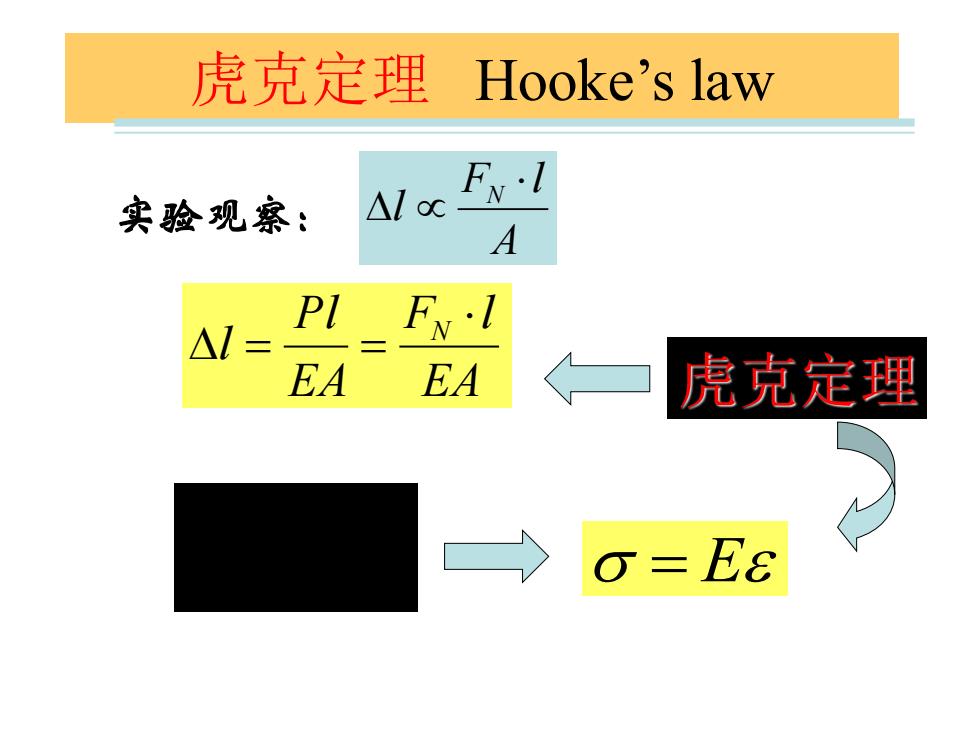
虎克定理 Hooke's law Fw·l 实验观察: △loc A △l= Pl FxI EA EA 虎克定理 o=E8
虎克定理 Hooke’s law A F l l N 实验观察: EA 虎克定理 F l EA Pl l N = = l l E A FN = = E
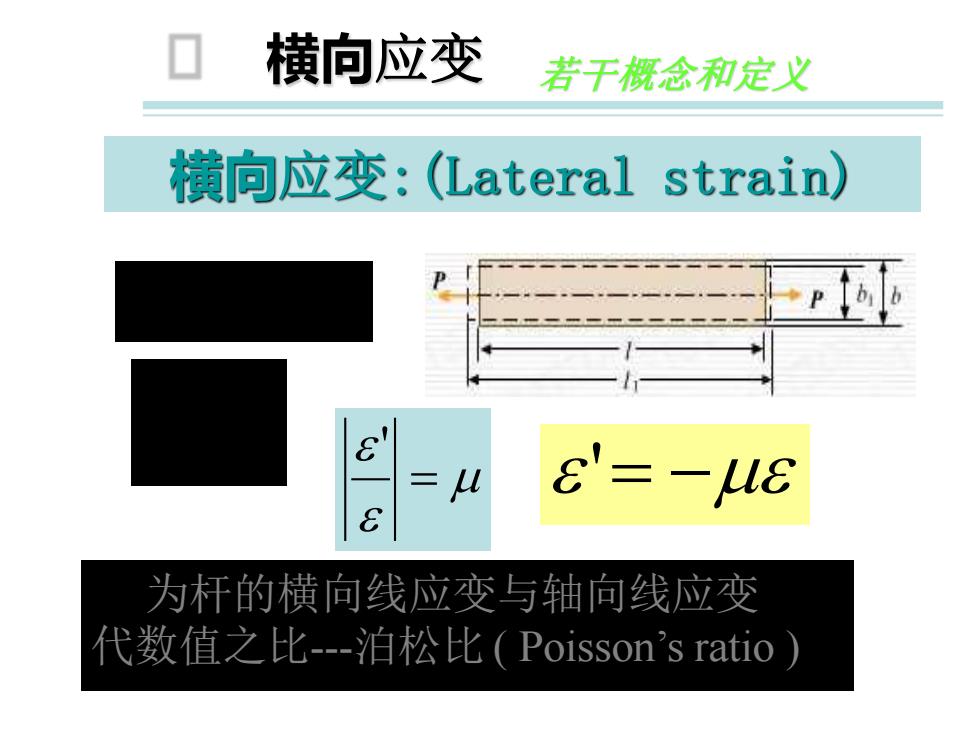
横向应变 若干概念和定义 横向应变:(Lateral strain) 8'=-U8 为杆的横向线应变与轴向线应变 代数值之比-泊松比(Poisson's ratio)
横向应变:(Lateral strain) 横向应变 若干概念和定义 为杆的横向线应变与轴向线应变 代数值之比-泊松比 ( Poisson’s ratio ) b = b1 −b b b ' = = ' ' = −
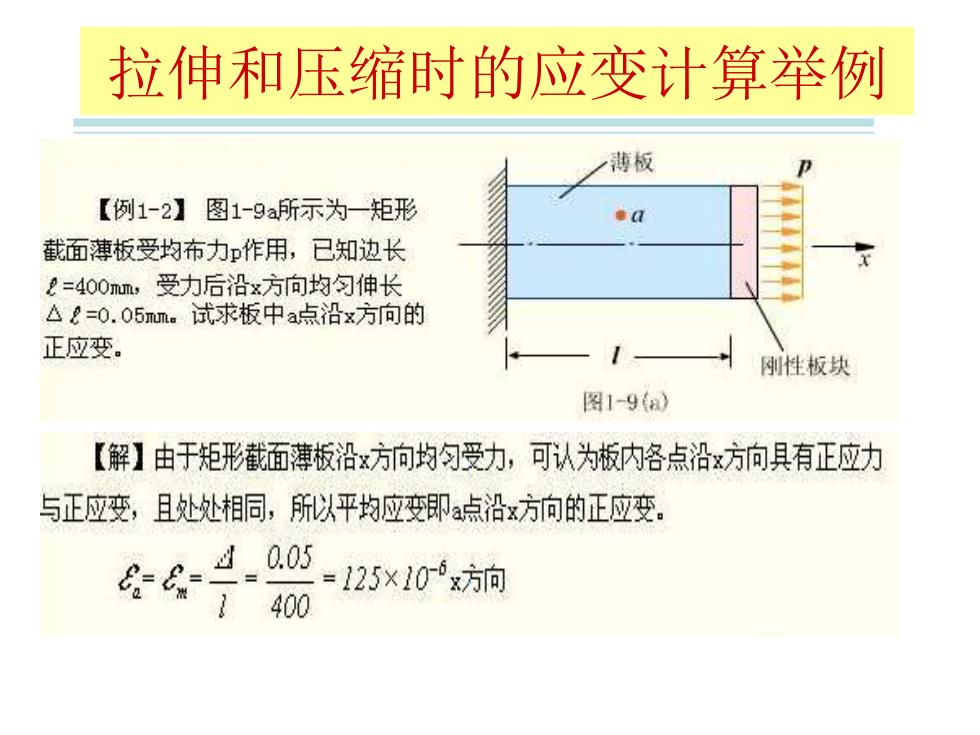
拉伸和压缩时的应变计算举例 薄板 【例1-2】图1-9a所示为-矩形 d 截面薄板受均布力p作用,已知边长 l=400mum,受力后沿x方向均匀伸长 △2=0.05mum。试求板中a点沿x方向的 正应变。 刚性板块 图19a) 【解】由于矩形截面薄板沿x方向均匀受力,可认为板内各点沿x方向具有正应力 与正应变,且处处相同,所以平均应变即点沿x方向的正应变。 4 05=125×10x方向
拉伸和压缩时的应变计算举例
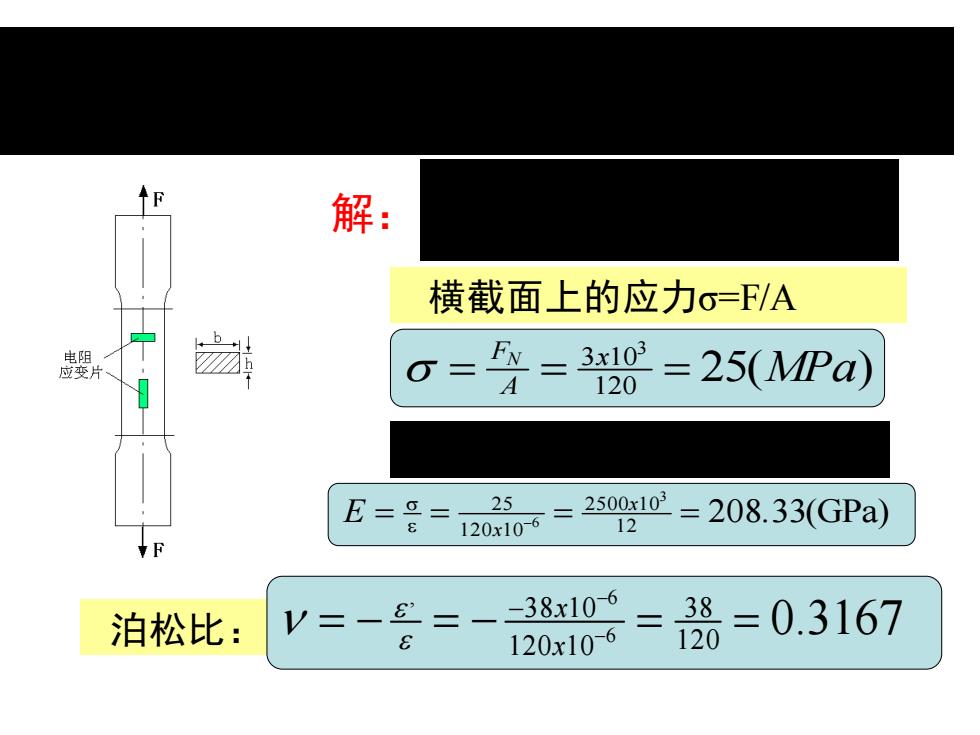
解: 横截面上的应力o=F/A o==30=25(wPa) 120 E=g=12 25 120x10-6 2s00x10=208.33(GPa) 12 泊松比: V=-£=-38x106 120x10-6 38 120 =0.3167
例4:一板状试样如图,已知:b=4mm,h=30mm,当施加 F=3kN的拉力时,测的试样的轴向线应变ε=120x10-6 ,横向线应 变ε’=-38x10-6;试求试样材料的弹性模量E和泊松比ν 解: 求试件的轴力FN=F=3kN; 横截面面积A=bh=120mm2 , 横截面上的应力σ=F/A 25( ) 120 3 103 MPa x A FN = = = 根据胡克定律σ=Eε得: 泊松比: 0.3167 120 3 8 120 1 0 3 8 1 0 6 , 6 = − = − − = = − − x x 208 33(GPa) 1 2 2500 1 0 120 1 0 2 5 3 6 E . x x = = − = =