
动量矩定理 与 动量矩守恒律
大学 物理 动量矩定理 与 动量矩守恒律

质点组的动量定理 设质点组由i个质点组成,其中任一质点P,的 质量设为m,它对惯性参照系坐标原点O的位矢 为,作用在质点P上诸力的合力为F,对质 点组而言,该合力又分为合内力F①及合外力)。 P 应用牛顿第二定律,质点 有运动微分方程 d=e)+0 m;d (i=1,2,.,n)
大学 物理 一 质点组的动量定理 设质点组由 个质点组成,其中任一质点 的 质量设为 ,它对惯性参照系坐标原点 的位矢 为 ,作用在质点 上诸力的合力为 ,对质 点组而言,该合力又分为合内力 及合外力 。 应用牛顿第二定律,质点 有运动微分方程 i Pi mi O i r Pi Fi (e) Fi (i) Fi ( 1,2, , ) ( ) ( ) 2 2 F F i n dt d r m i i e i i i = + = Pi
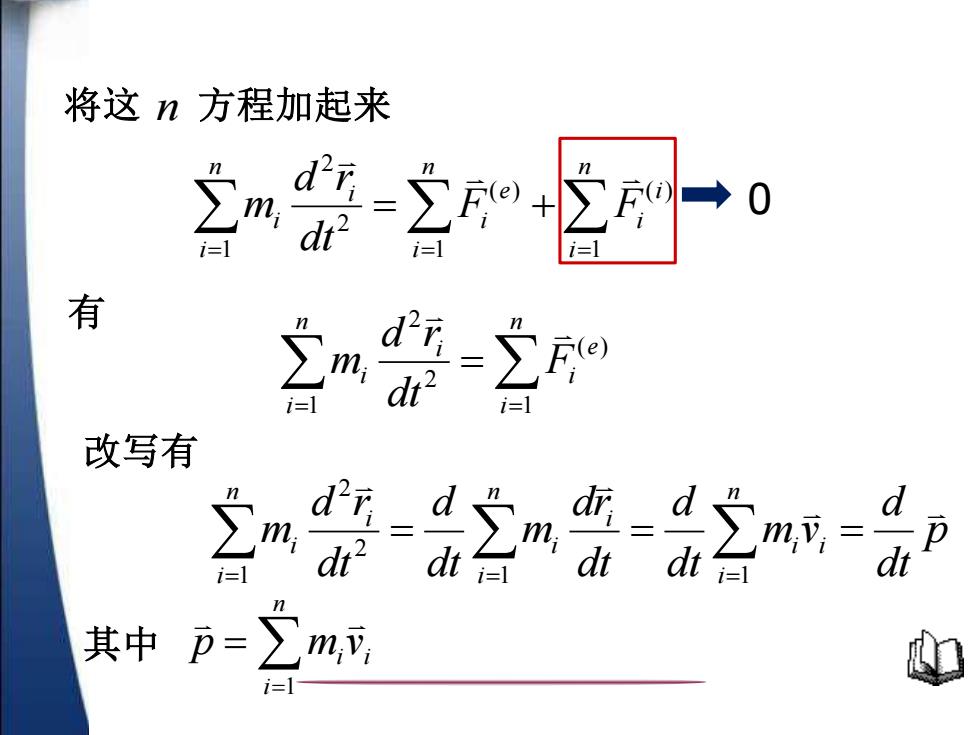
将这n方程加起来 有 d= n m i=1 改写有 di= d t台 其中p=∑m可
大学 物理 将这 n 方程加起来 = = = = + n i i i n i e i n i i i F F dt d r m 1 ( ) 1 ( ) 1 2 2 0 = = = n i e i n i i i F dt d r m 1 ( ) 1 2 2 有 p dt d m v dt d dt dr m dt d dt d r m n i i i n i i i n i i i = = = =1 =1 =1 2 2 改写有 其中 = = n i i i p m v 1

可得 所-立,英巾n-公m →质点组的动量定理 如
大学 物理 可得 = = n i e Fi dt dp 1 ( ) ,其中 = = n i i i p m v 1 质点组的动量定理

二质心运动定理 由质点组的动量定理 因为 ∑m可=m。 d 得mdi n nma,=∑e-或 d。 Fe) dt i=l
大学 物理 二 质心运动定理 = = = n i e i n i mi vi F dt d 1 ( ) 1 由质点组的动量定理 因为 c n i i i m v mv = =1 = = n i e c Fi mv dt d 1 ( ) 得 = = n i e c Fi v dt d m 1 ( ) ( ) 1 ( ) e i n i e mac Fi F = = = 或 = = n i e i c F dt d r m 1 ( ) 2 2 c v

三质点组的动量守恒定律 若∑F=0→面=0→D=0 dt p=mvc 可。=恒矢 质心运动守恒定律 若∑Fe=0 若c=恒矢 烟花的质心轨迹
大学 物理 三 质点组的动量守恒定律 若 0 ( ) e F = 0 dt dp p = 0 c p mv = vc = 恒矢 质心运动守恒定律 若 0 ( ) e Fx 若 vxc = 恒矢 烟花的质心轨迹

动量矩定理 与 动量矩守恒定律 如
大学 物理 动量矩定理 与 动量矩守恒定律

(1)对某一固定点0的动量矩定理 M 其中J=∑c×p,)M=∑c,×Ee)。 0
大学 物理 (1)对某一固定点O 的动量矩定理 M J = dt d 其中 = = n i i i 1 J (r p ) , = = n i e i i 1 ( ) M (r F )
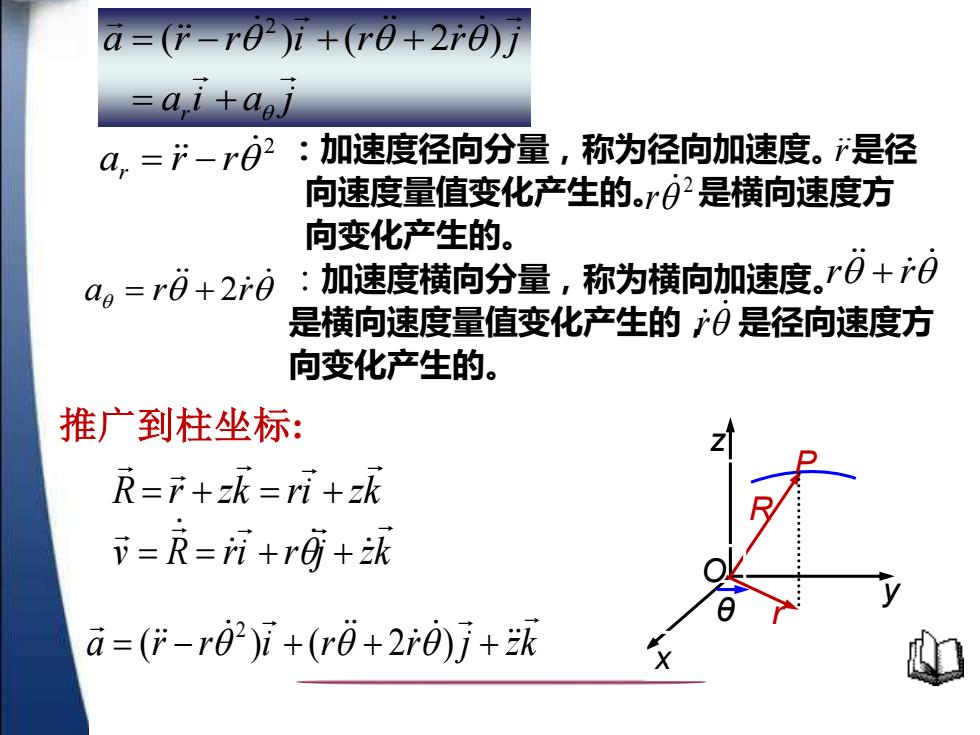
a=(r-r02)i+(r0+2r0)J =ai+aoj 4,=产-r02:加速度径向分量,称为径向加速度。是径 向速度量值变化产生的。r0是横向速度方 向变化产生的。 a。=ri+2r0:加速度横向分量,称为横向加速度。r0+r0 是横向速度量值变化产生的广0是径向速度方 向变化产生的。 推广到柱坐标: R=r+zk=ri+zk =R=i+rG+讯 ā=(-r0)i+(r0+2r0)j+
大学 物理 :加速度横向分量,称为横向加速度。 是横向速度量值变化产生的, 是径向速度方 向变化产生的。 推广到柱坐标: y x z P O r R θ :加速度径向分量,称为径向加速度。 是径 向速度量值变化产生的。 是横向速度方 向变化产生的。 r a i a j a r r i r r j r = + = ( − ) + ( + 2 ) 2 r + r r R r zk ri zk = + = + v R ri r j zk = = + + a r r i r r j zk = ( − ) + ( + 2 ) + 2 2 a r r r = − a = r + 2r 2 r

(2)动量矩守恒律 当外力对固定点O的合力矩为零时,有 dJ =M=0 dt J=恒矢量 宇恒律还适于仅在某一轴上投影的情形
大学 物理 (2)动量矩守恒律 当外力对固定点O的合力矩为零时,有 = M = 0 J dt d J = 恒矢量 守恒律还适于仅在某一轴上投影的情形