
非惯性系动力学(二)
非惯性系动力学(二)
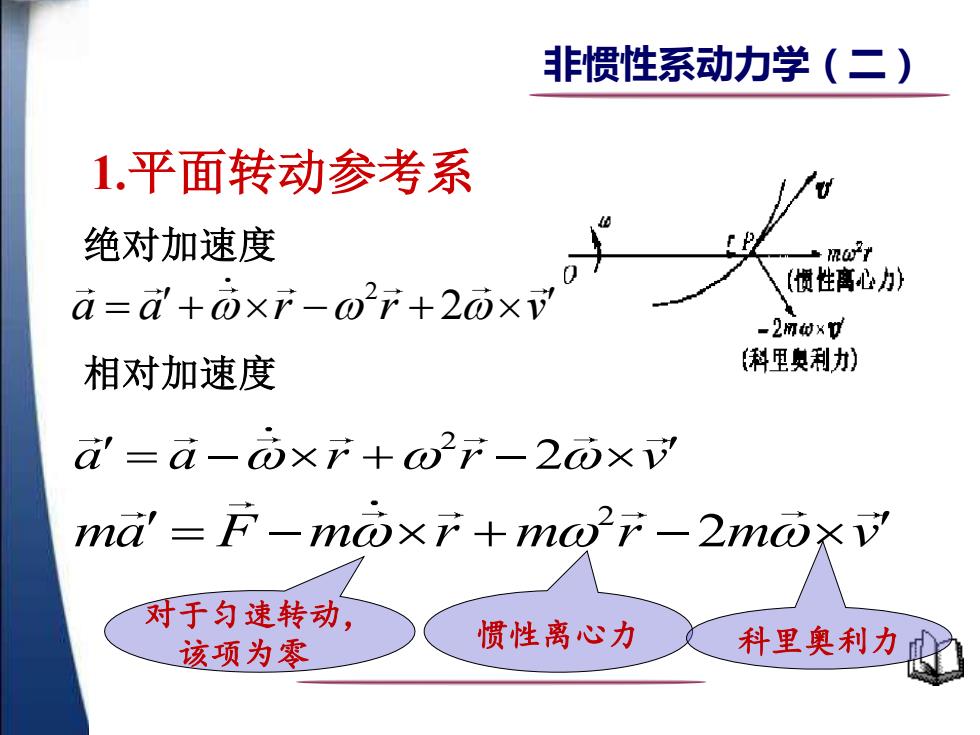
非惯性系动力学(二) 1.平面转动参考系 绝对加速度 mary d=d+ò×r-or+2ox oX1 惯性离心) -2M的xv 相对加速度 科里奥利) =a-ò×r+w2r-2而× md=F-o×产+mwF-2m⑦XV 对于匀速转动, 该项为零 惯性离心力 科里奥利力
大学 物理非惯性系动力学(二) 2 ma F m r m r m v = − + − 2 对于匀速转动, 该项为零 惯性离心力 科里奥利力 2 a a r r v = + − + 2 绝对加速度 2 a a r r v = − + − 2 相对加速度 1.平面转动参考系

非惯性系动力学(二) 例在一光滑水平直管中,有一质量为m的小球, 此管以恒定角速度ω绕通过管子一端的竖直轴转 动。如果起始时,球距转动轴的距离为a,球相 对于管子的速度为零,求小球沿管的运动规律及 管对小球的约束反作用力
大学 物理非惯性系动力学(二) 例 在一光滑水平直管中,有一质量为m的小球, 此管以恒定角速度ω绕通过管子一端的竖直轴转 动。如果起始时,球距转动轴的距离为a,球相 对于管子的速度为零,求小球沿管的运动规律及 管对小球的约束反作用力
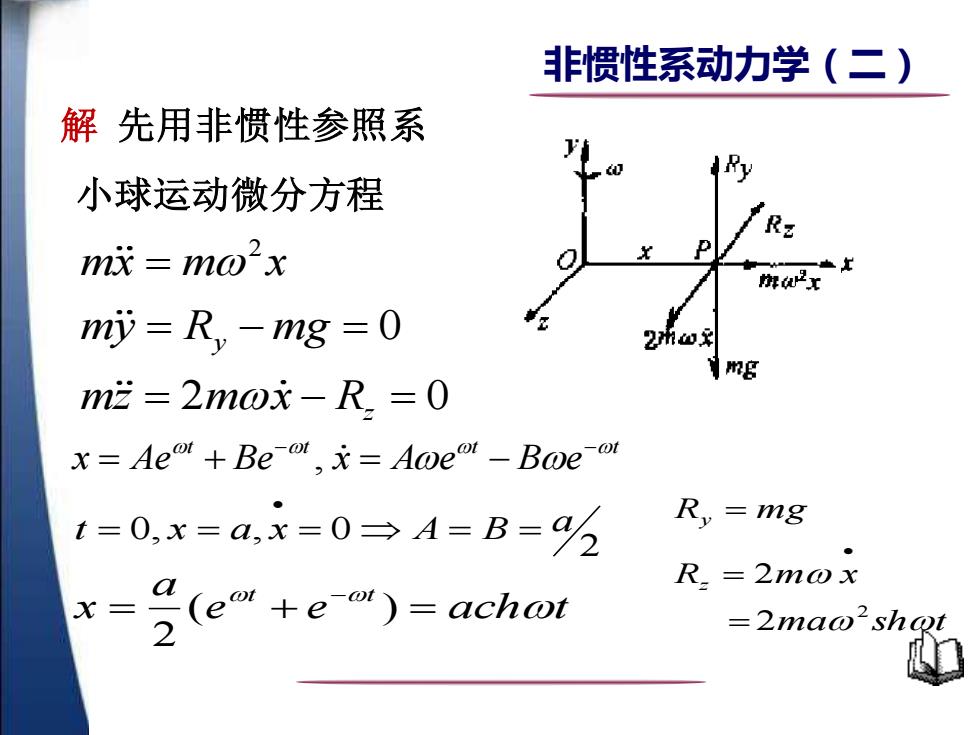
非惯性系动力学(二) 解先用非惯性参照系 小球运动微分方程 m成=mo2x mi=R,-mg =0 mi=2mox-R.=0 x=Ae+Be o,Aoeu-Boe ou t=0,x=a,x=0→A=B=% Ry=mg ● x=. (e+)-acho R.=2mox =2mao'shot
大学 物理非惯性系动力学(二) 解 先用非惯性参照系 小球运动微分方程 2 0 2 0 y z mx m x my R mg mz m x R = = − = = − = , t t t t x Ae Be x A e B e − − = + = − e e ach t a x t t = + = − ( ) 2 2 t = 0, x = a, x = 0 A = B = a • ma sh t R m x R mg z y 2 2 2 = = = •

非惯性系动力学(二) 改用惯性参照系,选极坐标系 运动微分方程 D m(-r02)=F,=0 m(r0+2r0)=R。 (极轴) 0=0=常数,0=0 mi=ro2 mx=mox 2mr@Ro 比较 mi=2mox-R.=0 如用柱坐标,可求出方向的反作用力
大学 物理非惯性系动力学(二) 改用惯性参照系,选极坐标系 运动微分方程 ( ) ( ) 2 0 2 m r r Fr m r r R − = = + = = = = 常数, 0 2 2 mr r mr R = = 2 2 0 z mx m x mz m x R = = − = 比较 如用柱坐标,可求出z方向的反作用力。

非惯性系动力学(二) 2.空间转动参考系 B a='+d,+d。 d,=0x产+0(0)-o分 =0xr-02R d=2⑦× 图4.2.1 md'=F+mw2R-2mo×v md=F-m+mo2R-2mo×
大学 物理非惯性系动力学(二) ( ) 2 2 t a r r r r R = + − = − 2 ma F m R m v = + − 2 2 0 ma F ma m R m v = − + − 2 a v c = 2 t c a a a a = + + 2.空间转动参考系

非惯性系动力学(二) 如
大学 物理非惯性系动力学(二)