
省级精品课程——材料力学 第二章轴向拉伸和压缩 §2.1轴向拉伸和压缩的概念及实例 工程结构中,承受轴向拉伸或压缩的杆件是很多的,例如组成起重机构架的 杆件,组成屋架的杆件等,如图2-1所示。上述结构在只承受结点载荷的情况下, 都可以简化为析架,各结点都可以简化为铰,各杆均可以简化为二力杆。这些杆 件的受力特点是外力的作用线与杆的轴线重合,其变形特点是沿轴线方向伸长或 宿短,横成面作对平行移动,如1一2所述。 (a) (b) 2- 本章主要研究轴向拉伸或压缩杆件的强度和刚度计算,并逐步介绍材料力学 的一些基本概念和基本方法。 2.2轴向拉(压)杆的内力 一、外力与内力的概念 对于我们的研究对象,例如一个物体或物体的一部分来说,其他物体或物 的其他部分对于研究对象的作用就是该对象的外力。例如研究屋架,屋面的重量 就是屋架的外力,又称载荷:屋架支座的反力也是层架的外力。若研究屋架中的 某一根杆,则屋架的其他部分对该杆的作用就是该杆的外力。在考虑构件的自重 时,自重也是该构件的外力 构件在外力作用下,由于它的各部分之间相对位置改变而引起的相互作用力 就是内力。因此内力与构件的变形密不可分,研究强度、刚度 稳定性问题必 研究内力。我们知道,即使不受外力作用构件的各部分之间仍然存在内力,以保 持为一个整体。我们不研究这种内力。构件在外力作用下的内力称为附加内力, 简称内力,材料力学就是研究附加内力。 由连续性假设知,内力是分布力,存在于受力构件的每一点处。 二、求内力的方法:截面法 由于内力是构件内部各部分之间的相互作用力,它总是成对出现。在投影方 程中,任何一对内力的投影总是等于零 为了研究内力,我们必须让它显示出来 并能将任一对内力中的一个分离出来,这就是所谓截面法,它是材料力学 一个 基本法。 8 This document is generated by trial version of Print2Flash(www.printflash.com)

省领精品课程 一材料力学 现以图2-2(a)为例说明截面法。该杆在A、B两端及C截面处共有三个外 力作用。现求C段中的一m截面上的内力。其步骤如下: 1.假想地用截面在mm处将杆切为两部 ,双 分: 2.选取其中任一部分作为研究对象,也 就是取分离体。图2-2(b)就是选取mm截 面以右的那一部分杆作为分离体。 卧 +x( 3.抛弃另一部分。被抛弃的部分对分离 体的作用以内力代替,如图2-2(b)所示 M 的内力N。稍加思考便可知,对于图2-2 →x(C) (b)的分离体来说, 已经是它的外力 日2x 了。我们通过以上工作,已经把杆在一” 截面上的内力转化为分离体上的外力,因 oP 而显示出来了。 4.建立分离体上力的平衡条件,确定未 图22 知的内力。ACB杆在三个外力作用下处于 平衡状态,它的任何一部分应处于平衡状态,故可对分离体应用力的平衡方 程,图2-2为共线力系,对分离体由ΣX=0得。 N-2P=0 N,=2P(拉) 综上所述,截面法的要点可归纳为以下五个字:切、取、代、平衡。截而法 的实质就是将内力转化为外力并显示出来,然后计算。 这个例子还说明,虽然内力是分布力,但用截面法求出的只是这个分布力的 合力,如图2-2(b)所示。因此,我们取分离体时,可以不用图2-2(b),而直 接采用图22(c)。以后,我们说某个截面上的内力,通常就是指该截面上分布 内力的合力。 由图2-2(b)或(c)看到,内力N,的作用线与杆的轴线重合。我们把轴向拉 (压)杆的内力称为轴力。 同理,可由截面法求得CB段中n截面上的内力心,=-P(压),相应分离体 见图2-2(d)。 三、轴力符号 当分离体选择不同,或未知内力假定的方向不 同,所得到的内力可能有不同的符号为了统一,我 们规定按变形选取轴力的正负号,即在某截面附近 取一小段杆,若为拉伸变形,则该截面轴力N取正 取伤 图2-3 。变 形选取轴力 的符号正是内力与变形密不可分关系的反映。 四、轴力图 一般地说,不同的截面处轴力不同。也就是,轴力N是截面位置x的函数。 在N-x坐标系所描绘的函数图线就是轴力图,见图2-2()。轴力图形象地表示 This document is generated by trial version of Print2Flash(www.print2flash.com)

省级精品课程 材料力学 了拉(压)杆的变形。图2-2(e)表示,该杆AC段为拉伸变形,拉力为2P;CB 段为压缩变形,压力为P。 例2-1:图示为上端悬挂的钢缆,已知钢缆的容重为Y,横截面积为A,长 为L。求钢缆的内力 A (0) (b) (d) 例2-1图 解:作用在缆绳上的外力是绳的自重和上端的约束反力,自重是沿杆长均匀分布 的外力。 用截面体求任意截面m的内力N,分离体见图(b),由分离体上力平衡条件得: N-YAx=0 N=YAx 因Y和A均为常量,故内力为N是x的线性函数。N的变化可用轴力图()来 表示。在截面法中,构件被设想截面切为两部分后,可选取其中的任一部分 作为分离体。木题也可选mm截面以上部分作为分离体,见图(c)。 §2.3轴向拉(压)杆横截面上的应力 、应力的概念 在相同材料的情况下,判断一根拉或压杆的危险程度,不仅要考虑其轴力的 大小,还要考虑该杆的粗细,也就是,应当考虑每单位截面上的轴力。如果内力 在截而上分布不均匀,则还要考虑内力在截面的每一点处分布的密集程度,由此 我们引入应力的概念。 为了表示构件的某个截面上任意一点C处的内力分布密集程度(简称集度), 可围绕C A,设△A上内力的合力为 △P,则比值△P/△A称为 微面积△A上的平均应力。当△A→0时得△P/AA的极限值p: AP兰贵 (2-1) p称为C点处的总应力。为便于分析问题,我们把微面积△A上的内力△P 在C点的法线方向和切线方向分解,得法向分量△N和切向分量△T,见图2-5(a)。 同样道理得极限值。 公 This document is generated by trial version of Print2Flash(www.printflash.com)

省领精品课程—材料力学 。=一岩兴 (2-2) (2-3) 是和:分捌称为C点处的正应力和明应力,见图256.上述三种应力的关系 DG1r (2-4) 国25 离开截面的正应力称为拉应力,指向截面的正应力称为压应力。我们规定 正应力以拉取正号,以压取负号,见图2-6(a)。还规定,剪应力以其矢量有 0-580-s0 g1Ta回9 国2-6 绕截面内侧任一点作顺时针旋转的趋势取正号,反之取负号,见图2-6(b)。 应力的量纲是[力]/[长度].常用国际单位是N/m,称为帕,记作Pa。10N/m 10N/ 10°N/m分别称为千帕, 兆帕 ,吉怕、记作KPa、MPa、GPa 二、拉(压)杆横截面上的正应力 要确定拉(压)杆横截面上任意一点的应力,首先要弄清内力在该截面上的 分布规律。而力是不容易观察的,比较容易观察的是变形,因此我们可以通过观 察杆的变形规律来推测内力的分布规律。我们见到的弹簧称就是这方面的例子, 用弹簧称重实际上看到的是弹簧的变形,但表面上是将变形量换算成重量 实验研究拉(压)杆的变形 加力前在杆的表面上画横向线1-1和2-2,纵向线1-2,3-4,5-6,见图2 ()。加力后,横向线发生平移。由原米位置变到1·-1’和2·-2‘:纵向线 变形的程度都相同,变形后的横向线与 纵向线仍然垂直。根据材料的连续性和 均性,可由老及里推测截面上名甘 也发生了与横向线相同的位移, 即变形 后的横截面发生了平移,仍为垂直于轴 (b) 线的平面,这就是所谓平面假定。根据 图27 平面假定,拉(压)杆两横截面之间的 所有纵向线段的变形程度都相同,且与横截面垂直。 由变形规律推测应分布规律。 变形不 超过 定限度时,由变形与力的关系可知,使各纵向线段变形的内 力都相同,也就是横截面上的各点的应力都相同,进一步研究还表明,正应力σ This document is generated by trial version of Print2Flash(www.print2flash.com)

省领精品课程 材料力学 与线段的伸长或缩短变形有关,剪应力π与直角的改变有关。纵向线段与横截面 间的直角不变。故横截面上没有剪应力,而只有正应力。。 由平衡条件确定应力的大小。 由截面法求出的内力实际上是横截面上内力的合力,因此有 N=∫adM=o∫dA=oA 所以 6= (2-5) 这就是拉(压)杆横截面上正应力计算公式,式中N是轴力,A是横截面积。 例2-2:计算例2-1中钢缆的最大正应力。已知Y=76.9KN/m,1=100m。 解:因为杆的横截面积A为常数,故最大正应力发生在轴力最大的横截面 即上端悬挂处的截面。由图2-4(d), N..=YAl §2-4轴向拉(压)杆斜截面上的应力 为了研究轴向拉(压)杆的各种破坏现象,必须弄清不同截面上的应力。研 究方法与上 节类似。见图2-8( 在杆的表面画平行斜线1 一些纵向线段,由表面变形推知内部变形,再由变形推知应力分布。前面己说过, 所有纵向线段的变形程度相同,因而可推知斜面上的各点的应力P,相同,见图 ( 图2-8 2-8(b)。再由平衡条件得到 N=P.Aa 这里A,为斜截面积,A=A/cos,代入上式得到 (2-6) 为便于应用,将总应力P分解为正应力o,和剪应力x,由图2-8(c)知, a=Pa cosa=o cosia (2-7) =P,sin a sin 2a (2-8) 公 This document is generated by trial version of Print2Flash(www.print2flash.com)

省级精品课程—材料力学 由以上三式可以看到,P。、。、t均为α的函数,也就是说,不同的截面 上应力不同。最大应力对我们很有用 当a=0时,6s=g,t。=0 即最大正应力发生在横截面上,O=。,该截面上的剪应力为零。 当a=45时,lrm=20,a。= 即最大剪应力发生在与轴线成45°的斜面,?=20,该斜面上的正应力也 等于横截而上的正应力的一半。 §2.5轴向拉(压)杆的强度计算 首先建立两个概念:工作应力和容许应力。构件在载荷作用下产生的应力称 为工作应力。实际工程中,为了保证构件能正常地工作,即不发生破坏,对不同 材料的各类构件的工作应力都规定了一个容许的值,称为这材料的容许应力。容 许应力是在实验的基础上规定的。容许正应力记为[。]。 这样,构件能正常工作,即不发生破坏的条件是:构件内最大工作应力不得 超过材料的容许应力。对于拉(压)杆这个条件是: A ≤ (2-9) (2-9)式称为拉(压)杆的强度条件 应用强度条件(29》 可以解决以下三类强度计算问题 1.强度校核已知杆的尺寸、载荷以及材料的容许应力,验算杆件是否满 足强度要求。 2.设计截面已知载荷及材料的容许应力,确定杆的最小横截面积。即 3.确定容许载荷已知杆的横截面积和材料的容许应力,确定容许载荷。 即 Ns≤[o]A 例2-3:有一高度1=24m的方形截面等直石柱,截面边长为1.5m,其顶部受轴 向载荷P-1000KN作用,见图2-9(a)。已知材料的容重Y=23KN/m,容许应力 [o]=1MPa,试校核石柱的强度。 解:首先计算石柱的轴力,图2-9(b)就是分离体,由分离体的平衡条件 得。 N=-(P+YAx)(压力) This document is generated by trial version of Print2Flash(www.print2flash.com)
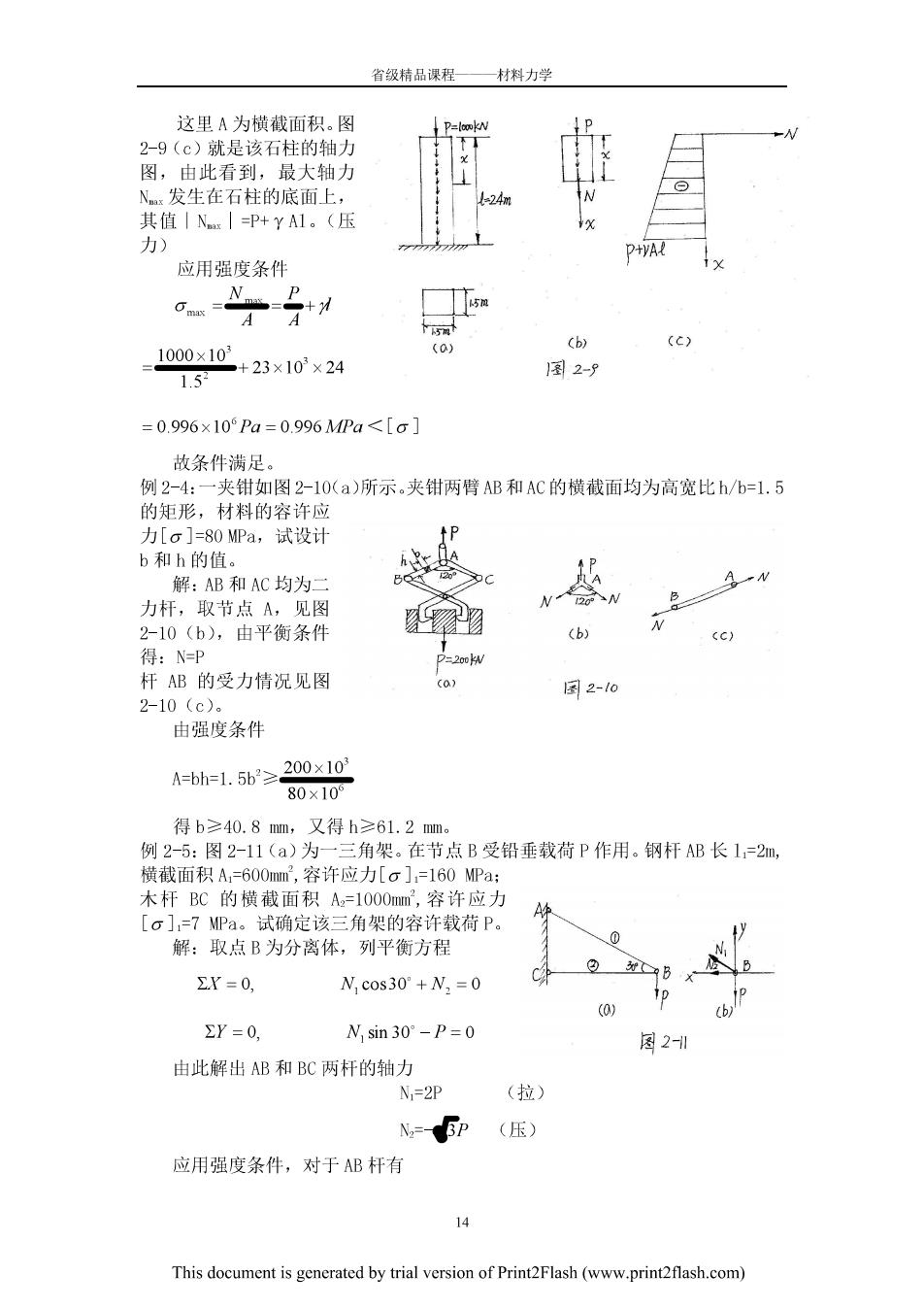
省领精品课程 一材料力学 这里A为横截面积。图 2-9(c)就是该石柱的轴力 图,由此看到, 最大轴力 发生在石柱的底面上, 其值|N|=P+YA1。(压 力) 应用强度条件 1000×10+23×103×24 (b) 1图2-9 152 =0.996×10Pa=0.996MPa<[c] 故条件满足。 例2-4:一夹钳如图2-l0(a)所示.夹钳两臂AB和AC的横截面均为高宽比h/b=1.5 的矩形,材料的容许应 力[g]=80MPa,试设计 b和h的值。 解:AB和AC均为 一水 力杆,取节点A,见图 B 2-10(b),由平衡条件 (b) (c) 得:N=P 杆AB的受力情况见图 o 国2-10 2-10(c》 由强度条件 A=bh=1.5b≥200x10 80×10° 得b≥40.8m,又得h≥61.2m 例2-5:图2-11(a)为 角架 。在节点B受铅垂载荷P作用。钢杆AB长1,=2m 横截面积A:=600mm,容许应力[c]=l60MPa: 木杆BC的横截面积A=1000mm’,容许应力 [o]=7MPa。试确定该三角架的容许载荷P。 解:取点B为分离体,列平衡方程 =0, B Ncos30°+V=0 (0) p 6 Y=0, N1sin30°-P=0 图21 由此解出AB和BC两杆的轴力 N,=2P (拉》 N=3p (压) 应用强度条件,对于AB杆有 This document is generated by trial version of Print2Flash(www.printflash.com)

省级精品课程—材料力学 有600x10≤160X10 2P 所以P≤48×103N 对于BC杆有 BP 700x10≤7X10 所以P≤40.4X10N 故三角架的容许截荷可取P=40.4KN。 §2.6应力均匀分布的适用条件、应力集中的概念 一、圣维南原理 工程实际问题里,外力可以通过各种方式作用于杆上。图2-12所示为同样 的拉杆,上端的受力方式不同,但这些力都是静力等效的。圣维原理指出,力作 用于杆端方式的不同,只会使与杆端距离不大于杆的横向尺寸范围内的应力受到 影响。在图2-12中,只在图示虚线范围内也就是在力作用的局部,各杆的应力 分布不同, 在离开杆端局部范围之外,应力都是 ,而按(2-5 ) 计算横批 面上的正应力,应力均匀 分布,而可以不考虑力的作 用方式。 p 圆2-2 二、应力集中的概念 根据实际需要,右要在构件上钻相,开抽等,文就引起件错截面尺十的 突然改变。这样的杆在轴向拉(压)时,在截面突然变化的部位横截面上的正应 力不再均匀分布,应力局部增大,而离开该部位稍远的地方应力又趋于均匀。这 种由于截面尺寸突然改变而引起应力局部增大的现象称为应力集中,见图2-13 (a)、(b)、(c),应力集中的程度有理论应力集中系数,表示: = (2-10) 式中σ为1-1截面上的最大应力,σ为该截面上的平均应力。构件在拉压、 公 This document is generated by trial version of Print2Flash(www.print2flash.com)
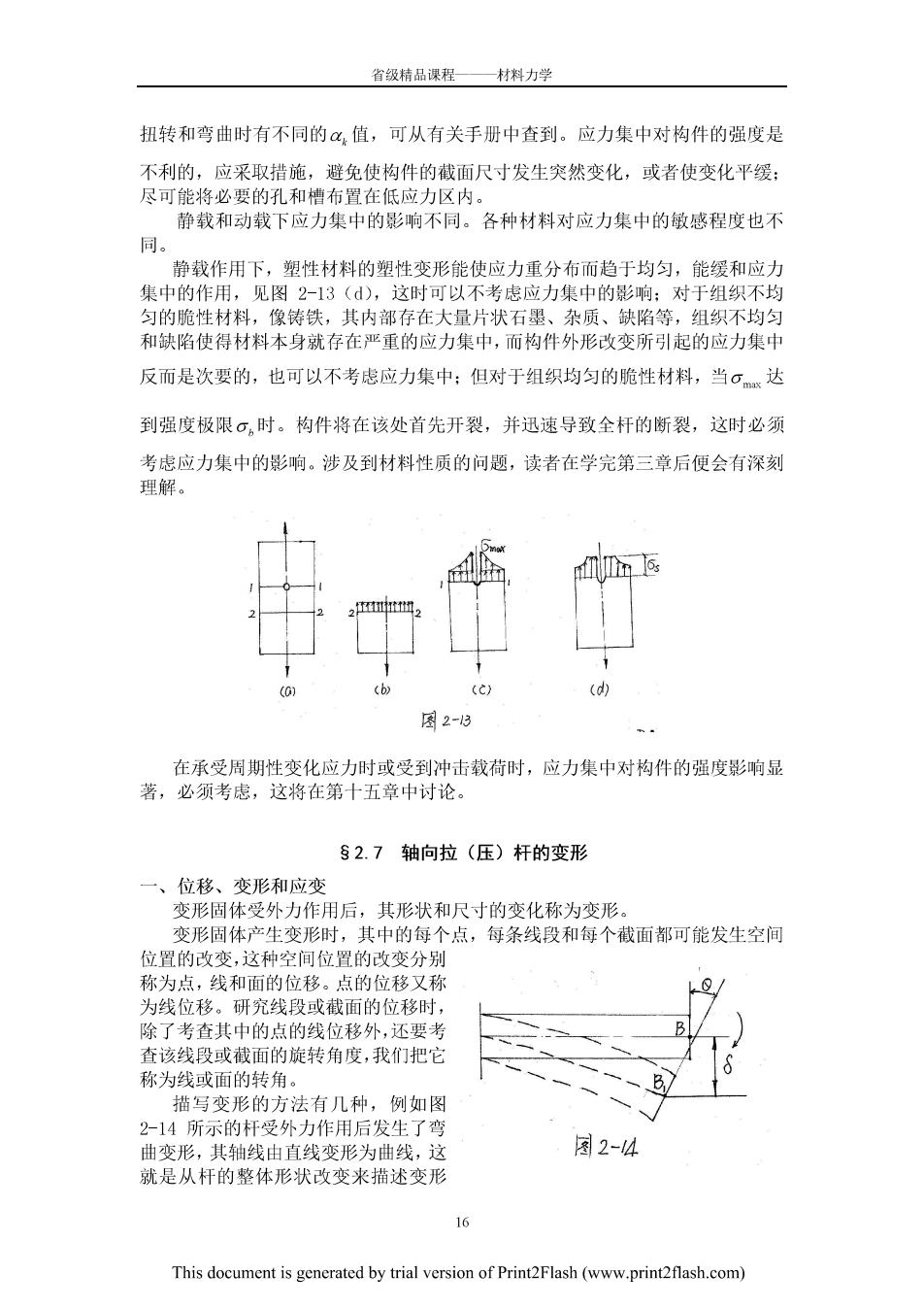
省级精品课程 材料力学 扭转和弯曲时有不同的x,值,可从有关手册中查到。应力集中对构件的强度是 不利的,应采取措施,避免使构件的截面尺寸发生突然变化,或者使变化平缓 尽可能将必要的孔和槽布置 低应力区内 静载和动载下应力集中的影响不同。各种材料对应力集中的敏感程度也不 同。 静载作用下,塑性材料的塑性变形能使应力重分布而趋于均匀,能缓和应力 住中的作用,见图2-13(d).这计可可以不考虑应力典中的号影响:对干组织不均 匀的脆性材料,像铸铁,其内部存在大量片状石墨、杂质、缺陷等,组织不均匀 和缺陷使得材料本身就存在严重的应力集中,而构件外形改变所引起的应力集中 反而是次要的,也可以不考虑应力集中:但对于组织均匀的脆性材料,当。达 到强度极限。,时。构件将在该处首先开裂,并迅速导致全杆的断裂,这时必须 考虑应力集中的影响。涉及到材料性质的问题,读者在学完第三章后便会有深刻 理解。 ( 图2-3 在承受周期性变化应力时或受到冲击载荷时,应力集中对构件的强度影响显 著,必须考虑,这将在第十五章中讨论。 §2.7轴向拉(压)杆的变形 一、位移、变形和应变 变形固体受外力作用后,其形状和尺寸的变化称为变形。 变形固体产生变形时,其中的每个点,每条线段和每个截面都可能发生空间 位程的改变,这种空间位程的改变分别 称为点,线和面的位移。 点的位移又称 为线位移。研究线段或截面的位移时 除了考查其中的点的线位移外,还要考 查该线段或截面的旋转角度,我们把它 称为线或面的转角。 描写变形的方法有几种,例如图 2-14所示的杆受外力作用后发生了弯 曲变形,其轴线由直线变形为曲线,这 园2-4 就是从杆的整体形状改变来描述变形 This document is generated by trial version of Print2Flash(www.printflash.com)

省领精品课程—材料力学 的,§1-2所讲的杆的基本变形式就是这样 1 》折的。其实,若给出B载面的转角日和卫 截面形心的垂直位移6,则图2-14所示杆 95ta5 D16 的弯曲变化也就得到控制,利用控制点的位 038 来描写杆的变形也是一种方法。还有一种方 (b) 法,如果将构件的任意局部变形弄清楚了, (0) 则整个构件的变形也就解决了。局部变形的 图2-5 描写方法是对于构件内任意 占0.首先 0占的任意微线段的伸长或缩短的程度,如图2-15(a)所示,设线段0B 变形的后的位置是OB1,伸长量是△S,则称 oB=im、 (2-11) 为0点沿0B方向的线应变,它表示了0点沿B方向的相对伸长或缩短。其次 再研究过0点的任意直角的改变。如图2-15(b)所示,设直角∠CD变形后为 ∠C,0D,则 Ya=lim((oD-∠CO,D) (2-12) 称为0点在C0D平面上的角应变。有了线应变和角应变,我们总可以把一点附近 的局部变形完全表示清楚,至于如何表示我们将根据具体问题逐步学习。 二、拉(压)杆的纵向变形 由验得到拉(压)轩的纵向您形规独,拉伸时纵向伸长,压缩村纵向培短 当材料不超过弹性范围内时,其伸长或缩短量△与轴力N和杆长1成正比,与 横截面积A成反比,即 4/=M (2-13) FA 式中E为比例常数,称为材料的弹性模量,是一个材料常数。由(2-13)式看到,EA 越大则△W越小,EA称为拉(压)杆的刚度 纵接移4山=- 横向镀彩4d=dd -16 因为。=N1A,拉(压)杆的变形是均匀的,故任一点的纵向应变可用平 均值表示,即ε=△1,代入(2-13)式并路去下标得到 6=或o=EE (2-14) 我们把(2-13)和(2-14)式都称为虎克定律,它们是两种不同形式,前者 表示杆的总伸长或缩短量与轴力之关系,后者表示任一点附近的应变和应力之关 系。 三、拉(压)杆的横向变形 This document is generated by trial version of Print2Flash(www.print2flash.com)