
省级精品课程一材料力学 第六章截面的几何性质 在学习了轴向拉(压)、剪切和扭转等杆的基本变形形式后,下面将学习弯曲变形。前 面已看到,对杆的每一种基本形式,我们要研究应力(强度)和变形(刚度)问题。而这些 问题中,又离不开要分析截面的内力和几何性质。由于弯曲问题的内容较多,从这一章开始 至第九章,我们将弯曲问题分为几何性质、内力、应力和变形四个部分来讨论。 另一方面,到弯曲变形为止,我们将光成杆的基本变形的学习。因此,从这一章至第九 章的学习中,我们还要穿插进基本变形的有关内容的总结, §6.1形心和面积矩 杆的截面就是一个平面图形。平面图形的几何中心称为该图形的形心。例如圆心就是圆 的形心,形心是一个纯几何量。但是,若将平面图形看作是厚度可无限小的均南薄板,则该 薄板的重心就是图形的形心 平面图形(截面)对坐标轴y和z的面积矩分别由下列两个积分来定义(图6-1) 图6-1 S,=∫d4 6) S,=∫d 若将微面积dA看作是微小力6A,将整个截面积A看作是合力pA,这里6为板厚 而P为材料的容重,则由合力矩定理可得到形心坐标与面积矩的关系: ∫2dA=2.A 6-2) ∫dA=yA 当截面面积A已知时,利用(6-2)式可解决两类问题:第一,已知形心坐标z:和y。,求面积 矩S,和S:第二,己知面积矩S,和S,求形心坐标, This document is generated by trial version of Print2Flash(www.printflash.com)
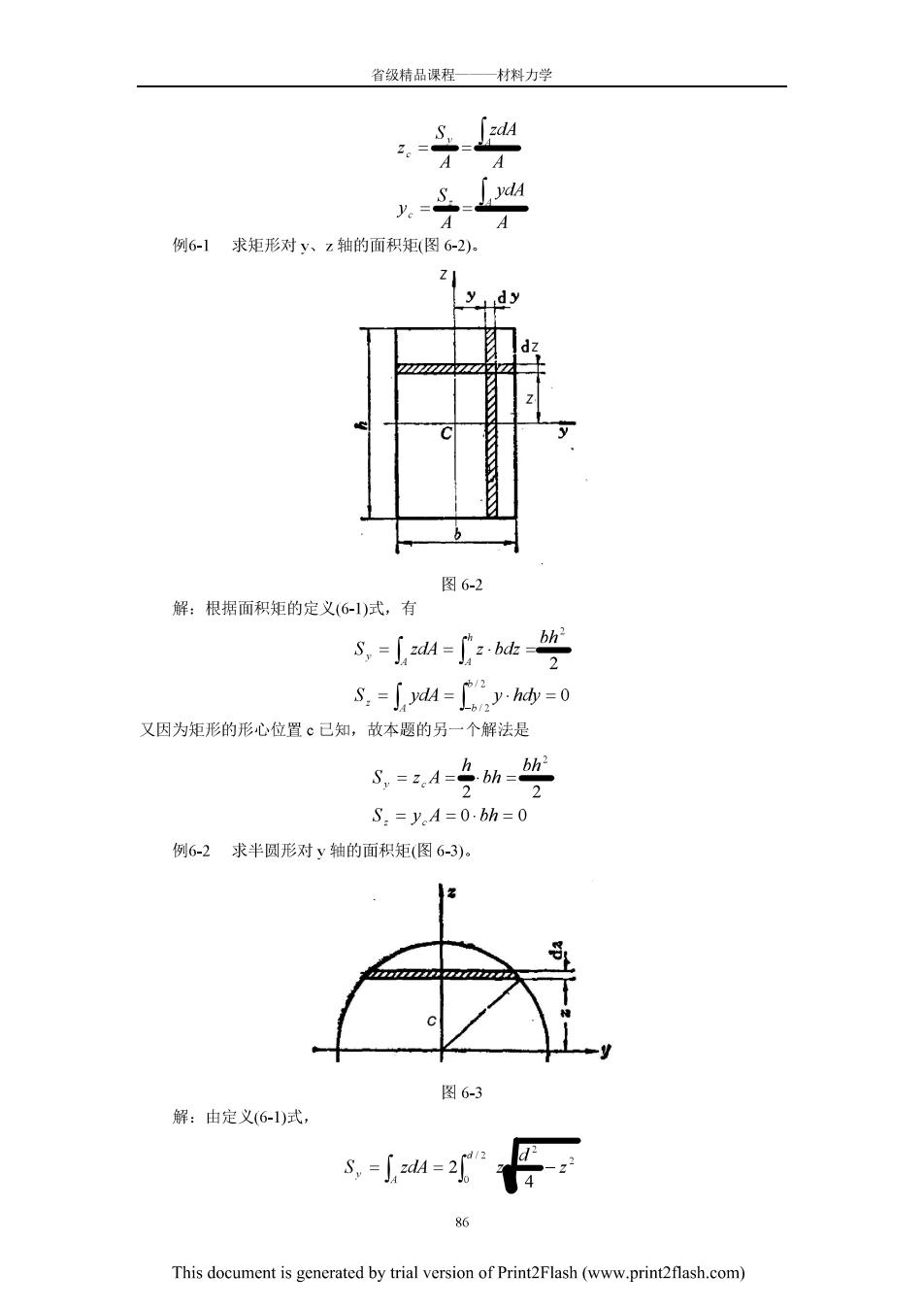
省领精品课程—材料力学 :.-S. A 例6-1求矩形对y、z轴的面积矩(图6-2)。 y dy 图62 解:根据面积矩的定义(6-1)式,有 8=小能空 S.=[dA=心2yhd=0 又因为矩形的形心位置©已知,故本题的另一个解法是 8=4专的空 S:=yA=0.bh=0 例6-2求半圆形对y轴的面积矩(图6-3) 图6-3 解:由定义(6-1)式, s,=fd=2 This document is generated by trial version of Print2Flash(www.print2flash.com)

省级精品课程 一材料力学 12 讨论:利用本题结果,可进一步求出半圆的形心位置。由于图形对称,形心c在乙轴上。 例6-3求图6-4所示对称T形截面的形心位置。 200 30 200 -30 图6-4 解:工程上一些复杂的截面图形,常可看作是由几个简单图形组合而成。将一个复杂图 形分解为几个简单图形可避免像(61)那样的积分运算而用求和来代替。 第一步,将T形分解为两个矩形。 第二步,利用简单图形的形心位置己知,求面积矩。取参考坐标如图64。 S,=200×30×100+200×30×215=1.89×10°mm3 面积矩的量纲是长度的三次方。同一个截面对不同轴的面积矩是不同的,其值可能为正 可能为负,也可能为零。由(6-2)式可看到,若某轴通过图形之形心,则图形对该轴之面积矩 为零:反之,若图形对某轴的面积矩为零,则该轴一定通过图形之形心。这是一条很有用的 性质。 §6.2惯性矩、惯性积、极惯性矩和形心主惯性矩 一.惯性矩、惯性积和极惯性矩 参看图6-1,一个平面图形对y轴的惯性矩是 1,=∫z2dA (6-3) 平面图形对y轴的惯性矩是 This document is generated by trial version of Print2Flash(www.printflash.com)
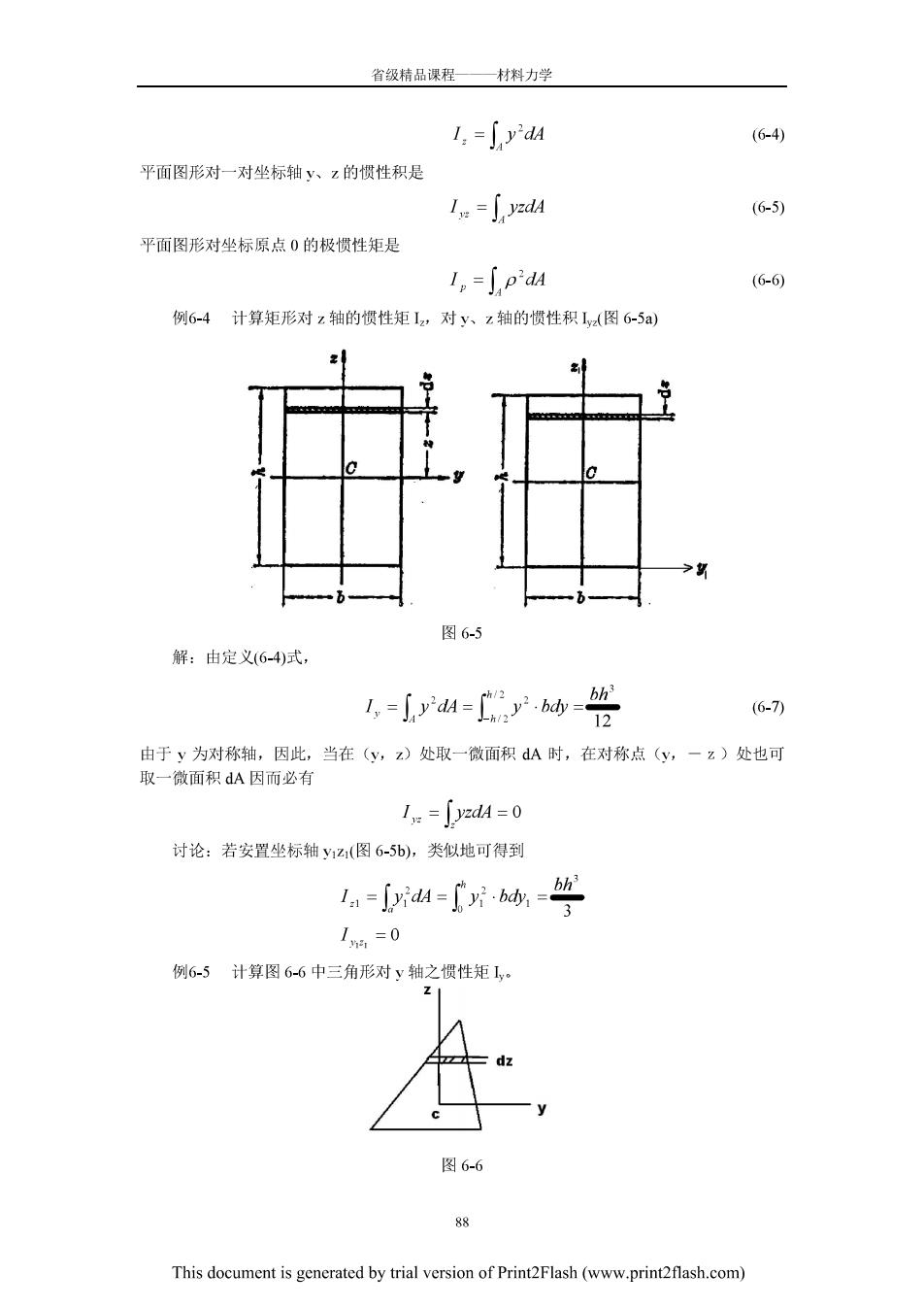
省领精品课程一材料力学 1,=∫y'da (6-4) 平面图形对一对坐标轴y八、z的惯性积是 I.=∫zdM (6-5) 平面图形对坐标原点0的极惯性矩是 1。=pdM (6-) 例6-4计算矩形对z轴的惯性矩l2,对y、z轴的惯性积,图6-5a) 图6-5 解:由定义6-4)式, 1==产侣 6-7) 由于y为对称轴,因此,当在(y,z)处取一微面积A时,在对称点(y,一z)处也可 取一微面积dA因而必有 Iv=[yzd4=0 讨论:若安置坐标轴y2(图6-5b,类似地可得到 1-i4=r-空 1=0 例65计算图6-6中三角形对y轴之惯性矩1 图6-6 This document is generated by trial version of Print2Flash(www.print2flash.com)

省级精品课程——材料力学 解:由定义(6-3)式, 1,a4:eh-k纸 (6-8 例6-6计算圆形对通过圆心轴的惯性矩1,和1以图6-7). 图6-7 解:因为任何一个过圆心的轴都是圆的对称轴,所以1,1。根据极惯性矩之定义(66) 式,有 1。=∫pdA=∫02+zHa =1+1, 利用第五章所得到的圆形的极惯性矩(5-10)式, 32 于是 1=, (6-9) 同一截面对不同坐标轴的惯性矩或惯性积不同。惯性矩和惯性积的量纲为长度的四次 方。惯性矩、极惯性矩恒等正值。惯性积的值可能为正,可能为负,也可能为零。 二.形心主惯性轴和形心主惯性矩 通过某一点,可以作很多坐标系,图形对这些坐标系的惯性积可能为正,可能为负,也 可能为零。若图形对于某一对坐标轴的惯性积为罗,这一对轴就称为主惯性轴,简称主轴。 例如图65b中,过0,点可以作很多对坐标轴,而y☑轴就是主惯性轴。 如果主惯性轴的坐标原点是截面形心,这时的坐标轴就称为形心主惯性轴 ,简称形心 轴。例如图6-5a中,yz轴是主惯性轴,主原点0与矩形的形心,因此z轴是形心主惯性轴。 图形对形心主惯性轴的惯性矩称为形心主惯性矩,简称形心主矩。 根据前面的分析,对于至少有一个对称轴的图形,若将该对称轴作为一个坐标轴,将形 This document is generated by trial version of Print2Flash(www.print2flash.com)
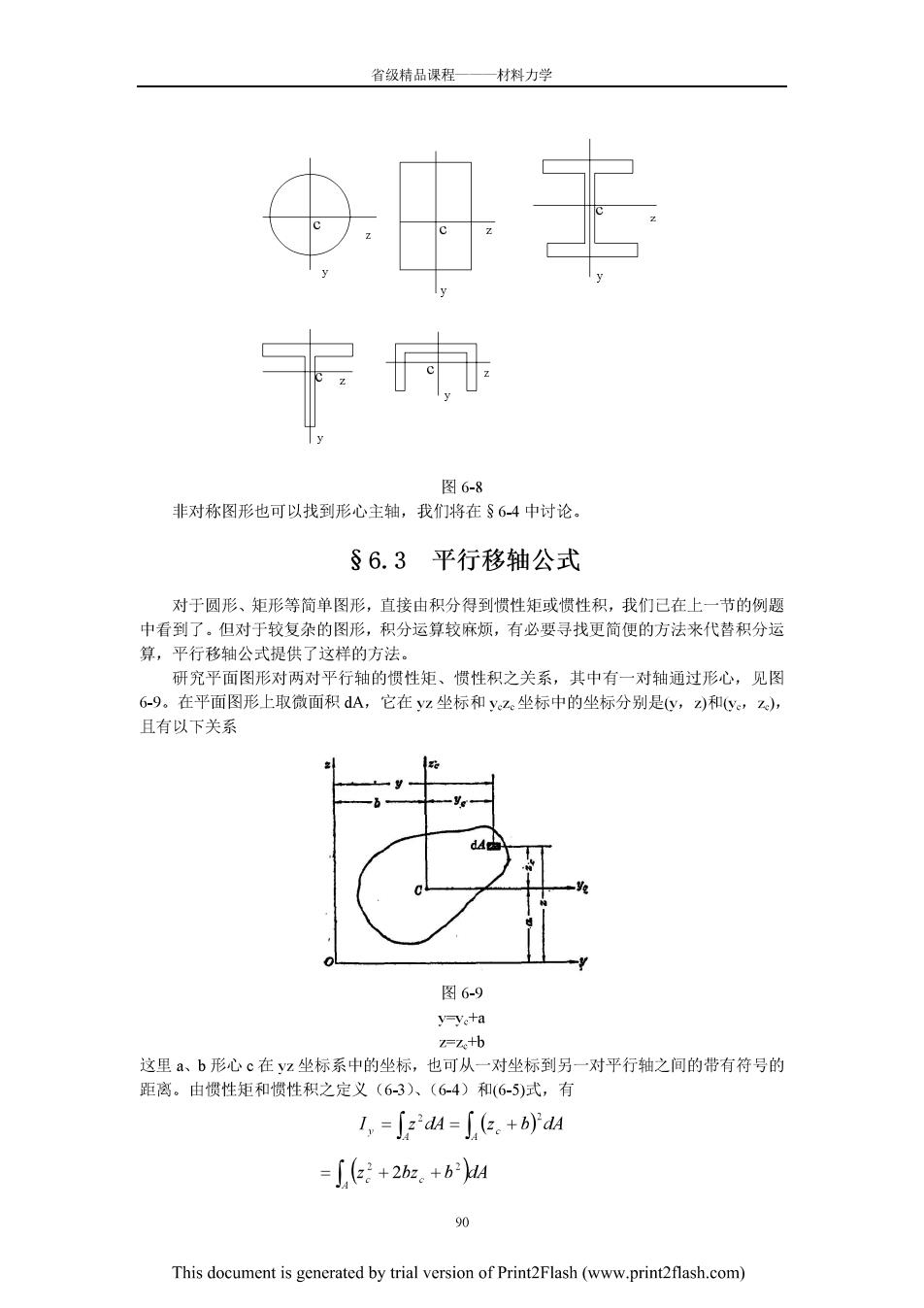
省级精品课程—材料力学 图6-8 非对称图形也可以找到形心主轴,我们将在§64中讨论。 §6.3平行移轴公式 对于圆形、矩形等荷单图形,直接由积分得到惯性矩或惯性积,我们已在上一节的例题 中看到了,但对于较复杂的图形,积分运算较麻烦,有必要寻找更简便的方法来代替积分运 算,平行移轴公式提供了这样的方法。 研究平面图形对两对平行轴的惯性矩、惯性积之关系,其中有一对轴通过形心,见图 6-9。在平面图形上取微面积dA,它在yz坐标和ye坐标中的坐标分别是y,)和(y,, 且有以下关系 图6-9 y-y+a zz+b 这里a、b形心c在z坐标系中的坐标,也可从一对坐标到另一对平行轴之间的带有符号的 距离。由惯性矩和惯性积之定义(6-3)、(64)和(6-5)式,有 1,=Sda=f(.+bda =∫:+2b.+ba This document is generated by trial version of Print2Flash(www.print2flash.com)

省级精品课程—材料力学 根据惯性矩的定义,上式第一项为l又由于y不坐标轴通形图形形心,故S,=∫z,dA=0. 而dA=A.因此 I,=Iv+biA (6-10a) 同理 1.=1n+a2A (6-10b) I =I +abA (6-10e) 例6-722a工字钢上下真缘各焊接一块钢版,其横截面如图6-10所示。 试求此组合截面的形心主惯性1。 解:此组合截面由三部分组成:工字形和两个矩形。查型钢表得工字钢 的13400cm。应用平行移轴公式,并利用矩形截面的惯性矩公式(6-7),得到组合截面的形 心主矩: -100 30 30 图6-10 图6-11 1 1,=3400+22×10x1+10x1x115 -3400+2647=6047cm 例6-8计算图6-11所示截面的形心主矩1z。 解:第一步求形心ε的位置,该截面有一个对称轴,故应决定形心的高 度。,取参考坐标如图示。将截面看作是由三个矩形组成。应用面积矩公式 (120×40+2×30×140)y=120×40×160+2×30×140×70 所以 y.=102.7mm 第二步应用平行移轴公式求↓ =120x40+120x40x573+2位0x140'+0x10×27 =(0.64+15.76+2(6.86+4.491)×10° 9 This document is generated by trial version of Print2Flash(www.printflash.com)
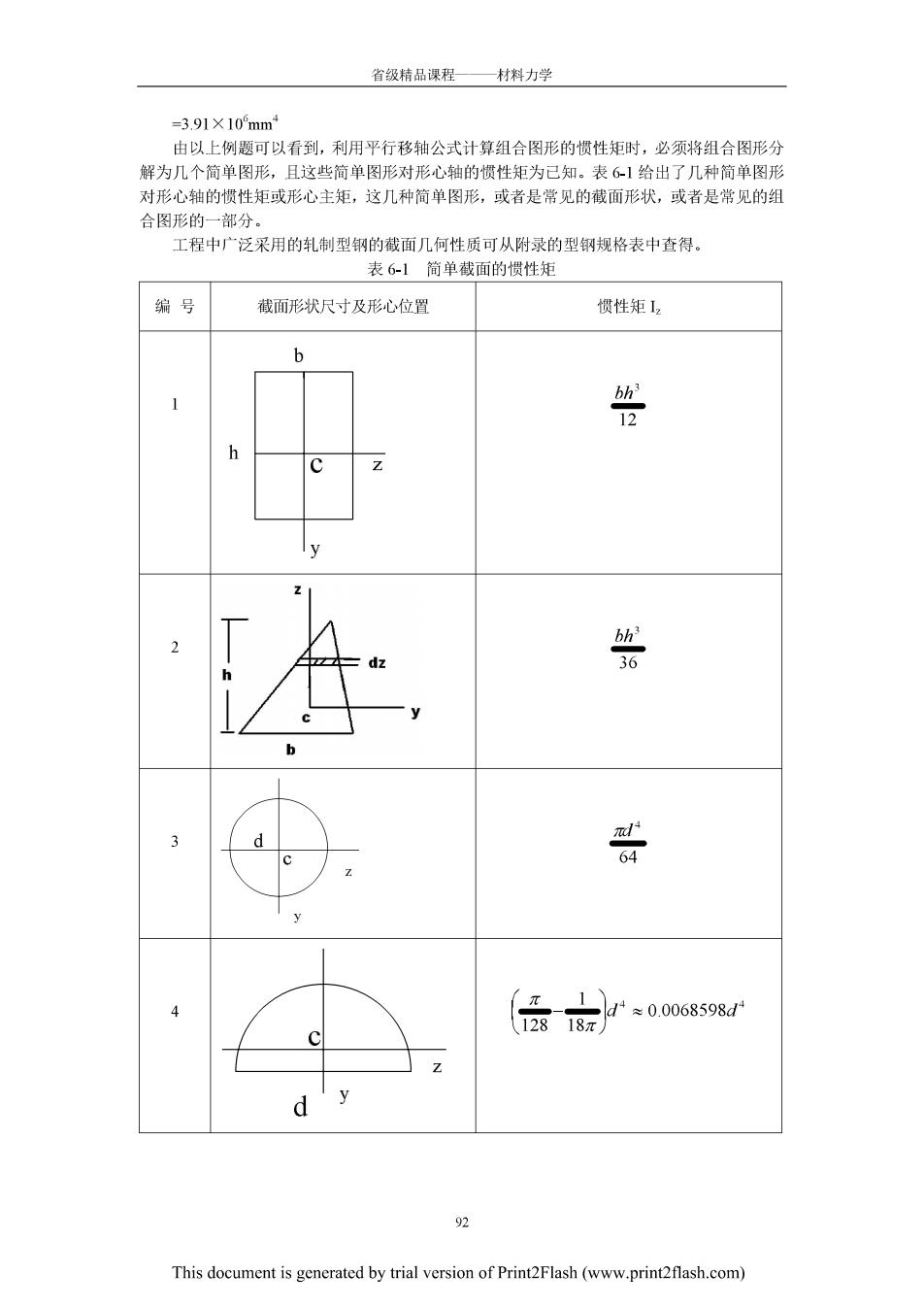
省级精品课程—材料力学 =3.91X10mm1 由以上例题可以看到,利用平行移轴公式计算组合图形的惯性钜时,必须路组合图形分 解为几个简单图形, 1这些简单图形对形心轴的惯性矩为已知。表6]给出了几种简单图形 对形心轴的惯性矩或形心主矩,这几种简单图形,或者是常见的截面形状,或者是常见的组 合图形的一部分。 工程中广泛采用的轧制型钢的截面几何性质可从附录的型钢规格表中查得。 表6-1简单截面的惯性矩 编号 截面形状尺寸及形心位置 惯性矩12 安 答 共 (债}r068s9财 This document is generated by trial version of Print2Flash(www.print2flash.com)
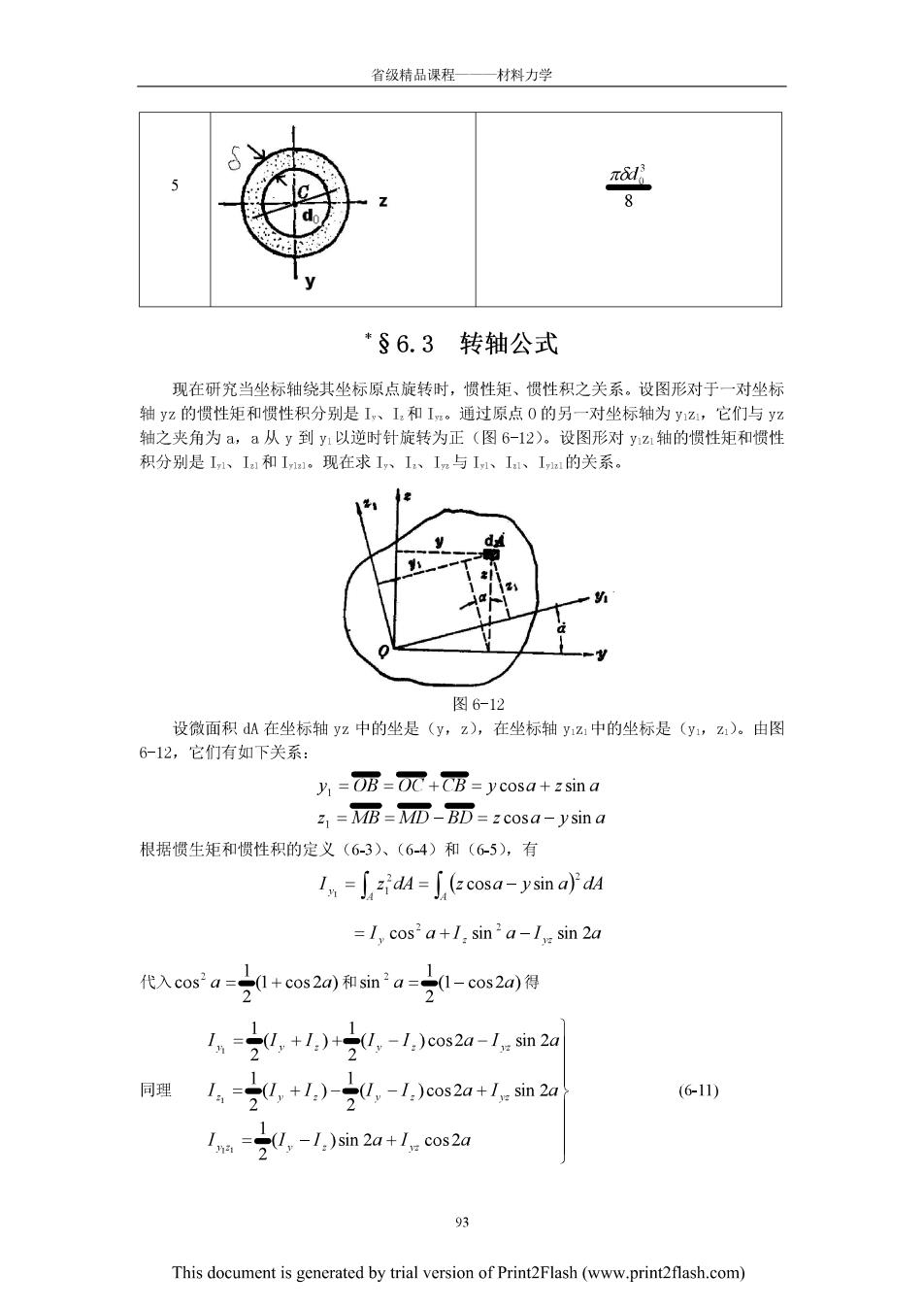
省级精品课程一材料力学 8 *§6.3转轴公式 现在研究当坐标轴绕其坐标原点旋转时,惯性矩、惯性积之关系。设图形对于一对坐标 轴yz的惯性矩和惯性积分别是1,、1,和1。通过原点0的另一对坐标轴为y2,它们与yz 轴之夹角为a,a从y到y1以逆时针旋转为正(图6-12)。设图形对y轴的惯性矩和惯性 积分别是、la和1。现在求I、n与1、1、1的关系 图6-12 设微面积dA在坐标轴yz中的坐是(y,z),在坐标轴yz中的坐标是(y,)。由图 6-12,它们有如下关系: y=0死=0元+CB=ycosa+zsma =M历=M而-m=zcosa-ysin 根据惯生矩和惯性积的定义(63)、(64)和(65),有 In=∫zdM=∫zcosa-ysin a')d4 =I,cos2a+I;sin2a-I sin 2a 代入cosa=20+cos2a和ma=20-cos2)得 1=20,+1,)+20,-1,)cos20-/m2a 同理1=20,+1,)2,-1,)os2a+1:sin20 (6-11) 1nm=20,-1,)sin2a+1.c0s2a This document is generated by trial version of Print2Flash(www.printflash.com)

省领精品课程—材料力学 这就是惯性矩和惯性积的转轴公式。 由转轴公式可知,、和z是a的函数。下面求惯性矩的极值,令 -21 g2,=7,- (6-12) 利用公式 1-1 cos2a。 0+g2a。,-1)+4明 -21 sin2a。=g2a。·c0s2a。 ,-1)+41 比较()式和(6-11)式的第三式可知,求极大极小惯性矩与求主惯性矩是一回事情。因 而图形对通过某一点的诸轴的惯性矩中的极大和极小惯性矩,也就是图形对通过该点的主轴 的主矩。对于某一点,(613)式不仅是极大和极小惯性矩公式,而且也是通过转轴找到的 主矩公式。 例6-9 求图613所示截面的形心主轴和形心主矩 25 0 -16 图6-13 解:第一步,求形心位置。选参考坐标轴z,将截面分为两个矩形,运用面积矩公式, 得 S.=(6×22+3×16y。=3×22×1.5+3×16×8 S,=(6×22+3×16)2。=3×22x14+3×16×1.5 所以 yc■4.237mm,7e8,737mm 第二步,通过形心选参考坐标轴y不,求图形对形心轴y乙的损性矩和惯性积。运用平 行移轴公式,得 This document is generated by trial version of Print2Flash(www.print2flash.com)