
省级精品课程一材料力学 第八章弯曲应力 §81纯弯曲时梁横截面上的正应力 上一章我们研究了梁横截面上的内力。为了解决梁的强度问题,必须进一步研究横截面 上内力的分布规律,也就是必须研究横截面上的应力,我们已经知道,在横向力作用下梁横 截面上的内力一般有两个:剪力Q和弯矩M。为了便于研究,同时也考虑到梁的主要变形 是弯曲变形,这里首先研究仅与弯矩M有关的应力 梁的横面上只有弯矩没有剪力的的情况称为纯弯曲。图7-3所示火车车轴的中间一段 的变形就是纯弯曲。练习题7-3()简支梁中间一段的变形也是纯弯曲。我们先研究纯弯曲时 聚横截面上的应力。当然这里假定所研究的梁的变形属于平面弯曲。 在应用截而法时已指出,用平衡方程只能求出横截面上内力的合力。欲解决内力的分布 问题,还必须从研究梁的变形着手。下面依次讨论 、变形的几何关 系变形规律可由实验得到。实验方法是,变形前先在架的侧面上面 横向线aa和bb,并画纵向线11和22,见图8-l(a),然后使梁发生纯弯曲变形,此时可以 观察到如下现象: L- te) 图8-1 横向线仍为直线,但发生相对转动:纵向线部分缩短,另一部分伸长,使一小段直梁变成世 形,根据连续性假定,梁侧面上一定有根纵向线既不缩短也不伸长:横向线与纵向线间的直 角仍不变,见图8-1(b). 为了得到梁内部的变形规律,经过判断和推理,作如下假设:纯弯曲时,梁的横截面仍 保特为平面,并仍然垂直于变形后的梁轴线,但绕藏面内某根轴线转动。这就是所谓平面假 定,根据平面假定所得到的弯曲理论已经得到实验和其他理论的检验。根据平面假定,我们 在梁的表面所观察到的变形规律完全可以推广到梁的内部设想梁是由无数根纵向纤维组 成,则在弯曲变形后,靠近凹入 侧的纤维缩短,靠近凸出一侧的纤维伸长,中间有一层 维既不缩短也不伸长,这就是中性层。中性层与横藏面的交线称为该横截面的中性轴。弯曲 变形时,横截面仍为平面,但绕中性轴转动,见图8-2. 图8-2 3 This document is generated by trial version of Print2Flash(www.printflash.com)

省领精品课程—材料力学 梁的纵向线在弯曲变形后仍垂直于横截面,即直角保持不变,因此纯弯曲时梁的横截面上无 剪应力,只有正应力,见图&3。 ∥ 巡 图8-3 现在可以得到变形的几何关系。如图8-3所示,研究长的微段梁,横截面a和bb在变 形后的夹角为0。令横截面的对称轴为y轴,中性轴为z轴。距中性层为y处的纤维11, 变形后的长度 (pty)d0, 这里P为中性层的曲率半径。而所有纵向纤维的原长度 应等于中性层上纤维的长度,即dx=PdB。因此纵向纤维距中性层为y处11的线应变是 (a) pad 二、物理关系设纵向纤维间无相互挤压,则每一纵向纤维都是单向拉伸或压缩变形。 在比例极限范围内,应用单向拉压时的虎克定律,·=E:,得到 G=B片 (b) 上式说明,任意纵向纤维的拉压应力与它到中性层的距离成正比。在横截面上,任意点处的 正成力与该点到中性轴的距离成正比。即横截面上的正应力沿减面高度按省线规律变化,中 生轴上各点的正应力为零,如图8-3所示。这就是横截面上正应力的分布规律。但在(8-2 式中,p是一个待定的量:中性轴的位置目前尚不知,放测量y的起点未知,因而还不能应 用(8-2)式来计算应力。还必须应用静力平衡条件来解决. 三、静力关系 图8-3画出了横截面上坐标为(y,z)处微面积dA上的微内力。dA。这样的微内力构成 个垂直于横截面的空间平行力系。该力系只可能组成三个内力分量:沿x方向的轴力N, 对z轴的力偶矩2,对y轴的力偶矩My.另一方面,由截面法知,在纯弯曲情况下,N和 y都等于零,z就是横截面上的弯矩M。于是得到 N=odA (c) a This document is gencrated by trial version of Print2Flash (www.print2flash.com)

省领精品课程一材料力学 M =z0dA=0 (d) M,=∫4oA=M (e) 现在讨论以上三式的意义,将(b)式代入(c)式,得 N-fEZu-0 在同一截面处二只有一个值:假定材料的拉压弹性模量相等,则E为常数,故上式可 写成N-台A=0 因为台不可能为,故多续jM=0 (f) 即截面对z轴的面积矩应为零。根据第六章面积矩的性质知,中性轴z必通过横截面的 形心。这就完全确定了中性轴的位置。将(b)代入()式,得 M,=5-∫zdA=0 枚必有2dA=0 (g) 该式表明整个截面对y、z这一对轴的惯性积等于零。由于y轴是对称轴,故知(g)式能自 动满足。将(b)代入()式,得 M,=∫5H=M 所以 台M=台.=M 由此得到 ⊥=M PEL (8-1) 式中1:是截面对中性轴z的惯性矩。(8-1)式决定了梁轴线弯曲变形的曲率。式中EI,称为 梁的抗弯刚度,它代表梁抵抗弯曲变形的能力。现在将(8-1)式代回到)式,即得到纯弯 曲时的正应力公式 (8-2) 135 This document is generated by trial version of Print2Flash(www.printflash.com)

省领精品课程—材料力学 公式(8-1)和(8-2)是在平面假定的基础上得到的。推导过程中又假定梁的纵向纤维 之间无挤压.材料服从虑京定律日比拉压弹性棹最相终。还要说用的是,吊然8-2和8-3 图中均将梁画成矩形截面,但在公式推导过程中并没有使用矩形的几何性质,只要是平面弯 曲问题,上述结论均适用。 现在进一步分析(8-2)式。(8-2)式再次说明横截面的正应力沿截面高度y按直线规 律变化,这里y的测量起点是中性轴,即中性轴上的正应力为零。 以中性轴为界,中性轴的一侧正应力为拉应力,另一侧为压应力。表示拉压应力的正负 号可从(8-2)式中M和y的正负号得到。但根据弯曲变形直接判断更为简使,即以中性轴 为界,梁变形后凸出的一侧受拉,凹入的一侧受压。用这个简便判断法时,公式(8-2)中 的M和y只需用其绝对值即可。 最大正应力发生在离中性轴最远处,即。 M 引用记号 ”大 (8-3) 则有 。0 (8-4) 式中黑称为抗弯截面模量。它是截面的一个几何量。例如,高为h宽为b的矩形截面, ”品沿答 直径为d的圆截面 各种型钢的抗弯截面模量,可在型钢表中查到。 7☑ 图8-4 若梁的横截面对于中性轴不对称,例如图8-4中的T形截面,其最大拉应力和最大压应 136 This document is generated by trial version of Print2Flash(www.print2flash.com)

省领精品课程一材料力学 力不相等,因此它有两个抗弯核面设重。用一土形:大,用来分发计锌员大拉应 力和最大压应力 §8.2横力弯曲时的正应力正应力强度条件 一、横力弯曲时的正应力 工程中的弯曲问题大部分是横力弯曲。与纯弯曲不同,在横力弯曲情况下,染的横截面 上不仅有弯矩M,还有剪力Q。因而横截面上不仅有正应力0,还有剪应力Q。当横减面上 剪应力非均匀分布时,由于各点不同的剪切变形引起横被面翘曲,如图8-5所示。若剪力Q 为常量,各横截面的翘曲相同,因而不影响纵向纤维的伸长或缩短变形,这时仍可应用纯弯 曲时的正应力公式(82)来计算正应力。若剪力Q沿梁的纵向变化时,各横截面的短曲不 由公式〔8-2) 求出的正应力。会有些误差, 但 单性力学 的精确分析告诉我们,对于工 程中常用的跨度1远大于截面高度h的梁,这个误差很小。也即,纯弯曲正应力公式(8-2 式在一般情况下也可用于用横力弯曲情况。不过,横力弯曲时各截面的弯矩不同,故对任意 图8-5 横鞍面,应以M代答(&-2》式中的M,得。=M但y最大的正应力发生在最大弯矩 戴面上离中性轴最远处,即 (8-5) =M W (8-6) 最大弯矩(L)的截面移为危险截面,离中性轴最远的点(y)称为危险点。 二、正应力强度条件及其应用 为了保证梁不破坏,必须使梁的最大正应力(工作应力)不超过材料的抗弯容许应力 137 This document is generated by trial version of Print2Flash(www.printflash.com)
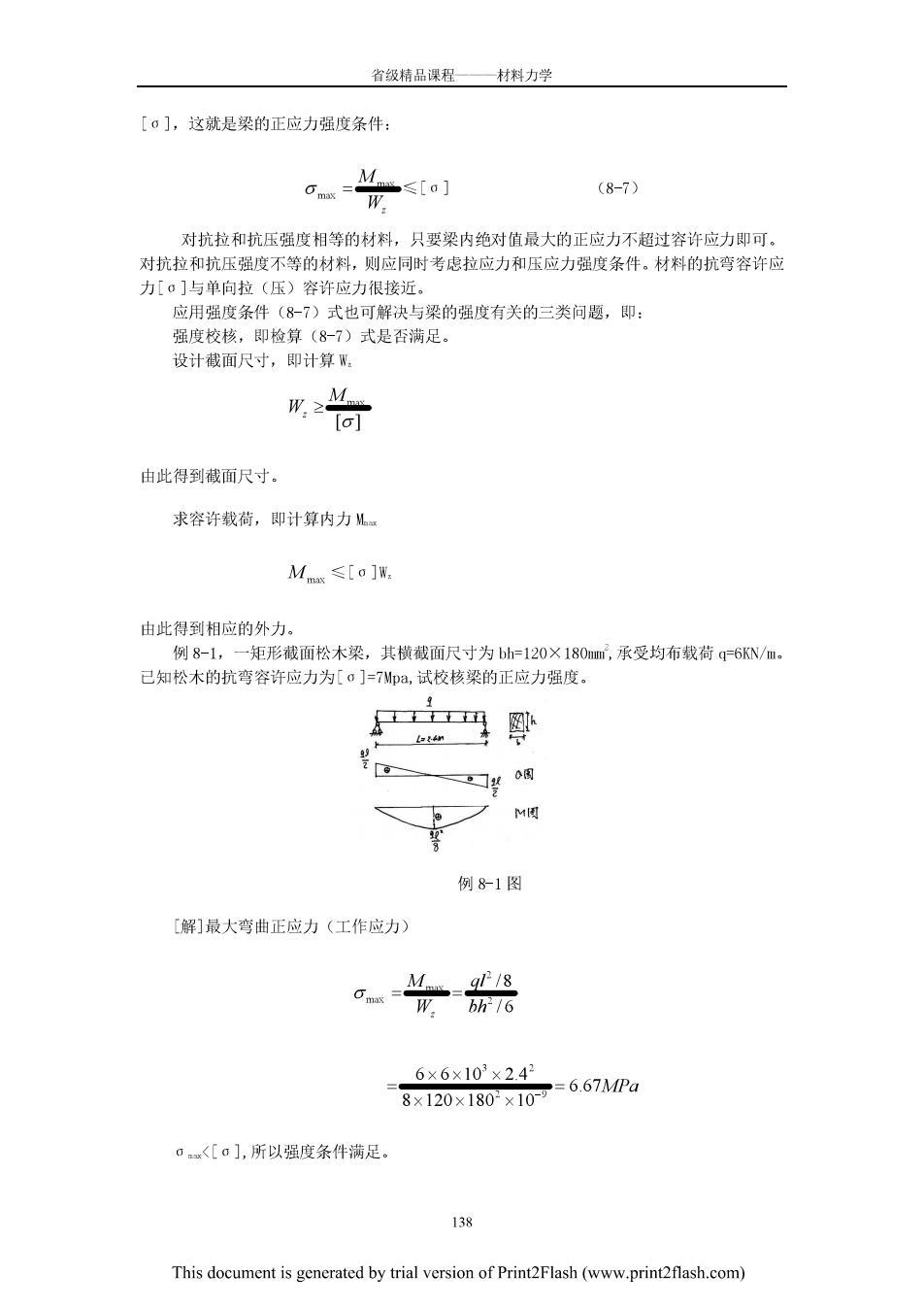
省级精品课程—材料力学 【。],这就是梁的正应力强度条件: (8-7) 对抗拉和抗压强度相等的材料,只要梁内绝对值最大的正应力不超过容许应力即可 对抗拉和抗压强度不等的材料,则应同时考虑拉应力和压应力强度条件。材料的抗弯容许应 力[·]与单向拉(压)容许应力很接近。 应用强度条件(87)式也可解决与梁的强度有关的三类问题,即: 强度校核,即检算(87)式是否满足。 设计截面尺寸,即计算 简 由此得到截面尺寸。 求容许载荷,即计算内力儿 Mm≤[o]W 由此得到相应的外力 例8-1,一矩形被面松木梁,其横藏面尺寸为bh-120×180m,承受均布载荷q6N/m, 已知松木的抗弯容许应力为[a]=7Mpa,试校核梁的正应力强度. M因 例81图 解]最大弯曲正应力(工作应力 6×6×103×2.4 8x120x180-x10=6.67MPa ·<[0],所以强度条件满足。 This document is generated by trial version of Print2Flash(www.print2flash.com)
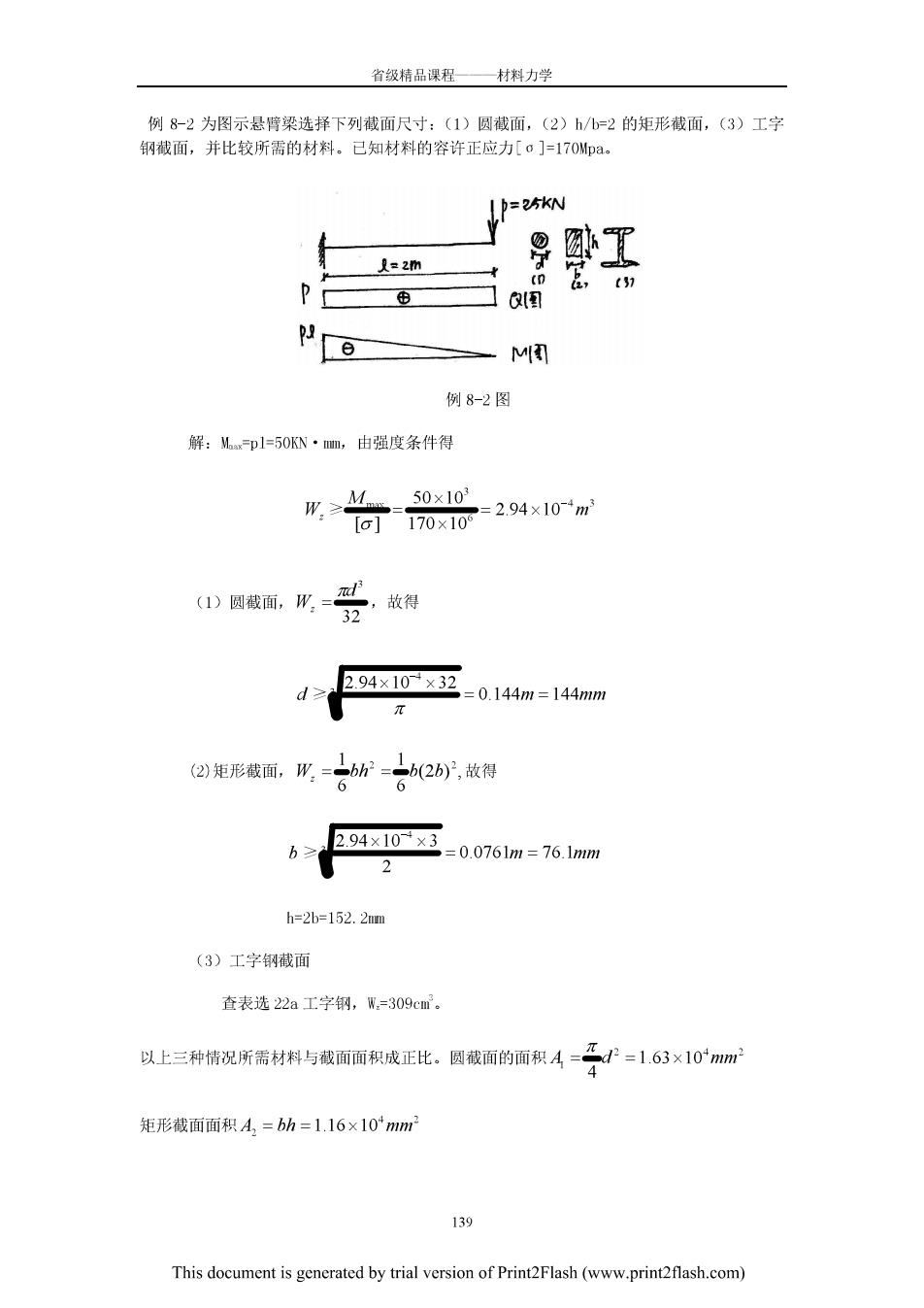
省领精品课程 一材料力学 例8-2为图示悬臂染选择下列藏面尺寸:(1)圆被面,(2)h/b=2的矩形截面,(3)工字 钢截面,并比较所需的材料.已知材料的容许正应力[o]=170Mpa. T 1=2m P 0图 T 例8-2图 解:cpl=50KN·m,由强度条件得 可770x10=294×10m 50×10° 医碳属,化 ,故得 d 294x10x32=0.144m=144mm (②)矩形截面,W=。bhb(2b,故得 b 294x10x3=0.0761m=76.1mm 2 h=2b=152.2m (3)工字钢截面 查表选22a工字钢,黑=309cm。 以上三种情况所需材料与截面面积成正比。圆截面的面积A=二=1.63×10mm 矩形截面面积A,=bh=116×10mm 139 This document is generated by trial version of Print2Flash(www.printflash.com)

省级精品课程—材料力学 查表得工字钢截面积A,=0.42×10mm 其比值为A:A:A=1:0.712:0.258 由此可见,从满足弯曲正应力强度条件来看,工字钢截面最省料,矩形截面次之,圆 截面最差 §8.3弯曲剪应力 梁在横力弯曲时,其横截面上除了弯矩外,还有剪力,相应地就有剪应力。本节将分析 几种被面形状梁的剪应力,与前面的正应力分析一样,仍限于研究外力作用在梁的纵向对称 面的情况。 ·、矩形截哉面级 设矩形藏面的高为h宽为b,截面上的剪力Q沿截面的纵对称轴y作用。(图8-6b)注 意到梁的侧面是自由表面,由剪应力互等定理知,横面侧边上各点的剪应力方向都平行于 侧边。对于狭长的矩形截面来说,可以认为剪应力的大小和方向沿截面宽度的变化不大。因 此,可以对矩形截裁面剪应力的分布规律作如下假定: (1)横截面上各点剪应力的方向都平行于侧边,也即平行于剪力Q: (2)沿战面的☆度道应力均匀分布 进一步研究表明, 以上述假定为基础的解与精确解相比有足够的准确度, 现在研究剪应力的大小沿高度的变化规律。 ws证 图8-6 用截面1-1和2-2取出一长为x的微段梁,为简单起见,设微段梁两截面上的剪力Q相等 而弯矩却不同,见图8-6(a)和(c)。弹性理论的分析表明,对于剪力Q沿梁长变化的情况, 用这个简化方法得到的结果也是足够精确的。与剪力和弯矩对应地在两面上有正应力 剪应力t,见图8-6(d)。但用这一段柴仍无法说明剪应力t沿高度的分布问题,为此,在 距中性轴为y处,用平行于中性层的平面3-3将做段梁切开,取下部一小块来分析:小块的 左右侧面上有正应力和剪应力x,根据剪应力互等定理,它等于横藏面上距中性轴为y处的 140 This document is gencrated by trial version of Print2Flash(www.print2flash.com)

省领精品课程一材料力学 剪应力,见图86()和()。研究小块在x方向的平衡条件,计算小块侧面和顶面上内力 的合力 N-ja=1兰4兰 a=a T=7'bdx=t bdx 由平衡条件ΣX=0,即NN-T=0 ÷0 红起0兴:究 (8-8) 这就是矩形截面矩中性轴为y处的剪应力公式。要特别注意式中S是距中性轴为y的横线以 外的部分横截面面积A对中性轴的面积矩,它是一个变量,随着距离y而改变。如图8-7 新示 图8-7 修冷归共 o h 以: -74-y) 14 This document is generated by trial version of Print2Flash(www.printflash.com)

省领精品课程—材料力学 由此可见。剪应力的大小沿矩形鞍面的高度二次抛物线规律变化。在上下边峰y=士分》处 =0:在中性轴上(y=0)剪应力达到最大值: 受 代A1,管得 品兴 (8-9) 即矩形截面的最大剪应力是平均剪应力的3/2倍。 二、工字型截面梁及其他组合矩形藏面梁 图8-8 工字型截面由腹板和冀缘两部分组成(图&-8)。由于腹板是狭长矩形,故仍可用公式 (8-8)来计算剪应力。 此时b为腹板的宽度,S为图中8-8中阴影线部分的面积对中性轴的面积矩 S=B号号+分+空-停+分 是H-)+-4) 于是 tW-)+-4 This document is gencrated by trial version of Print2Flash (www.print2flash.com)