新疆大学：《工程力学》课程教学资源（习题指导）第7章 弹性杆件横截面上的正应力分析

第7章弹性杆件横截面上的正应力分析 面的正受力际示，其上所有杆模截面均为20mmX0m的矩形，试杆CEDE 解：图(a)中，c0s- (1) 截面法受力图(a) ΣM=0,Fa×4-05+5)×3=0(2) E150Es0=40 (3) (1)代入(3.得FaE=50kN 15x103 号-02k0as-15MP aDE-FoE-50 MPa 习题7从图 7一2图示直杆在上半部两侧面受有平行于杆轴线的均匀分布载荷，其集度方=1OkNm,在白由端D 处作用有集中呼斤=20kN。已知杆的横截面面积A=20×10m,=4m。试求： 的大并指明其作用位置 F(N 解：由已知，用截面法求得 Do-子·81e-20Mr 40×103 -100 MPa E-5￥=150Ma (l y (2)m=4=200MP(截面) 习题72图 7一3图示铜芯与铝壳组成的复合材料杆，轴向拉伸找荷F通过两端的刚性板加在杆上。试： E4.=Ed (1) Fy +F =Fi (2) K“A+4 E Fp 母+60- E,F。 g+g,0-的 习73图 4 4×105x10°×171×103 2.,"105X10xax02s+20×10Xx006-0025-835MPma ,ag-35x0-56M 7-4 -58

— 58 — 习题 7-1 图 15kN 15kN 5kN  5kN  FDE C D 4m 3m FCE (a) 习题 7-2 图 C B D A E 30 20 40 (kN) FNx (a) 习题 7-3 图 第 7 章 弹性杆件横截面上的正应力分析 7－1 桁架结构受力如图示，其上所有杆的横截面均为 20mm×50mm 的矩形。试求杆 CE 和杆 DE 横 截面上的正应力。 解：图（a）中， 5 4 cos = （1） 截面法受力图（a）  MD = 0 ， FCE 4 − (15+ 5)3 = 0 （2） FCE = 15 kN  Fx = 0 ， FDE cos = 40 （3） （1）代入（3），得 FDE = 50 kN ∴ 15 0.02 0.05 15 103 =   = = A FCE  CE MPa = = 50 A FDE  DE MPa 7－2 图示直杆在上半部两侧面受有平行于杆轴线的均匀分布载荷，其集度 p = 10kN/m，在自由端 D 处作用有集中呼 FP = 20 kN。已知杆的横截面面积 A = 2.0×10-4m 2，l = 4m。试求： 1．A、B、E 截面上的正应力； 2．杆内横截面上的最大正应力，并指明其作用位置。 解：由已知，用截面法求得 FNA = 40 kN FNB = 20 kN FNE = 30 kN （1） 200 2.0 10 40 10 4 3 N =   = = − A F A  A MPa 100 N = = A F B  B MPa 150 N = = A F E  E MPa （2）  max = A = 200 MPa（A 截面） 7－3 图示铜芯与铝壳组成的复合材料杆，轴向拉伸载荷 FP通过两端的刚性板加在杆上。试： 1．写出杆横截面上的正应力与 FP、d、D、Ec、Ea 的关系式； 2．若已知 d = 25mm，D = 60mm；铜和铝的单性模量分别为 Ec = 105GPa 和 Ea = 70GPa，FP = 171 kN。 试求铜芯与铝壳横截面上的正应力。 解：1．变形谐调： a a Na c c Nc E A F E A F = （1） FNc + FNa = FP （2） P c c a a c c Nc F E A E A E A F + = P c c a a a a Na F E A E A E A F + = ∴          − + = =  +  − = + = = 4 π( ) 4 π ( ) 4 π 4 π 2 2 a 2 c a P a Na a 2 2 a 2 c P c c a a c P c Nc c D d E d E E F A F E D d d E E F E A E A E F A F c   2． 83.5 105 10 π 0.025 70 10 π (0.06 0.025) 4 105 10 171 10 9 2 9 2 2 9 3 c =    +    −      = MPa 55.6 105 70 83.5 c a a = c =  = E E   MPa 7－4 图示由铝板钢板组成的复合材料柱，纵向截荷 FP通过刚性平板沿着柱的中心线施加在其上。试： 1．导出复合材料柱横截面上正应力与 FP、b0、b1、h 和 Ea、Es之间的关系式；

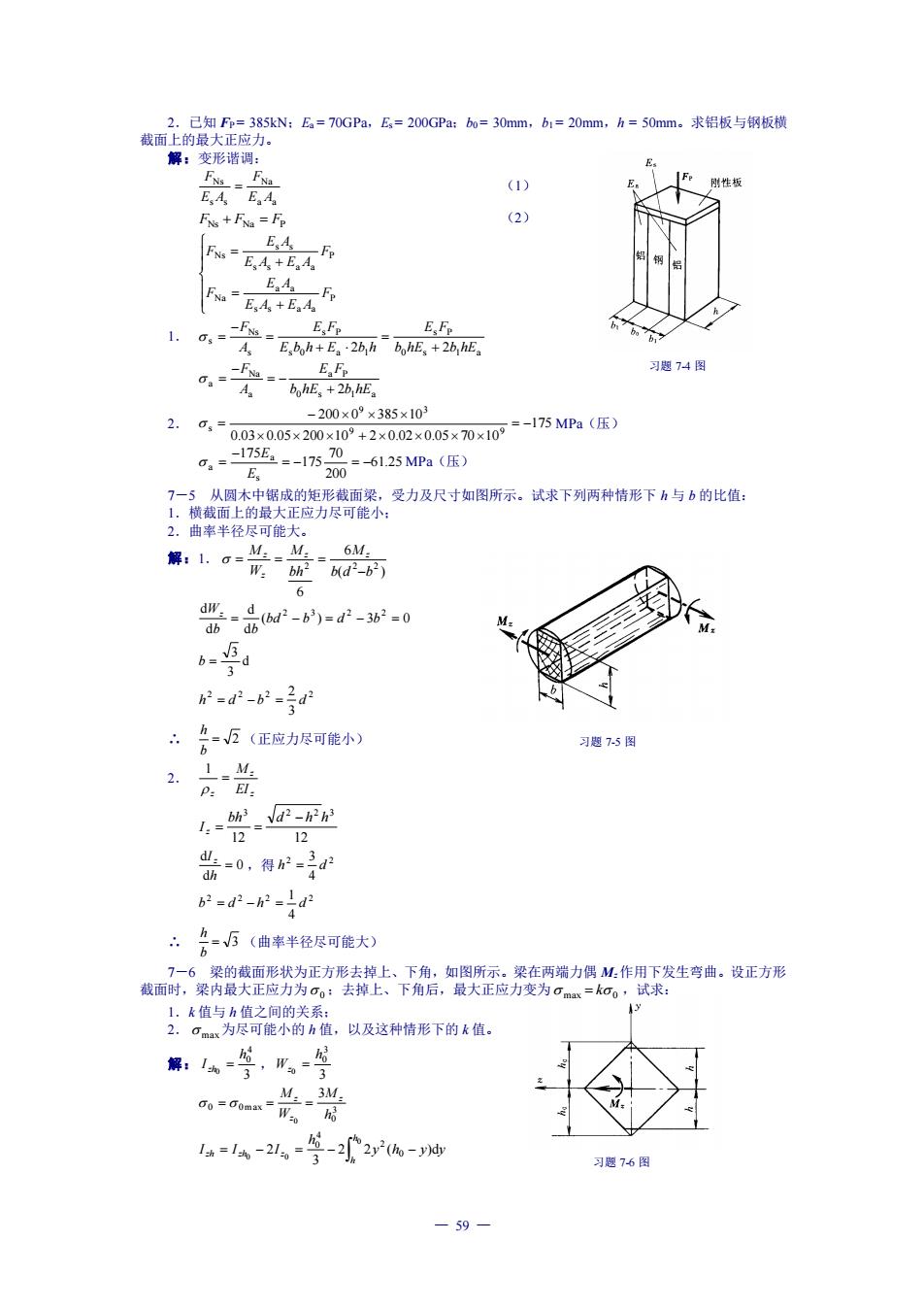
拔面子的任资N:=0Ga,&=20GP=30am,=20mh=50am,求铝板与锅版候 解：变形谐调： FNs +FN=F (2) 习题74图 300×09385×103 2.6-03x05x2090*2020050x10-75M(压) G,=-175=-17570=61.25MPa(压) 2.曲率半径尽可能大 解：1.=是=0 恶-6-0 三三 =2-62- “=反（正应力尽可能小） 习75图 2面 1M. 兽=0，得- 62=d2-2=d ·么=5（曲米半径尽可能大） 解：答，用号 0兴 4=1-2-空-2%- 习题76国 -59

— 59 — 习题 7-4 图 习题 7-5 图 习题 7-6 图 2．已知 FP = 385kN；Ea = 70GPa，Es = 200GPa；b0 = 30mm，b1 = 20mm，h = 50mm。求铝板与钢板横 截面上的最大正应力。 解：变形谐调： a a Na s s Ns E A F E A F = （1） FNs + FNa = FP （2）        + = + = P s s a a a a Na P s s a a s s Ns F E A E A E A F F E A E A E A F 1． 0 s 1 a s P s 0 a 1 s P s Ns s 2 b hE 2b hE E F E b h E b h E F A F + = +  = −  = 0 s 1 a a P a Na a b hE 2b hE E F A F + = − −  = 2． 175 0.03 0.05 200 10 2 0.02 0.05 70 10 200 0 385 10 9 9 9 3 s = −    +     −     = MPa（压） 61.25 200 70 175 175 s a a = − = − − = E E  MPa（压） 7－5 从圆木中锯成的矩形截面梁，受力及尺寸如图所示。试求下列两种情形下 h 与 b 的比值： 1．横截面上的最大正应力尽可能小； 2．曲率半径尽可能大。 解：1． ( ) 6 6 2 2 2 b d b M bh M W M z z z z −  = = = ( ) 3 0 d d d d 2 3 2 2 = bd − b = d − b = b b Wz d 3 3 b = 2 2 2 2 3 2 h = d − b = d ∴ = 2 b h （正应力尽可能小） 2． z z z EI M =  1 12 12 3 2 2 3 bh d h h I z − = = 0 d d = h I z ，得 2 2 4 3 h = d 2 2 2 2 4 1 b = d − h = d ∴ = 3 b h （曲率半径尽可能大） 7－6 梁的截面形状为正方形去掉上、下角，如图所示。梁在两端力偶 Mz作用下发生弯曲。设正方形 截面时，梁内最大正应力为  0 ；去掉上、下角后，最大正应力变为  max  0 = k ，试求： 1．k 值与 h 值之间的关系； 2． max 为尽可能小的 h 值，以及这种情形下的 k 值。 解： 3 4 0 0 h I zh = ， 3 3 0 0 h Wz = 3 0 0 0max 3 0 h M W M z z z  =  = = y h y y h I I I h h zh zh z 2 2 ( )d 3 2 0 2 4 0 0 0 0 = − = − − 

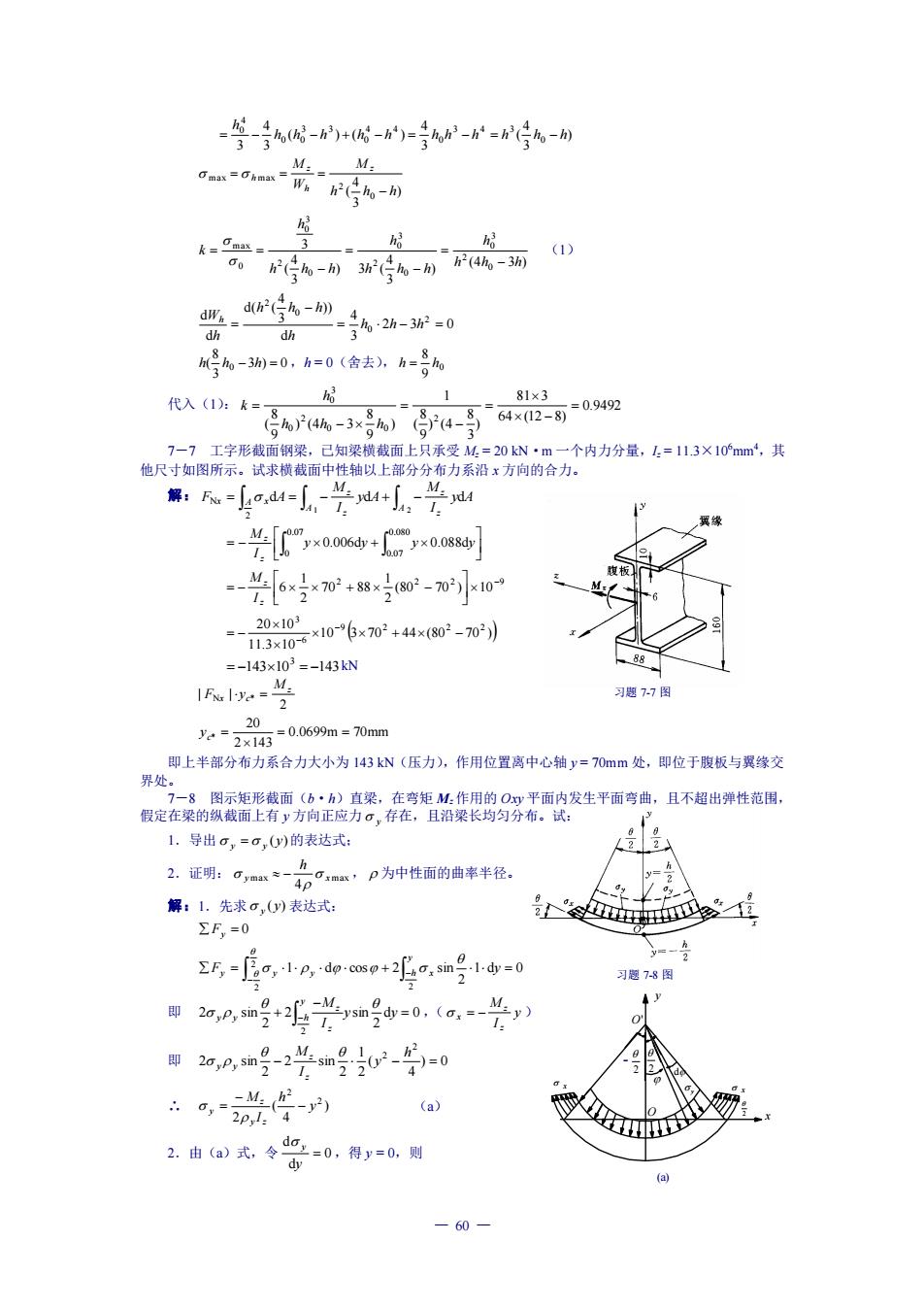
一答-含优-的+代-的-音2-n写A-创 0-0-w M: 3 。写%-3-动A-功④ k-可ma= 00-0 d h-3动)=0，A=0(舍去).h=o 入-3含4-高4：方ag =20kN -4[”x006+Cyx0o购 -[6+-小0 -8062-） =-143×103=-143kw 习7-7图 20 食定在菜的飘获智套雷方尚亮装，存在距新限的9面内发生平面弯自、且不超出养性范围， 1.导出，=,0)的表达式 2.证明：，mx一x,p为中性面的曲率半径 人 解：1先求0，表达式 Σ万，=信a,lp,dp:csp+2o,smgl=0 习题78 甲%号号兰m0,0兰 即2，m号-2兰m号02-=0 2由a式令号=0，得y=0则 -60

— 60 — 习题 7-7 图 习题 7-8 图 O' y 2−  d 2 O 2 x  x  x  y (a) ) 3 4 ( 3 4 ( ) ( ) 3 4 3 0 3 4 3 0 4 4 0 3 3 0 0 4 0 h h h h h h h h h h h h = − − + − = − = − ) 3 4 ( 0 2 max max h h h M W M z h z h −  =  = = (4 3 ) ) 3 4 ) 3 ( 3 4 ( 3 0 2 3 0 0 2 3 0 0 2 3 0 0 max h h h h h h h h h h h h k − = − = − = =   （1） 2 3 0 3 4 d )) 3 4 d( ( d d 2 0 0 2 =  − = − = h h h h h h h h Wh 3 ) 0 3 8 ( h h0 − h = ，h = 0（舍去）， 0 9 8 h = h 代入（1）： 0.9492 64 (12 8) 81 3 ) 3 8 ) (4 9 8 ( 1 ) 9 8 ) (4 3 9 8 ( 2 0 0 2 0 3 0 =  −  = − = −  = h h h h k 7－7 工字形截面钢梁，已知梁横截面上只承受 Mz = 20 kN·m 一个内力分量，Iz = 11.3×106mm4，其 他尺寸如图所示。试求横截面中性轴以上部分分布力系沿 x 方向的合力。 解：    = = − + − 1 2 2 N d d d A z z A z z x A x y A I M y A I M F  A       = −  +    y y y y I M z z 0.006d 0.088d 0.080 0.07 0.07 0 2 2 2 9 (80 70 ) 10 2 1 70 88 2 1 6 −       = −   +  − z z I M 10 (3 70 44 (80 70 )) 11.3 10 20 10 9 2 2 2 6 3   +  −   = − − − 143 10 143 3 = −  = − kN 2 | | N * z x c M F y = 0.0699m 70mm 2 143 20 * = =  yc = 即上半部分布力系合力大小为 143 kN（压力），作用位置离中心轴 y = 70mm 处，即位于腹板与翼缘交 界处。 7－8 图示矩形截面（b·h）直梁，在弯矩 Mz作用的 Oxy 平面内发生平面弯曲，且不超出弹性范围， 假定在梁的纵截面上有 y 方向正应力  y 存在，且沿梁长均匀分布。试： 1．导出 (y)  y = y 的表达式； 2．证明： max max 4 y x h     − ，  为中性面的曲率半径。 解：1．先求 (y)  y 表达式：  Fy = 0  − −  =     +   = y y y y h x F y 2 2 2 1 d 0 2 1 d cos 2 sin         即 d 0 2 2 sin 2 2 sin 2 = − + − y y I y M h z z y y     ，（ y I M z z  x = − ） 即 ) 0 4 ( 2 1 2 2 sin 2 2 sin 2 2 −  − = h y I M z z y y     ∴ ) 4 ( 2 2 2 y h I M y z z y − − =   （a） 2．由（a）式，令 0 d d = y  y ，得 y = 0，则 - 2  2 

-h24. h M. 1一》图不好管和铝管牢图地粘成复合材料管，在两装力保从作用下发生平面弯鱼。试。 2.已知D=2 d. 和铝管横酸面上的眼大正皮力。 :D=4m:=00Nm:=210GPa,=70GPa.求钢管和铝 解：静力平衡： 立品 (3) 由a)从歌以 (4) 代入得0欲业= 习题79图 (5) 上兰2兴“w-号号 64E.M. 64E.My (Bsys) 36*x10=54.1MP 解：根据平面假设，应变沿截面高度作直线变化 。沿截面高度直线的斜率不同“中性轴不过截面形心。 50 【,确定中性轴位置。设拉压区高度分别为、k 由工=0,得：-hb+n么b=0 习题710图 即 (1) (2 :友=反-h=414m(中性轴的位置) ∴=(2-5h=58.6mm 2.M.-yod+yod-cu+E-cu+y.2E.cd -61

— 61 — 习题 7-9 图 习题 7-10 图 Ch t   t  C  C (a) ht max 2 ,max 4 4 2 8 4 x z z z y z y z y z y h W h M h I h M I h M       −   −  = − = − = （b） 7－9 图示钢管和铝管牢固地粘成复合材料管，在两端力偶 Mz作用下发生平面弯曲，试： 1．导出管横截面上正应力与 Mz、D1、D2、D3和钢的 Es、铝的 Ea 之间的关系式； 2．已知 D1 = 20mm，D2 = 36mm，D3 = 44mm；Mz = 800N·m；Es = 210GPa，Ea = 70GPa。求钢管和铝 和铝管横截面上的最大正应力  max。 解：静力平衡： Ma + Ms = Mz （1） 变形谐调：  a = s 得 s s s a a a E I M E I M = （2） 64 π( ) 4 2 4 3 a D D I − = ， 64 π( ) 4 1 4 2 s D D I − = （3） 由（2） s s s a a a M E I E I M = （4） 代入（1），得 M M z E I E I + s = s s a a (1 ) s s a a s s s E I E I E I M M z + = （5） ∴ M z E I E I E I M s s a a a a a + = （6） 1． π [ ( ) ( )] 64 4 2 4 a 3 4 1 4 s 2 s s s a a s s s s E D D E D D E M y y E I E I E M y I M z z − + − = − + = − −  = ，（ 2 2 1 D2 y D   ） π [ ( ) ( )] 64 4 2 4 a 3 4 1 4 s 2 a s s a a a a a a E D D E D D E M y y E I E I E M y I M z z − + − = − + = − −  = ，（ 2 2 2 D3 y D   ） 2． 133 π[210 (36 20 ) 70 (44 36 )] 10 64 210 800 18 10 4 4 4 4 12 3 smax =  − +  −      = − −  MPa 54.1 π[210 (36 20 ) 70 (44 36 )] 10 64 70 800 22 10 4 4 4 4 12 3 a max =  − +  −      = − −  MPa 7－10 由塑料制成的直梁，在横截面上只有 Mz作用，如图所示。已知塑料受拉和受压时的弹性模量 分别为 Et和 Ec，且已知 Ec = 2Et；Mz = 600N·m。试求： 1．梁内最大拉、压正应力； 2．中性轴的位置。 解：根据平面假设，应变沿截面高度作直线变化 ∵ Ec = 2Et， = E ∴  沿截面高度直线的斜率不同 ∴中性轴不过截面形心。 1．确定中性轴位置。设拉压区高度分别为 ht、hc 由  Fx = 0 ，得： 0 2 1 2 1 −  c max hc b +  t max  ht b = 即 c c c t t max cmax h h h h h − = =   （1） 又∵ t c t max cmax t t max c cmax t max cmax 2 2 h h E E = = =       （2） 由（1）、（2），得 c c t c c c 2 2 h h h h h h h h − = = − 即 2 c 2 (h − hc ) = 2h      = − =  = − = (2 2) 58.6mm ( 2 1) 41.4mm t c h h h h （中性轴的位置） 2．       = + = + = +  t c t c t c td cd t td c cd t td 2 t cd A A A A A A M z y A y A yE  A yE  A yE  A y E  A

-4+24-4+24-g4+2) 其中1，+2，-答2x婴-的6-4 + 2x600×414x10 =8.69MPa(压) =6.15MPa(拉) 磊，。素组各中所示的二杆横载面上最大正应力的比位。 (6)为单向拉伸 出丑 习题1.11图 7一12桥墩受力如图所示，试确定下列找荷作用下图示截面BC上A小、B两点的正应力： .仅在点1或点3处承受40kN的压缩载荷。 5 40×10 =40MPa -=-8MPa 2.=2-2x40x0.010x1 -I5.3MPa 习712图 75×200 3.在点1加载： 5x200 4=733MPa, d8 -2.67MP 发面管，首壁厚=5m,管在两端承受轴向我荷小、已知开孔 F处的正 2.177x10m,F=25kN.试球 -62

— 62 — 习题 7-11 图 习题 7-12 图 d 2 d d 2 d ( 2 ) t c t t t c t t c t c I I E A y A y y E y A y A E y A A A A  = +      =  +        = +          其中 (6 4 2) 3 3 2 3 2 3 3 c 3 t t + c = +  = − bh bh bh I I ∴ ( 2 ) 1 t t c E I I M z + =  ∴ c t c c t t c c c c cmax 2 2 2 h I I M h I I M E E h E z z + = + = =   8.69 (6 4 2) 10 3 50 100 2 600 41.4 10 12 3 3 = −      = − − MPa（压） ∴ 6.15 10 (6 4 2) 3 50 100 600 (2 2) 100 10 2 12 3 3 t t c t t t max =  −   −   = + = = − − h I I M h E z   MPa（拉） 7－11 试求图 a、b 中所示的二杆横截面上最大正应力的比值。 解：（a）为拉弯组合 2 P 2 P P a 3 4 6 ) 2 3 ( 4 2 3 a F a a a F a a F =   +   = （b）为单向拉伸 2 P b a F  = ∴ 3 4 b a =   7－12 桥墩受力如图所示，试确定下列载荷作用下图示截面 ABC 上 A、B 两点的正应力： 1．在点 1、2、3 处均有 40 kN 的压缩载荷； 2．仅在 1、2 两点处各承受 40 kN 的压缩载荷； 3．仅在点 1 或点 3 处承受 40 kN 的压缩载荷。 解： 2.67 200 75 10 40 10 6 3 N =    = − A F x Mpa 40 10 6 75 100 40 10 0.125 9 2 3 =     = W − M z MPa 1． 8 200 75 3 3 40 103 N = −    = = − = A F x  A  B MPa 2． 15.3 6 75 200 2 125 80 10 200 75 2 2 40 10 2 3 3 N = −    −  −   = − − = W M A F x z  A MPa 3．在点 1 加载： 12.67 6 75 200 40 10 125 200 75 40 10 2 3 3 N = −    −  −  − = − = W M A F x z  A MPa 7.33 6 75 200 40 10 125 200 75 40 10 2 3 3 N =    +  −  + = − = W M A F x z  B MPa 由对称性，得 在 3 点加载：  A = 7.33 MPa， B = −12.67 MPa 7－13 图示侧面开有空洞的正方形截面管，管壁厚  = 5mm，管在两端承受轴向载荷 FP。已知开孔 处截面的形心为 C，形心主惯性矩 6 0.177 10− I z =  m 4，Fp = 25kN。试求： 1．开孔处横截面上点 F 处的正应力；

席，大正应力。 ==25kN M.=E×(25-18.57×103=160.75N·m A■(50×5×2+40×5)×106=700×106m2 2.= =6426MPa(在y正向最大位置) 2.在上述方值下点A的正应力值。 今兰会会 6 2兴 1.◆0-0,6m-2n-0 避7 由 (2) ,0102x75-3x25=40M 757 为圆富：以中所示为承受氨向载衡的人骨受力筒图，假定实心合器 1·确定截而B一B上的应力分布： 力。动是份中为经为清整外径的一半)由离棉状骨质所组成且怎略海绵状承受位力的能 3.确定1、2两种情况下，骨骼在截面B一B上最大压应力之比。 -63

— 63 — 习题 7-13 图 习题 7-14 图 习题 7-15 图 A B z O y (a) 0.795 14.526 y (b) y A B +14.43MPa 16.55MPa O C C z z (d) y O A C B O 12.6mm 14.1mm z +13.73MPa −15.32MPa C z (c) O B 2．最大正应力。 解： FNx = FP = 25 kN (25 18.57) 10 160.75 3 = p  −  = − Mz F N·m 6 6 (50 5 2 40 5) 10 700 10 − − A =   +   =  m 2 1． 18.57 10 18.85 N 3 = =   = − z x z F I M A F  MPa 2． A FNx  max = 3 (50 18.57) 10− =  −  z z I M = 64.26 MPa（在 y 正向最大位置） 7－14 图示矩形截面杆在自由端承受位于纵向对称面内的纵向载荷 FP，已知 FP = 60kN。试求： 1．横截面上点 A 的正应力取最小值时的截面高度 h； 2．在上述 h 值下点 A 的正应力值。 解： 6 40 ) 2 ( 40 2 P N P h d h F h F W M A F z x z A −  = + = + ) 2 3 ( 20 2 P h F h − d = （1） 1．令 = 0   h  A ， 0 6 2 4 2 = − h hd h ∴ h = 3d = 75mm （2） 2．由（1）、（2）式得： ) 40 75 2 75 3 25 ( 20 60 10 2 3 =   −   A = MPa 7－15 图中所示为承受纵向载荷的人骨受力简图，假定实心骨骼 为圆截面。试： 1．确定截面 B－B 上的应力分布； 2．假定骨骼中心部分（其直径为骨骼外径的一半）由海绵状骨质所组成，且忽略海绵状承受应力的能 力，确定截面 B－B 上的应力分布； 3．确定 1、2 两种情况下，骨骼在截面 B－B 上最大压应力之比。 解：1． 0.795 4 π 26.7 445 10 2 6 1 N N1 = −   = − = A F x  MPa 14.526 10 32 π 26.7 445 61 10 9 3 3 1 M max =     = = − − z z W M  MPa

∴.at.=14.526-0.795=13.73MPa =-14526-0795-1532MPg 沿y方向应力分布如图（心）所示，中性轴为： 2 445x106 4x445105 x(26,72-26 =-0,795x=-1.06MPa x×26.70- M. 14526x6=15.494MP 0x=15.494-1.06=l4.43Mpam =-15.494-1.06=-16,55MPa c为中性轴，沿y轴应力分布如图(d) 3.g-6-108,成g-1-0926 解，4=5×10×106=50x×105m 形5x102 1010m =10x5 M,=1000×5x10-3=5N·m M.=1000x25x103=25N·m 习题7-16图 1000525x10=140MPa 50+ 6,(A)=-300x106,G,(B)=-900x106,G,(D)=-100×10。若己知锅的弹性模量E=200GPa。试求： 解：A=1001 0 -01x10=1010 =100x60 6 -x10-4=60x10-6m =- M:=Fy M,=-Fpy (2) o"(6品+品+需x10 3) a-Ee (4) -64

— 64 — 习题 7-16 图 A z y M y C M z 10 5 (a) 习题 7-17 图 ∴ max =14.526 − 0.795 =13.73 +  MPa max = −14.526 − 0.795 = −15.32 −  MPa 沿 y 方向应力分布如图（c）所示，中性轴为 zc。 2． 4 ) 2 26.7 π(26.7 ( 445 10 2 2 6 2 2 −  = = − A FNx  N ) 4 1 π 26.7 (1 4 445 10 2 6  − −   = 1.06 3 4 = −0.795 = − MPa 15.494 15 16 14.526 ) ) 2 1 (1 ( 4 1 2 2max =  = − = = z z z z M W M W M  MPa max =15.494 −1.06 =14.43 +  Mpan max = −15.494 −1.06 = −16.55 −  MPa zC为中性轴，沿 y 轴应力分布如图（d） 3． 1.08 15.32 16.55 1 2 = = − −   ，或 0.926 16.55 15.32 2 1 = = − −   7－16 正方形截面杆一端固定，另一端自由，中间部分开有切槽。杆自由端受有平行于杆轴线的纵向 力 FP。若已知 FP =1kN，杆各部分尺寸示于图中。试求杆内横截面上的最大正应力，并指出其作用位置。 解： 6 6 5 10 10 50 10 − − A=   =  m 2 9 6 2 10 12 1 10 6 5 10 − − −  =   Wy = m 3 9 6 2 10 24 1 10 6 10 5 − −  =   Wz = m 3 FNx = 1 kN 1000 5 10 5 3 =   = − M y N·m 1000 2.5 10 2.5 3 =   = − M z N·m z z y x y W M W M A F = + + N  max 10 140 24 1 2.5 12 1 5 50 1000 6  =             = + + MPa 最大正应力作用位置位于中间开有切槽的横截面的左上角点 A，如图（a）所示。 7 －17 钢制 立柱 上 承受 纵向 载荷 FP 如图 所示 。 现在 A、B、D 三处 测得 x 方向 的正 应 变 6 ( ) 300 10−  x A = −  ， 6 ( ) 900 10−  x B = −  ， 6 ( ) 100 10−  x D = −  。若已知钢的弹性模量 E = 200GPa。试求： 1．力 FP的大小； 2．加力点在 Oyz 坐标中的坐标值。 解： 6 3 100 60 10 6 10 − − A =   =  m 2 9 6 2 10 100 10 6 60 100 − −  =   Wz = m 3 9 6 2 10 60 10 6 100 60 − − −  =   Wy = m 3 FNx = −FP M F y z =  P M F y y = − P N P P P 6 ) 10 6000 100 60 (  − − + − = − + = F F y F z W M W M A F y y z x z  A （1） P P P 6 ) 10 6000 100 60 (  − + + − = F F y F z  B （2） P P P 6 ) 10 6000 100 60 ( + +  − = F F y F z  D （3）  = E （4）

由0.4.（品-动0-2010x4-3010) 即（总斋=0 (5) 由2.④（品+流-需=-0 (6) 由(3(4(d+品+0r=-20 (7) 4 解(5、(6)、(7)：p=0.02m=20mm e=-0.025m=-25mm 7一18形截而柱受力0 习是7H3图 保组合变形下的正应力（图。 a= Fp(Fp.p)=(Feyp).y A 2 12 (1) 将-名，代入(1)式，并使正应力为零，得 厅所作用的直线方程 整理得，号+普= 的中居蓝程商定，◆等于得后 1+是：+y=0 12 (2) 一丹 中性轴n一n的截距： (3) 明中性 区域是拉应力区（见图b) 作用下的区城为，的 如果将(2)改写为是+=- (4) 12 12 点化锁上二到明定，即中性轴可绕该 由(4)式，F作用必沿直线移动。由(3)式，2 一2直线的截距值大于1一1直线的。所以，当中性轴1 -65

— 65 — n n y z C ot y ot z FP (b) 习题 7-18 图 A D C B y h P F z K ( . ) P P y z ( y.z) F b (a) C z 2 1 1 2 z FP2 FP1 (c) 由（1）、（4）， ) 10 200 10 ( 300 10 ) 6000 100 60 1 ( 9 6 P P P 6 − − −   =   −  − F y z 即 ) 60 6000 100 60 1 ( P P P − − = − − F y z （5） 由（2）、（4）， ) 180 6000 100 60 1 ( P P + − = − − F y z （6） 由（3）、（4）， ) 20 6000 100 60 1 ( P P P + + = − − F y z （7） 解（5）、（6）、（7）： zP = 0.02m = 20 mm yP = −0.025m = −25mm FP = 240 kN 7－18 矩形截面柱受力如图所示，试证明： 1．当铅垂力 FP作用在下面方程所描述的直线上的 任意点时，点 A 的正应力等于零： 1 6 6 P P + = h y b z 2．为了使横截面的所有点上都不产生拉应力，其作 用点必须位于由类似上述方程所描述的直线围成的区域 内（图中虚直线围成的区域）。 解：1．写出 K 点压弯组合变形下的正应力（图 a）。 12 ( ) 12 ( ) 3 P P 3 P P P bh F y y hb F z z A F  −    = − −             = − + + y h y z b z hb F 12 12 1 2 P 2 P P （1） 将 ) 2 , 2 ( h b A − − 代入（1）式，并使正应力为零，得 FP所作用的直线方程 0 6 6 1 P P − − = h y b z 整理得： 1 6 6 P P + = h y b z 2．若 FP 作用点确定，令（1）式等于零，得截面 的中性轴方程（图 b）： 0 12 12 1 2 P 2 P + + y = h y z b z （2） 中性轴 n－n 的截距：        = − = − P 0t P 0t 6 6 z h z y h y （3） 说明中性轴 n－n，与力 FP作用点位于形心 C 的异 侧，说明 n－n 划分为 FP作用下的区域为压应力区，另 一区域是拉应力区（见图 b）。 如果将（2）改写为 1 12 12 2 P + 2 yP = − h y z b z （4） 并且把中心轴上一点（y, z）固定，即中性轴可绕该 点顺时针转动（从 1―1 转到 2―2） 由（4）式，FP 作用必沿直线移动。由（3）式，2 －2 直线的截距值大于 1－1 直线的。所以，当中性轴 1

垫电时、作用点FF沿 如果中性轴绕A点从】 -1顺时针转动至3一3（中性轴始终在截 面外周旋转)，则截面内就不产生拉应力，将A坐标代入(4)式： P+业1，即F沿该直线移动。从Fm一Fm一F,反之铅垂力 Fm→F直线路动面不产生持应力. 动的直线。这四条直线所围区域为截面核心。铅垂 压力 下会有拉应 1.己 2.求使点a处正应力为零时的角度B值， 解：M,=FolsinB,用，-b 令o,=0,则mB-务B=m一9 一0矩形面力如图所示：试 习愿7-19 求使上点正位力为时的角度的正应力 解：F=Fp.COs B ,F=601 M (a)=E sin 8x004 M,b)=2M,a,M,(d)=3M,(@) 0.1 ”-6mn -60X10(cos5°-6sin5 7 10MPa 月题7-20 o-今-2y9-gm-l2my-65m =-859MPa 2.a-ms月-12snm=0 tan B=B=4.76* 7一21交通信号灯柱上受力如图所示，灯柱为管形截面，其 外径D=200mm 解：tam6=32 ,0=22.62 7.8 =-40+900+1950s -6700 M=1950sim8x(7.8-06-900x21=3510N·m 2-0912M 6700 里定 习题721图 66

— 66 — 习题 7-19 图 z y A 1 2 3 2 B F P1 F P2 F P3 F 3 (d) 习题 7-20 图 习题 7-21 图 －1 顺时针转向中性轴 2－2 时，FP作用点 FP1、FP2沿 直线，并绕形心也顺时针转向。 如果中性轴绕 A 点从 1―1 顺时针转动至 3―3（中性轴始终在截 面外周旋转），则截面内就不产生拉应力，将 A 坐标代入（4）式： 1 6 6 P P + = h y b z ，即 FP 沿该直线移动。从 FP1→FP2→FP3，反之铅垂力 FP从 FP1→FP2→FP3 直线移动，截面不产生拉应力，同理过 B、F、D 分别找另三条 FP移动的直线。这四条直线所围区域为截面核心。铅垂 压力在截面核心内作用，则横截面上不会有拉应力。 7－19 矩形截面悬臂梁受力如图所示，其中力 FP的作用线通过截面形心。试： 1．已知 FP、b、h、l 和  ，求图中虚线所示截面上点 a 的正应力； 2．求使点 a 处正应力为零时的角度  值。 解： M y = FP lsin  ， 6 2 hb Wy = Mz = FP l cos  ， 6 2 bh Wz = ( cos sin ) 6 2 2 P  b  h  b h lF W M W M y y z z a = − = − 令  a = 0 ，则 h b tan  = ， h 1 b tan −  = 7－20 矩形截面柱受力如图所示。试： 1．已知  = 5°，求图示横截面上 a、b、c 三点的正应力。 2．求使横截面上点 b 正应力为零时的角度  值。 解： FNx = FP cos  M y (a) = FP sin  0.04 M (b) 2M (a) y = y ， M (c) 3M (a) y = y 1． 6 0.1 0.04 0.04 sin 0.1 0.04 cos 2 N P P  −  = − =    F F W M A F y x y a (cos5 6sin5 ) 0.004 60 10 (cos 6sin ) 0.1 0.04 3  −   = −  =   FP = 7.10 MPa (cos5 12sin 5 ) 0.745 0.004 2 ( ) 60 103 N  −  = −  = − = y x y b W M a A F  MPa 8.59 3 ( ) N = − = − y x y c W M a A F  MPa 2． (cos 12sin ) 0 N  =  −  = A F x b 12 1 tan  = ，  = 4.76° 7－21 交通信号灯柱上受力如图所示。灯柱为管形截面，其 外径 D = 200mm，内径 d = 180mm。若已知截面 A 以上灯柱的重 为 4kN。试求横截面上点 H 和 K 处的正应力。 解： 7.8 3.25 tan = ， =22.62° FNy = −(400 + 900 +1950cos) = −6700 N Mz =1950sin (7.8−0.6)−9002.1= 3510 N·m 1.12 (0.2 0.18 ) 4 π 6700 2 2 N = − − − = = A F x  H MPa

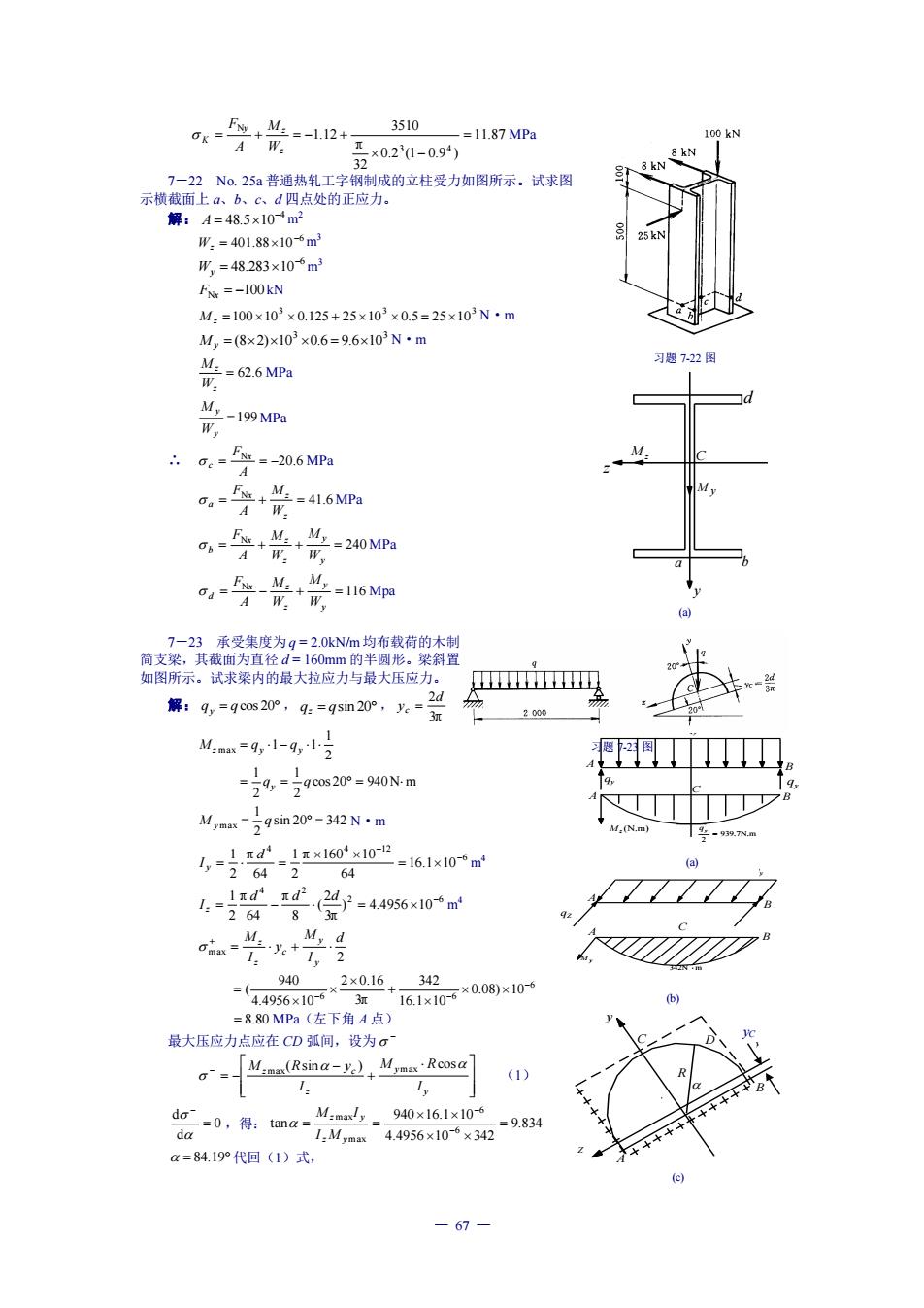
3510 =1I.87MPa x021-0.9) 7-22No.25普通热轧工字钢制成的立柱受力如图所示。试求图 形：=401.8×10*m W=48283×106m F,=-100kN M.=100×102×0.125+25×102×0.5=25×103Nm M,=(8x2x102x0.6=9.6×102N 0=626MP G==-20.6MP a-+-416Mm 解：9，=90s20°，4：=qsim20°，.=2 cmm 200 Ma"g1-g,1写 =79,=790s20°=940N.m M,an=59sim20°=342N·m 64 =16.1x10m =其-学=460 94n 2×0.16 34 =（4.4956x10 3知 16.1x10×0.08)x10 =8.8OMPa(左下角A点 最大压应力点应在CD弧间，设为G a=M:ma(Rsina-y)Myma Rcosa (1) -0，得ma= M.I. 940×161×10-6 44956x10×32=9834 a=84.19°代回(1)式 67

— 67 — A B qZ qZ A C B M y 342N  m qy (b) A B qy qy A B C (N.m) M z 939.7N.m 2 = qy qy (a) 习题 7-22 图 d C a b z M z M y y (a) 习题 7-23 图 C D Z R  C y B A y C (c) 11.87 0.2 (1 0.9 ) 32 π 3510 1.12 3 4 N =  − = + = − + z y z K W M A F  MPa 7－22 No. 25a 普通热轧工字钢制成的立柱受力如图所示。试求图 示横截面上 a、b、c、d 四点处的正应力。 解： 4 48.5 10− A =  m 2 6 401.88 10 − Wz =  m 3 6 48.283 10− Wy =  m 3 FNx = −100 kN 3 3 3 M z =100 10  0.125 + 2510  0.5 = 2510 N·m 3 3 M y = (82)10 0.6 = 9.610 N·m = 62.6 z z W M MPa =199 y y W M MPa ∴ 20.6 N = = − A F x  c MPa 41.6 N = + = z x z a W M A F  MPa 240 N = + + = y y z x z b W M W M A F  MPa 116 N = − + = y y z x z d W M W M A F  Mpa 7－23 承受集度为 q = 2.0kN/m均布载荷的木制 简支梁，其截面为直径 d = 160mm 的半圆形。梁斜置 如图所示。试求梁内的最大拉应力与最大压应力。 解： q = q cos 20 y ， q = qsin 20 z ， 3π 2d yc = cos 20 940N m 2 1 2 1 2 1 max 1 1 = =  =  =  −   q q M q q y z y y sin 20 342 2 1 M y max = q  = N·m 6 4 4 12 16.1 10 64 π 160 10 2 1 64 π 2 1 − − =    =  = d I y m 4 2 6 4 2 ) 4.4956 10 3π 2 ( 8 π 64 π 2 1 − = −  =  d d d I z m 4 2 max d I M y I M y y c z z =  +  +  6 6 6 0.08) 10 16.1 10 342 3π 2 0.16 4.4956 10 940 ( − − −    +    = = 8.80 MPa（左下角 A 点） 最大压应力点应在 CD 弧间，设为 −           + − = − − y y z z c I M R I M R  y   ( sin ) max cos max （1） 0 d d = −   ，得： 9.834 4.4956 10 342 940 16.1 10 tan 6 6 max max =     = = − − z y z y I M M I   = 84.19 代回（1）式， yC