《材料力学》课程教学资源（学习资料）材料力学知识一览图（可复制）

基本概念：荷载（静荷载、动荷载】，盟度、刚度、稳定性，可变形四体及基本假设，杆及几何特在，内力，应力正应力、切应力】，应变（线应变、切应变】。截面几何性质（静矩、惯性矩、惯性半径、板惯性矩，平行移轴公式】 简化、分解 力（香直于轴线）、力偶 组合变形：分析步囊与基本变形同。 1、外力分析 力。作用线与轴线重合 力偶。作用直与轴线垂直 平衡分析 作用在含牡线的纵向平面内 拉压与弯曲组合、两垂直平面内膏曲组合：横就面上最 大正应力的点处于单轴应力状态。 高扭组合变形：横截面上正应力最大的点处，扭转切应 静定 轴向拉压 扭转（轴） 弯西（梁.对称弯曲） 力也最大，处于平芭虚力状态。 补充方程 超静定 列方程作图： 连接件的实用计算 轴力Fw(拉为正.压为负) 扭矩丁（右手螺旋判正负】 剪力F(左上右下为正) 藏面法 挤压面：香直于外力 2、内力分析 扭矩图 弯矩M(左顺右逆为正) 利用微分关系些-华些5零、平、斜、抛： (裁、代、平) 轴力图 剪力图、高矩图 方向（受力非均匀时 叠加法作图。 取其正投影：直径平 Fwx(等直杆】 Tam(等直轴) 二·山（横载面关于中性轴非对称） ) 绘截面及其内力 (横数面关于中性蛙对称)： F、较大且载应较小（变裁面杆） T较大且扭转数面系数较小（变裁面轴） 挤压力：由被连接件 的平衡分析得到 剪切面：发生相对错 几何关系 模裁面上： 横酸面上：。.y 动的面，与外力平 3、应力分析 物理关系 横黄面上： 行。 静力学关系 A 边缘处 剪力：连接件采用裁 离中性轴最远处：。一4》一一4（对称酸面） 面法分析得到。 危险点及其 就取单元体 斜裁面上： 0n■cra 斜裁面上： 应力状态 (初始用横、额数面) 中性特处：5一（等直梁）：手5（矩形：而） Tan =T-G12 a■i 2 bi ra=Tg■r 非最远又张守性轴处：C,: 单轴虚力状态 纯剪切状态 解析法、应力圆法 单轴应力状态 纯剪切状态 平面应力状态 确定斜截面上应力、 主应力、主平面、主 胡克定律a一Er 胡克定律：T■G7 相对扭转角- I M 挠曲线近似数分方程：E■-M(x) 单元体 变形分析 变形量W. G, p EI E T 绕度 积分法：边界条件（约束条件、连续条件】 节点位移：切线代圆弧 单位长度扭转角可■ Gl, 转角0-w 叠加法（逐段刚化法） 能量法求内力成变形： T 广义胡克定律 应变能： 功能原理F一：成卡氏定理 应支能：-品血 应支能密度：% 应变能密度：一三可 应变能密度：。=0 材科的力学性能：拉压、（扭转）、弯曲标准试验。塑性材料、能性材料的特征。低碳钢性能参数，可云6、y:铸铁Gdv:无明显园服阶段的塑性材料σ 4、强度计算 单物应力状态：as小纯剪切状态：。可·平面应力状态：a,s口]：常温、静栽下，四个常用强度理论：第一， 二适用于脆性断裂，第三、四适用于塑性屈服。 别度计算 刚度条件：扭转： 单位长度细转角以个，等直圆轴登x旷个等鱼：丹sg 换鱼线近似微分方程+边界条件一细长杆临界力欧拉公式厂·识 稳定计算压杆)】 们计算柔度2-出2)判断轩的类型计算临界应力：2之人，.- ；As2c,经验公式：2c,a.-G,(3l稳定条件：c-三sL,稳定安全因数cL-:稳定因数cL-Gp=p小

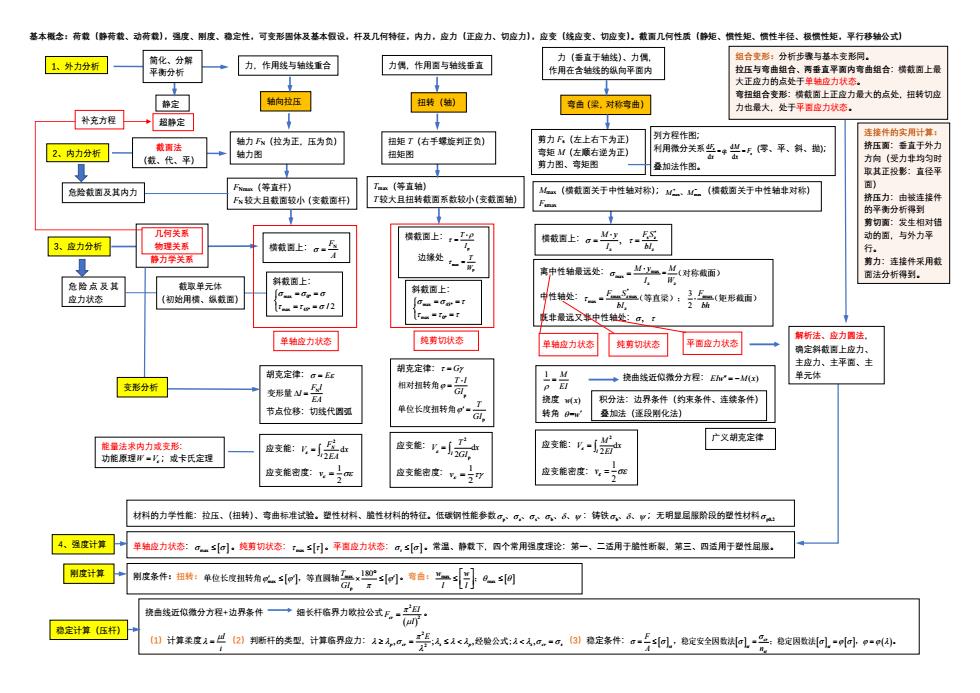
基本概念：荷载（静荷载、动荷载），强度、刚度、稳定性，可变形固体及基本假设，杆及几何特征，内力，应力（正应力、切应力），应变（线应变、切应变）。截面几何性质（静矩、惯性矩、惯性半径、极惯性矩，平行移轴公式） 1、外力分析 2、内力分析 3、应力分析 4、强度计算 刚度计算 材料的力学性能：拉压、（扭转）、弯曲标准试验。塑性材料、脆性材料的特征。低碳钢性能参数       p e s b 、 、 、 、 、 ：铸铁    b、 、 ；无明显屈服阶段的塑性材料  p0.2 能量法求内力或变形： 功能原理 W V=  ；或卡氏定理 稳定计算（压杆） 力，作用线与轴线重合 轴向拉压 扭转（轴） 弯曲（梁，对称弯曲） 力偶，作用面与轴线垂直 力（垂直于轴线）、力偶， 作用在含轴线的纵向平面内 静定 超静定 剪力 Fs（左上右下为正） 弯矩 M（左顺右逆为正） 剪力图、弯矩图 FNmax（等直杆） FN 较大且截面较小（变截面杆） Tmax（等直轴） T较大且扭转截面系数较小（变截面轴） 截面法 （截、代、平） 几何关系 物理关系 静力学关系 横截面上： FN A  = 危 险 点 及 其 应力状态 单轴应力状态 补充方程 截取单元体 （初始用横、纵截面） 斜截面上： max 0 max 45 / 2          = =   = = 横截面上： p T I    = 边缘处 max p T W  = 纯剪切状态 斜截面上： max 45 max 0          = =   = = 横截面上： * s z z , M y F Sz I bI    = = 离中性轴最远处： max max z z M y M I W   = = （对称截面） 中性轴处： * smax max smax max z 3 2 F S F z bI bh  =  （等直梁）； （矩形截面） 既非最远又非中性轴处：   , 单轴应力状态 纯剪切状态 平面应力状态 胡克定律：   = E F l N l EA 变形量  = 节点位移：切线代圆弧 胡克定律：   = G p T l GI   相对扭转角 = p T GI 单位长度扭转角 = 1 M  EI = 挠曲线近似微分方程： EIw M x  = − ( ) 挠度 w x( ) 积分法：边界条件（约束条件、连续条件） 转角  =w  叠加法（逐段刚化法） 应变能： 2 d 2 N l F V x EA  =  应变能密度： 1 2 v =  应变能： 2 p d l 2 T V x GI  =  应变能密度： 1 2 v =  应变能： 2 d l 2 M V x EI  =  应变能密度： 1 2 v =  单轴应力状态：   max    。纯剪切状态：   max    。平面应力状态：   r   。常温、静载下，四个常用强度理论：第一、二适用于脆性断裂，第三、四适用于塑性屈服。 刚度条件：扭转：     max max p T 180 GI      单位长度扭转角       ，等直圆轴 。弯曲：   max max w w l l          ； 挠曲线近似微分方程+边界条件 细长杆临界力欧拉公式 ( ) 2 cr 2 EI F l   = 。 （1）计算柔度 l i   = （2）判断杆的类型，计算临界应力： 2 2 , ; , , p cr s p s cr s  E             =    = 经验公式; （3）稳定条件：         ( ) cr st st st st F A n           =  = = = ，稳定安全因数法 ；稳定因数法 ， 。 简化、分解 平衡分析 轴力 FN（拉为正，压为负） 轴力图 扭矩 T（右手螺旋判正负） 扭矩图 危险截面及其内力 变形分析 Mmax（横截面关于中性轴对称）； M M max max + − 、 （横截面关于中性轴非对称） Fsmax 连接件的实用计算： 挤压面：垂直于外力 方向（受力非均匀时 取其正投影：直径平 面） 挤压力：由被连接件 的平衡分析得到 剪切面：发生相对错 动的面，与外力平 行。 剪力：连接件采用截 面法分析得到。 列方程作图； 利用微分关系 d d d d s s F M q F x x = = ； (零、平、斜、抛)； 叠加法作图。 解析法、应力圆法， 确定斜截面上应力、 主应力、主平面、主 单元体 组合变形：分析步骤与基本变形同。 拉压与弯曲组合、两垂直平面内弯曲组合：横截面上最 大正应力的点处于单轴应力状态。 弯扭组合变形：横截面上正应力最大的点处，扭转切应 力也最大，处于平面应力状态。 广义胡克定律