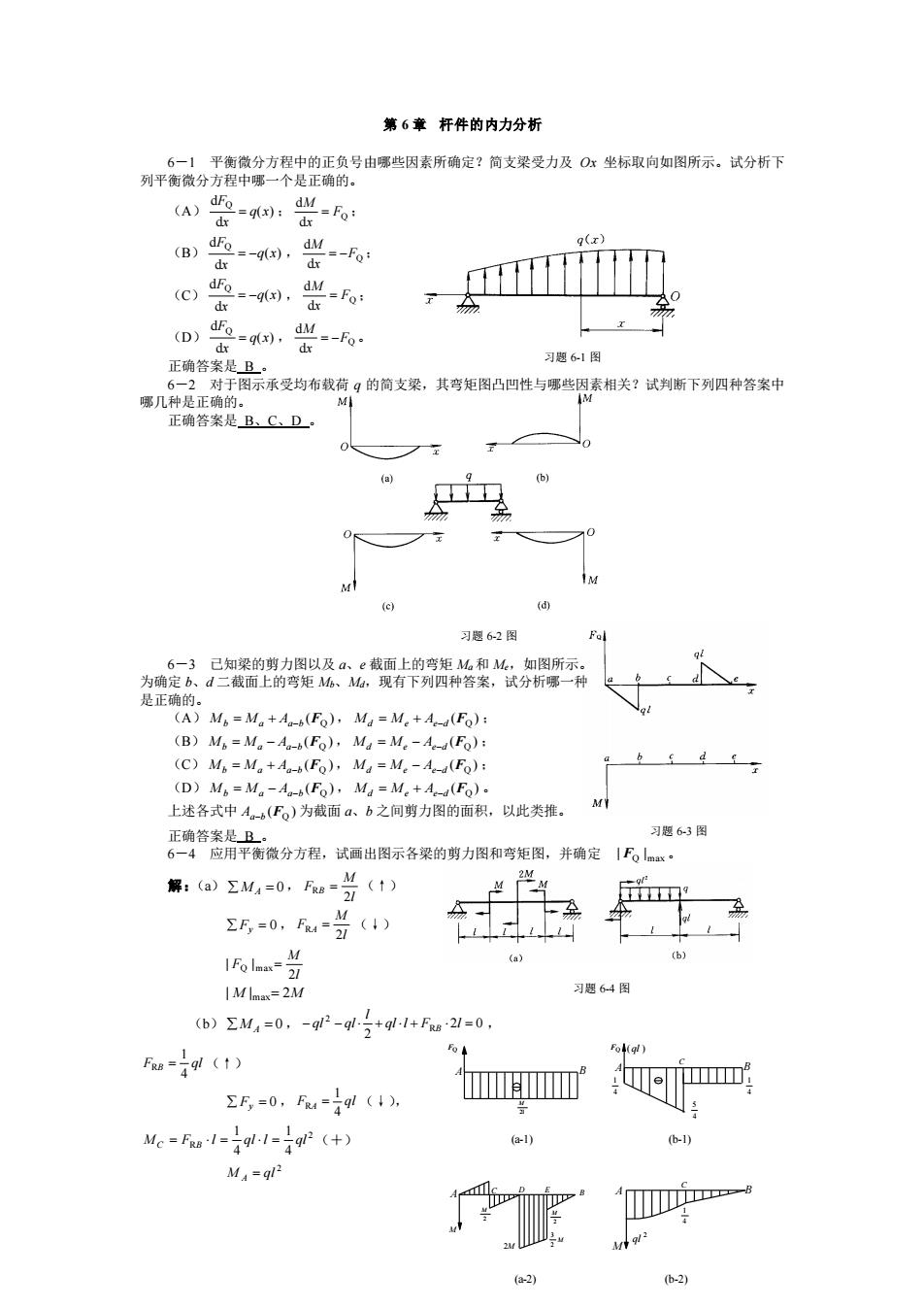
第6章杆件的内力分析 的正负号由哪些因素所确定?简支梁受力及O坐标取向如图所示。试分析下 习题61图 9的简支梁,其弯矩图凸四性与哪些因素相关?试判断下列四种答案中 正确答案是B、C、D· 0 (b) 习题62图 是正确的: M=M。+A(Eo),M=M+AE) (B)M=M-A(Fo),Ma=M.-4(Fo) (C)M,=M+A(Fo),Ma =M.-A(Fo) (D)M。=M。-A-(Fo),M4=M.+A-(Fa). 上述各式中A-(F)为截面a、b之间剪力图的面积,以此类推, 费香整指品福分方积.酒际者笑的药力用鸟能,并精定1万儿 习题6-3图 解:(a)M=0,Fs=(t) ,=0,u=岁(4) IFo lme (b) =2M 习思64图 (b)ΣM=0,-g2-9+g-1+Fw21=0 F=19(t) EE,=0,Fu=19l(1 女om Me-Fu1-91-g2(+) e M,=92 -2) b-2)
— 50 — 习题 6-1 图 习题 6-2 图 习题 6-3 图 习题 6-4 图 A B A B C (ql ) 2l M FQ FQ 4 5 4 1 4 1 (a-1) (b-1) A C D E M A B C M B 2M 2MM 2 3 4 1 2M 2 ql (a-2) (b-2) 第 6 章 杆件的内力分析 6-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及 Ox 坐标取向如图所示。试分析下 列平衡微分方程中哪一个是正确的。 (A) ( ) d d Q q x x F = ; Q d d F x M = ; (B) ( ) d d Q q x x F = − , Q d d F x M = − ; (C) ( ) d d Q q x x F = − , Q d d F x M = ; (D) ( ) d d Q q x x F = , Q d d F x M = − 。 正确答案是 B 。 6-2 对于图示承受均布载荷 q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中 哪几种是正确的。 正确答案是 B、C、D 。 6-3 已知梁的剪力图以及 a、e 截面上的弯矩 Ma 和 Me,如图所示。 为确定 b、d 二截面上的弯矩 Mb、Md,现有下列四种答案,试分析哪一种 是正确的。 (A) ( ) Mb = Ma + Aa−b FQ , ( ) Md = Me + Ae−d FQ ; (B) ( ) Mb = Ma − Aa−b FQ , ( ) Md = Me − Ae−d FQ ; (C) ( ) Mb = Ma + Aa−b FQ , ( ) Md = Me − Ae−d FQ ; (D) ( ) Mb = Ma − Aa−b FQ , ( ) Md = Me + Ae−d FQ 。 上述各式中 ( ) Aa−b FQ 为截面 a、b 之间剪力图的面积,以此类推。 正确答案是 B 。 6-4 应用平衡微分方程,试画出图示各梁的剪力图和弯矩图,并确定 Q max | F | 。 解:(a) M A = 0 , l M F B 2 R = (↑) Fy = 0, l M F A 2 R = (↓) l M F 2 | Q |max = | M |max = 2M (b) M A = 0 , 2 0 2 R 2 − − + ql l + F l = l ql ql B , F ql B 4 1 R = (↑) Fy = 0 , F ql A 4 1 R = (↓), 2 R 4 1 4 1 M F l ql l ql C = B = = (+) 2 M ql A =

IFo IML=al (c)ΣF,=0,F4=gl(1) M,=0,M4=g Mn=0,g2+g1-gMn=0 四 Mo-3qr IFo l-q! e (d)∑MB=0 fu-21-g9g11=0 Fu-iql (1) ΣR,-0,e=gl(t d ΣMg=0,Mg=号 ΣM。=0,Mo=爱g2 IF wL-克gr 证 (e)ΣE,=0,F=0 (42) EMc=0.-ql-1+ql+Mc-0 Me-ql2 四/ ΣM。=0,Ma=-5g W ΣF=0,Fas=g IFo lmax=ql IM lm=gl2 (DΣM,=0,Fs=9(t) ΣF,=0,F4=79l(1) Lh EF,=0.-791+ql-For=0 (1) Fos-ql 工Mo=0,0片9吃Mo=0 Mo-sal (-2 Me-sql IFo lna=
— 51 — (c) (d) A D B C 1 1.5 1 ( ) 2 M ql ( ) 2 M ql A D B C 32 25 2 1 (c-2) (d-2) (e) (f) A B C 0.5 B E C 0.5 0.5 D ql FQ FQ ql (e-1) (f-1) B C 1 0.5 ( ) 2 M ql A (e-2) (a) (b) A D B C l A D B C 1 0.75 FQ FQ 1.25 1 (c-1) (d-1) (gl) (gl) A C D B 0.125 E 0.125 ( ) 2 M ql (f-2) F ql 4 5 | Q |max = 2 max | M | = ql (c) Fy = 0 , F ql RA = (↑) M A = 0 , 2 M ql A = MD = 0, 0 2 2 + − − M D = l ql ql l ql 2 2 3 M ql D = F max = ql Q | | 2 max 2 3 | M | = ql (d) MB = 0 0 2 1 FRA 2l − q 3l − ql l = F ql A 4 5 R = (↑) Fy = 0 , F ql B 4 3 R = (↑) MB = 0 , 2 2 l q M B = MD = 0, 2 32 25 M ql D = F ql 4 5 | Q |max = 2 max 32 25 | M | = ql (e) Fy = 0 ,FRC = 0 MC = 0 , 0 2 2 3 − + + M C = l ql l ql 2 M ql C = MB = 0 , 2 2 1 M ql B = Fy = 0 , F ql QB = F max = ql Q | | 2 max | M | = ql (f) MA = 0 , F ql B 2 1 R = (↑) Fy = 0 , F ql A 2 1 R = (↓) Fy = 0 , 0 2 1 − ql + ql − FQB = F ql B 2 1 Q = MD = 0, 0 2 2 2 4 1 − + M D = l l q l ql 2 8 1 M ql D = − 2 8 1 M ql E = ∴ F ql 2 1 | Q |max = 2 M 2 M
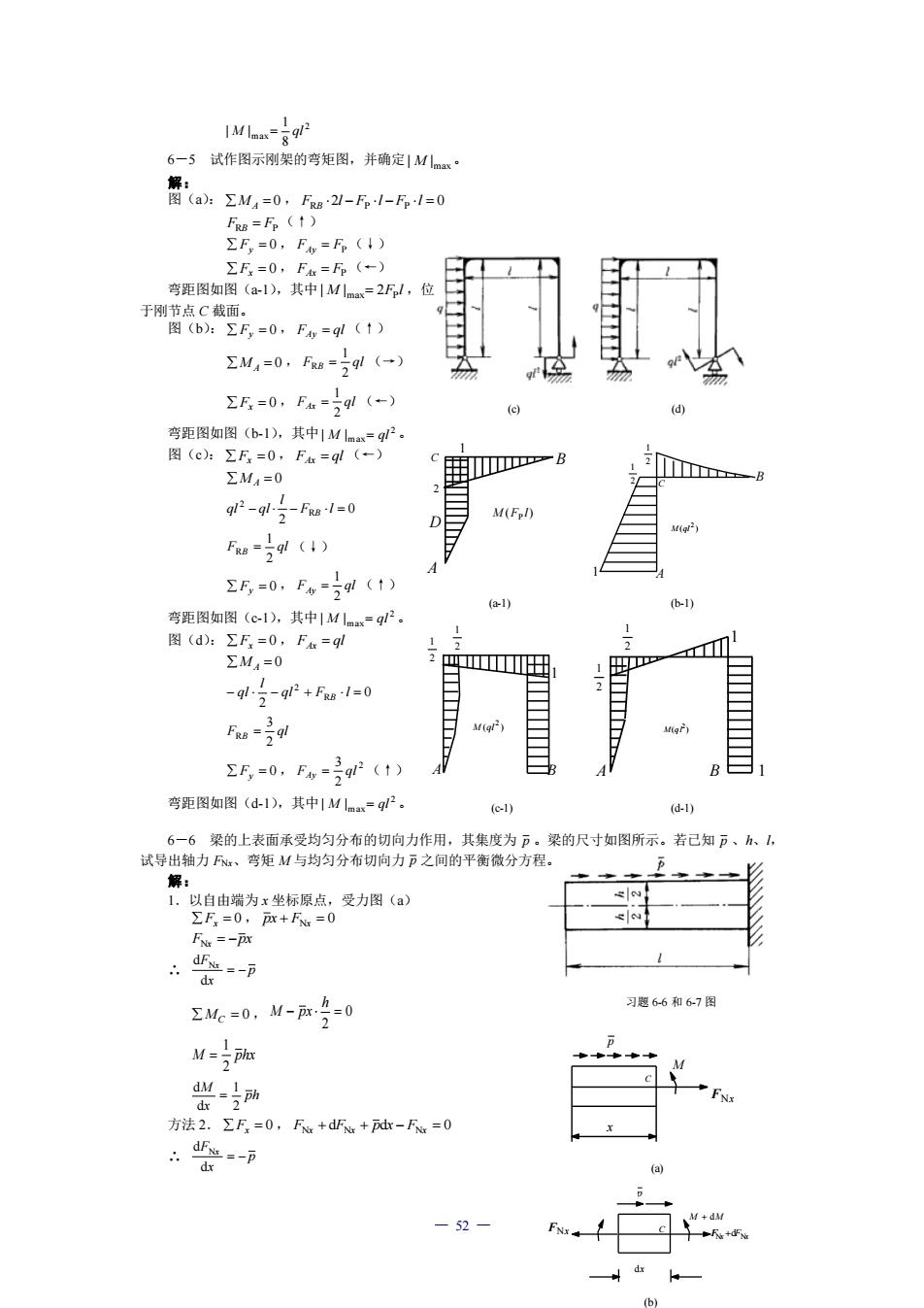
IMln-ol 6一5试作图示刚架的弯矩图,并确定|M1m 圆2w,-0,-5-61e0 Fu=(↑) ΣF=0,F6=F(4) ∑F=0,F=Fp(+) 弯距图如图(a1),其中|Ml=2F,位 ΣM,=0,FR=9l(-) 2R=0,Fa=0(-) 弯距图如图(b-1),其中1M1ma=g2 图(c片ΣR=0,F=gl(-) ∑M4=0 g2-g1-fF1=0 M(Fpl D F=g() 25=0.Fw=590(1) 弯距图如图(e.其中1L一g。 e1 b1 -ql-q+Fw:I-0 Faa-3gl g ΣF=0,F=92(1) 弯距图如图(d-1).其中1M1o=g产. (c-1) d-) 生盟电。 ΣMe=0,M-9=0 习题66和6-7图 M=plx w=动 方法2.Σ万=0,F+d+随-=0 -52
— 52 — 2 1 2 1 A B 1 1 (d-1) 2 1 2 1 A B 1 ( ) 2 M ql (c-1) 2 1 2 1 C B 1 A ( ) 2 M ql (b-1) FNx Nx FNx F +d C M + dM dx p (b) M FNx x C p (a) (c) (d) C B A D 2 ( ) P M F l 1 (a-1) 习题 6-6 和 6-7 图 2 max 8 1 | M | = ql 6-5 试作图示刚架的弯矩图,并确定 max | M | 。 解: 图(a): MA = 0 , FRB 2l −FP l −FP l = 0 FRB = FP (↑) Fy = 0 , FAy = FP (↓) Fx = 0 , FAx = FP (←) 弯距图如图(a-1),其中 M F l max 2 P | | = ,位 于刚节点 C 截面。 图(b): Fy = 0 , F ql Ay = (↑) MA = 0 , F ql B 2 1 R = (→) Fx = 0 , F ql Ax 2 1 = (←) 弯距图如图(b-1),其中 2 max | M | = ql 。 图(c): Fx = 0 , F ql Ax = (←) MA = 0 0 2 R 2 − − F l = l ql ql B F ql B 2 1 R = (↓) Fy = 0 , F ql Ay 2 1 = (↑) 弯距图如图(c-1),其中 2 max | M | = ql 。 图(d): Fx = 0 , F ql Ax = MA = 0 0 2 R 2 − − ql + F l = l ql B F ql B 2 3 R = Fy = 0 , 2 2 3 F ql Ay = (↑) 弯距图如图(d-1),其中 2 max | M | = ql 。 6-6 梁的上表面承受均匀分布的切向力作用,其集度为 p 。梁的尺寸如图所示。若已知 p 、h、l, 试导出轴力 FNx、弯矩 M 与均匀分布切向力 p 之间的平衡微分方程。 解: 1.以自由端为 x 坐标原点,受力图(a) Fx = 0 , px + FNx = 0 F px Nx = − ∴ p x F x = − d d N MC = 0 , 0 2 − = h M px M phx 2 1 = ph x M 2 1 d d = 方法 2. Fx = 0 , FNx + dFNx + pdx − FNx = 0 ∴ p x F x = − d d N ( ) 2 M ql
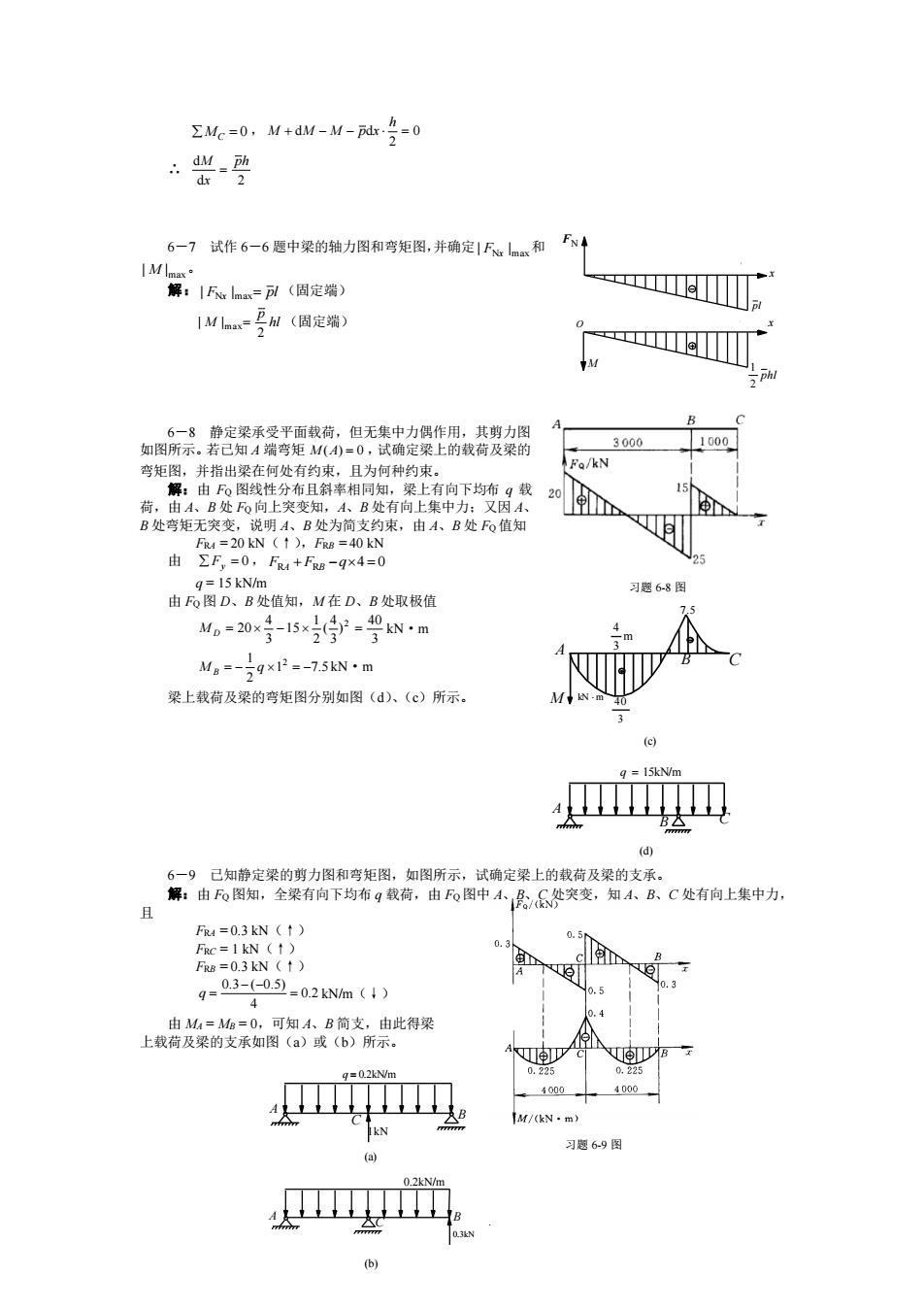
ΣMe=0,M+dM-M-tg-0 兴必 6一7试作6一6愿中梁的轴力图和弯矩图,并确定1Kl和十 解:1K=(固定端) e IMln=号l(固定端) 茶碧容器来紧,无餐定复作的取数黎钢 3000 1000 弯矩 Fa/kN 。线性分布华相同,架有向下均9载 ,F+Fs-qx4=0 由0图D、B处值知,M在D、B处取极值 习题6-8图 M。=20号15x=9Nm M。=-gxP=-7.5kN·m 梁上载荷及梁的弯矩图分别如图(d)、(c)所示。 d c有中 FR=0.3kN(↑) Fa=0.3kN(1) g=03-=02N() 习题69图 (al
— 53 — A B C 0.2kN/m 0.3kN (b) A B C q = 15kN/m (d) FN x l l x phl 2 M 1 O pl A M m 3 4 3 40 B C 7.5 kN m (c) 习题 6-8 图 习题 6-9 图 A B C q = 0.2kN/m 1kN (a) MC = 0 , 0 2 + d − − d = h M M M p x ∴ d 2 d ph x M = 6-7 试作 6-6 题中梁的轴力图和弯矩图,并确定 N max | | F x 和 max | M | 。 解: F pl | Nx |max = (固定端) hl p M 2 | |max = (固定端) 6-8 静定梁承受平面载荷,但无集中力偶作用,其剪力图 如图所示。若已知 A 端弯矩 M (A) = 0 ,试确定梁上的载荷及梁的 弯矩图,并指出梁在何处有约束,且为何种约束。 解:由 FQ 图线性分布且斜率相同知,梁上有向下均布 q 载 荷,由 A、B 处 FQ 向上突变知,A、B 处有向上集中力;又因 A、 B 处弯矩无突变,说明 A、B 处为简支约束,由 A、B 处 FQ 值知 FRA = 20 kN(↑),FRB = 40 kN 由 Fy = 0 , FRA + FRB −q4 = 0 q = 15 kN/m 由 FQ 图 D、B 处值知,M 在 D、B 处取极值 3 40 ) 3 4 ( 2 1 15 3 4 20 2 M D = − = kN·m 1 7.5 2 1 2 M B = − q = − kN·m 梁上载荷及梁的弯矩图分别如图(d)、(c)所示。 6-9 已知静定梁的剪力图和弯矩图,如图所示,试确定梁上的载荷及梁的支承。 解:由 FQ 图知,全梁有向下均布 q 载荷,由 FQ 图中 A、B、C 处突变,知 A、B、C 处有向上集中力, 且 FRA = 0.3 kN(↑) FRC = 1 kN(↑) FRB = 0.3 kN(↑) 0.2 4 0.3 ( 0.5) = − − q = kN/m(↓) 由 MA = MB = 0,可知 A、B 简支,由此得梁 上载荷及梁的支承如图(a)或(b)所示
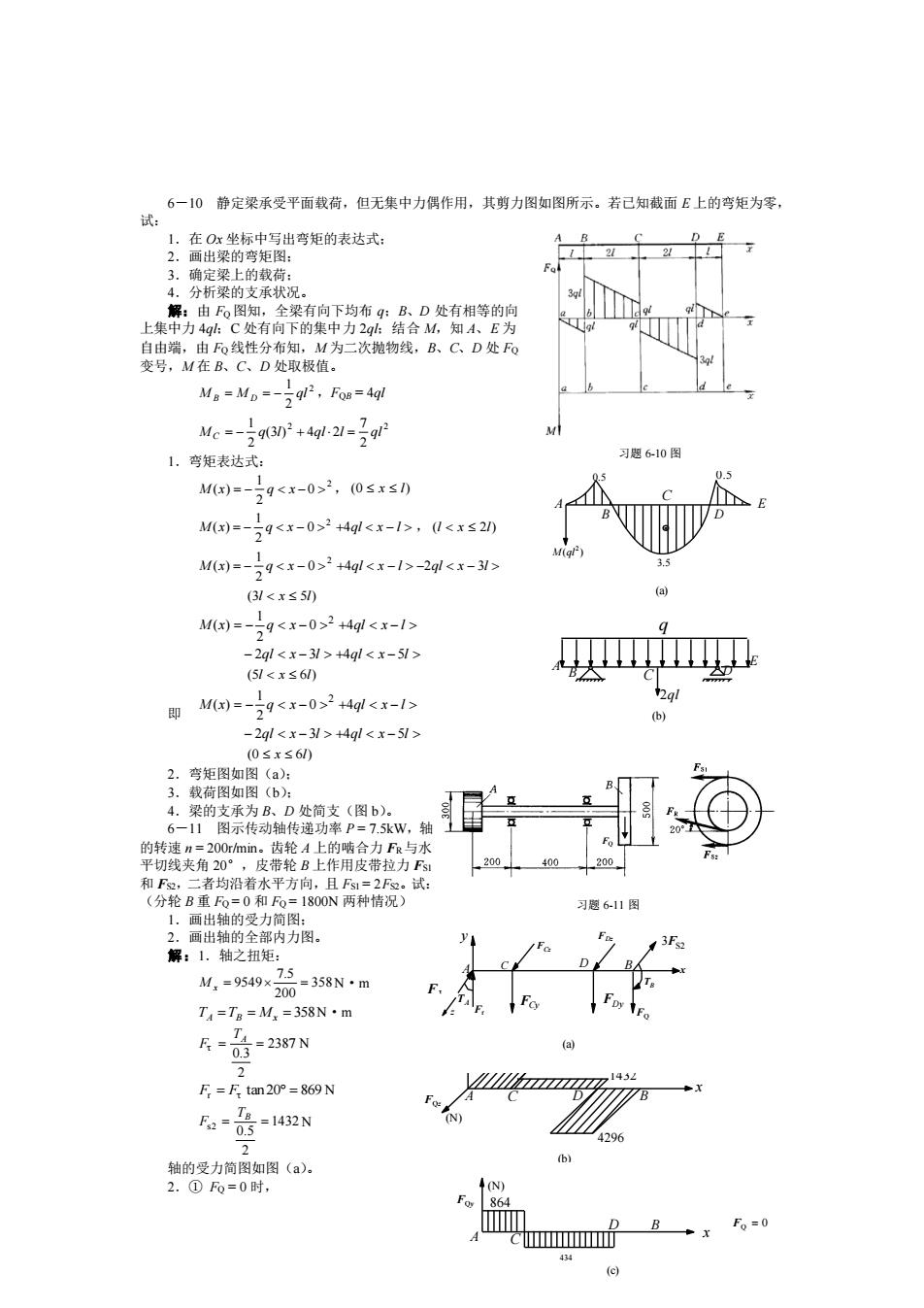
6一10静定梁承受平面载荷,但无集中力偶作用,其剪力图如图所示。若己知截面£上的弯矩为零, 试: 在O:坐标中写出弯矩的表达式: 的矩 分析梁的支承状况 F线性分布如,M为二次物线,B、C.D处 变号,M在B、C、D处取极值。 Ma =Mp=-9l-,Fos=4ql Mc=-79q302+4gl-21=791 1.弯矩表达式: 习题610图 Mx)=-q2,0≤x≤0 M)=-92+4g,02+4gl-24l M)=-592+4 2q+4q (52+4gl -2gl+4gl 0≤xs60 的支为处前图 。齿轮4上的 0”100两种情况 习题611图 解:1,轴之扭矩 M,-9549-358Nm T,=Tg=M,=358N·m 长童237N F=Ftan20°=869N 6造N 0 轴的受力简图如图(a. 2.①F%=0时, B +x=0
— 54 — A C B x y 2387 1432 4296 FQz (N) D (b) FCz A C D B FDz TB FQ TA Fr Fz S2 3F x y z (a) A C D B FQy (N) 434 864 x FQ = 0 (c) 0.5 A B C D E 0.5 3.5 ( ) 2 M ql (a) 习题 6-10 图 E C A D q 2ql B (b) FQ 习题 6-11 图 6-10 静定梁承受平面载荷,但无集中力偶作用,其剪力图如图所示。若已知截面 E 上的弯矩为零, 试: 1.在 Ox 坐标中写出弯矩的表达式; 2.画出梁的弯矩图; 3.确定梁上的载荷; 4.分析梁的支承状况。 解:由 FQ 图知,全梁有向下均布 q;B、D 处有相等的向 上集中力 4ql;C 处有向下的集中力 2ql;结合 M,知 A、E 为 自由端,由 FQ 线性分布知,M 为二次抛物线,B、C、D 处 FQ 变号,M 在 B、C、D 处取极值。 2 2 1 M M ql B = D = − ,FQB = 4ql 2 2 2 7 (3 ) 4 2 2 1 M q l ql l ql C = − + = 1.弯矩表达式: 2 0 2 1 M (x) = − q x − , (0 x l) M x = − q x − 0 +4ql x − l 2 1 ( ) 2 , (l x 2l) M x = − q x − 0 +4ql x − l −2ql x − 3l 2 1 ( ) 2 (3l x 5l) − − + − = − − + − ql x l ql x l M x q x ql x l 2 3 4 5 0 4 2 1 ( ) 2 (5l x 6l) 即 − − + − = − − + − ql x l ql x l M x q x ql x l 2 3 4 5 0 4 2 1 ( ) 2 (0 x 6l) 2.弯矩图如图(a); 3.载荷图如图(b); 4.梁的支承为 B、D 处简支(图 b)。 6-11 图示传动轴传递功率 P = 7.5kW,轴 的转速 n = 200r/min。齿轮 A 上的啮合力 FR与水 平切线夹角 20°,皮带轮 B 上作用皮带拉力 FS1 和 FS2,二者均沿着水平方向,且 FS1 = 2FS2。试: (分轮 B 重 FQ = 0 和 FQ = 1800N 两种情况) 1.画出轴的受力简图; 2.画出轴的全部内力图。 解:1.轴之扭矩: 358 200 7.5 M x = 9549 = N·m TA =TB = Mx = 358 N·m 2387 2 0.3 τ = = TA F N Fr = Fτ tan20 = 869 N 1432 2 0.5 s2 = = TB F N 轴的受力简图如图(a)。 2.① FQ = 0 时, Fτ FCy FDy

EMe =0 -0.2F+0.4F-0.6F0=0 F=434N F =0 F=-1303N =1800N时 Σe-0 F,=1254N ΣF,=0 %=-323N M=0 x=1s00N -02F-04Fk+0.3×3f=0 F=5250N E=0,Fe=1432N AN.m) AMo=0.2E=47N·m M=3f2x02=859N·m 冷W一 Fx02=173N·m =0时,M=0 e F=180N时,M=-360N·m , D F。0 0 m) 方向的晴合力分别为F=650 70试通出 图所示。若已知D 轴的受 解:1,力系向轴线简化,得受力图(a。 习题6-12图 M=650×0x101=16.25N·m M,=650x0.025=1625N·m ∑F=0,F.=650N ΣM=0,F=784N ∑F=0,F=946N EMo =0,Fe=FRe =0,Fe=F-60=325N 2.全部内力图见图(a).(b)、(c.(d)、 -55
— 55 — FNx A C B 650 (N) (b) A B Ax x F FA y FAz FBz FBy M z 650N 650N C M x y 1730N M x (a) 习题 6-12 图 A C D B x 173 360 FQ = 1800 N (N m ) M z (h) FQy A C D B x 869 546 1800 (N) FQ = 1800 N (d) A C D x 173 FQ = 0 (N m ) M z (g) (N m) M y A C D B x 477 859 (f) M x (N m) x 358 1335 (e) MCz = 0 −0.2Fr + 0.4FDy − 0.6FQ = 0 FDy = 434 N Fy = 0 FCy = −1303 N ② FQ = 1800 N 时, MCz = 0 FDy =1254 N Fy = 0 FCy = −323 N MCy = 0 −0.2Fτ − 0.4FDz + 0.33FS2 = 0 FDz = 5250 N Fz = 0, FCz =1432 N MCy = 0.2Fτ = 477 N·m MDy = 3Fs2 0.2 = 859 N·m MCz = Fr 0.2 =173 N·m FQ = 0 时, MDz = 0 FQ = 1800 N 时, MDz = −360 N·m 6-12 传动轴结构如图所示,其一的 A 为斜 齿轮,三方向的啮合力分别为 Fa = 650N,Fτ = 650N,Fr = 1730N,方向如图所示。若已知 D = 50mm,l = 100mm。试画出: 1.轴的受力简图; 2.轴的全部内力图。 解:1.力系向轴线简化,得受力图(a)。 10 16.25 2 50 650 3 = = − M x N·m Mz = 6500.025 =16.25 N·m Fx = 0 , FAx = 650 N M Az = 0 , FBy = 784 N Fy = 0 , FAy = 946 N MCy = 0 , FAz = FBz Fz = 0 , 325 2 650 FAz = FBz = = N 2.全部内力图见图(a)、(b)、(c)、(d)、 1335 C D C D z

(e)、(f)、(g)所示。 Fo(N) 784 A LJ946 (c) 7325 C Fo:(N) 325 (d) (N.m) s T (e) 325N M. (.m) 78.4 94.6 (g) -56
— 56 — A C B 325N m M y (f) A C B M x (N m ) 16.25 (e) FQy A 946 B C (N) 784 (c) A B 325 C (N) FQz 325 (d) M z (N m) A C B 94.6 78.4 (g) (e)、(f)、(g)所示