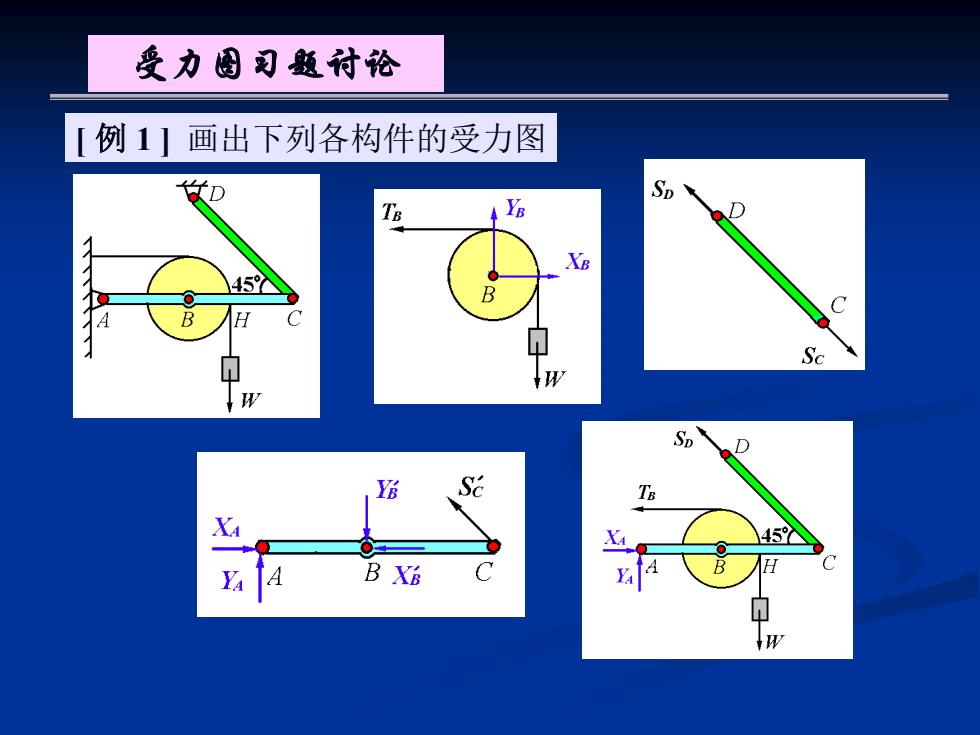
受力图习题付论 例1】画出下列各构件的受力图 女D So Ts XB 45个 ● B B Sc SD Se 459△ B XE 中
[ 例 1 ] 画出下列各构件的受力图 受力图习题讨论

[例2] 不计自重的梯子放在光滑水 平地面上,画出梯子、梯子 左右两部分与整个系统受力 图. B (a) 解: 绳子受力图如图(b)所示 整体受力图如图(e)所示 (e)
[ 例 2 ] 不计自重的梯子放在光滑水 平地面上,画出梯子、梯子 左右两部分与整个系统受力 图. 解: 绳子受力图如图(b)所示 整体受力图如图(e)所示
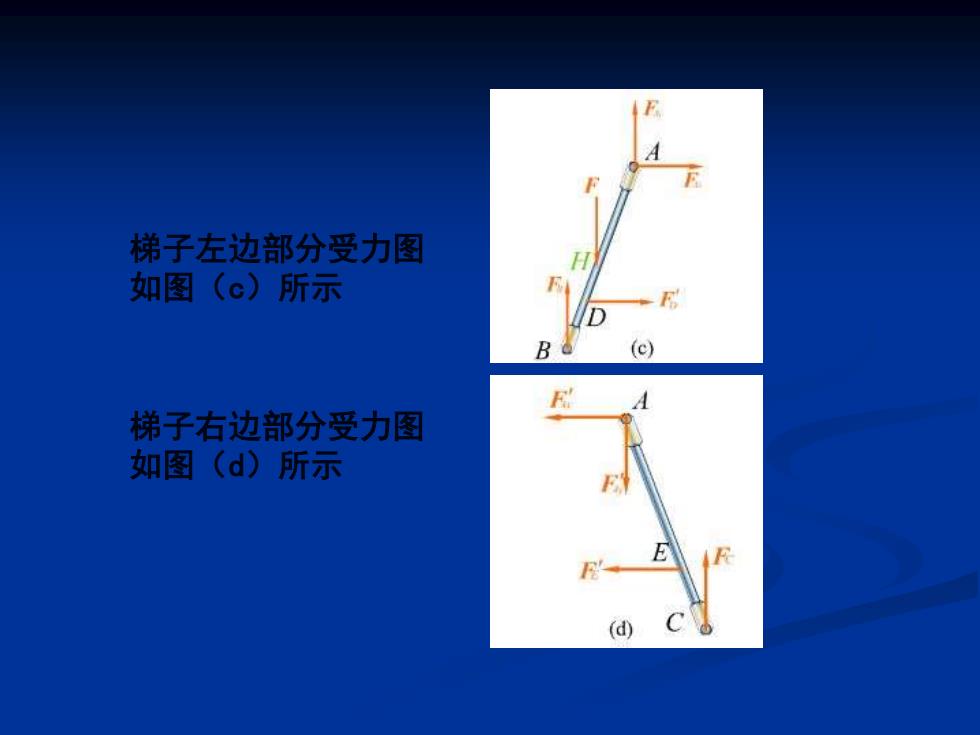
梯子左边部分受力图 如图(©)所示 c 梯子右边部分受力图 如图(d)所示 (d)
梯子左边部分受力图 如图(c)所示 梯子右边部分受力图 如图(d)所示
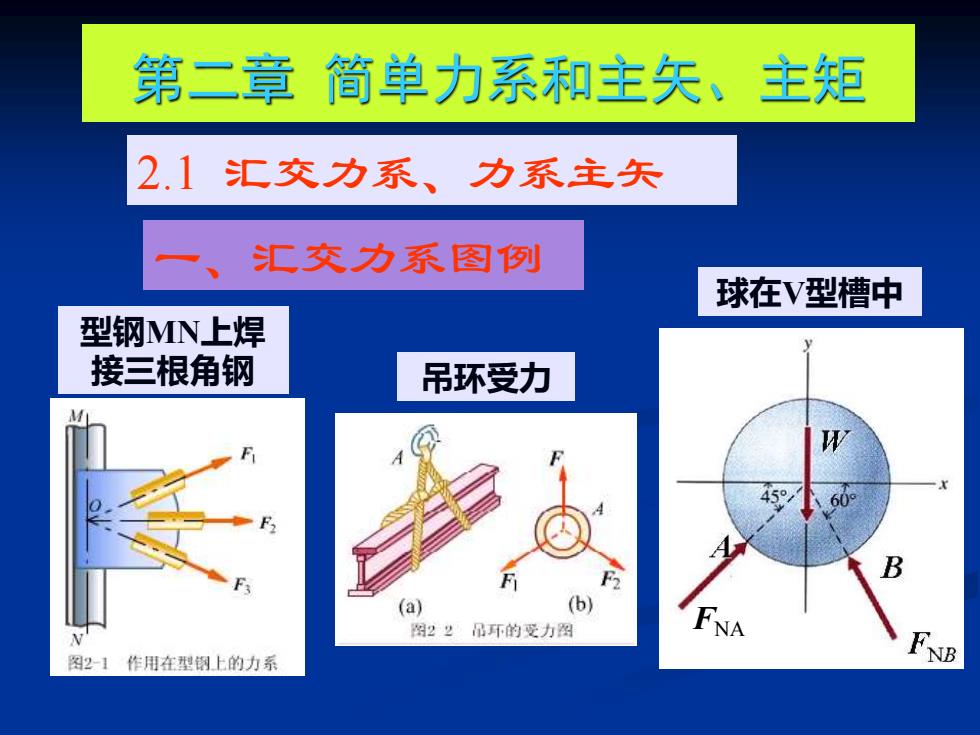
第二章简单力系和主矢、主矩 2.1汇交力系、力系主矢 E交力系图例 球在V型槽中 型钢MN上焊 接三根角钢 吊环受力 (a) (b) 图22环的受力图 图2-1作用在型钢上的力系 NB
第二章 简单力系和主矢、主矩 一、汇交力系图例 2.1 汇交力系、力系主矢 型钢MN上焊 接三根角钢 吊环受力 球在V型槽中 FNA
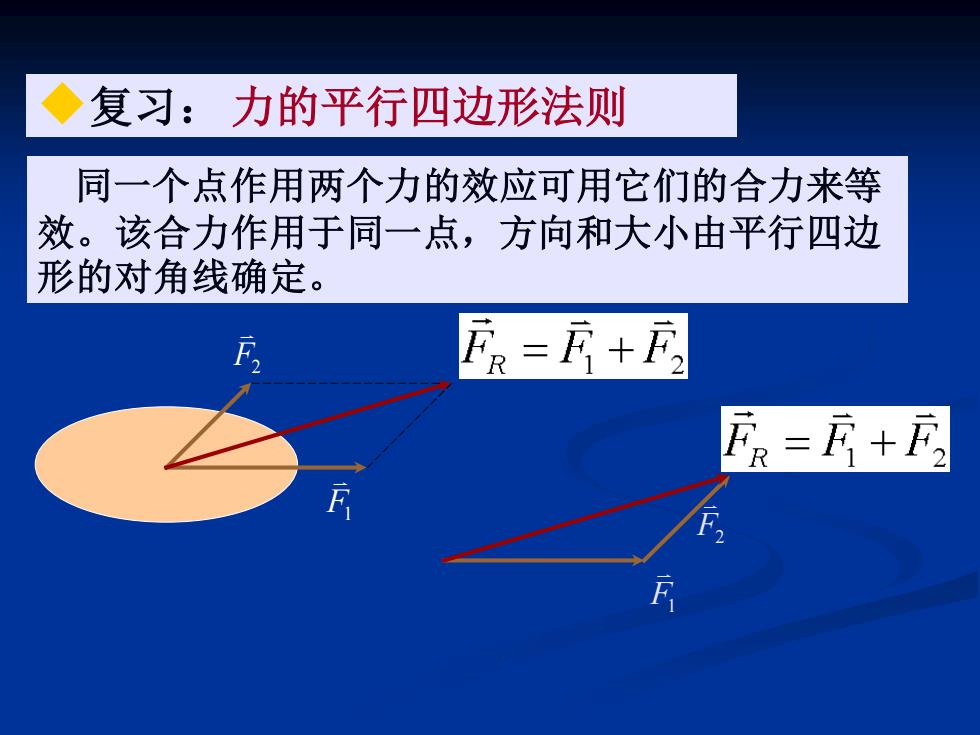
◆复习:力的平行四边形法则 同一个点作用两个力的效应可用它们的合力来等 效。该合力作用于同一点,方向和大小由平行四边 形的对角线确定。 FR=E+F2 ER=R+F2
同一个点作用两个力的效应可用它们的合力来等 效。该合力作用于同一点,方向和大小由平行四边 形的对角线确定。 ◆复习: 力的平行四边形法则 F2 F1 F1 F2

2.1.1汇交力系合成的几何法一 一力多边形法 图示F、F、B、F为刚体上平面汇交力 系沿着各力作用线搬移到汇交点A的共点力系: 合力的数学 FR=F+F2+F3+F4=∑F 表达式:
A F 2 F 1 F 4 F 3 合力的数学 表达式: FR F 1 B F 2 C F 3 D F 4 E A 图示F1、F2、F3、F4 为刚体上平面汇交力 系沿着各力作用线搬移到汇交点A的共点力系: 2.1.1 汇交力系合成的几何法— —力多边形法
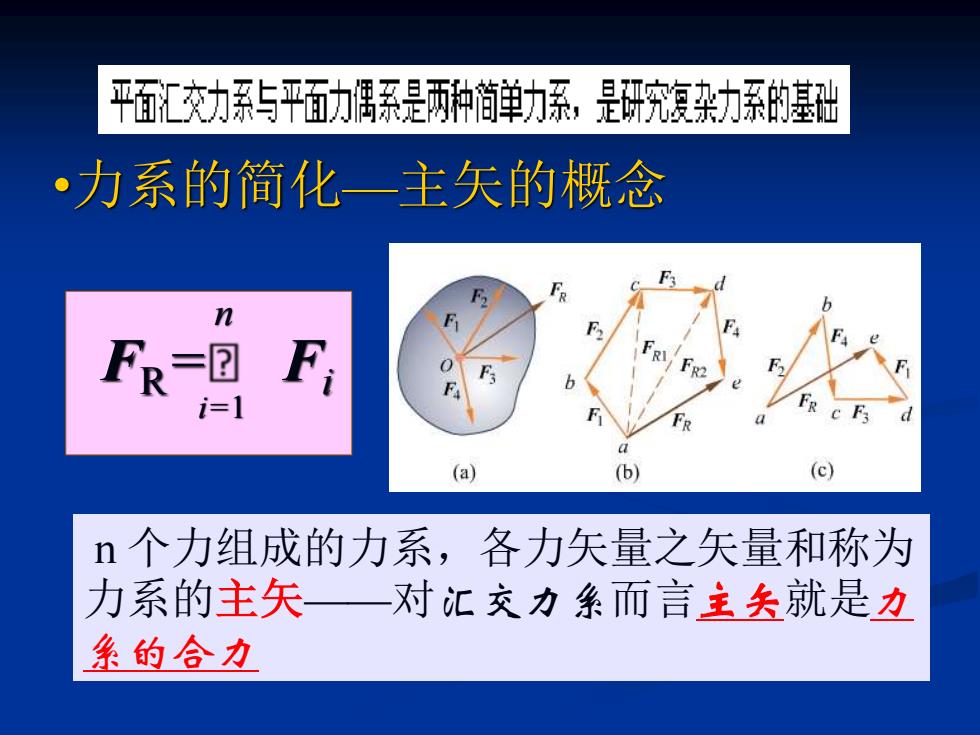
平面汇交力系5平面力偶系是两种简单力系,是研究复杂力系的基础 ·力系的简化一主矢的概念 n =回 F 1 (a) (b) (c) n个力组成的力系,各力矢量之矢量和称为 力系的主矢一对汇交力条而言主矢就是力 条的合力
FR = Fi i=1 n n 个力组成的力系,各力矢量之矢量和称为 力系的主矢——对汇交力系而言主矢就是力 系的合力 •力系的简化—主矢的概念

2.1.2力系主矢解析法 1,力的投影力沿坐标轴的分解 F=Fcos a 空间力在正交轴上的投影 F=Fcos F.=Fcosy cosa COSY= F 2、力的解析表达式 =VF2+F+F F F=Fi+F,·j+F。k
2.1.2 力系主矢解析法 1、力的投影.力沿坐标轴的分解 2、力的解析表达式

3,力在坐标轴上投影的二次投影法: F.=Fcos0 Fw=Fsin9 XV cos o ℉,=Fw·sinp F=F cos=Fsin0.cos F=Fsin=Fsin.sin
3、力在坐标轴上投影的二次投影法:

2-1-1、力系主矢的计算公式 F=Fi+F,·j+FR Fe=FRi+FR·j+FR·k =∑方 i=1 n n FR=昌FxFs闾Fy FR F i=1 FR=VEx)+(FR}+(ER:)》 cosa -cos?= F咫 方向余弦
2-1-1、力系主矢的计算公式 FRx = Fix i=1 n FRy = Fiy i=1 n i=1 n FRz = Fi z 方向余弦