
2-3.任意力系的简化
2-3. 任意力系的简化

2-3-1力向一点平移定理 1.实例
2024-10-1 F F-F F
2、力线平移定理: 把力F作用线向某点0平移时,必须附加一 个力偶,此附加力偶矩的大小等于原力F对平移 点0的力矩。 证明: F'=-F"=F M=Fd =mo(F) 2024-10-1
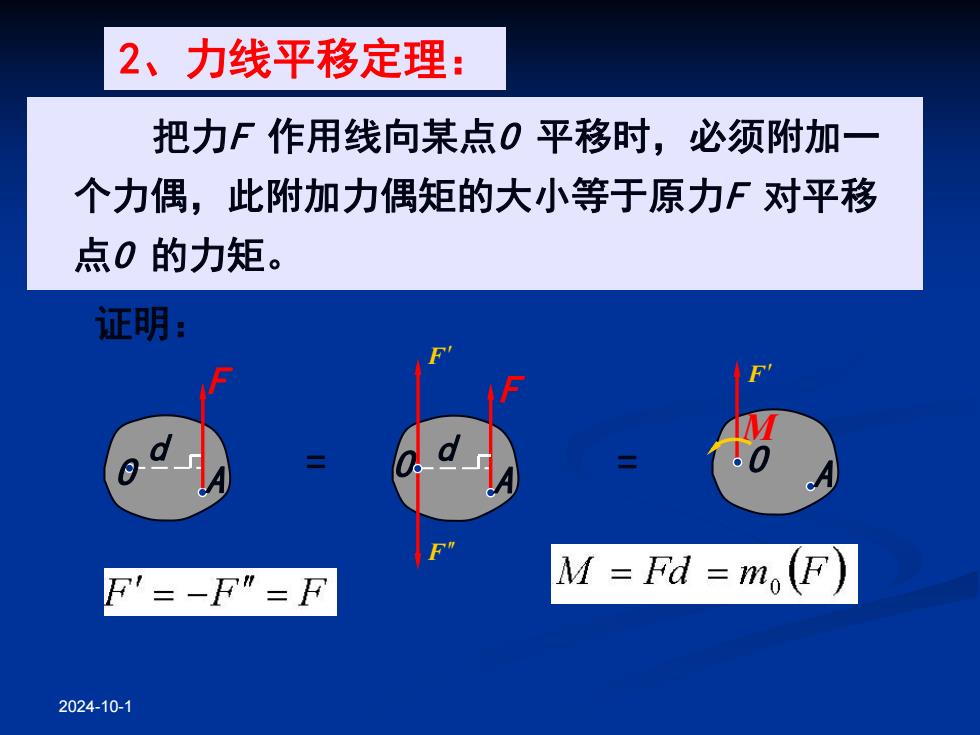
2024-10-1 F O A d F A O d F F M A O F = = 把力F 作用线向某点O 平移时,必须附加一 个力偶,此附加力偶矩的大小等于原力F 对平移 点O 的力矩。 证明: 2、力线平移定理:
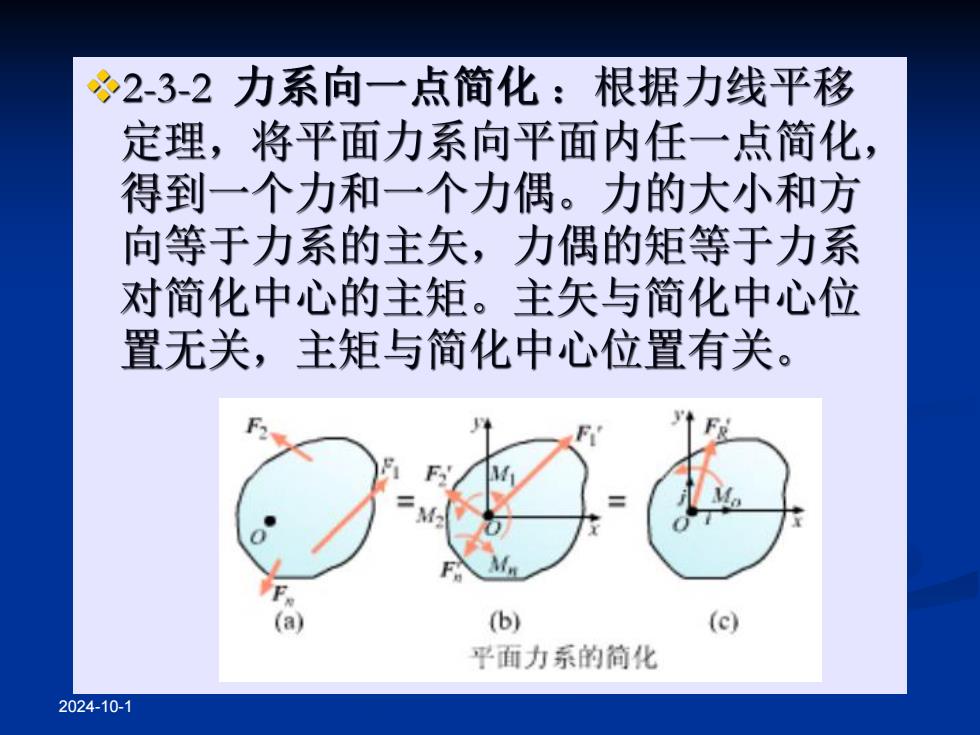
冬23-2力系向一点简化:根据力线平移 定理,将平面力系向平面内任一点简化, 得到一个力和一个力偶。力的大小和方 向等于力系的主矢,力偶的矩等于力系 对简化中心的主矩。主矢与简化中心位 置无关,主矩与简化中心位置有关。 (a) (b) (c) 平面力系的简化 2024-10-1
2024-10-1
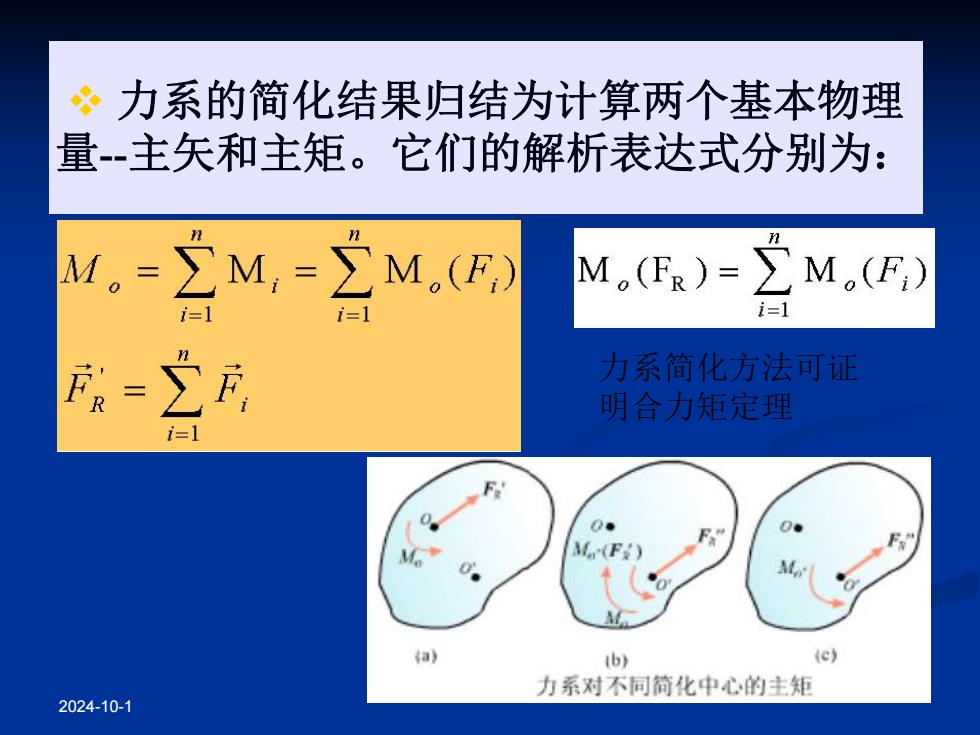
?力系的简化结果归结为计算两个基本物理 量-主矢和主矩。它们的解析表达式分别为: M。=∑M,=∑M,(E,) M,(FR)=∑M,(F) i=1 i=1 =】 力系简化方法可证 明合力矩定理 i=1 Q. M(F) a ib) (e) 力系对不同简化中心的主矩 2024-10-1
2024-10-1 v 力系的简化结果归结为计算两个基本物理 量-主矢和主矩。它们的解析表达式分别为: 力系简化方法可证 明合力矩定理
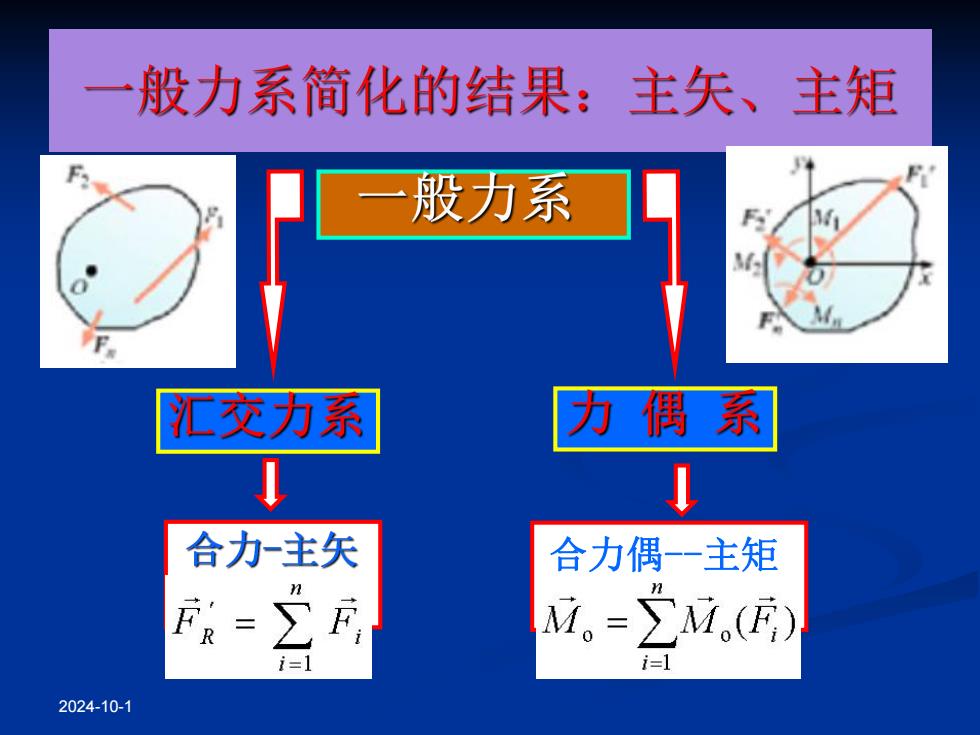
般力系简化的结果:主矢、主矩 一般力系 汇交力系 力偶系 合力-主矢 合力偶-主矩 1。=∑i,(瓦) i=1 i=1 2024-10-1
2024-10-1 合力偶-主矩 MO= MO ( Fi)
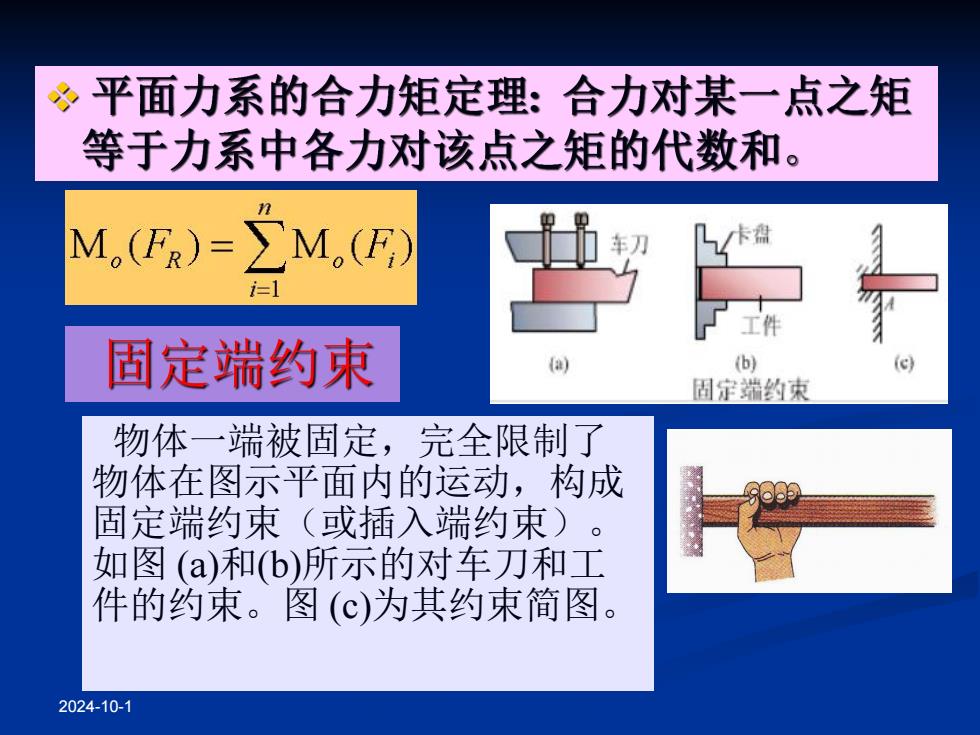
平面力系的合力矩定理:合力对某一点之矩 等于力系中各力对该点之矩的代数和。 M,(E)=∑M,(E) 卡盘 i= 工件 固定端约束 b 固定端约束 物体一端被固定,完全限制了 物体在图示平面内的运动,构成 固定端约束(或插入端约束)。 如图(a)和(b)所示的对车刀和工 件的约束。图(C)为其约束简图。 2024-10-1
2024-10-1 l物体一端被固定,完全限制了 物体在图示平面内的运动,构成 固定端约束(或插入端约束)。 如图 (a)和(b)所示的对车刀和工 件的约束。图 (c)为其约束简图

夕结论:平面力系圃定端约束的约束力包 括两个要直分力和一个约束力偶矩。 y FAy B 2024-10-1
2024-10-1 FAy FAx

力系的主矢 力系主矢的特点 > 对于给定的力系,主矢唯一; > 主矢仅与各力的大小和方向有关,主 矢不涉及作用点和作用线的具体位置,因 而主矢是自由矢。 2024-10-1
2024-10-1 Ø Ø

力系的主矩 力系主矩的特点 >力系主矩Mo与矩心(O)的位置有关 口力系主矩是定位矢量 2024-10-1
2024-10-1