工程力学教程第一卷 第于内学 解和安居,用被方秀分的贸点,O分别为正交与斜交坐标系。试将同一力F分别对再整标系进行分 解:(a),图(c):F=Fosai+Fsinah 分力:F1=Fos,F1=Fsina 投影:F=Fcosa,F=Fsina 讨论:P=90°时,投影与分力的模相等:分力是矢量,投影是代数量。 (b),图(d): 分力:Fa=(Fcsa-Fsinat),F2=FsnC方 极影:F。=Fsm Fy2=Fcos(o-a) 讨论:0≠90°时,投影与分量的模不等。 一2试画出图a、b两情形下各物体的受力图,并进行比较
— 1 — (a) (b) 习题 1-1 图 (a) (b) 习题 1-2 图 F FRD A C B D FAx FAy (a-1) FAy F A C B FAx ' FC (a-2) C D FC FRD (a-3) FAx FRD F A C B D FAy (b-1) 工程力学教程 第一卷 第一篇 工程静力学 第 1 章 引 论 1-1 图 a、b 所示,Ox1y1与 Ox2y2分别为正交与斜交坐标系。试将同一方 F 分别对两坐标系进行分 解和投影,并比较分力与力的投影。 解:(a),图(c): 1 1 F = F cos i + Fsin j 分力: 1 1 F F cos i x = , 1 1 F F sin j y = 投影: Fx1 = F cos , Fy1 = F sin 讨论: = 90°时,投影与分力的模相等;分力是矢量,投影是代数量。 (b),图(d): 分力: 2 2 F (F cos Fsin tan)i x = − , 2 2 sin sin F j F y = 投影: Fx2 = Fcos , cos( ) Fy2 = F − 讨论: ≠90°时,投影与分量的模不等。 1-2 试画出图 a、b 两情形下各物体的受力图,并进行比较。 1 Fy x 1 Fx 1 Fy 1 Fx y F (c) 2 Fx 2 Fy 2 y 2 x 2 Fx 2 Fy F (d)
比核L出课名香程圆两者之o值大小也不同
— 2 — 习题 1-3 图 比较:图(a-1)与图(b-1)不同,因两者之 FRD 值大小也不同。 1-3 试画出图示各物体的受力图。 F FAx FAy D C B A FB 或(a-2) F BFB FA D C A (a-1) FB FAx A FAy B F C (b-1) W FD B D C FAy FAx (c-1) F FA C B FB A 或(b-2) D FA A B C FB (d-1) FC C A FA (e-1) Ax F A Ay F D F D C B F 或(d-2) FB F C D B (e-2) Ox O F FOy W O1 F A (f-1) F FA DC A B FB (e-3) ' FA Ox O F FOy A W (f-2) FA O1 F A O1 (f-3) Fc FA FD FB FA FA
6、d所所西角赛德物并办作用在B牧上,杆出不计自质,杆D杆自重为以,试后出图 B 一5试用出图示结构中各杆的受力
— 3 — FAx C ' FCx ' FB B FAy ' FCy A (b-3) FE FD E D (a-3) FC F C E ' FE (a-2) 习题 1-4 图 习题 1-5 图 E FE B FB (b-2) FCx C FCy W T (b-1) FB B C ' FC D ' FD FAx FAy A (a-1) 1-4 图 a 所示为三角架结构。力 F1作用在 B 铰上。杆 AB 不计自重,杆 BD 杆自重为 W。试画出图 b、c、d 所示的隔离体的受力图,并加以讨论。 1-5 试画出图示结构中各杆的受力图。 B W FDy FDx D B2 F' F1 (d-2) FA A B B x2 F' B y2 F' F1 (c-1) FA A B B1 F (b-1) FDy F Dx D W B y2 F C B B x2 F (b-2) B x2 F' F1 B1 F' B y2 F' B (b-3) B W FDx D C B y2 F' B x2 F' (c-2) FA A B B1 F (d-1) FDy

习思1-6图 F沿其作 1一7试画出图示连续梁中的4C和CD架的受力图。 习题1一7图 1一8图示压路釅子可以在推力或拉力作用下滚过10Omm高的台阶.假定力F都是沿着连杆AB的方 向,与水平而成30°的夹角,碳子重为250N。试比较这两种情形下所需力F的大小。 解:图(a:0=acsm写 ΣF=0 Fsin(60°-Wsin8=0 500500 ∑F=0 Fcos(0-30)-W sin0=0 (a) F=217N 桌国于是中力已如.试分家其F工3所受的方。 5-5F拉 =(拉)
— 4 — 习题 1-8 图 FAy FAx ' FB ' FCC ' FD A D E FD FE ' FE E B FB FC C D (c) FA A D G F C FH H (a) FAx A FAy B FB C ' FCx ' FCy (a) F W 30 y x B FN (a) 30 x W FN F y (b) 1-6 图示刚性构件 ABC 由销钉 A 和拉杆 GH 支撑,在构件的点 C 作用有一水平力 F。试问如果将力 F 沿其作用线移至点 D 或点 E(如图示),是否会改变销钉 A 的受力状况。 解:由受力图 1-6a,1-6b 和 1-6c 分析可知,F 从 C 移至 E,A 端受力不变,这是因为力 F 在自身 刚体 ABC 上滑移;而 F 从 C 移至 D,则 A 端受力改变,因为 HG 与 ABC 为不同的刚体。 1-7 试画出图示连续梁中的 AC 和 CD 梁的受力图。 1-8 图示压路碾子可以在推力或拉力作用下滚过 100mm 高的台阶。假定力 F 都是沿着连杆 AB 的方 向,与水平面成 30°的夹角,碾子重为 250N。试比较这两种情形下所需力 F 的大小。 解:图(a): 5 4 = arcsin Fx = 0 F sin(60 − ) −W sin = 0 F = 1672 N 图(b): = 53.13 Fx = 0 F cos( − 30) −W sin = 0 F = 217N 1-9 两种正方形结构所受力 F 均已知。试分别求其中杆 1、2、3 所受的力。 解:图(a): 2F3 cos 45 − F = 0 F F 2 2 3 = (拉) F1 = F3(拉) 习题 1-6 图 习题 1-7 图 FA A F D C FH E H (b) FA A G F C FH FH D FG H H (c) FCx F1 FCy C F2 D FDy FDx (b)
F-25c0s45°=0 ”(受压 图(b:= 乃=F(受拉) 习1-9图 中产生的拔桩力(当a很小时,ama=a)。 2K=0.fmsa=f0Fa点al0r 习题1一10图 1一11图示起重机由周定塔AC与活动桁架BC组成。桁架BC用饺链连接于点C,并由钢索AB锥持 力Fc 习1-11图 解:图(a:ΣF=0,Fc0s号-W sino=0 F=2Wsm号 ∑F,=0,Fc-W-W cos-Fansin号=0 即F=W+cos+2Wsm2号 =W+Wcos+(1-coso)=2 -5
— 5 — 习题 1-11 图 FED D FDB F (a) FCB DB B F FAB (b) F2 − 2F3 cos45 = 0 F2 = F(受压) 图(b): F3 = F3 = 0 F1 = 0 ∴ F2 = F(受拉) 1-10 图示为一绳索拔桩装置。绳索的 E、C 两点拴在架子上,点 B 与拴在桩 A 上的绳索 AB 连接, 在点 D 加一铅垂向下的力 F,AB 可视为铅垂,DB 可视为水平。已知 = 0.1rad,力 F = 800N。试求绳 AB 中产生的拔桩力(当 很小时,tan ≈ )。 解: Fy = 0, FED sin = F sin F FED = Fx = 0, FED = FDB cos F F FDB 10 tan = = 由图(a)计算结果。 可推出图(b)中 FAB = 10FDB = 100F = 80 kN。 1-11 图示起重机由固定塔 AC 与活动桁架 BC 组成。桁架 BC 用铰链连接于点 C,并由钢索 AB 维持 其平衡。重 W = 40kN 的物体悬挂在钢索上,钢索绕过点 B 的滑轮,并沿直线 BC 引向铰盘。长度 AC = BC, 不计桁架重量和滑轮摩擦。试用角 =∠ACB 的函数来表示钢索 AB 的张力 FAB 以及桁架上沿直线 BC 的压 力 FBC 。 解:图(a): Fx = 0 , sin 0 2 cos − = FAB W ∴ 2 2 sin FAB = W Fy = 0, 0 2 − − cos − sin = FBC W W FAB 即 2 cos 2 sin2 FBC = W +W + W = W +W cos +W (1− cos) = 2W A F F3 F2 F1 (b-1) 习题 1-9 图 习题 1-10 图 F F3 45 F1 A 1 3 (a-1) F3 F2 D F3 (a-2) 3 D F F3 (b-2) FAB W FBC W x 2 y (a)
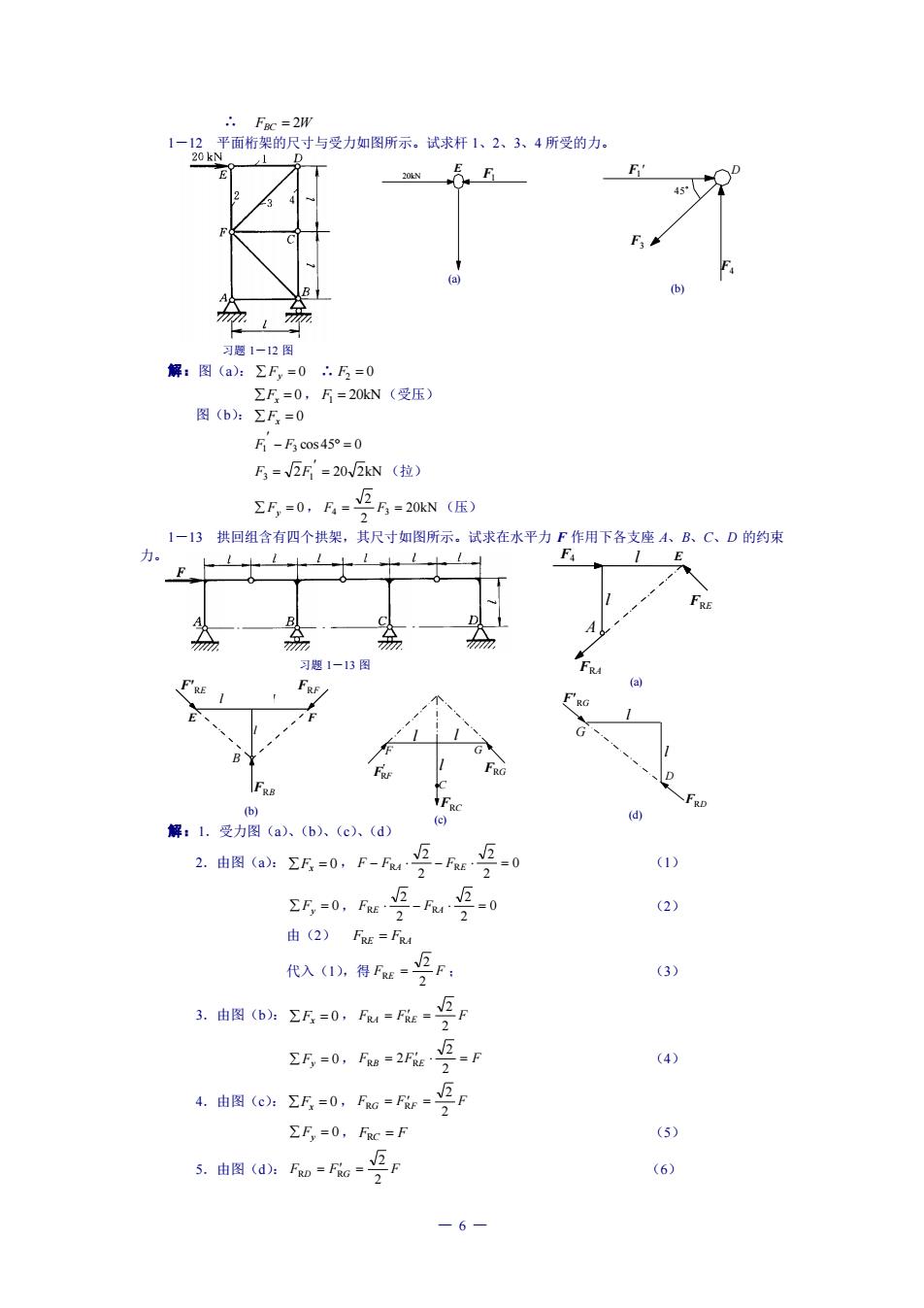
1一品平面指架的与受力如图所示。试求杆1、24所受的力: 解:图(a:ΣF,=05=0 图0 =20kN(受压 F-F COs45=0 =2R=202kN(拉) Σ,=0,E=2=20N(压) 1一13拱回组含有四个拱架,其尺寸如图所示。试求在水平力F作用下各支座小、B、C、D的约束 力。 习愿1-3图 C) 解:1.受力图(a.(b)、(c)、(d) 2.图a.E=0,F-5-E5=0 (1) -0,9-90 (2) 由(2)Fu=F 代入D得e一F (3) 由图=0,=:9 =0.=2e9=F (4) 4.由图(e:E=0,Fc=F=2F ∑F,=0,Fc=F (5) 5.由图dhR==F -6-
— 6 — F'RE FRF l l l B FRB E F (b) ' FRF FRG F l l l G C FRC (c) F'RG G l l D FRD (d) 习题 1-12 图 习题 1-13 图 F1 E 20kN (a) F4 E FRA A FRE l l (a) ∴ FBC = 2W 1-12 平面桁架的尺寸与受力如图所示。试求杆 1、2、3、4 所受的力。 解:图(a): Fy = 0 ∴ F2 = 0 Fx = 0, F1 = 20kN (受压) 图(b): Fx = 0 1 − 3 cos 45 = 0 F F 3 2 1 = 20 2kN F = F (拉) Fy = 0, 20kN 2 2 F4 = F3 = (压) 1-13 拱回组含有四个拱架,其尺寸如图所示。试求在水平力 F 作用下各支座 A、B、C、D 的约束 力。 解:1.受力图(a)、(b)、(c)、(d) 2.由图(a): Fx = 0 , 0 2 2 2 2 F − FRA − FRE = (1) Fy = 0, 0 2 2 2 2 FRE − FRA = (2) 由(2) FRE = FRA 代入(1),得 F E F 2 2 R = ; (3) 3.由图(b): Fx = 0 , F A F E F 2 2 R = R = Fy = 0, F B = F E = F 2 2 R 2 R (4) 4.由图(c): Fx = 0 , F G F F F 2 2 R = R = Fy = 0, FRC = F (5) 5.由图(d): F D F G F 2 2 R = R = (6) F3 F4 45 F1 D (b)
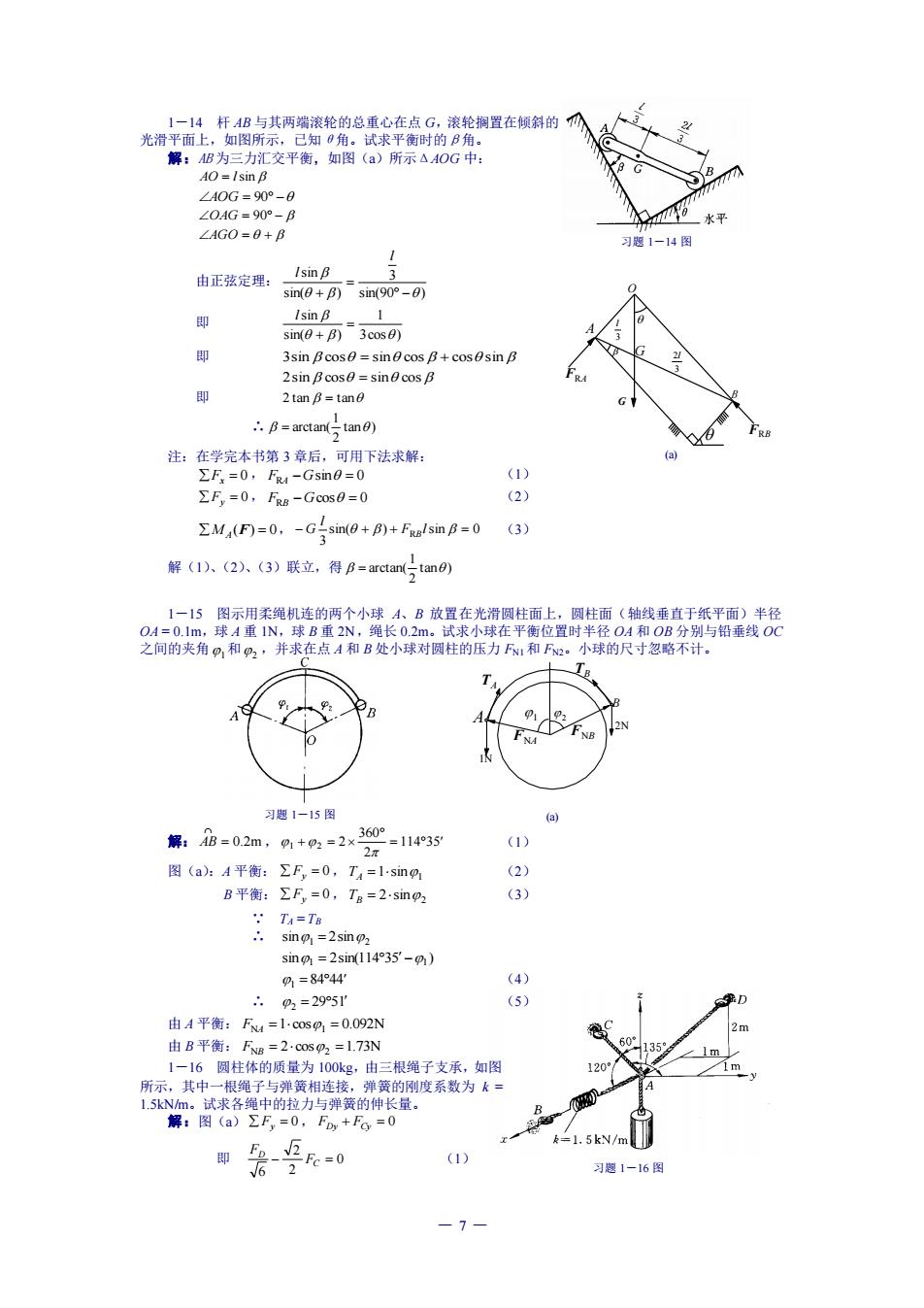
光滑平面,与其两端轮的总重心在点G,滚轮置在顿斜的网 解:B为三力汇交平葡,如图(a)所示△OG中: ∠04G-90-B ∠AG0=B+B Isin 8 由正弦定理: sin(0+B)sin(90-0) 即 Isin 6 sin(+B)3cos0) 即 3sin Bcos=sincosB+cossin B 2sin Boos0=sin0cosB 即 B=arctan(tano 注:在学完本书第3章后,可用下法求解。 5=0,f-Gsn0=0 ΣF,=0,FRs-Gcos0=0 (2 EM (F)=0,-Gsin(0+B)+Fualsin B=0 (3) 解(1).(2)、(3)联立,得B=arctan(tame) 1一15图示用柔绳机连的两个小球A、B放置在光滑圆柱面上,圆柱面《轴线垂直于纸平面)半径 习愿1-15图 解:B=02m,+2=2×360=1143 (2) 8平:2=0.7=2.sm (3) sin0=2snm1i4935-am) 2=84P44" (4) 0,=295r (5) 由A平衡:F4=1cosg,=0.092N 由B平衡:Fs=2.0o5O,=1.73N 1一16圆柱体的质量为100kg,由三根绳子支承,如图 所不、其中商相 即90 1.5kN/m (1) 习题1一16图
— 7 — 习题 1-14 图 习题 1-15 图 习题 1-16 图 TB B 2N TA A 1N FNA FNB 1 2 (a) 1-14 杆 AB 与其两端滚轮的总重心在点 G,滚轮搁置在倾斜的 光滑平面上,如图所示,已知θ角。试求平衡时的β角。 解:AB 为三力汇交平衡,如图(a)所示ΔAOG 中: AO = lsin AOG = 90 − OAG = 90 − AGO = + 由正弦定理: sin(90 ) 3 sin( ) sin − = + l l 即 3cos ) 1 sin( ) sin = + l 即 3sin cos = sin cos + cos sin 2sin cos = sin cos 即 2 tan = tan ∴ tan ) 2 1 = arctan( 注:在学完本书第 3 章后,可用下法求解: Fx = 0, FRA −Gsin = 0 (1) Fy = 0, FRB −Gcos = 0 (2) MA (F) = 0, sin( ) sin 0 3 − + + FR l = l G B (3) 解(1)、(2)、(3)联立,得 tan ) 2 1 = arctan( 1-15 图示用柔绳机连的两个小球 A、B 放置在光滑圆柱面上,圆柱面(轴线垂直于纸平面)半径 OA = 0.1m,球 A 重 1N,球 B 重 2N,绳长 0.2m。试求小球在平衡位置时半径 OA 和 OB 分别与铅垂线 OC 之间的夹角 1 和 2 ,并求在点 A 和 B 处小球对圆柱的压力 FN1和 FN2。小球的尺寸忽略不计。 解: = 0.2m AB , = + = 114 35 2 360 1 2 2 (1) 图(a):A 平衡: Fy = 0, 1 TA =1sin (2) B 平衡: Fy = 0, 2 TB = 2sin (3) ∵ TA = TB ∴ 1 2 sin = 2sin sin 2sin(114 35 ) 1 −1 = 1 = 8444 (4) ∴ 2 = 2951 (5) 由 A 平衡: FNA =1 cos1 = 0.092N 由 B 平衡: FNB = 2 cos2 =1.73N 1-16 圆柱体的质量为 100kg,由三根绳子支承,如图 所示,其中一根绳子与弹簧相连接,弹簧的刚度系数为 k = 1.5kN/m。试求各绳中的拉力与弹簧的伸长量。 解:图(a) Fy = 0, FDy + FCy = 0 即 0 2 2 6 − C = D F F (1) A 3 l G G B FRB FRA 3 2l O (a)

F:=0.F8+F+Fom=0 即-店=0 (2) ΣF=0,-R+Fc+Fs=0 -mg+F+2F=0 (3) 解D2(3)联立, (F -51N E-887N Fa=618N 品+ 习题1-17图 显然T=理 25=0,e-1i2fms260=0 即F-T-F4=0 (3) Σ5=0.-55-25,5-w-5-040 解; ΣF=0,F=F F=0,F=2F sin15 (2) 2.节点0,受力图(b: F=0,Fac=Fe (3) Σk=0,9ha-F (4) 5,=0,号+2c=0 (5) Fac=-0.366F(压
— 8 — 习题 1-18 图 z D FC FB FD y x A 120 60 135 mg (a) Fx = 0 , FB + FCx + FDx = 0 即 0 6 1 2 1 FB − FC − FD = (2) Fz = 0, −mg + FCz + FDz = 0 即 0 6 2 2 1 − mg + FC + FD = (3) 解(1)、(2)、(3)联立,得 = = = 618N 887N 512N B D C F F F ∴ 0.412m 1500 618 st = = = k FB 1-17 由三脚架 ABCD、铰车 E 和滑轮 D 组成的提升机构,从矿井中吊重 W = 30 kN 的物体,如图 所示。若图中 ABC 为等边三角形,各杆和绳索 DE 与水平面都成 60°角。试求当物体被匀速起吊时各杆所 受的力。 解:节点 D,受力图(a): Fx = 0,FA = FB (1) 显然 TE = W (2) Fy = 0, 2 cos 60 0 2 1 2 1 2 FC − TE − FA = 即 FC −TE − FA = 0 (3) Fz = 0, 0 2 3 2 3 2 2 3 − FC − FA −W −TE = (4) 解(1)、(2)、(3)、(4)联立,得 FC = -1.55kN(受压) FA = -31.5kN(受压) FB = -31.5kN(受压) 1-18 图示为高压输电线路铁塔的绝缘磁性的悬挂部分。电线悬挂于铅垂面内,其拉力 FT 与水平线 夹角为 15°。FT 的大小为已知。试求塔架中 AO、BO、CO 三杆所受的力。 解:1.节点 E,受力图(a): Fx = 0, FT FT = (1) Fy = 0, F = 2FT sin15° (2) 2.节点 O,受力图(b): Fx = 0, FOC = FOB (3) Fz = 0, FOA = F 2 2 (4) Fy = 0, 0 2 2 2 2 2 FOA + FOC = (5) 解以上联立,得 FOA = 0.732FT(拉) FOC = -0.366FT(压) 习题 1-17 图 TE 60 z D FC FA W B FB 60 y A x E 60 60 60 C (a)
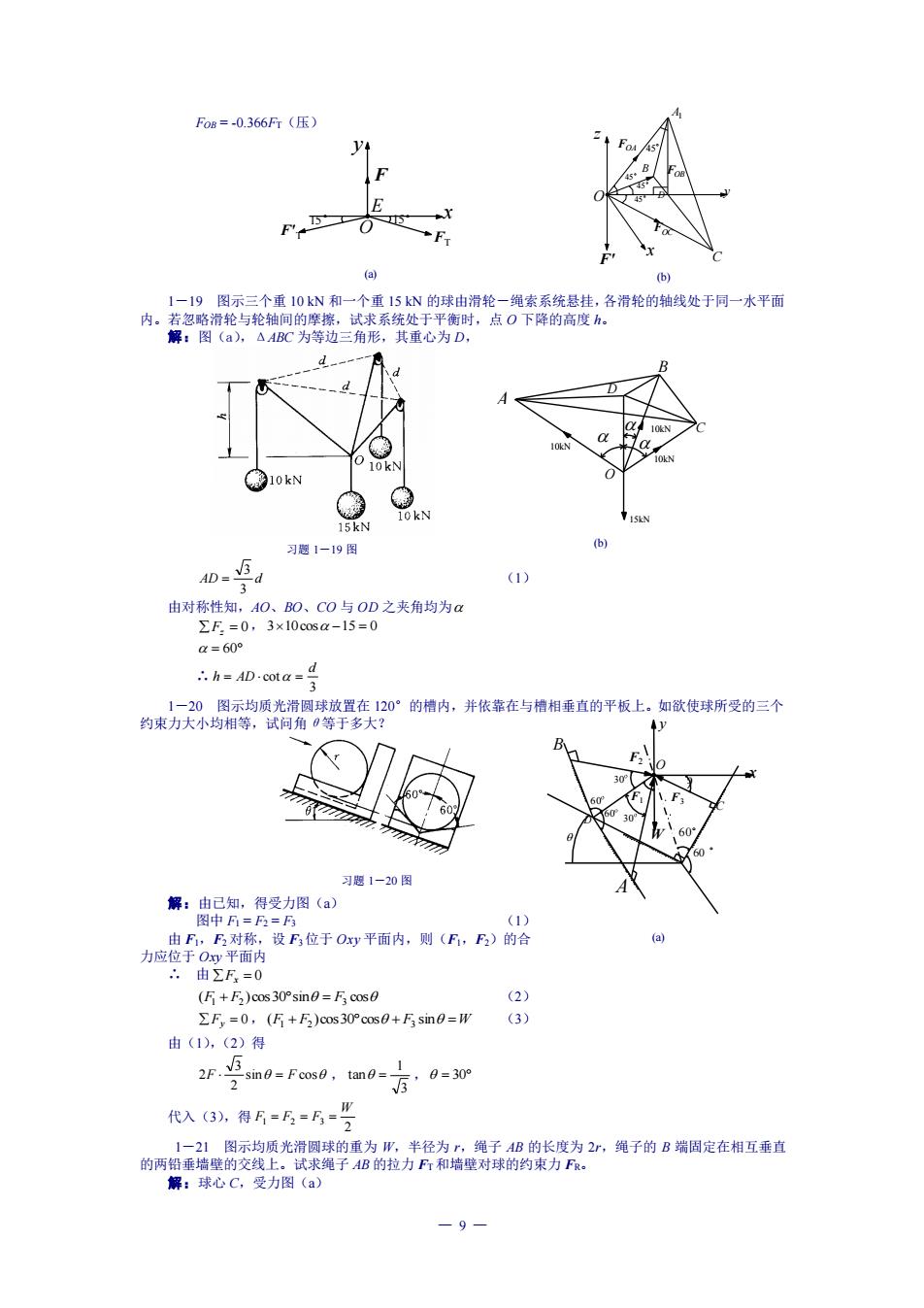
F0B=-0.366F(压) 1一19图示三个重10kN和一个重15N的球由滑轮一绳索系统悬挂,各滑轮的轴线处于同一水平面 解:图为等边三角泰统为时。点0下降的商度 习题1-19图 AD=d (1】 a=60 六h=AD-cota= 束天失头0的情内并事在与相重直的平板上,欧使球所受 三个 习1一20图 点”成手o的则月哈 ΣF=0,(5+5)oms30°cos0+5sm0=w 由(1),(2)得 代入(3,得=5=5=号 丽品品热金品在 -9
— 9 — x B A 30 60 60 30 60 60 F2 F1 W F3 D C O y (a) FOB = -0.366FT(压) 1-19 图示三个重 10 kN 和一个重 15 kN 的球由滑轮-绳索系统悬挂,各滑轮的轴线处于同一水平面 内。若忽略滑轮与轮轴间的摩擦,试求系统处于平衡时,点 O 下降的高度 h。 解:图(a),ΔABC 为等边三角形,其重心为 D, AD d 3 3 = (1) 由对称性知,AO、BO、CO 与 OD 之夹角均为 Fz = 0, 310cos −15 = 0 = 60 ∴ 3 cot d h = AD = 1-20 图示均质光滑圆球放置在 120°的槽内,并依靠在与槽相垂直的平板上。如欲使球所受的三个 约束力大小均相等,试问角θ等于多大? 解:由已知,得受力图(a) 图中 F1 = F2 = F3 (1) 由 F1,F2 对称,设 F3位于 Oxy 平面内,则(F1,F2)的合 力应位于 Oxy 平面内 ∴ 由 Fx = 0 (F1 + F2 )cos30sin = F3 cos (2) Fy = 0, (F1 + F2 )cos30cos + F3 sin =W (3) 由(1),(2)得 sin cos 2 3 2F = F , 3 1 tan = , = 30 代入(3),得 2 1 2 3 W F = F = F = 1-21 图示均质光滑圆球的重为 W,半径为 r,绳子 AB 的长度为 2r,绳子的 B 端固定在相互垂直 的两铅垂墙壁的交线上。试求绳子 AB 的拉力 FT 和墙壁对球的约束力 FR。 解:球心 C,受力图(a) z A1 y C FOA 45 FOB B 45 D F' x FOC O 45 45 (b) 习题 1-19 图 习题 1-20 图 F'T y F FT 15 15 E O x (a) C A B 10kN O 15kN D 10kN 10kN (b)
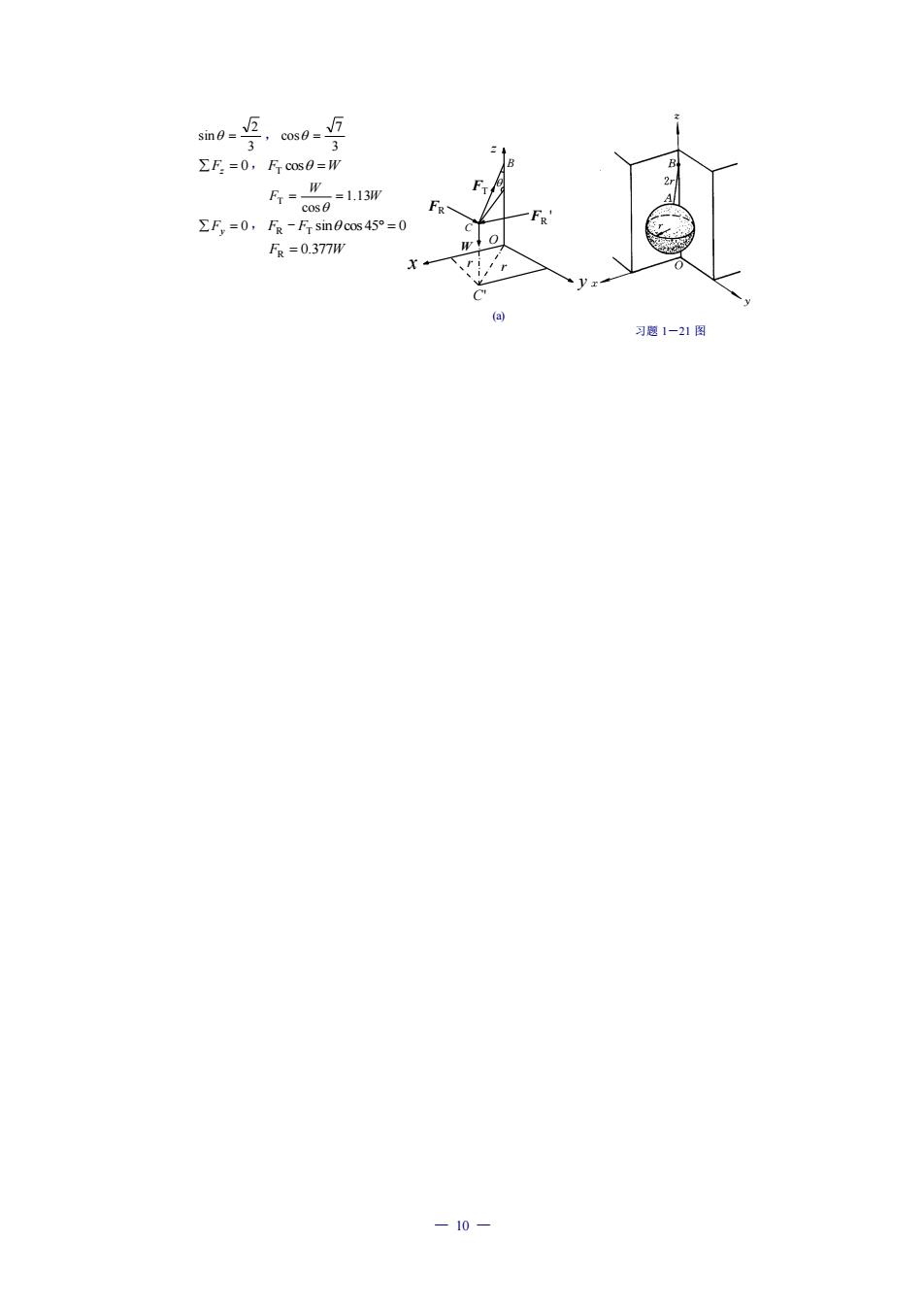
m0=5,s0=5 ∑E=0,Fc0s0=W -1.13训 F,=0, 0cos450= -0377W 习愿1-21图 -10
— 10 — 习题 1-21 图 z FR FT ' FR CW O y x B C' r r (a) 3 2 sin = , 3 7 cos = Fz = 0, FT cos =W W W F 1.13 cos T = = Fy = 0, FR - FT sin cos 45 = 0 FR = 0.377W