
海南大学《工程力学(1)》试卷 2006年1月 海南大学理工学院 2004土木工程(本科)专业《工程力学(I)》试题(B卷) (答案) 考试说明:本课程为闭卷考试,可携带水笔、圆珠笔、铅笔、直尺、橡皮和无编程功 能的计算器, 得分 阅卷教师 一、单项选择题(每题4分,共20分,在括 号内填写所选答案前的字母) (A)1.平面汇交力系合力不为零,向平面内汇交点以外一点简化, 其结果: (A)可能是一个力,也可能是一个力和一个力偶。 (B)只可能是一个力。 (C)只可能是一个力偶。 D)只可能是一个力和一个力偶。 (C)2.如图所示平面桁架处于平衡,其中内力为零的构件的根数是: (A)5根。 (B) 6根 (C) 7根。 (D) 8根
海南大学《工程力学(I)》试卷 2006 年 1 月 1 海南大学 理工 学院 2004 土木工程(本科)专业《工程力学(I)》试题(B 卷) (答案) 考试说明:本课程为闭卷考试,可携带 水笔、圆珠笔、铅笔、直尺、橡皮和无编程功 能的计算器 。 一、单项选择题(每题 4 分,共 20 分,在括 号内填写所选答案前的字母) ( A ) 1.平面汇交力系合力不为零,向平面内汇交点以外一点简化, 其结果: (A) 可能是一个力,也可能是一个力和一个力偶。 (B) 只可能是一个力。 (C) 只可能是一个力偶。 (D) 只可能是一个力和一个力偶。 ( C ) 2. 如图所示平面桁架处于平衡,其中内力为零的构件的根数是: (A) 5 根。 (B) 6 根。 (C) 7 根。 (D) 8 根。 得分 阅卷教师 F3 F1 F4 F2

海南大学《工程力学()》试卷 2006年1月 (A)3.如图所示,F、F(方向如图,大小为正)分别作用于刚体 上A、B两点,且F、F与刚体上另一点C点共面,则下述说法正确的是: F (A)在A点加一个适当的力可以使系统平衡。 (B)在B点加一个适当的力可以使系统平衡。 (C)在C点加一个适当的力可以使系统平衡。 (D)在系统上加一个适当的力偶可以使系统平衡。 (A)4.关于低碳钢的力学性能,下述说法中正确的是: (A)低碳钢在拉伸试验中,其变形可分为弹性阶段、屈服阶段、强化阶段 和局部变形阶段。 (B)在屈服阶段,应力波动不大,通常将上屈服强度称为材料的屈服极限。 (C)在强化阶段,通过冷作硬化可以提高材料的比例极限和塑性变形能力。 (D)低碳钢属于塑性材料,所以只可能发生塑性屈服破坏。 (C)5.材料力学中,弹性模量E与横截面对中性轴的惯性矩L的乘 积EL表示杆件的: (A)拉伸(压缩)刚度。 (B)扭转刚度。 (C)弯曲刚度。 D)弯曲截面系数 得分 阅卷教师 二、填空题(每空3分,共24分)
海南大学《工程力学(I)》试卷 2006 年 1 月 2 ( A ) 3. 如图所示,F1、F2(方向如图,大小为正)分别作用于刚体 上 A、B 两点,且 F1、F2 与刚体上另一点 C 点共面,则下述说法正确的是: (A) 在 A 点加一个适当的力可以使系统平衡。 (B) 在 B 点加一个适当的力可以使系统平衡。 (C) 在 C 点加一个适当的力可以使系统平衡。 (D) 在系统上加一个适当的力偶可以使系统平衡。 ( A ) 4. 关于低碳钢的力学性能,下述说法中正确的是: (A) 低碳钢在拉伸试验中,其变形可分为弹性阶段、屈服阶段、强化阶段 和局部变形阶段。 (B) 在屈服阶段,应力波动不大,通常将上屈服强度称为材料的屈服极限。 (C) 在强化阶段,通过冷作硬化可以提高材料的比例极限和塑性变形能力。 (D) 低碳钢属于塑性材料,所以只可能发生塑性屈服破坏。 ( C ) 5. 材料力学中,弹性模量 E 与横截面对中性轴的惯性矩 Iz 的乘 积 EIz 表示杆件的: (A) 拉伸(压缩)刚度。 (B) 扭转刚度。 (C) 弯曲刚度。 (D) 弯曲截面系数。 二、填空题(每空 3 分,共 24 分) F1 F1 F2 A B C 得分 阅卷教师
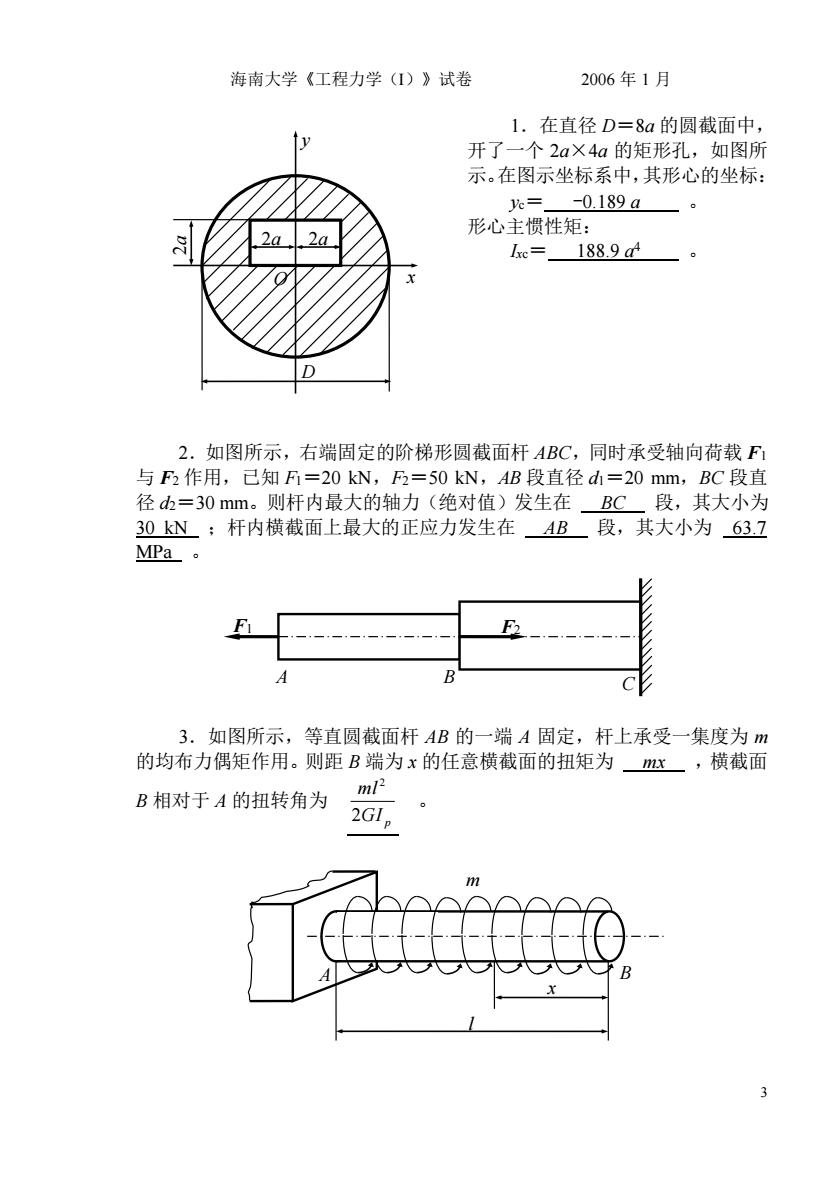
海南大学《工程力学(1)》试卷 2006年1月 1.在直径D=8a的圆截面中, 开了一个2a×4a的矩形孔,如图所 示。在图示坐标系中,其形心的坐标: k=-0.189a 形心主惯性矩: 1e=188.9d 2.如图所示,右端固定的阶梯形圆截面杆ABC,同时承受轴向荷载F 与F2作用,己知F=20kN,F2=50kN,AB段直径d=20mm,BC段直 径d=30mm。则杆内最大的轴力(绝对值)发生在BC段,其大小为 30kN:杆内横截面上最大的正应力发生在AB段,其大小为63.2 MPa· B 3.如图所示,等直圆截面杆AB的一端A固定,杆上承受一集度为m 的均布力偶矩作用。则距B端为x的任意横截面的扭矩为mx,横截面 B相对于A的扭转角为 ml2 2G1
海南大学《工程力学(I)》试卷 2006 年 1 月 3 1.在直径 D=8a 的圆截面中, 开了一个 2a×4a 的矩形孔,如图所 示。在图示坐标系中,其形心的坐标: yc= -0.189 a 。 形心主惯性矩: Ixc= 188.9 a 4 。 2.如图所示,右端固定的阶梯形圆截面杆 ABC,同时承受轴向荷载 F1 与 F2 作用,已知 F1=20 kN,F2=50 kN,AB 段直径 d1=20 mm,BC 段直 径 d2=30 mm。则杆内最大的轴力(绝对值)发生在 BC 段,其大小为 30 kN ;杆内横截面上最大的正应力发生在 AB 段,其大小为 63.7 MPa 。 3.如图所示,等直圆截面杆 AB 的一端 A 固定,杆上承受一集度为 m 的均布力偶矩作用。则距 B 端为 x 的任意横截面的扭矩为 mx ,横截面 B 相对于 A 的扭转角为 GI p ml 2 2 。 m x l A B F2 F1 F1 F1 A B C x y O 2a 2a 2 a D
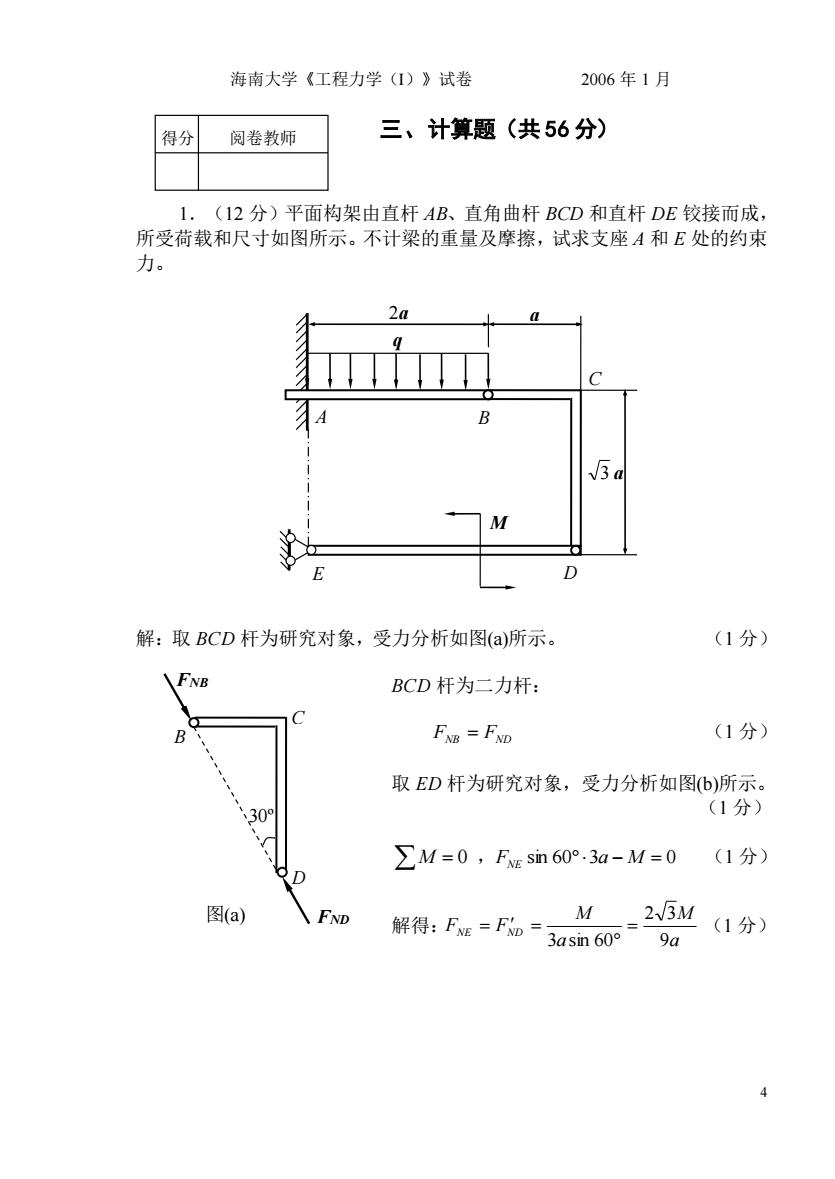
海南大学《工程力学()》试卷 2006年1月 得分 阅卷教师 三、计算题(共56分) 1.(12分)平面构架由直杆AB、直角曲杆BCD和直杆DE较接而成, 所受荷载和尺寸如图所示。不计梁的重量及摩擦,试求支座A和E处的约束 力。 2a B 3a M E 解:取BCD杆为研究对象,受力分析如图(a)所示。 (1分) FNB BCD杆为二力杆: FNB=FND (1分) 取ED杆为研究对象,受力分析如图b)所示。 30 (1分) ∑M=0,Fsn60°.3a-M=0(1分) 图(a) FND M25M(1分) 解得:Fe=Fn=3asn60° 9a
海南大学《工程力学(I)》试卷 2006 年 1 月 4 三、计算题(共 56 分) 1.(12 分)平面构架由直杆 AB、直角曲杆 BCD 和直杆 DE 铰接而成, 所受荷载和尺寸如图所示。不计梁的重量及摩擦,试求支座 A 和 E 处的约束 力。 解:取 BCD 杆为研究对象,受力分析如图(a)所示。 (1 分) BCD 杆为二力杆: FNB = FND (1 分) 取 ED 杆为研究对象,受力分析如图(b)所示。 (1 分) M = 0 ,FNE sin 60 3a − M = 0 (1 分) 解得: a M a M FNE FND 9 2 3 3 sin 60 = = = (1 分) M q A C B E D 2a a 3 a 得分 阅卷教师 B C D FND FNB 图(a) 30º
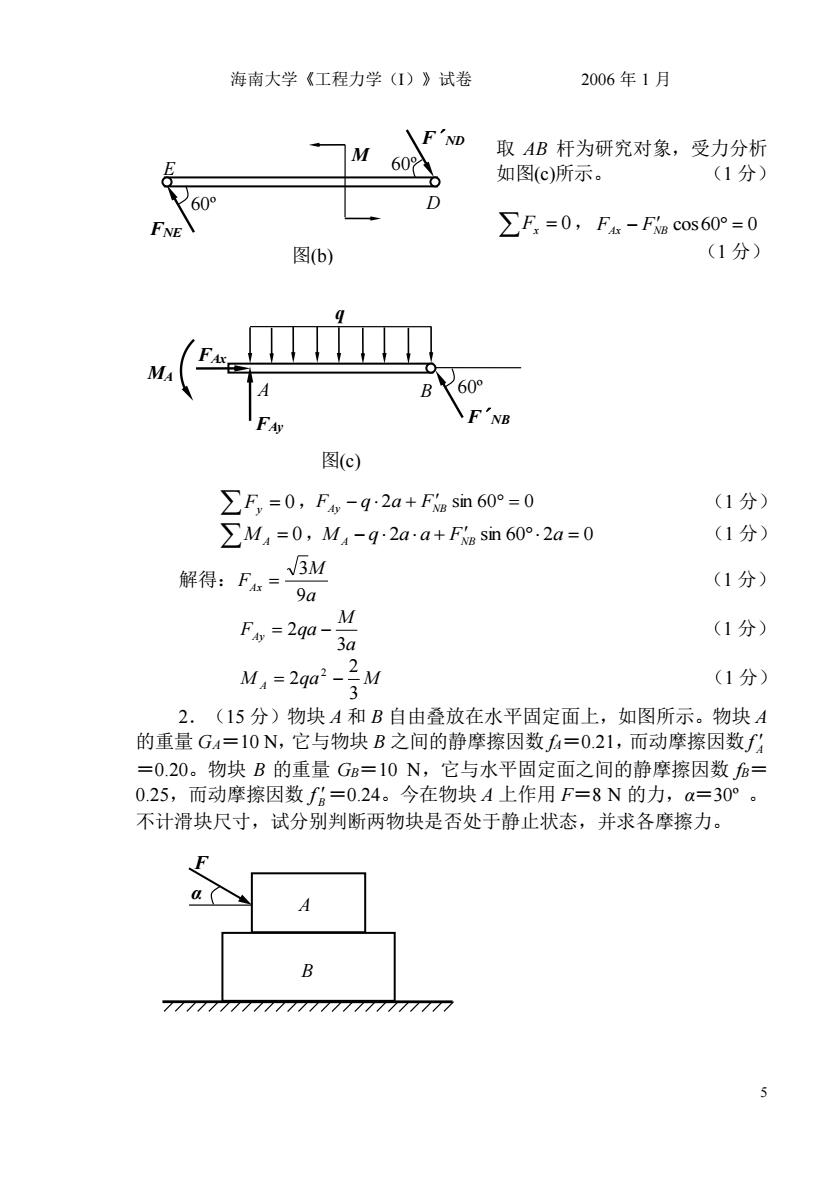
海南大学《工程力学(1)》试卷 2006年1月 AF ND M60 取AB杆为研究对象,受力分析 如图(c)所示。 (1分 60 ∑F=0,F-Fcos60°=0 图(b) (1分) u( B 60° F F'NB 图(c) ∑F,=0,F,-q2a+Fke Sin60°=0 (1分)》 ∑M,=0,M4-g-2aa+Fsin60°.2a=0 (1分 :-受 (1分) Fv=2qd-3a M (1分) M=2g如2-号M (1分) 2.(15分)物块A和B自由叠放在水平固定面上,如图所示。物块A 的重量G4=10N,它与物块B之间的静摩擦因数fA=0.21,而动摩擦因数f升 =0.20。物块B的重量GB=10N,它与水平固定面之间的静摩擦因数B= 0.25,而动摩擦因数∫6=0.24。今在物块A上作用F=8N的力,a=30°。 不计滑块尺寸,试分别判断两物块是否处于静止状态,并求各摩擦力。 a 777777777777777777777 5
海南大学《工程力学(I)》试卷 2006 年 1 月 5 取 AB 杆为研究对象,受力分析 如图(c)所示。 (1 分) Fx = 0, FAx − FNB cos60 = 0 (1 分) Fy = 0,FAy − q 2a + FNB sin 60 = 0 (1 分) M A = 0,M A − q 2a a + FNB sin 60 2a = 0 (1 分) 解得: a M FAx 9 3 = (1 分) a M FAy qa 3 = 2 − (1 分) M A qa M 3 2 2 2 = − (1 分) 2.(15 分)物块 A 和 B 自由叠放在水平固定面上,如图所示。物块 A 的重量 GA=10 N,它与物块 B 之间的静摩擦因数 fA=0.21,而动摩擦因数 A f =0.20。物块 B 的重量 GB=10 N,它与水平固定面之间的静摩擦因数 fB= 0.25,而动摩擦因数 B f =0.24。今在物块 A 上作用 F=8 N 的力,α=30º。 不计滑块尺寸,试分别判断两物块是否处于静止状态,并求各摩擦力。 F A B α q A B F F´NB Ay FAx MA 60º 图(c) M F´ND FNE 60º 60º 图(b) D E

海南大学《工程力学(I)》试卷 2006年1月 解:取物块A为研究对象,受力分析如图(a)所示 (1分) GA ∑F=0,Fcosa-F4=0 (1分) ∑F=0,-Fsna+F4-G4=0(1分) 解得: F=6.93N (1分) F4=14W (1分) 物块A与B之间最大静滑动摩擦力: 图(a) F4mx=f4F4=0.21×14=2.94N (1分) F>Fm,物块A相对于物块B滑动。 (1分) 物块A与B之间的动滑动摩擦力: F=fF4=0.20×14=2.8N(水平向左) (1分) 取物块B为研究对象,受力分析如图b)所示。 (1分) ∑F=0,F-F=0 (1分) F"A ∑E=0,-FM+FB-GB=0 (1分) B 解得:Fa=2.8N (1分) FNB =34N (1分) 物块B与水平固定面之间最大静滑动摩擦 FNB 力: 图b) Fa,m=faFs=0.25×34=8.5N (1分) Fa<Fa.mx,物块B处于静止,F。=2.8N(水平向左) (1分) 3.(9分)作图示外伸梁的剪力图和弯矩图,并指出剪力和弯矩的极 值
海南大学《工程力学(I)》试卷 2006 年 1 月 6 解:取物块 A 为研究对象,受力分析如图(a)所示。 (1 分) Fx = 0,F cos − FA = 0 (1 分) Fy = 0,− F sin + FNA − GA = 0 (1 分) 解得: FA = 6.93N (1 分) FNA =14N (1 分) 物块 A 与 B 之间最大静滑动摩擦力: FA,max = f AFNA = 0.2114 = 2.94N (1 分) FA FA,max ,物块 A 相对于物块 B 滑动。 (1 分) 物块 A 与 B 之间的动滑动摩擦力: FA = fA FNA = 0.2014 = 2.8N (水平向左) (1 分) 取物块 B 为研究对象,受力分析如图(b)所示。 (1 分) Fx = 0,FA − FB = 0 (1 分) Fy = 0,− FNA + FNB − GB = 0 (1 分) 解得: FB = 2.8N (1 分) FNB = 34N (1 分) 物块 B 与水平固定面之间最大静滑动摩擦 力: FB,max = fBFNB = 0.2534 = 8.5N (1 分) FB FB,max ,物块 B 处于静止, FB = 2.8N (水平向左) (1 分) 3.(9 分)作图示外伸梁的剪力图和弯矩图,并指出剪力和弯矩的极 值。 F A α GA FNA FA 图(a) B F′′A FNB GB F′NA 图(b) FB F1
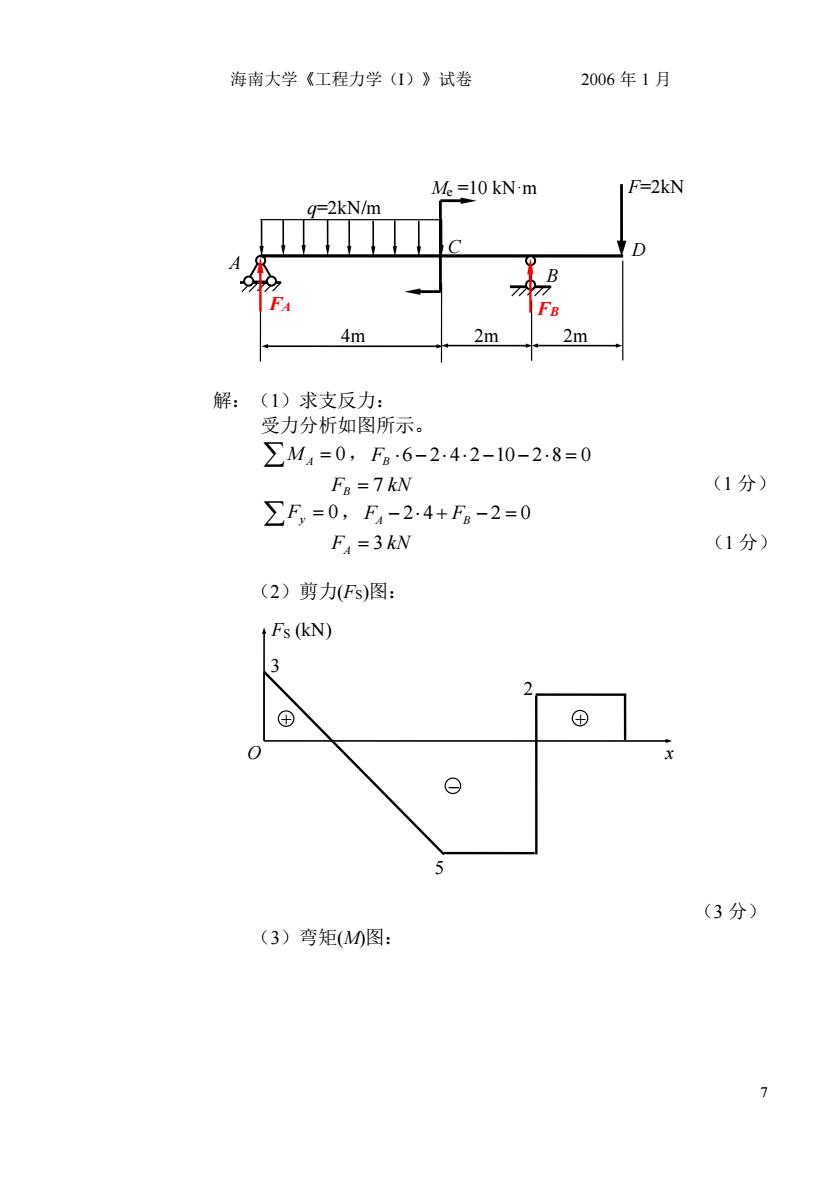
海南大学《工程力学(1)》试卷 2006年1月 Me=10 kN.m F=2kN g=2kN/m 0 4 % 4m 2m 2m 解:(1)求支反力: 受力分析如图所示。 ∑M4=0,Fg6-2.42-10-28=0 Fg=7kN (1分) ∑F=0,F4-24+F。-2=0 F=3kN (1分) (2)剪力Fs)图: Fs (kN) 3 (3分) (3)弯矩(0图: 1
海南大学《工程力学(I)》试卷 2006 年 1 月 7 解:(1)求支反力: 受力分析如图所示。 M A = 0, FB 6 − 2 4 2 −10 − 28 = 0 FB = 7 kN (1 分) Fy = 0, FA − 2 4 + FB − 2 = 0 FA = 3 kN (1 分) (2)剪力(FS)图: (3 分) (3)弯矩(M)图: Me =10 kN·m q=2kN/m A C B 4m FA FB F=2kN D 2m 2m 3 FS (kN) O x _ + 5 2 +
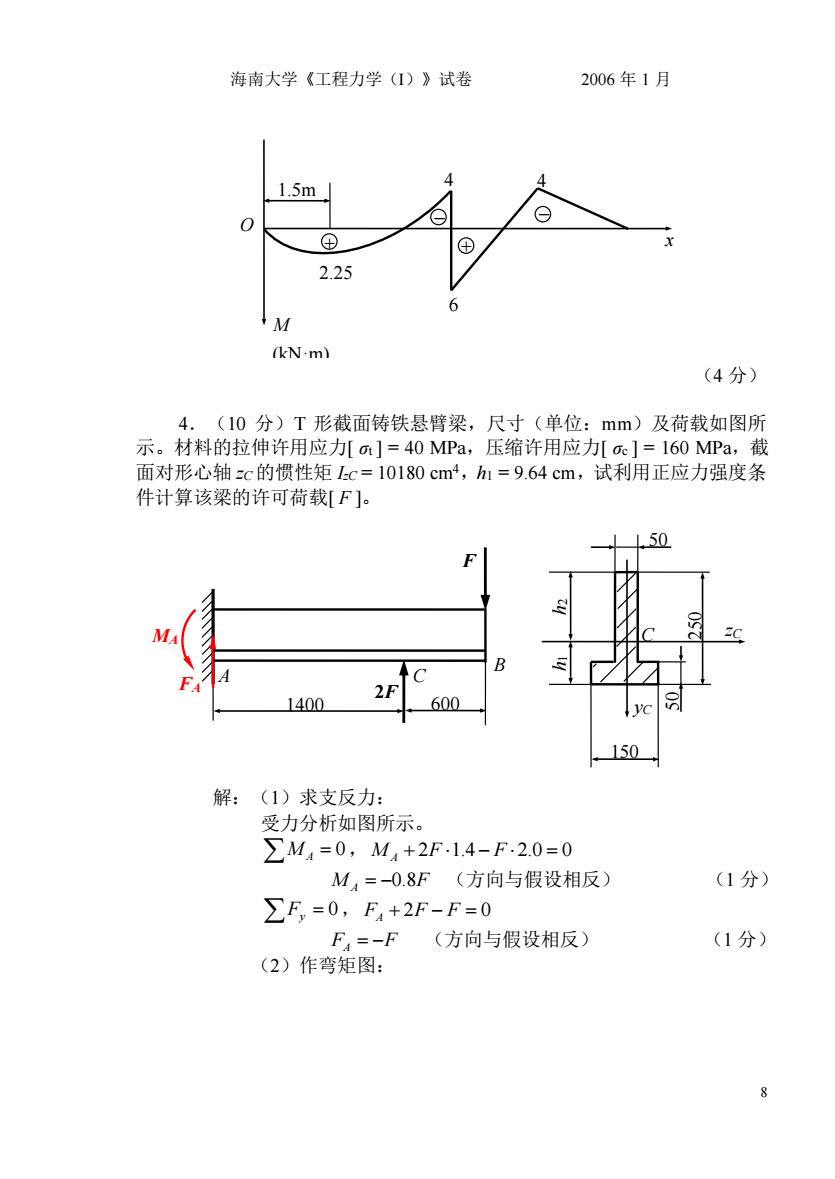
海南大学《工程力学()》试卷 2006年1月 1.5m 2.25 (kN.m) (4分) 4.(10分)T形截面铸铁悬臂梁,尺寸(单位:mm)及荷载如图所 示。材料的拉伸许用应[m]=40MPa,压缩许用应[c]=l60MPa,截 面对形心轴zc的惯性矩1c=10180cm4,h1=9.64cm,试利用正应力强度条 件计算该梁的许可荷载[F]。 50 2F 1400 600 150 解:(1)求支反力: 受力分析如图所示。 ∑M4=0,M4+2F.14-F.2.0=0 M,=-0.8F(方向与假设相反) (1分) ∑F,=0,F4+2F-F=0 F4=-F (方向与假设相反) (1分) (2)作弯矩图:
海南大学《工程力学(I)》试卷 2006 年 1 月 8 (4 分) 4.(10 分)T 形截面铸铁悬臂梁,尺寸(单位:mm)及荷载如图所 示。材料的拉伸许用应力[ σt ] = 40 MPa,压缩许用应力[ σc ] = 160 MPa,截 面对形心轴 zC的惯性矩 IzC = 10180 cm4,h1 = 9.64 cm,试利用正应力强度条 件计算该梁的许可荷载[ F ]。 解:(1)求支反力: 受力分析如图所示。 M A = 0, MA + 2F 1.4 − F 2.0 = 0 M A = −0.8F (方向与假设相反) (1 分) Fy = 0, FA + 2F − F = 0 FA = −F (方向与假设相反) (1 分) (2)作弯矩图: M (kN·m) O + x + _ _ 1.5m 2.25 4 4 6 A MA F 1400 600 B F B F1 2F FA C yC zC 150 250 50 h1 h2 50 C F B F1

海南大学《工程力学(1)》试卷 2006年1月 0.6F O 08r (1分) M=0.8F,Mc=-0.6F (1分) (3)求[F] 由强度条件:-M=≤问 (1分) A截面:由拉伸强度要求得 s,[a]=。8×40x10x1o180x10 =52.8kW (1分) 0.8h 9.64×10- 由压缩强度要求得 =132.6kN(1分) h 15.36×10- C截面:由拉伸强度要求得 F ↓×g,L=1×40x10x10180x10 =44.2kN 0.60.6 15.36×10- (1分) 由压缩强度要求得 F≤↓×g1L=1×160x10×10180×10- 0.6h0.6 =281.6kN(1分) 9.64×10- 综合上述结果,许可荷载[F]=44.2kN。 (1分)
海南大学《工程力学(I)》试卷 2006 年 1 月 9 (1 分) M A = 0.8F ,MC = −0.6F (1 分) (3)求[ F ] 由强度条件: [ ] max max max = zC I M y (1 分) A 截面:由拉伸强度要求得 k N h I F t zc 52.8 9.64 10 40 10 10180 10 0.8 [ ] 1 0.8 1 2 6 8 1 = = − − (1 分) 由压缩强度要求得 k N h I F c z c 132.6 15.36 10 160 10 10180 10 0.8 [ ] 1 0.8 1 2 6 8 2 = = − − (1 分) C 截面:由拉伸强度要求得 k N h I F t zc 44.2 15.36 10 40 10 10180 10 0.6 [ ] 1 0.6 1 2 6 8 2 = = − − (1 分) 由压缩强度要求得 k N h I F c z c 281.6 9.64 10 160 10 10180 10 0.6 [ ] 1 0.6 1 2 6 8 1 = = − − (1 分) 综合上述结果,许可荷载[ F ] = 44.2 kN。 (1 分) M O x 0.8 F _ + 0.6 F

海南大学《工程力学(I)》试卷 2006年1月 5.(10分)利用叠加原理求图示等截面直梁中截面C的挠度和转角 q、人、EI均为已知。 解:(1)将梁等效转化为图示两种形式: B q (2分) (2)截面C的转角: 0.=0+0 (1分) 查附表得: 99 E7 (1分) (1分) a品贴 (1分)》 (3)截面C的挠度: w。=1+w (1分) 查附表得:
海南大学《工程力学(I)》试卷 2006 年 1 月 10 5.(10 分)利用叠加原理求图示等截面直梁中截面 C 的挠度和转角。 q、l、EI 均为已知。 解:(1)将梁等效转化为图示两种形式: (2 分) (2)截面 C 的转角: c = 1 + 2 (1 分) 查附表得: EI ql 6 3 1 = (1 分) EI ql EI l q B 6 48 ) 2 ( 3 3 2 = = − = − (1 分) EI ql EI ql EI ql c 48 7 6 48 3 3 3 = − = (1 分) (3)截面 C 的挠度: wc = w1 + w2 (1 分) 查附表得: A B C q A B C q A B C q 2 l 2 l