新疆大学：《材料力学》课程教学资源（教案讲义）第8章 组合变形

第八章组合变形 §81组合变形和叠加原理 §8.2拉伸或压缩与弯曲的组合 §8.4扭转与弯曲的组合变形 §8.1组合变形和叠加原理 1.基本变形：拉伸压缩、剪切、扭转、弯曲 2.组合变形：物件同时发生两种或两种以上基本变形情况称为 组合变形。 3.举例 1塔器一一压弯组合 2.钻床的立柱一一拉弯组合 3.皮带轮转动轴一一扭弯组合

第八章 组合变形 §8.1 组合变形和叠加原理 §8.2 拉伸或压缩与弯曲的组合 §8.4 扭转与弯曲的组合变形 §8.1 组合变形和叠加原理 1. 基本变形：拉伸压缩、剪切、扭转、弯曲. 2. 组合变形：物件同时发生两种或两种以上基本变形情况称为 组合变形。 3. 举例      皮带轮转动轴 — —扭弯组合 钻床的立柱 — —拉弯组合 塔器 — —压弯组合 3. 2. 1

2F 3F z/m少 4.组合变形分析方法（简化叠加） ①载荷的简化和分解，把物件上的外力转化成几组静力等效载 荷，其中每一组载荷对应着一种基本变形 ②分别计算每一基本变形各自引起的内力，应力应变和位移， 然后将所得结果叠加。 ③叠加法建立在叠加原理的基础上：即材料服从胡克定律，在小 变形前提下力与变形成线形关系。 §8.2拉伸或压缩与弯曲的组合 1.工程实例 1.钻床立柱 一一拉弯组合 2.压力机框架立柱一一拉弯组合 3.竖立塔器一一压弯组合 F 4.起重机的横梁一一压弯组合 F 2.注意：对受压弯组合的杆件，只适 Er B 用于杆件抗弯钢度较大的情况，才能用叠 加法去计算，否则只能按只能按纵横弯曲问题来计算

4.组合变形分析方法 （简化叠加） ① 载荷的简化和分解，把物件上的外力转化成几组静力等效载 荷，其中每一组载荷对应着一种基本变形。 ② 分别计算每一基本变形各自引起的内力，应力应变和位移， 然后将所得结果叠加。 ③ 叠加法建立在叠加原理的基础上：即材料服从胡克定律，在小 变形前提下力与变形成线形关系。 §8.2 拉伸或压缩与弯曲的组合 1.工程实例        起重机的横梁 — —压弯组合 竖立塔器 — —压弯组合 压力机框架立柱 — —拉弯组合 钻床立柱 — —拉弯组合 4. 3. 2. 1. 2. 注意：对受压弯组合的杆件，只适 用于杆件抗弯钢度较大的情况，才能用叠 加法去计算，否则只能按只能按纵横弯曲问题来计算

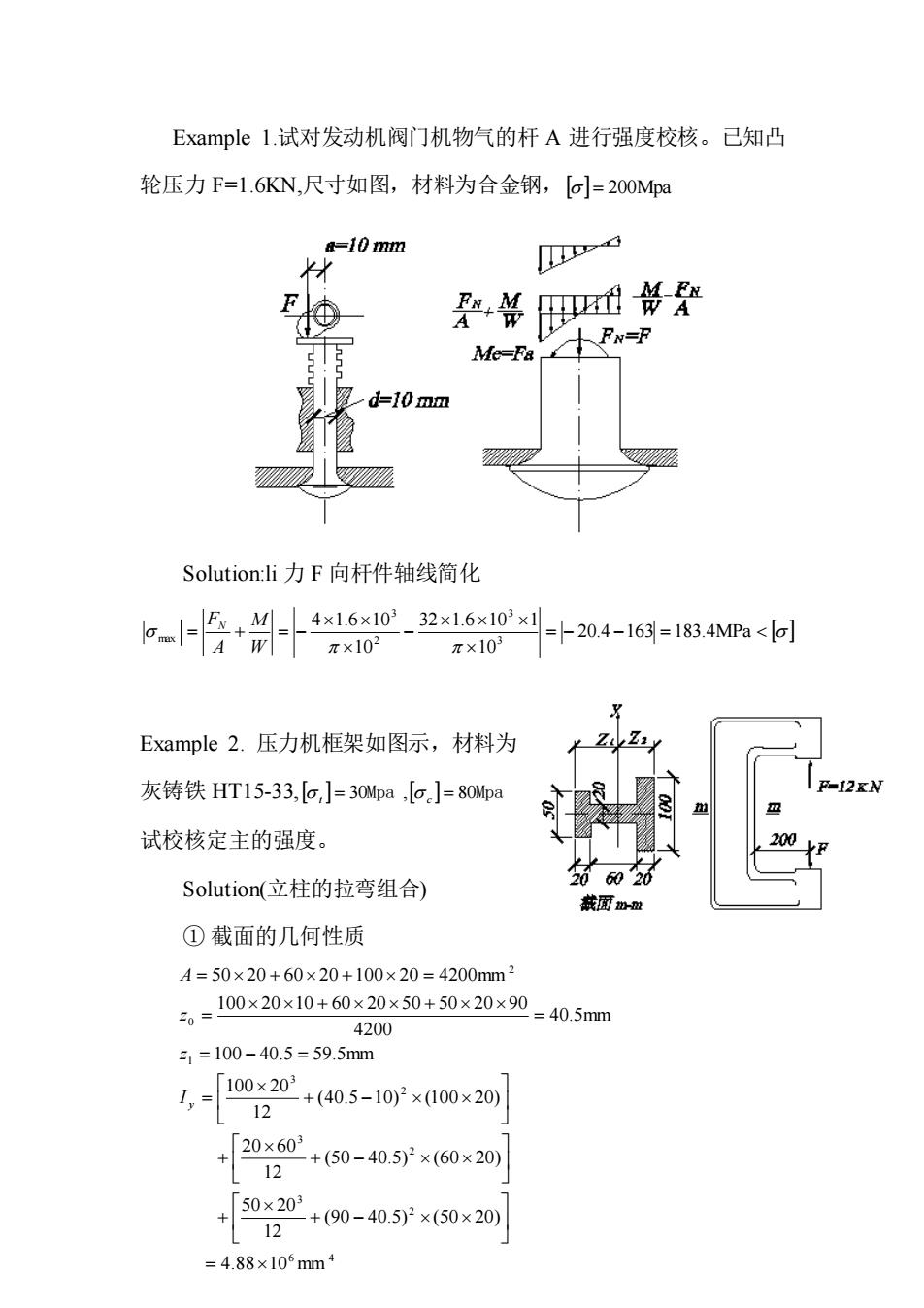
Example1.试对发动机阀门机物气的杆A进行强度校核。已知凸 轮压力F=1.6KN,尺寸如图，材料为合金钢，[a]=200M 4-10mm 0 Me-Fa d=10mm Solution:li力F向杆件轴线简化 -小作剑0 32×1.6×103×1 =卜20.4-163=183.4MPa<[o] π×103 Example2.压力机框架如图示，材料为 灰铸铁HT15-33,o,J=30Mpa,[o]=80Mp 试校核定主的强度。 Solution(立柱的拉弯组合) ①截面的几何性质 A=50×20+60×20+100×20=4200mm2 -100x20x10+60x20x50+50x20x90.405m 4200 51=100-40.5=59.5mm 1,=/100x20 12 +(40.5-10)2×100×20) +(50-40.5)2×(60×20) +50x20 +(90-40.5)2×(50×20) 12 =4.88×106mm

Example 1.试对发动机阀门机物气的杆 A 进行强度校核。已知凸 轮压力 F=1.6KN,尺寸如图，材料为合金钢，  = 200Mpa Solution:li 力 F 向杆件轴线简化     = − − =      −    = + = − 20.4 163 183.4MPa 10 32 1.6 10 1 10 4 1.6 10 3 3 2 3 max W M A FN Example 2. 压力机框架如图示，材料为 灰铸铁 HT15-33,  t  = 30Mpa , c  = 80Mpa 试校核定主的强度。 Solution(立柱的拉弯组合) ① 截面的几何性质 6 4 2 3 2 3 2 3 1 0 2 4.88 10 mm (90 40.5) (50 20) 12 50 20 (50 40.5) (60 20) 12 20 60 (40.5 10) (100 20) 12 100 20 100 40.5 59.5mm 40.5mm 4200 100 20 10 60 20 50 50 20 90 50 20 60 20 100 20 4200mm =        + −    +       + −    +       + −    = = − = =   +   +   = =  +  +  = y I z z A

②横截面H的内力 Fy=F=12KN M,=12×(200+40.5)×10-3=2.89kN·m ③强度校核 。+-2x +289x10x405=269MIPa<G,]=30MPa y 4200 4.88×105 a-.289x10×595.12x10 4.88×106 4200 =32.3MPa<[o]=80MPa §8.4扭转与弯曲的组合变形 扭转组合变形是机械工程中 L 最常见的情况，多数传动轴都属 Ma 于扭弯组合，对扭弯组合，在危 00060 险截面上危险点处的应力状态属 My 胚 于复杂应力状态，因此要进行强 FL 度校核，必须采用强度理论这里 Mz 首先推导（公论）扭弯组合变形的强度计算方法。 D D细 G V/Dz D 1.以圆轴为例 ①在危险截面：

②横截面 I-I 的内力 F N = F =12KN 12 (200 40.5) 10 2.89kN m 3 =  +  =  − M y ③强度校核 26.9MPa   30MPa 4.88 10 2.89 10 40.5 4200 12 10 6 3 6 =  =    +   = + = t N y o t m x Iy M Z A F   32.3MPa   80MPa 4200 12 10 4.88 10 2.89 10 59.5 3 6 6 1 =  =  −     = − = c N y y cm x A F I M Z   §8.4 扭转与弯曲的组合变形 扭转组合变形是机械工程中 最常见的情况，多数传动轴都属 于扭弯组合，对扭弯组合，在危 险截面上危险点处的应力状态属 于复杂应力状态，因此要进行强 度校核，必须采用强度理论这里 首先推导（公论）扭弯组合变形的强度计算方法。 1．以圆轴为例 ① 在危险截面：

M=M2YAX+ME max =M+M T=Me ②危险点处应力 ③危险点属于二向应力状态 ++r 02=0 。-受 ④危险点属应力复杂状态，必须用强度理论建立强度条件，对塑 性材料，可采用第三或第四强度理论。 o1-o3=[] 即： Vo2+3r2≤[ 或： a-o,广+a,-a,广+a,-os问 即： V62+3r2≤[6] 讨论： 上述公式为一般公式，虽然有圆轴为例推导 而得到，但适用用于轴，非圆轴的扭、弯，拉（压） 组合。只要应力状态如图示均可用。 ⑤圆轴扭弯组合的简化计算

2 max 2 M = M 2YAX + Mzmax = My max + Mz T = Me ② 危险点处应力        = = W M W T t   ③ 危险点属于二向应力状态 2 2 2 2 2 2 min max 4 2 1 2 ) 2 ( 2 ) 2 ( 2              + =  + =  + −  + =    x y x y ∴        = − + = = + + 2 2 3 2 2 2 1 4 2 1 2 0 4 2 1 2          ④危险点属应力复杂状态，必须用强度理论建立强度条件，对塑 性材料，可采用第三或第四强度理论。  − =   1 3 即：  +    2 2 3 或： ( −  ) + ( −  ) + ( −  )    2 3 1 2 2 3 2 1 2 2 1 即：  +    2 2 3 讨论： 上述公式为一般公式，虽然有圆轴为例推导 而得到，但适用用于轴，非圆轴的扭、弯，拉（压） 组合。只要应力状态如图示均可用。 ⑤ 圆轴扭弯组合的简化计算

1=2W m+T≤] W 式中m=M2+M √M2+0.75T -s[s] 可以校核，也可以设计截面尺寸。 Example图示传动轴，传递功率p=7.5kw,轴的转速=100rmin,AB 为皮带轮，A轮上的皮带为水平，B轮上的皮带为铅直，若两轮的直 径为600mm,则已知F)5,F2=1500N,轴材料的许用应力[g]=80MPa, 试按第三强度理论计算轴的直径。 24 Solution: 1D激 ①外力计算： k-959-59识-716Nm Me5.4KN B D 5.4KN G-5)x号=M, F3=1.5KN,F=3.89KN My/kN*m144 F+F3=5.39KN ②载荷简化及计算简图 Mz/kN*m M。=0 0.448 F×1200-5.4×800=0 1.39 T/kN'm F=3.6kN 0.716 M.=0

         = = = Wt W Wt T W M 2               +   + W M T W M T 2 2 2 2 0.75 式中 2 2 m = M y + ML 可以校核，也可以设计截面尺寸。 Example 图示传动轴，传递功率 p=7.5kw,轴的转速 n=100r/min,AB 为皮带轮，A 轮上的皮带为水平，B 轮上的皮带为铅直，若两轮的直 径为 600mm，则已知 F1 F2  ，F2=1500N，轴材料的许用应力  = 80MPa, 试按第三强度理论计算轴的直径。 Solution: ①外力计算： 716N m 100 7.5 = 9549. = 9549 =  n p Me 5.39KN 1.5KN, 3.89KN 2 ( ) 1 2 2 1 1 2 + = = = −  = F F F F M D F F e ②载荷简化及计算简图 D = 0 Fcz 1200−5.4800 = 0 Fcz=3.6kN  c = 0

FD2×1200-5.4×400=0FcD=1.8kN zMD=0Fgy×1200-5.4×250=0Fy=1.2kN M=0FDy×1200-5.4×1450=0FDw=6.52kN ③作弯矩图，扭矩图，确定危险截面 B截面： M=V1.442+0.4482=1.51KN.m T=0.716KN·m 心+T W √m2+T2=V1.512+0.7162=1.68kN.m d2滑9m

FDz 1200−5.4400 = 0 FCD=1.8kN D = 0 Fcy 1200−5.4250 = 0 Fcy=1.2kN  c = 0 FDy 1200−5.41450 = 0 FDy=6.52kN ③作弯矩图，扭矩图，确定危险截面 B 截面： T 0.716KN m 1.44 0.448 1.51KN m 2 2 =   = + =  ∵   + W M T 2 2 32 3 d w  = ∴ 1.51 0.716 1.68kN m 2 2 2 2 m +T = + =    59.8mm 32 1.68 3 =     d