轴向拉压应力与材料的力学性能 典型习题解析 1图示直杆截面为正方形,边长a=200mm,杆长L=4m,F=10kN,材料密度 p=20kN/m3.考虑杆的自重,计算1-1和2-2截面轴力,并画轴力图。 .8kN 1.6kN 71.6kN 12.4kN PN 3.2k (a (b) (c) (d) 题1图 解题分析:杆的自重为体积力。当杆件重量与外载荷大小在同一数量级时,应考虑杆自重对 内力、应力的影响。为画轴力图,要先计算一些特殊截面上的轴力,如集中力作用的截面和 A-A截面。 解:1、计算1-1截面轴力:从1-1截面将杆截成两段,研究上半段。设截面上轴力为F 为压力(见图b),则F、,应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大 小为二a2p,方向向下。于是由静力平衡条件∑F,=0得 -FN+2a2p=0 R1-片p-4x02m×02m×20x10Na3-800N 2、计算2-2截面轴力:从2-2截面将杆截成两段,研究上半段。设截面上轴力为F2, 为压力(见图c),则Fa应与该杆段所受外力平衡。杆段所受外力为杆段的自重和集中 力F,杆段自重为头。,方向向下。于是由静力平衡条件∑5,=0得 6
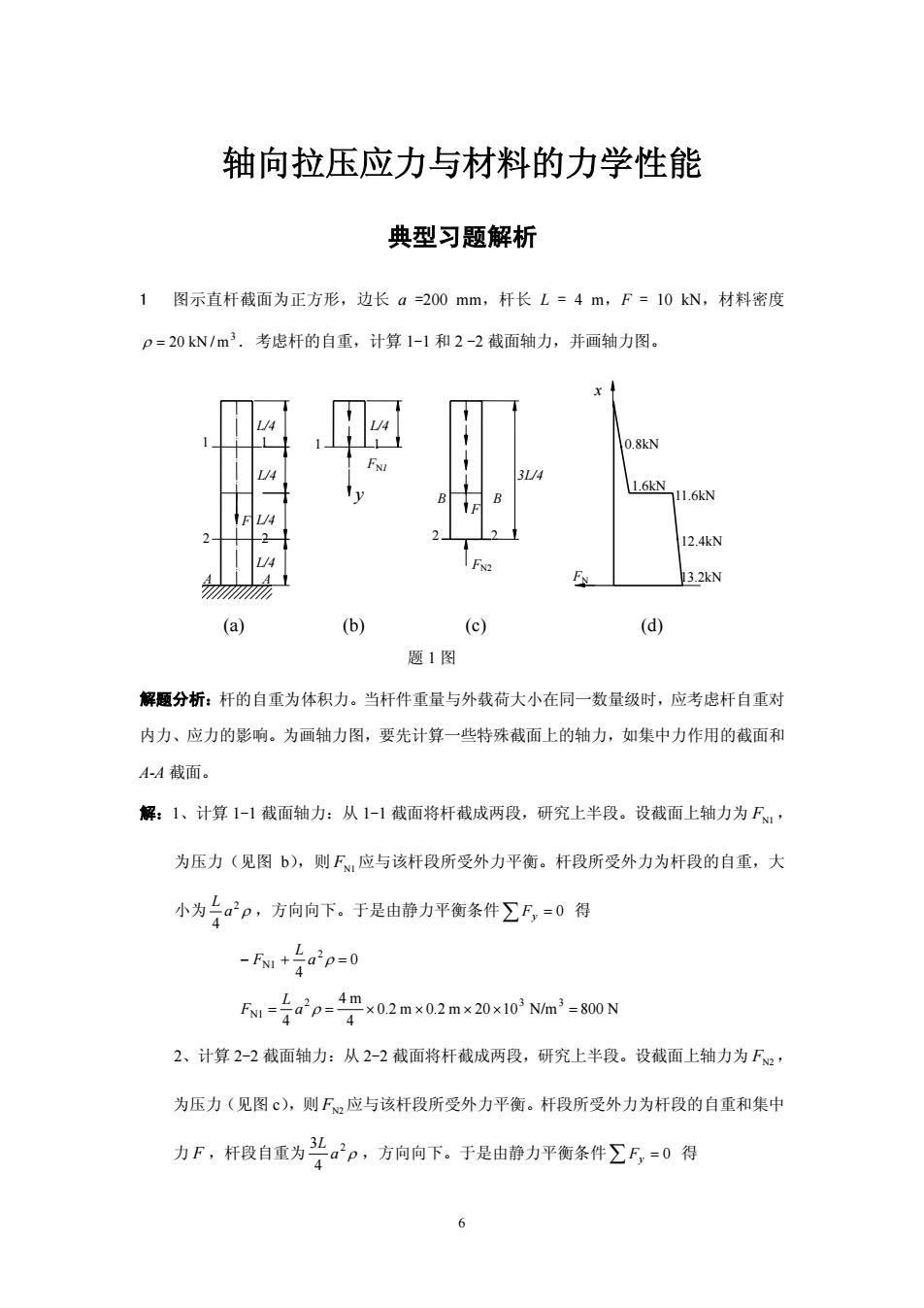
6 轴向拉压应力与材料的力学性能 典型习题解析 1 图示直杆截面为正方形,边长 a =200 mm,杆长 L = 4 m,F = 10 kN,材料密度 3 ρ = 20 kN / m . 考虑杆的自重,计算 1-1 和 2 -2 截面轴力,并画轴力图。 解题分析:杆的自重为体积力。当杆件重量与外载荷大小在同一数量级时,应考虑杆自重对 内力、应力的影响。为画轴力图,要先计算一些特殊截面上的轴力,如集中力作用的截面和 A-A 截面。 解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 , 为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大 小为 ρ2 4 a L ,方向向下。于是由静力平衡条件 ∑ = 0 Fy 得 0 4 2 − N1 + a ρ = L F 0.2 m 0.2 m 20 10 N/m 800 N 4 4 m 4 2 3 3 N1 = a ρ = × × × × = L F 2、计算 2-2 截面轴力:从 2-2 截面将杆截成两段,研究上半段。设截面上轴力为 FN2 , 为压力(见图 c),则 FN2 应与该杆段所受外力平衡。杆段所受外力为杆段的自重和集中 力 F ,杆段自重为 ρ2 4 3 a L ,方向向下。于是由静力平衡条件 ∑ = 0 Fy 得 FN1 (a) (b) (c) 题 1 图 F A 2 A L/4 FN2 2 L/4 L/4 y F 2 2 3L/4 (d) 12.4kN FN 13.2kN 11.6kN 1.6kN 1 L/4 L/4 1 1 1 0.8kN x B B

Ra=F+兰g2p=10x103N+34里x02mx02mx20x103Nam3=124x103N=124N 3、计算集中力F作用截面上的轴力:首先将杆沿力F作用截面(B-B)上侧截开,设 截面上轴力为压力F,研究上半部分杆段。由于只受本身重量作用,所以由静力平 衡条件得F作用截面上侧轴力为 然后将杆沿F作用截面(BB)下侧截开,设截面上轴力为压力Fg,研究上半部分 杆段。这时杆段受本身重量作用和集中力F作用,所以由静力平衡条件得F作用被面下侧 轴力为 r=5a2p+F=4"x02m2x20x103Nm3+10x102N=16×102N=16kN 4、计算A-A截面轴力:从A-A截面将杆被开,设截面上轴力为压力F,则F,应与该杆 上所有外力平衡。杆所受外力为杆的自重和集中力F,杆段自重为La'p,方向向下。于是 由静力平衡条件∑F,=0得 F4=F+La2p=10×103N+4m×0.2m×0.2m×20×103N/m3=13.2x103N=13.2kN 5、画轴力图:在坐标轴上标出特殊截面(杆的项截面、集中力F作用截面的上下侧和44 截面)处的轴力值,用直线连接即得轴力图(图d)。 讨论:(1)从轴力图看出,集中力作用的截面两侧轴力发生突变。突变值就是该集中力的大 小。(2)计算各截面轴力时,得到的轴力均为正值,这只说明真实轴力的方向与事先的假设 (本题均假设为压力)一致,并不意味着计算出的轴力为拉力。 2图示石柱桥墩,压力F=1000kN,石料密度p=25kN/m3,许用应力[a]=1MPa。试 比较下列三种情况下所需石料体积。(1)等截面石柱:(2)三段等长度的阶梯石柱:(3)等 强度石柱(柱的每个截面的应力都等于许用应力[σ])。 解题分析:设计这样的桥墩时,要考虑桥墩自重对强度的影响。可以想象,在桥域顶截面只 有压力F作用,轴力最小:在桥墩底截面,除压力F外,还承受桥墩本身重量,该处轴力 最大。当桥墩采用等截面石柱时,只要考虑底部截面的强度即可。如果采用阶梯型石柱,需 考虑每段的强度。如果要求各个截面强度相等,则需要对石柱的各截面进行特别设计。 解:1、采用等截面石柱 7
7 0.2 m 0.2 m 20 10 N/m 12.4 10 N 12.4 kN 4 3 4 m 10 10 N 4 3 2 3 3 3 3 N2 × × × × = × = × = + a ρ = × + L F F 3、计算集中力 F 作用截面上的轴力:首先将杆沿力 F 作用截面(B-B)上侧截开,设 截面上轴力为压力 + B FN ,研究上半部分杆段。由于只受本身重量作用,所以由静力平 衡条件得 F 作用截面上侧轴力为 (0.2 m) 20 10 N/m 1.6 10 N 1.6 kN 2 4 m 2 2 2 3 3 3 N + = a ρ = × × × = × = L F B 然后将杆沿 F 作用截面(B-B)下侧截开,设截面上轴力为压力 − B FN ,研究上半部分 杆段。这时杆段受本身重量作用和集中力 F 作用,所以由静力平衡条件得 F 作用截面下侧 轴力为 (0.2 m) 20 10 N/m 10 10 N 11.6 10 N 11.6 kN 2 4 m 2 2 2 3 3 3 3 N − = a + F = × × × + × = × = L F B ρ 4、计算 A-A 截面轴力:从 A-A 截面将杆截开,设截面上轴力为压力 FNA ,则 FNA 应与该杆 上所有外力平衡。杆所受外力为杆的自重和集中力 F ,杆段自重为 ρ2 La ,方向向下。于是 由静力平衡条件 ∑ = 0 Fy 得 10 10 N 4 m 0.2 m 0.2 m 20 10 N/m 13.2 10 N 13.2 kN 2 3 3 3 3 FNA = F + La ρ = × + × × × × = × = 5、画轴力图:在坐标轴上标出特殊截面(杆的顶截面、集中力 F 作用截面的上下侧和 A-A 截面)处的轴力值,用直线连接即得轴力图(图 d)。 讨论:(1)从轴力图看出,集中力作用的截面两侧轴力发生突变。突变值就是该集中力的大 小。(2)计算各截面轴力时,得到的轴力均为正值,这只说明真实轴力的方向与事先的假设 (本题均假设为压力)一致,并不意味着计算出的轴力为拉力。 2 图示石柱桥墩,压力 F = 1000 kN,石料密度 3 ρ = 25 kN / m ,许用应力[σ ] =1 MPa。试 比较下列三种情况下所需石料体积。(1)等截面石柱;(2)三段等长度的阶梯石柱;(3)等 强度石柱(柱的每个截面的应力都等于许用应力[σ ] )。 解题分析:设计这样的桥墩时,要考虑桥墩自重对强度的影响。可以想象,在桥墩顶截面只 有压力 F 作用,轴力最小;在桥墩底截面,除压力 F 外,还承受桥墩本身重量,该处轴力 最大。当桥墩采用等截面石柱时,只要考虑底部截面的强度即可。如果采用阶梯型石柱,需 考虑每段的强度。如果要求各个截面强度相等,则需要对石柱的各截面进行特别设计。 解:1、采用等截面石柱

如图a所示,设石柱横截面面积为A,长为人,底部截面轴力最大,其值为 Fx=F+dl 强度条件为 1000×103N 于是得4020N5m16m2 (a) b (dY 题2图 所用石料体积=A1=1.6m2x15m=24m3 2、采用三段等长度的阶梯石柱 结构如图b所示,按从上到下顺序,设各段横截面面积和长度分别为A,4,A,利 A,1,。显然,各阶梯段下端截面轴力最大,分别为 FNI=F+pdh,FN =F+phh+p:FN =F+pdh+pl+piyl3 由石柱的各段均应满足强度条件,于是得 1000×103N [110 Nm2510 Nm5m 42=e4台100x103N+25x102Nm2x4m5@131m 1x10°NWm2-25x103NWm3×5m 1-Etoth tath [o]-p13 100x103N+25x103Nam3×1.14m2×5m+25x102Nm3×131m2×5m-149m 1x106N/m2-25x103NWm3×5m 所用石料体积为2=(4+42+4儿=1.14m2+131m2+1.49m2)×5m=19.7m3 3、采用等强度石柱 8
8 如图 a 所示,设石柱横截面面积为 A,长为 l,底部截面轴力最大,其值为 FN = F + ρAl 强度条件为 [ ] N ρ σ ρ σ = + ≤ + = = l A F A F Al A F 于是得 2 6 2 3 3 3 1.6 m 1 10 N/m 25 10 N/m 15 m 1000 10 N [ ] = × − × × × = − = l F A σ ρ 所用石料体积 2 3 V1 = Al = 1.6 m ×15 m = 24 m 2、采用三段等长度的阶梯石柱 结构如图 b 所示,按从上到下顺序,设各段横截面面积和长度分别为 1 1 A , l , 2 2 A , l 和 3 3 A , l 。显然,各阶梯段下端截面轴力最大,分别为 N1 1 1 F = F + ρA l , N2 1 1 2 2 F = F + ρA l + ρA l , N3 1 1 2 2 3 3 F = F + ρA l + ρA l + ρA l 由石柱的各段均应满足强度条件,于是得 2 6 2 3 3 3 1 1 1.14 m 1 10 N/m 25 10 N/m 5 m 1000 10 N [ ] = × − × × × = − = l F A σ ρ 2 6 2 3 3 3 3 3 2 2 1 1 2 1.31 m 1 10 N/m 25 10 N/m 5 m 1000 10 N 25 10 N/m 1.14 m 5 m [ ] = × − × × × + × × × = − + = l F A l A σ ρ ρ 2 6 2 3 3 3 3 3 2 3 3 2 3 1 1 2 2 3 1.49m 1 10 N/m 25 10 N/m 5 m 1000 10 N 25 10 N/m 1.14 m 5 m 25 10 N/m 1.31 m 5 m [ ] = × − × × × + × × × + × × × = − + + = l F A l A l A σ ρ ρ ρ 所用石料体积为 2 2 2 3 V2 = (A1 + A2 + A3 )l1 = (1.14 m +1.31 m +1.49 m )×5 m = 19.7 m 3、采用等强度石柱 5m dx x (a) (b) (c) (d) 题 2 图 [σ] [σ] ρA(x)dx F F F 5m 5m 15m

所谓等强度石柱,即要求每一个横截面上的应力都等于许用应力[]。取x坐标如图 c所示,则根据等强度要求,有 at-5围-o A(x) 由于不同截面上轴力不同,因而横截面面积必须随x坐标变化才能满足上式。为确 定横截面面积随x坐标的变化规律,在石柱中x处取女微段,设微段上截面的面积为 Ax),则下截面的面积为Ax+d4(x),微段石柱的受力情况如图d所示。 考虑微段的静力平衡,有 【4(x)+d4x-o]=4Axo]+p4(x)d d4x[a]=a4x)d出 局 设桥域顶端截面(x=0)的面积为A。,对上式积分,得x截面的面积为 Ax)=4exp向 于4奇1m 石柱下发截面积40=么e四的=1m×p学 =145m2 石柱的体积可由积分求得。也可用下面的简便方法求解: 石柱下端截面的轴力FN)=F+G,式中G为石柱的自重,G=p乃 由石柱的下端截面强度条件得 G=[o]40-F 所以石柱体积为5=9=回40-E.10Pn145m2-10o0×10N-18m 25×103NWm3 三种情况下所需石料的体积比值为24:19.7:18,或1.33:1.09:1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3滑轮结构如图,AB杆为钢材,截面为圆形,直径d=20mm,许用应力[o]=160MPa,BC 杆为木材,截面为方形,边长a=60mm,许用应力cJ=l2MPa。试计算此结构的许用载
9 所谓等强度石柱,即要求每一个横截面上的应力都等于许用应力[σ ] 。取 x 坐标如图 c 所示,则根据等强度要求,有 [ ] ( ) ( ) ( ) N σ = = σ A x F x x 由于不同截面上轴力不同,因而横截面面积必须随 x 坐标变化才能满足上式。为确 定横截面面积随 x 坐标的变化规律,在石柱中 x 处取 dx 微段,设微段上截面的面积为 A(x),则下截面的面积为 A(x)+dA(x),微段石柱的受力情况如图 d 所示。 考虑微段的静力平衡,有 [A(x) + dA(x)]⋅[σ ] = A(x)[σ ] + ρA(x)dx dA(x)[σ ] = ρA(x)dx x A x A x d ( ) [ ] d ( ) σ ρ = 设桥墩顶端截面( x = 0)的面积为 A0 ,对上式积分,得 x 截面的面积为 x A x A [ ] 0 ( ) exp σ ρ = 由于 2 6 2 3 0 1 m 1 10 N/m 1000 10 N [ ] = × × = = σ F A 石柱下端截面积 1 10 N/m 2 25 10 N/m 15 m [ ] 2 ( ) 0 exp 1m exp 1.45 m 6 2 3 3 = = × = × × × σ ρ l A l A 石柱的体积可由积分求得。也可用下面的简便方法求解: 石柱下端截面的轴力 FN (l) = F + G ,式中 G 为石柱的自重,G = ρV3 由石柱的下端截面强度条件得 [ ] ( ) σ = σ + = A l F G G = [σ ]A(l) − F 所以石柱体积为 3 3 3 6 2 3 3 18 m 25 10 N/m [ ] ( ) 1 10 Pa 1.45 m 1000 10 N = × × × − × = − = = ρ σ ρ G A l F V 三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20mm,许用应力[σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60mm ,许用应力[ ] 12 MPa σ c = 。试计算此结构的许用载

荷[F]。 解题分析:使各杆均满足强度条件的载荷即为许用载 荷。首先计算F作用下各杆轴力,然后利用各杆的强 度条件确定许用载荷[F门]。两根杆确定出两个可能不 同的[F],取其中的小值即为结构的许用载荷。 解:1、计算AB和BC两杆轴力FN4B和FN.C 取图示坐标系,并设AB杆受拉,BC杆受压, 题3图 则B点的静力平衡方程为 ∑F=0N.cos30°-fN.sim60°=0,得FN.B=FN.BC ∑F,=0FX,C·sin30°+FN,Bc0s60°-2F=0,得,B=F.C=2F 2、确定AB杆可以承担的载荷 F.B=2F≤6lAw=160x10Pa×20x103m2=503x102N 4 旧1=03x102N-2515×102N=2515kN 3、确定BC杆可以承担的载荷 FN.Bc=2F≤o.4c=12×106Pa×(60x10-3m)2=43.2x103N M=432x102N-216x10N=216kN 两者取小值,所以结构的许用载荷[F]为21.6kN 4两块钢板用直径d=20mm铆钉搭接。先采用两种搭接形式,分别如图a、图b所示。已知 F-160kN,两板尺寸相同,厚度6=10mm,宽度b-120mm,铆钉和钢板材料相同,许用 切应力r=140MPa,许用挤压应力[os=320MPa,许用拉应力[aJ=60MPa。试计算所 需的铆钉数,并从强度角度比较两种搭接形式的优劣,校核板的拉伸强度。 解题分桥:本题需要考虑下面强度问题:铆钉的剪切强度和挤压强度,钢板的拉伸强度。一 方面,较多数目的铆钉可以提高铆钉强度,另一方面,较多铆钉数意味者较多铆钉孔,可能 会降低钢板的拉伸强度。而铆钉孔对钢板拉伸强度的影响,表现在铆钉孔减小了钢板的横截 面面积。可以想象,如果将几个铆钉孔沿横向排成一排,对钢板强度最为不利。所以铆钉孔 排列方式,也影响到钢板强度。 解:首先假设不论什么排列方式,各个铆钉承受相同的载荷。设所需铆钉数为”,则每个 公
10 荷[F]。 解题分析:使各杆均满足强度条件的载荷即为许用载 荷。首先计算 F 作用下各杆轴力,然后利用各杆的强 度条件确定许用载荷[F]。两根杆确定出两个可能不 同的[F],取其中的小值即为结构的许用载荷。 解:1、计算 AB 和 BC 两杆轴力 FN,AB 和 FN, BC 取图示坐标系,并设 AB 杆受拉,BC 杆受压, 则 B 点的静力平衡方程为 0 cos 30 sin 60 0 ∑Fx = FN, BC ⋅ ° − FN , AB ⋅ ° = ,得 FN , AB = FN , BC 0 sin 30 cos 60 2 0 ∑Fy = FN , BC ⋅ ° + FN , AB ⋅ ° − F = ,得 FN , AB = FN , BC = 2F 2、确定 AB 杆可以承担的载荷 [ ] 50.3 10 N 4 π (20 10 m) 2 160 10 Pa 3 -3 2 6 N = × × F ,AB = F ≤ σ ⋅ AAB = × × 25.15 10 N 25.15kN 2 50.3 10 N [ ] 3 3 = × = × F = 3、确定 BC 杆可以承担的载荷 2 [ ] 12 10 Pa (60 10 m) 43.2 10 N 6 3 2 3 N = ≤ c ⋅ = × × × = × − F ,BC F σ ABC 21.6 10 N 21.6 kN 2 43.2 10 N [ ] 3 3 = × = × F = 两者取小值,所以结构的许用载荷[F]为 21.6 kN。 4 两块钢板用直径 d = 20 mm 铆钉搭接。先采用两种搭接形式,分别如图a、图b所示。已知 F = 160kN ,两板尺寸相同,厚度δ =10 mm,宽度b = 120mm ,铆钉和钢板材料相同,许用 切应力[τ ] = 140 MPa,许用挤压应力[ ] 320MPa σ bs = ,许用拉应力[ ] σ t =160 MPa。试计算所 需的铆钉数,并从强度角度比较两种搭接形式的优劣,校核板的拉伸强度。 解题分析:本题需要考虑下面强度问题:铆钉的剪切强度和挤压强度,钢板的拉伸强度。一 方面,较多数目的铆钉可以提高铆钉强度,另一方面,较多铆钉数意味着较多铆钉孔,可能 会降低钢板的拉伸强度。而铆钉孔对钢板拉伸强度的影响,表现在铆钉孔减小了钢板的横截 面面积。可以想象,如果将几个铆钉孔沿横向排成一排,对钢板强度最为不利。所以铆钉孔 排列方式,也影响到钢板强度。 解:首先假设不论什么排列方式,各个铆钉承受相同的载荷。设所需铆钉数为 n ,则每个 题 3 图 y 60. 600 FN,BC FN,AB F x F C A B

锦钉所受剪力为5-片,挤压力爪=5。 1、按剪切强度条件确定铆钉数:设铆钉横截面面积为4,则铆钉的剪切强度条件为 总啊 4F 4×160×102N 于是得m≥日x20x10P9010Nm-364 2、按挤压强度条件确定铆钉数:挤压面面积A=6d,铆钉挤压强度条件为 ←小 160×103N 10x10-m2010m 320x10 Nm5 两者取大值,最后确定铆钉数n=4。 3、钢板拉伸强度校核:分别按图a和图b排列方式,画出钢板轴力图如图示。 按图a排列,1-1截面为危险截面,拉应力为 o-号-76”00-2x32020i0x40a2N>a F 160×103N 0 中2 88 1121 88 1 12 2 34 (a) 题4图 所以,按图ā方式排列铆钉时,不满足钢板拉伸强度要求。 若按图b排列,则1-1被面的拉应力为
11 铆钉所受剪力为 n F FS = ,挤压力 n F Fb = 。 1、按剪切强度条件确定铆钉数:设铆钉横截面面积为A,则铆钉的剪切强度条件为 [ ] π 4 2 S τ = = ≤ τ n d F A F 于是得 3.64 π 20 10 m) 140 10 N/m 4 160 10 N π [ ] 4 3 2 6 2 3 2 = × × × × × × ≥ = ( − d τ F n 2、按挤压强度条件确定铆钉数:挤压面面积 A = δ d ,铆钉挤压强度条件为 [ ] b s b s b bs σ δ σ = = ≤ n d F A F 得 2.5 10 10 m 20 10 m 320 10 N/m 160 10 N [ ] 3 3 6 2 3 bs = × × × × × × ≥ = − − δ d σ F n 两者取大值,最后确定铆钉数 n = 4。 3、钢板拉伸强度校核:分别按图 a 和图 b 排列方式,画出钢板轴力图如图示。 按图 a 排列,1-1截面为危险截面,拉应力为 200MPa [ ] 120 2 20 10 m 10 10 m 160 10 N 2 3 3 3 1 1 σ δ σ = > − × × × × × = − = = − ( ) ( ) − − b d F A F 所以,按图 a 方式排列铆钉时,不满足钢板拉伸强度要求。 若按图b排列,则1-1截面的拉应力为 2 2 F 1 1 F F F F F F F FN (a) F 1 1 F F 3F/4 F x F/2 FN (b) F/4 x 题 4 图

160×103N 2-2截面上的拉应力为 3F 3×160x103N 4K6-204120-2×20x10mX10x10-n150Mm<] 所以,按图b方式排列铆钉时,满足钢板拉伸强度要求。 比较两种排列方式,图b中的排列方式较合理,因为这种排列方式在轴力较大的截面 配置较少的铆钉孔,在轴力较小的藏面配置较多的铆钉孔,从而降低最大拉伸应力值 讨论:铆钉排列方式虽然对铆钉本身强度无影响,但却对钢板的拉伸强度影响较大。所以, 在工程中,从被连接件的拉伸强度考虑,铆钉一般按菱形挂列
12 160MPa [ ] 120 20 10 m 10 10 m 160 10 N 3 3 3 1 1 1 1 σ δ σ = = − × × × × = − = = − − − (b d) ( ) F A F 2-2截面上的拉应力为 150MPa [ ] 4 120 2 20 10 m 10 10 m 3 160 10 N 4 2 4 3 3 3 3 3 2 2 2 σ δ σ = < − × × × × × × = − = = − − − (b d) ( ) F A F 所以,按图 b 方式排列铆钉时,满足钢板拉伸强度要求。 比较两种排列方式,图 b 中的排列方式较合理,因为这种排列方式在轴力较大的截面 配置较少的铆钉孔,在轴力较小的截面配置较多的铆钉孔,从而降低最大拉伸应力值。 讨论:铆钉排列方式虽然对铆钉本身强度无影响,但却对钢板的拉伸强度影响较大。所以, 在工程中,从被连接件的拉伸强度考虑,铆钉一般按菱形排列