
第五章弯曲应力 §5.1纯弯曲 §52纯弯曲时的正应力 §5-3横力弯曲(剪切弯曲)时的正应力 §5.4弯曲切应力 §5.6提高弯曲强度的措施 §5.1纯弯曲 有德时am0 M 2.观察变形 以矩形截面梁为伤例 (1)变形前的直线aa、bb变形后 成为曲线a'a、b'b,变形前的mm,m变形后仍为直线m'm、m'n,然 而却相对转过了一个角度,且仍与a'a、b'b曲线相垂直。 (2)平面假设 根据实验结果,可以假设变形前原为平 b 面的梁的横截面变形后仍为平面,且仍垂直 m△ 于变形后的梁轴线,这就是弯曲变形的平面 假设。 m (3)设想 设想梁是由平行于轴线的众多纤维组 m 成。在纯弯曲过程中各纤维之间互不挤压, 只发生伸长和缩短变形。显然,凸边一侧的纤维发生伸长,凹边一侧的 纤维缩短。由平面假设纤维由伸长变为缩短,连续变化,中间一定有一 层纤维称既不伸长,也不缩短,这一层纤维为中性层
第五章 弯曲应力 §5.1 纯弯曲 §5.2 纯弯曲时的正应力 §5-3 横力弯曲(剪切弯曲)时的正应力 §5.4 弯曲切应力 §5.6 提高弯曲强度的措施 §5.1 纯弯曲 1. − − = = = − − 0, , 0, , F M const F M S S 纯弯曲 横力弯曲 弯曲 2.观察变形 以矩形截面梁为例 (1)变形前的直线 aa、bb 变形后 成为曲线 a a 、bb ,变形前的 mm ,nn 变形后仍为直线 m m 、m n ,然 而却相对转过了一个角度,且仍与 a a 、bb 曲线相垂直。 (2)平面假设 根据实验结果,可以假设变形前原为平 面的梁的横截面变形后仍为平面,且仍垂直 于变形后的梁轴线,这就是弯曲变形的平面 假设。 (3)设想 设想梁是由平行于轴线的众多纤维组 成。在纯弯曲过程中各纤维之间互不挤压, 只发生伸长和缩短变形。显然,凸边一侧的纤维发生伸长,凹边一侧的 纤维缩短。由平面假设纤维由伸长变为缩短,连续变化,中间一定有一 层纤维称既不伸长,也不缩短,这一层纤维为中性层。 F Fa F a a m n a m n a b b m' n' a' a' b' b' m' n' △
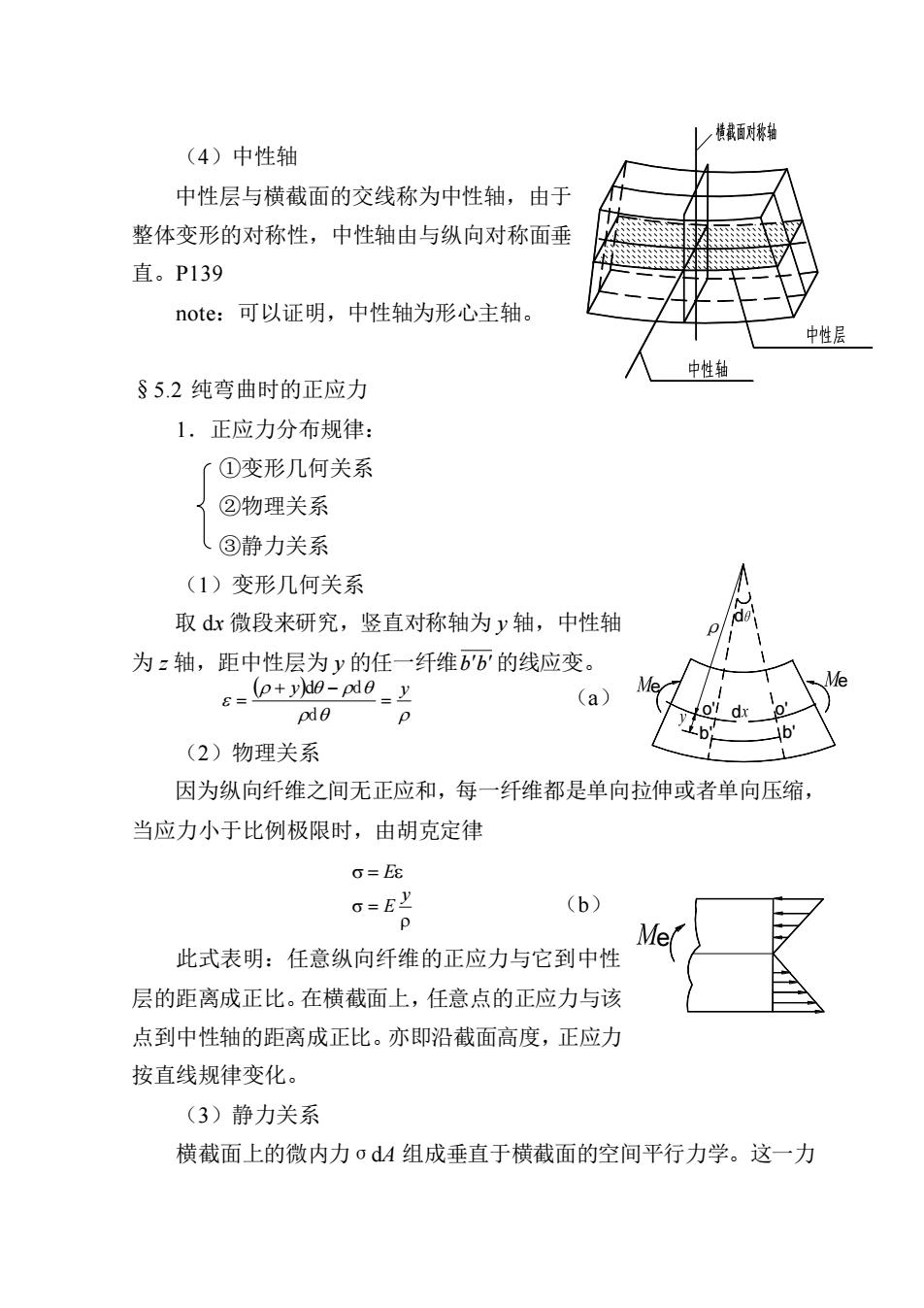
,播慧百对者钻 (4)中性轴 中性层与横截面的交线称为中性轴,由于 整体变形的对称性,中性轴由与纵向对称面垂 直。P139 note:可以证明,中性轴为形心主轴。 中性层 中性轴 §5.2纯弯曲时的正应力 1.正应力分布规律: (①变形几何关系 ②物理关系 、③静力关系 (1)变形几何关系 取dr微段来研究,竖直对称轴为y轴,中性轴 为:轴,距中性层为y的任一纤维b的线应变。 E=p+0-N0=y (a) P o'l dx b b (2)物理关系 因为纵向纤维之间无正应和,每一纤维都是单向拉伸或者单向压缩, 当应力小于比例极限时,由胡克定律 G=Ee =昭 (b) Me 此式表明:任意纵向纤维的正应力与它到中性 层的距离成正比。在横截面上,任意点的正应力与该 点到中性轴的距离成正比。亦即沿截面高度,正应力 按直线规律变化。 (3)静力关系 横截面上的微内力σd4组成垂直于横截面的空间平行力学。这一力
(4)中性轴 中性层与横截面的交线称为中性轴,由于 整体变形的对称性,中性轴由与纵向对称面垂 直。P139 note:可以证明,中性轴为形心主轴。 §5.2 纯弯曲时的正应力 1.正应力分布规律: ①变形几何关系 ②物理关系 ③静力关系 (1)变形几何关系 取 dx 微段来研究,竖直对称轴为 y 轴,中性轴 为 z 轴,距中性层为 y 的任一纤维 bb 的线应变。 ( ) y y = + − = d d d (a) (2)物理关系 因为纵向纤维之间无正应和,每一纤维都是单向拉伸或者单向压缩, 当应力小于比例极限时,由胡克定律 = E = y E (b) 此式表明:任意纵向纤维的正应力与它到中性 层的距离成正比。在横截面上,任意点的正应力与该 点到中性轴的距离成正比。亦即沿截面高度,正应力 按直线规律变化。 (3)静力关系 横截面上的微内力σdA 组成垂直于横截面的空间平行力学。这一力 e e ρ d d o' o' b' b' e

系可能简化为三个内力分量: F=otA Me Mn=∫:oA M.=yodA 横截面上的内力与截面左侧的外力必须 平衡。在纯弯曲情况下,截面左侧的外力只有 对z轴的力偶矩M。由于内外力必须满足平衡 方程,故: ① ΣF=0 FN=JodA=0 式(b)代入式(c) 4-54-0 0 Ju4=S2=0 结论:Z轴(中性轴)通过形心。 ② M,=0 Mi==oA=0 (d) 式(b)代入式(d) a4=月d4=0 ydA=1.=0 结论:y轴为对称轴,上式自然满足 EM,=0 M.=M=M=∫yoiA(e) 式(b)代入式(e) M=aA=∫yra4 (f) S.ydA=1z ∴式(D可写成 P Elz (g)
系可能简化为三个内力分量: = = = A iz A iy A M y A M z A F A d d d 横截面上的内力与截面左侧的外力必须 平衡。在纯弯曲情况下,截面左侧的外力只有 对 z 轴的力偶矩 Me。由于内外力必须满足平衡 方程,故: ① = = = A Fx 0 F dA 0 (c) 式(b)代入式(c) = = A A y A E dA d 0 ∵ 0 = E const E ∴ = = A A SZ yd 0 结论:Z 轴(中性轴)通过形心。 ② = = = A M y 0 Miy zdA 0 (d) 式(b)代入式(d) = = A A yz A E z dA d 0 = = A yzdA I yz 0 结论:y 轴为对称轴,上式自然满足 ③ = = = = A M z 0 Me Miz M ydA (e) 式(b)代入式(e) = = A A y A E M y dA d 2 (f) ∵ = A Z y dA I 2 ∴式(f)可写成 EI Z M = 1 (g) e d

式中上为梁轴线变形后的曲率,称为梁的抗弯刚度。 2.纯弯曲时梁的正应力计算公式 由式(g)和式(b)中消去得 M. 讨论:(1)导出公式时用了矩形截面,但未涉及任何矩形的几何特 性,因此,公式具有普遍性。 (2)只要梁有一纵向对称面,且载荷作用于对称面内,公式都适用。 (3)横截上任一点处的应力是拉应力还是压应力可直接判定,不需 用y坐标的正负来判定。 §5-3横力弯曲(剪切弯曲)时的正应力 1.纯弯曲正应力公式推广应用于横力弯曲 a=M.y 12 讨论:公式的适用条件 (1)平面弯曲 (2)纯弯曲或h5的横力弯曲(0,τ) (3)应力小于比例极限。 2.最大正应力 =My' 1z 引入记号: 形s上 ymx 6m=w2 W一一抗弯截面系数(m3) 讨论:
式中 1 为梁轴线变形后的曲率,EIZ 称为梁的抗弯刚度。 2.纯弯曲时梁的正应力计算公式 由式(g)和式(b)中消去 1 得 z y I M = 讨论:(1)导出公式时用了矩形截面,但未涉及任何矩形的几何特 性,因此,公式具有普遍性。 (2)只要梁有一纵向对称面,且载荷作用于对称面内,公式都适用。 (3)横截上任一点处的应力是拉应力还是压应力可直接判定,不需 用 y 坐标的正负来判定。 §5-3 横力弯曲(剪切弯曲)时的正应力 1.纯弯曲正应力公式推广应用于横力弯曲 Z I M y = 讨论:公式的适用条件 (1)平面弯曲 (2)纯弯曲或 l/h≥5 的横力弯曲(σ,τ) (3)应力小于比例极限。 2.最大正应力 Z I M y max max max = 引入记号: max y I W Z Z = WZ M max max = W——抗弯截面系数(m3) 讨论:

(1)等直梁而言·x发生在最大弯矩断面,距中性轴最远处yax。 (2)对于变截面梁不应只注意最大弯矩Mmx截面,而应综合考虑 弯矩和抗弯截面系数W2两个因素。 3.强度条件 _M≤o] 0m=W2 (1)对抗拉抗压强度相同的材料,只要 la≤o]即可 (2)对抗拉抗压强度不等的材料(如铸铁)则应同时满足: o,m≤o, 4.强度计算 (1)强度校核 2)设计截面尺寸:,2同 、Mm (3)确定许用载荷:M≤oW Example1空气泵操作杆,右端受力F=8.5kN,1-l、2-2截面相同, 均为hb=3的矩形,若o=50MPa,试选用1-1、2-2截面尺寸。 Solution ①求F2 M。=0 0.38F,-8.5×0.72=0 F3=16.1kN ②求截面弯矩 M=8.5×(0.72-0.08=5.44kNm M2=16.1×(0.38-0.08)=4.38kNm 故: M=M =5.44kN.m
(1)等直梁而言σmax发生在最大弯矩断面,距中性轴最远处 ymax。 (2)对于变截面梁不应只注意最大弯矩 Mmax截面,而应综合考虑 弯矩和抗弯截面系数 WZ 两个因素。 3.强度条件 [ ] max max = WZ M (1)对抗拉抗压强度相同的材料,只要 max 即可 (2)对抗拉抗压强度不等的材料(如铸铁)则应同时满足: c c t t max max 4.强度计算 (1)强度校核 (2)设计截面尺寸: M max WZ (3)确定许用载荷: Mmax WZ Example1 空气泵操作杆,右端受力 F1=8.5kN,1-1、2-2 截面相同, 均为 h/b=3 的矩形,若[σ]=50MPa,试选用 1-1、2-2 截面尺寸。 Solution ①求 F2 M 0 = 0 0.38F2 − 8.5 0.72 = 0 F2 = 16.1 kN ②求截面弯矩 M1=8.5×(0.72-0.08)=5.44kN·m M2=16.1×(0.38-0.08)=4.38kN·m 故: Mmax = M1 = 5.44 kN·m

③设计截面 %行5ar-10m时 50 h=3b b≥10e8x0-417mm 3 h=125mm §5.4弯曲切应力 动- dr 切应力的分布规律与梁的横截面形状有关,因此以梁的横截面形状 不同分别加以讨论。 1.矩形截面梁 (1)切应力的分布规律 假设彻应力的方向与剪力厂平行 切应力沿截面宽度均匀分布 当h>b时,按上述假设得到的解答与精确解 相比有足够的准确度。 (2)切应力沿截面高度的变化规律 ①从梁中取出dr段,而微段上无载荷作用。 ②截面上的o和τ的分布如图 ③研究微块的平衡
③设计截面 5 6 1 088 10 50 5 44 10 = = . M . W max Z mm3 2 6 12 2 3 max h bh bh y I W Z Z = = = ∵ 5 2 1 088 10 2 3 = 3 = . b h b Wz mm3 41 7 3 2 1 088 10 3 3 . . b = mm ∴ h=125mm §5.4 弯曲切应力 − − FS M 横力弯曲 切应力的分布规律与梁的横截面形状有关,因此以梁的横截面形状 不同分别加以讨论。 1.矩形截面梁 (1)切应力的分布规律 切应力 沿截面宽度均匀分布 切应力 的方向与剪力 平行 假设 FS 当 h>b 时,按上述假设得到的解答与精确解 相比有足够的准确度。 (2)切应力沿截面高度的变化规律 ①从梁中取出 dx 段,而微段上无载荷作用。 ②截面上的σ和τ的分布如图 ③研究微块的平衡 d m n m n d d ' m n

F-oMdd Iz .M+amfd⅓A (a) I。 (M+dM)s 式中:S=∫yd4为离中性轴为y的横线以下面积对中性轴之静矩。 =40a4=兴1a4签 (b) 考虑到微块顶面上相切的内力系的合 力 dFs=t'bdx (c) F,=0 FN2 -FNI-dFs=0 (d) 式(a)、(b)、(c)代入式(d) ±dws-4s-adx=0(e) r'=dM s: dx I b (d) 出6 (f) 由切应力互等定理,横截面上Pq线处切应力为 (g) I,b 这就是矩形截面梁弯曲切应力计算公 式 ④讨论: α.横力弯曲下梁的纵向纤维层之间存在 A=bdy 切应力 b.矩形截面如图 dM=,s-d4-年-yor
( ) ( ) * 1 * * 1 2 * Z A Z A A Z S I M M y A I M M A I M M y F A d d d d d d + = + = + = = (a) 式中: = * 1 * A Sz y dA 为离中性轴为 y 的横线以下面积对中性轴之静矩。 Z z A Z A Z A I MS y A I M A I My F A * * 1 * 1 * 1 = = = = d d d (b) 考虑到微块顶面上相切的内力系的合 力 F b x d S = d ' (c) 0 0 ' Fx = F2 − F1 − dFS = (d) 式(a)、(b)、(c)代入式(d) ( ) 0 * * − − = + S b x I M S I M M z Z Z d d (e) I b S x M Z Z * d d = (d) ∵ FS x M = d d ∴ I b F S Z * S Z = (f) 由切应力互等定理,横截面上 pq 线处切应力为 I b F S Z S Z * = (g) 这就是矩形截面梁弯曲切应力计算公 式。 ④讨论: a. 横力弯曲下梁的纵向纤维层之间存在 切应力 b. 矩形截面如图 1 dA = bdy = = = − / 2 2 2 1 1 * 1 * 2 4 h A y Z y b h S y dA by dy or

父“w*9训-岭n均列行-力 说明切应力τ沿截面高度按抛物线规律变化。 c.当y=±时,t=0 当时密 日考越到管 2.工字形截面梁 (1)计算表明:截面上剪力F的95~97% 由腹板承担,故只考虑腹板上的切应力分布规 律,而腹板是一个狭长矩形,矩形截面切应力 两个假设均适用(t方向与F一致,设宽度 均布),采用矩形截面方法可得: r=hs Izb。 式中:e-成+作-y小 以y0=士经代入上式得 ag-冷] Fs bh2 bh m=1,b88
∴ 说明切应力τ沿截面高度按抛物线规律变化。 c. 当 2 h y = 时,τ=0 当 y=0 时, Z S I F h 8 2 = max = d. 考虑到 12 3 bh I Z = bh F bh FS S = =1.5 2 3 max 2.工字形截面梁 (1)计算表明:截面上剪力 FS 的 95~97% 由腹板承担,故只考虑腹板上的切应力分布规 律,而腹板是一个狭长矩形,矩形截面切应力 两个假设均适用(τ方向与 FS 一致,设宽度 均布),采用矩形截面方法可得: 0 * I b F S Z S Z = 式中: ( ) = − + − 2 2 2 0 0 0 * 2 8 2 4 y b h h h b S Z ( ) = − + − 2 2 2 0 0 0 2 0 8 2 4 y b h h h b I b F Z S 以 y=0, 2 h0 y = 代入上式得 ( ) = − − 8 8 2 0 0 2 0 max h b b bh I b F Z S = − 8 8 2 0 2 0 min bh bh I b F Z S ) 4 ( 2 ) 2 ( 2 1 ) 2 )] ( 2 ( 2 1 * [ 2 2 * y b h y h y h y b h S A y z = + − = − + = − max h h = − 2 2 2 2 4 y h I FS
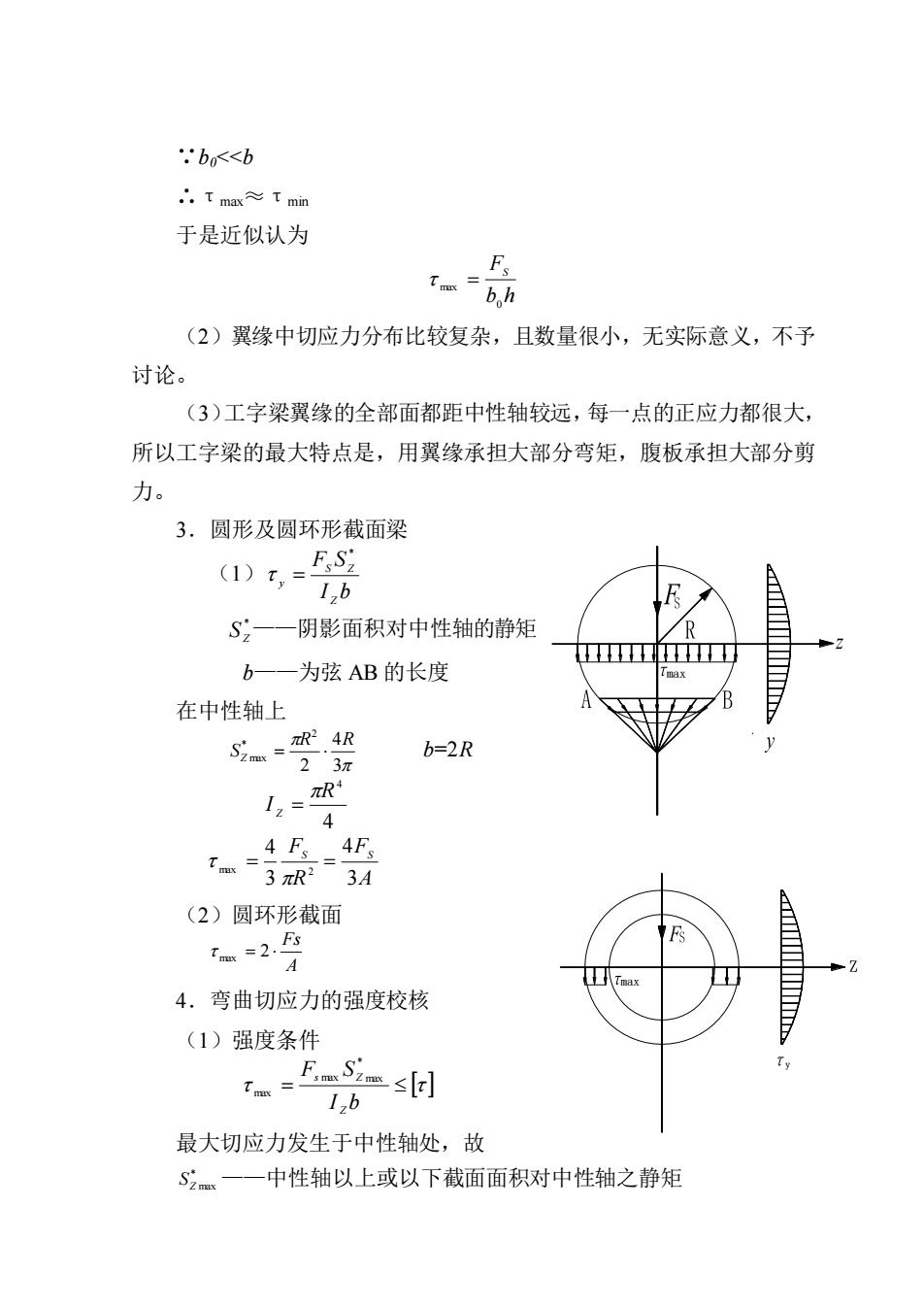
.bo<<b .Tmax≈Tmin 于是近似认为 Fs tmbh (2)翼缘中切应力分布比较复杂,且数量很小,无实际意义,不予 讨论。 (3)工字梁翼缘的全部面都距中性轴较远,每一点的正应力都很大, 所以工字梁的最大特点是,用翼缘承担大部分弯矩,腹板承担大部分剪 力。 3.圆形及圆环形截面梁 D器 S一一阴影面积对中性轴的静矩 b一一为弦AB的长度 在中性轴上 =4 b=2R 23π 4- (2)圆环形截面 2月 4.弯曲切应力的强度校核 (1)强度条件 58 最大切应力发生于中性轴处,故 S2=一一中性轴以上或以下截面面积对中性轴之静矩
∵b0<<b ∴τmax≈τmin 于是近似认为 b h FS 0 max = (2)翼缘中切应力分布比较复杂,且数量很小,无实际意义,不予 讨论。 (3)工字梁翼缘的全部面都距中性轴较远,每一点的正应力都很大, 所以工字梁的最大特点是,用翼缘承担大部分弯矩,腹板承担大部分剪 力。 3.圆形及圆环形截面梁 (1) I b F S Z S Z y * = * Z S ——阴影面积对中性轴的静矩 b——为弦 AB 的长度 在中性轴上 3 4 2 2 * max R R SZ = b=2R 4 4 R I Z = A F R FS S 3 4 3 4 max 2 = = (2)圆环形截面 A Fs = 2 max 4.弯曲切应力的强度校核 (1)强度条件 = I b F S Z s Z max * max max 最大切应力发生于中性轴处,故 * SZ max ——中性轴以上或以下截面面积对中性轴之静矩 max max y

(2)细长梁而言,强度控制因素,通常是弯曲正应力,一般只按正 应力强度条件进行强度计算,不需要对弯曲切应力进行强度校核。 (3)只在下述情况下,才进行弯曲切应力强度校核: ①梁的跨度较短。 ②在梁的支座附近作用较大的载荷,以致梁的弯矩较小,而剪力颇 大。 ③铆接或焊接的工字梁,如腹板较薄而截面高度颇大,以致厚度与 高度的比值小于型钢的相应比值,这时对腹板进行切应力校核。 ④经焊接,铆接或胶而成的梁,对焊缝、铆钉或胶合面一般进行剪 切计算。 §5.6提高弯曲强度的措施 弯曲正应力为控制梁的主要因素。由 梁的强度条件: 4 9-0125a 0s m0116111mmm、◆& 合理安排梁的受力情况,降低Mmax。 D 采用合理截面形状,提高W2 02T061021 1.合理安排梁的受力情况,降低Max M (1)合理布置梁的支座 (2)合理布置载荷 ①载荷置于合理位置 ②将集中力分为较小的集中力 22子 ③将集中力分为分布力 wamritiil2ma /2 2 4⊥ 个6↓ 51 x cimm
(2)细长梁而言,强度控制因素,通常是弯曲正应力,一般只按正 应力强度条件进行强度计算,不需要对弯曲切应力进行强度校核。 (3)只在下述情况下,才进行弯曲切应力强度校核: ①梁的跨度较短。 ②在梁的支座附近作用较大的载荷,以致梁的弯矩较小,而剪力颇 大。 ③铆接或焊接的工字梁,如腹板较薄而截面高度颇大,以致厚度与 高度的比值小于型钢的相应比值,这时对腹板进行切应力校核。 ④经焊接,铆接或胶而成的梁,对焊缝、铆钉或胶合面一般进行剪 切计算。 §5.6 提高弯曲强度的措施 弯曲正应力为控制梁的主要因素。由 梁的强度条件: = WZ M max max 合理安排梁的受力情况,降低 Mmax。 采用合理截面形状,提高 WZ 1.合理安排梁的受力情况,降低 Mmax (1)合理布置梁的支座 (2)合理布置载荷 ①载荷置于合理位置 ②将集中力分为较小的集中力 ③将集中力分为分布力