
第四章弯曲内力 §4.1弯曲的概念和实例 §4.2受弯杆件的简化 §4.3剪力和弯矩 §4.4剪力方程和弯矩方向,剪力图和弯矩图 §4.5载荷集度、剪力和弯矩间的关系 §4.6静定刚度及平面曲杆的弯曲内力 §4.1弯曲的概念和实例 1.实例 [@)桥式起重机大梁 (2)火车轮轴 (3)镗刀刀杆 (4)轧板机的轧辊 2.弯曲变形 作用于杆件上的垂直于杆件的轴线,使原为直线的轴线变形后成为 曲线,这种变形称为弯曲变形。 3.梁一一凡以弯曲变形为主的杆件,习惯上称为梁 4.对称弯曲: 「(①横截面有一根对称轴 (2)整个杆件有一个包含对称轴的纵向对称面 3)所有外力都作用于纵向对称面内 (4)弯曲变形后轴线成为纵向对称面内的一条平面曲线
第四章 弯曲内力 §4.1 弯曲的概念和实例 §4.2 受弯杆件的简化 §4.3 剪力和弯矩 §4.4 剪力方程和弯矩方向,剪力图和弯矩图 §4.5 载荷集度、剪力和弯矩间的关系 §4.6 静定刚度及平面曲杆的弯曲内力 §4.1 弯曲的概念和实例 1.实例 ( ) ( ) ( ) ( ) 轧板机的轧辊 镗刀刀杆 火车轮轴 桥式起重机大梁 4 3 2 1 2.弯曲变形 作用于杆件上的垂直于杆件的轴线,使原为直线的轴线变形后成为 曲线,这种变形称为弯曲变形。 3.梁——凡以弯曲变形为主的杆件,习惯上称为梁 4.对称弯曲: ( ) ( ) ( ) ( ) 弯曲变形后轴线成为纵向对称面内的一条平面曲线 所有外力都作用于纵向对称面内 整个杆件有一个包含对称轴的纵向对称面 横截面有一根对称轴 4 3 2 1 F 1 2
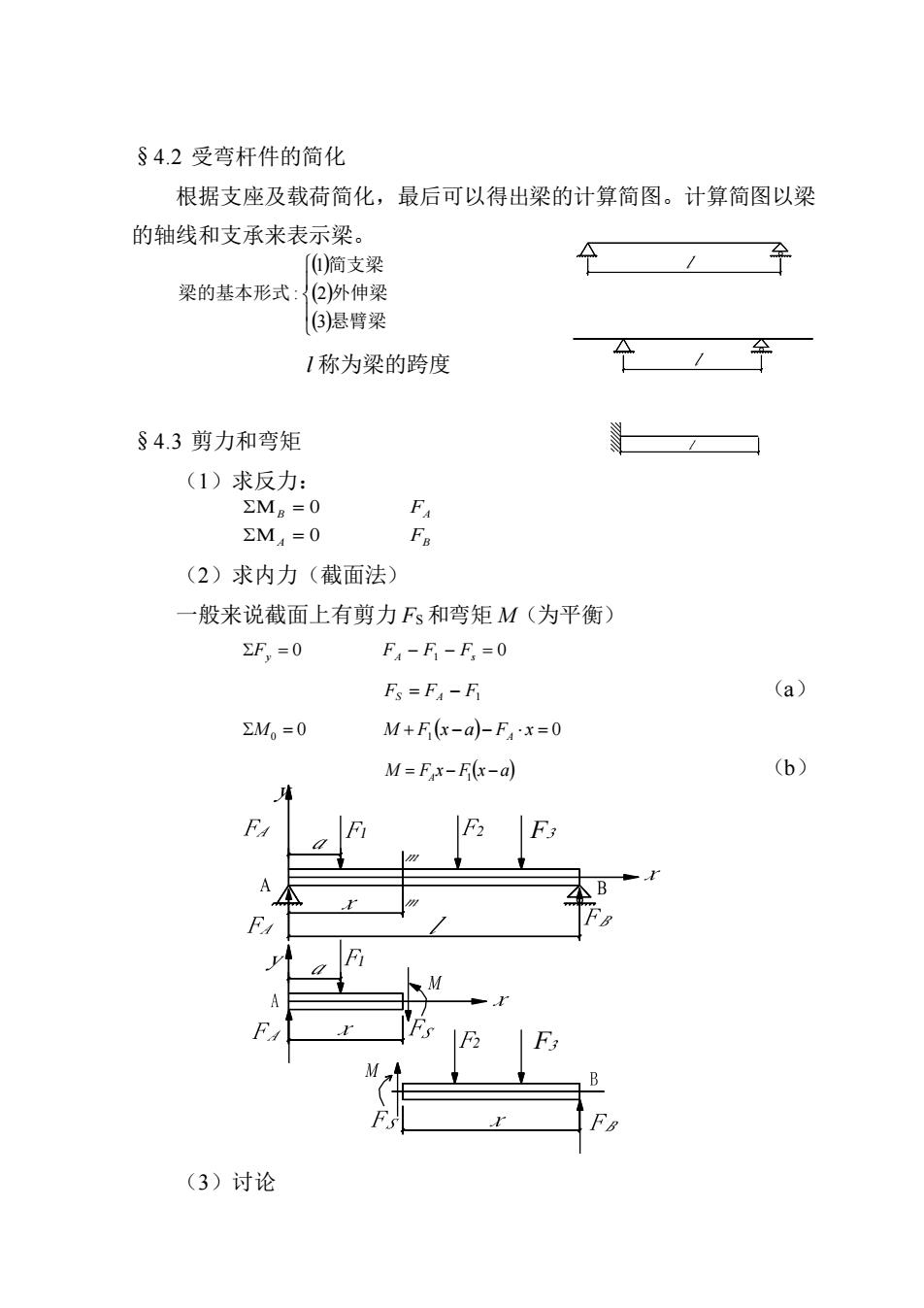
§4.2受弯杆件的简化 根据支座及载荷简化,最后可以得出梁的计算简图。计算简图以梁 的轴线和支承来表示梁。 )简支梁 梁的基本形式:2)外伸梁 3)悬臂梁 1称为梁的跨度 §4.3剪力和弯矩 (1)求反力: ΣMB=0 F M4=0 (2)求内力(截面法) 一般来说截面上有剪力Fs和弯矩M(为平衡) EF,=0 F,-F-F=0 Fs=F-F (a】 M。=0 M+F(x-a)-Fx=0 M=Fx-F(x-a) (b) F F F (3)讨论
§4.2 受弯杆件的简化 根据支座及载荷简化,最后可以得出梁的计算简图。计算简图以梁 的轴线和支承来表示梁。 ( ) ( ) ( ) 悬臂梁 外伸梁 简支梁 梁的基本形式 3 2 1 : l 称为梁的跨度 §4.3 剪力和弯矩 (1)求反力: A B B A F F 0 0 = = (2)求内力(截面法) 一般来说截面上有剪力 FS 和弯矩 M(为平衡) Fy = 0 FA − F1 − Fs = 0 FS = FA − F1 (a) 0 ( ) 0 M0 = M + F1 x − a − FA x = M F x F(x a) = A − 1 − (b) 1 2 F 1 2 F (3)讨论
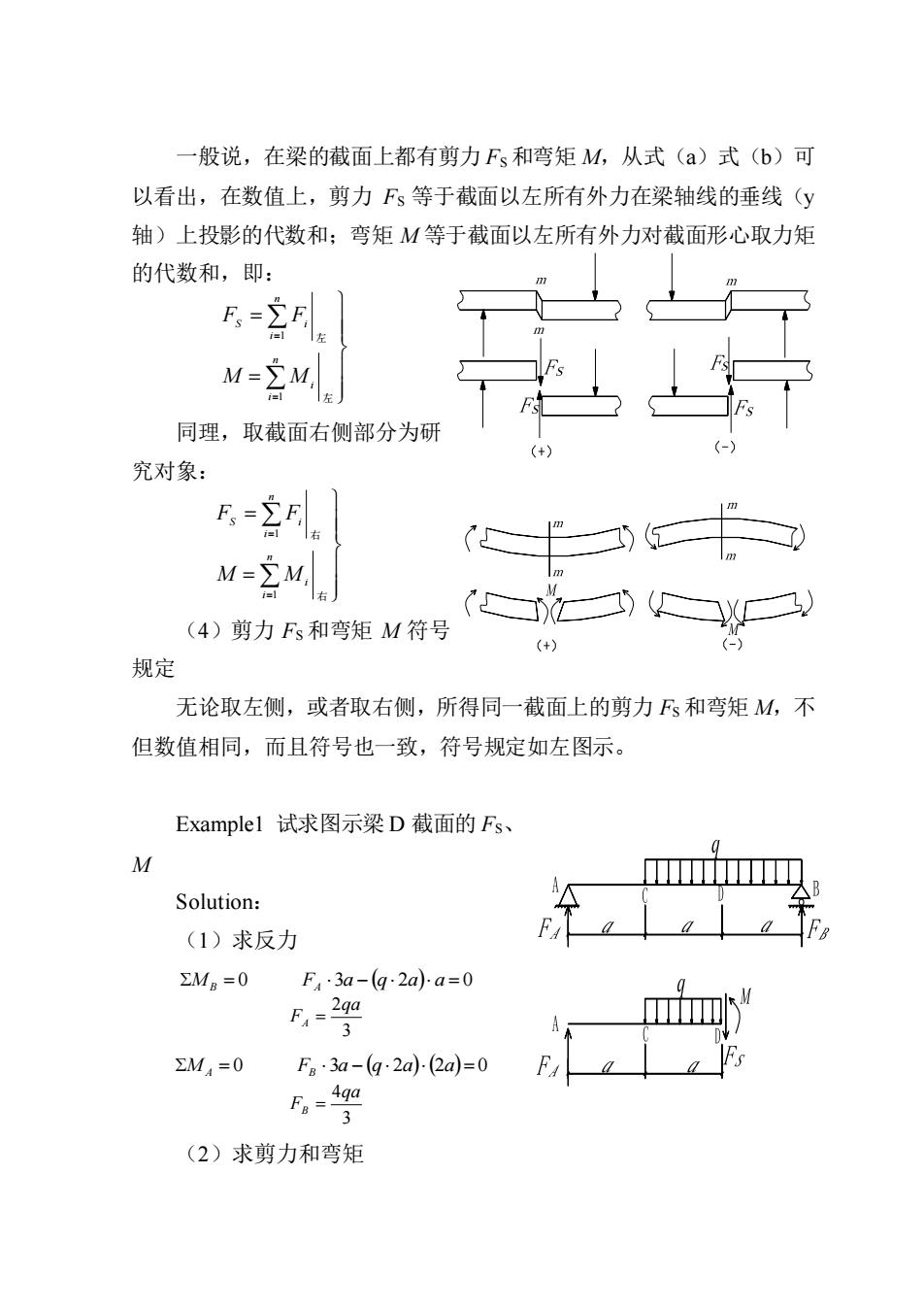
一般说,在梁的截面上都有剪力Fs和弯矩M,从式(a)式(b)可 以看出,在数值上,剪力Fs等于截面以左所有外力在梁轴线的垂线(y 轴)上投影的代数和;弯矩M等于截面以左所有外力对截面形心取力矩 的代数和,即: M=∑M, 同理,取截面右侧部分为研 究对象: F.-ZE 右 M=2M五 (4)剪力Fs和弯矩M符号 (+) (-) 规定 无论取左侧,或者取右侧,所得同一截面上的剪力Fs和弯矩M,不 但数值相同,而且符号也一致,符号规定如左图示。 Examplel试求图示梁D截面的Fs、 M I Solution: (1)求反力 Mg=0F4·3a-(g2aa=0 F-9 ΣM4=0 Fa·3a-(g-2aj-(2a)=0 (2)求剪力和弯矩
一般说,在梁的截面上都有剪力 FS 和弯矩 M,从式(a)式(b)可 以看出,在数值上,剪力 FS 等于截面以左所有外力在梁轴线的垂线(y 轴)上投影的代数和;弯矩 M 等于截面以左所有外力对截面形心取力矩 的代数和,即: = = = = 左 左 n i i n i S i M M F F 1 1 同理,取截面右侧部分为研 究对象: = = = = 右 右 n i i n i S i M M F F 1 1 (4)剪力 FS 和弯矩 M 符号 规定 无论取左侧,或者取右侧,所得同一截面上的剪力 FS 和弯矩 M,不 但数值相同,而且符号也一致,符号规定如左图示。 Example1 试求图示梁 D 截面的 FS、 M Solution: (1)求反力 MB = 0 FA 3a − (q 2a) a = 0 3 2qa FA = M A = 0 FB 3a − (q 2a)(2a)= 0 3 4qa FB = (2)求剪力和弯矩

(设正法)将截面上的剪力Fs和弯距M,按符号规定设为正的方向。 2F,=0 F4-g0-Fs=0 5=R,-909-90=-号 (负号说明剪力Fs所设方向与实际方向相反,截面上产生负剪力)。 M。=0 M-F2a+ga-0 326 (正号说所设方向与实际方向一致,截面上产生正弯矩)。 Exemple22试求图示梁1-l,2-2截 面上的剪力和弯矩 F Solution: ①求反力: 2MB=0 F1-Fb=0 F.- EM,=0 Fs1-Fa=0 ②求剪力和弯矩,1-1截面 F=0 F-Fs=0 EM。=0 M,-F4·a=0 M,-F,a=Fba 2-2截面 F,=0 F4-F-F2=0 =R,-F=中-F- (负号说明剪力方向与实际方向相反,在截面上剪力为负值) M。=0 M2-F4·a=0
(设正法)将截面上的剪力 FS 和弯距 M,按符号规定设为正的方向。 Fy = 0 FA − qa − FS = 0 3 3 2 qa qa qa FS = FA − qa = − = − (负号说明剪力 FS 所设方向与实际方向相反,截面上产生负剪力)。 0 2 = 0 − 2 + = a M D M FA a qa 6 5 3 2 4 2 2 2 2 2 2 2 qa qa qa qa M = FA a − = − = (正号说所设方向与实际方向一致,截面上产生正弯矩)。 Exemple2 试求图示梁 1-1,2-2 截 面上的剪力和弯矩 Solution: ①求反力: MB = 0 FA l − Fb = 0 l Fb FA = M A = 0 FB l − Fa = 0 l Fa FB = ②求剪力和弯矩,1-1 截面 Fy = 0 FA − FS1 = 0 l Fba M1 = FA a = 2-2 截面 Fy = 0 FA − F − FS 2 = 0 l Fa F l Fb FS 2 = FA − F = − = − (负号说明剪力方向与实际方向相反,在截面上剪力为负值) M0 = 0 M2 − FA a = 0 M0 = 0 M1 − FA a = 0 2 1 2 1 1 1 o o 2 2 F 2

站-Ra Example3试求图示梁1-1、2-2截面上的剪力和弯矩 Solution ①求反力: 2MB=0 F41-M.=0 F EM=0 FBI+M。=0 (负号说明,所设反力方向与实际 方向相反) ②求剪力和弯矩 1-1截面:设Fs1,M F=0 F4-F1=0 F=5,= M。=0 F4a-M1=0 M-a-a 2-2截面:设Fs2,M(设正法) F.=0 Fs2+FB=0 5=-f=4 ΣM。=0 M2-FB·b=0 站-月6-华b (所设方向与实际方向相反,为负弯矩) Example4试求梁1-1、2-2截面上的剪力和弯矩 Solution::根据前面剪力和弯矩的求代数和的规则来求剪力和弯矩
l Fba M 2 = FA a = Example3 试求图示梁 1-1、2-2 截面上的剪力和弯矩 Solution ①求反力: M B = 0 FA l − Me = 0 l M F e A = M A = 0 FB l + Me = 0 l M F e B = − (负号说明,所设反力方向与实际 方向相反) ②求剪力和弯矩 1-1 截面:设 FS1,M1 Fy = 0 FA − FS1 = 0 l M F F e S1 = A = M0 = 0 FA a − M1 = 0 a l Me M1 = FA a = 2-2 截面:设 FS2,M2(设正法) Fy = 0 FS 2 + FB = 0 l M F F e S 2 = − B = M0 = 0 M2 − FB b = 0 b l Me M2 = FB b = − (所设方向与实际方向相反,为负弯矩) Example4 试求梁 1-1、2-2 截面上的剪力和弯矩 Solution:根据前面剪力和弯矩的求代数和的规则来求剪力和弯矩。 1 1 2 2 o o 1 1 o 2 2 2

Me-ga F=qa A a a 1-1截面: Fs=-qa 2-2截面: Fs2=-qa-qa=-2ga a 22 Example5:试求梁1-l、2-2截面上的剪力和弯矩 Solution:(取右侧) Me=ga q F=ga A 2i 2d1 a a 1-1截面: Fs=F+qa=qa+qa=2qa M=ga-a-g0号=390 3 2-2截面: Fs2=2qa Γ2 §4.4剪力方程和弯矩方向,剪力图和弯矩图 1.一般情况下,梁横截面上的剪力和弯矩随截面位置不同而变化
2 2 1 1 a a Me= 1-1 截面: 2 2 2 2 2 2 1 1 qa qa qa a M M qa F qa e S = − = = − = − 2-2 截面: 2 2 2 2 2 2 2 2 2 qa qa qa a M M qa F qa qa qa e S = − = = − = − − = − Example5 试求梁 1-1、2-2 截面上的剪力和弯矩 Solution:(取右侧) 1 c 1 2 2 a a Me= 1-1 截面: 2 1 1 2 3 2 2 qa a M qa a qa FS F qa qa qa qa = − − = − = + = + = 2-2 截面: 2 2 2 2 2 2 2 qa qa a M qa a qa FS qa = − − + = − = §4.4 剪力方程和弯矩方向,剪力图和弯矩图 1.一般情况下,梁横截面上的剪力和弯矩随截面位置不同而变化

剪力和弯矩为截面位置坐标x的函数。 F=F() 左上 正剪力④ M=M(x) 上面函数表达式称为剪力方程和弯矩方程,根 负剪力⊙ 据剪力方程和弯矩方程,可以描出剪力和弯矩随截 面位置变化规律的图线称为剪力图和弯矩图。 乙左上)正弯距⊕ 2.列剪力方程和弯矩方程规则 左下 负弯距 5-2 e M-M 左☐)正弯距① (1)截面左侧向上的外力都在剪力代数和式 中取正号,向下的外力都取负号。(左上取正,右■ ■)负弯距 下为负) (2)截面左侧向上的外力对截面形心产生的力矩都在弯矩代数和式 中取正号。向下的外力对截面形心所在产生的力矩都在和式中取负号。 (3)截面左侧顺时针转的外力偶矩,在力矩总和式中取正号,负之 取负号(顺正、逆负) E=2 ⊕正剪力右下了 M-M. ⊙负剪力右上了 个 (1)截面右侧梁上向下的外力在剪力代数和⑧正弯距(右上了 式中取正号,向上的外力取负号。 (2)截面左侧梁上向上的外力在弯矩代数和 ⊙负弯距(右下了 式中取正号,向下的外力之力矩取负号。 (3)截面右侧梁上逆时针外力偶矩在弯矩代®正弯距(型包 数和式中取正号,顺取负号。 Me ⊙负弯距(顺了
剪力和弯矩为截面位置坐标 x 的函数。 ( ) ( ) = = M M x F F x S S 上面函数表达式称为剪力方程和弯矩方程,根 据剪力方程和弯矩方程,可以描出剪力和弯矩随截 面位置变化规律的图线称为剪力图和弯矩图。 2.列剪力方程和弯矩方程规则 = = = = 左 左 n i i n i S i M M F F 1 1 (1)截面左侧向上的外力都在剪力代数和式 中取正号,向下的外力都取负号。(左上取正,右 下为负) (2)截面左侧向上的外力对截面形心产生的力矩都在弯矩代数和式 中取正号。向下的外力对截面形心所在产生的力矩都在和式中取负号。 (3)截面左侧顺时针转的外力偶矩,在力矩总和式中取正号,负之 取负号(顺正、逆负) = = = = 右 右 n i i n i S i M M F F 1 1 (1)截面右侧梁上向下的外力在剪力代数和 式中取正号,向上的外力取负号。 (2)截面左侧梁上向上的外力在弯矩代数和 式中取正号,向下的外力之力矩取负号。 (3)截面右侧梁上逆时针外力偶矩在弯矩代 数和式中取正号,顺取负号。 左上 正剪力 左下 负剪力 左下 负弯距 左上 正弯距 左逆 左顺 负弯距 正弯距 e e 负剪力 右上 正剪力 右下 负弯距 正弯距 右上 右下 右逆 负弯距 右顺 正弯距 e e

Examplel试作梁的梁剪力图和弯矩图 Solution ①求反力 L Fu =9l ②列方程 6-0-号-mo<a<刘 m. M6)=Fx-gx=x-9四0≤x≤) 22 2 ③绘图 am→ Fx)为x的一次函数斜直线,确定一点。 当=0时, E()=9 2 当=1时, F)=- 2 M(x)为x的二次函数,是一抛物线,定数点 当=0时, M(x)=0 当x=时, M)=3 9/ 当x=号时, M)=9t 8 当时 ( 当=时, M(x)=0 ④rL=婴 山=gE 8 Example2镗刀杆的计算简图,试作Fs、 M图 Solution: ,Ilmm
Example1 试作梁的梁剪力图和弯矩图 Solution ①求反力 2 ql FRA = 2 ql FRB = ②列方程 ( ) (0 1) 2 = − = − qx x ql F x F qx S RA ( ) ( x l) qx x x ql M x F x qx = RA − = − 0 2 2 2 2 ③绘图 F(x)为 x 的一次函数斜直线,确定一点。 当 x=0 时, ( ) 2 ql F x s = 当 x=l 时, ( ) 2 ql F x s = − M(x)为 x 的二次函数,是一抛物线,定数点 当 x=0 时, M(x)=0 当 4 l x = 时, ( ) 2 32 3 M x = ql 当 2 l x = 时, ( ) 8 2 ql M x = 当 4 3l x = 时, ( ) 2 32 3 M x = ql 当 x=l 时, M(x)=0 ④ , 2 max ql FS = 8 2 max ql M = Example2 镗刀杆的计算简图,试作 FS、 M 图 Solution: + - + 2 8 2 x l RA RB M x x ql ql ql x l S S

①可以求反力,也可以不求反力 ②列方程 Fs(x)=F (0<xK) M(x)=-F(1-x) (0<x≤D ③绘图 Fsx)为常数,为水平线 Mx)为x的一次函数,斜直线,定二点 当=0时 M(x)=-FI 当=1时 M(x)=0 ④Fsmax=f M=FI Example3.齿轮轴计算简图,作Fs、M图 Solution ①求反力 EMg=0 F41-Fb=0 M,=0 Fpl-Fa=0 R-只 Eb 皿 ②列Fs、M方程,集中力F作用,分段 → 列方程 C)FG)=R,-色 (0<x1<a) am M)-E,-中0≤X≤a (CB)a,)E-F=-F=-只 (0<x2<) 1 M6=5%-P6-d=5-Pk-0)(0≤a≤0 ③绘图 (AC))乃常数为水平线
①可以求反力,也可以不求反力 ②列方程 FS(x)=F (0<x<l) M(x)=-F(l-x) (0<x≤l) ③绘图 FS(x)为常数,为水平线 M(x)为 x 的一次函数,斜直线,定二点 当 x=0 时 M(x)=-Fl 当 x=l 时 M(x)=0 ④ FSmax=F M = Fl max Example3 齿轮轴计算简图,作 FS、M 图 Solution ①求反力 l Fb M B = 0 FA l − Fb = 0 FA = l Fa M A = 0 FB l − Fa = 0 FB = ②列 FS、M 方程,集中力 F 作用,分段 列方程 (AC ) ( ) l Fb FS1 x1 = FA = (0<x1<a) ( ) 1 1 1 1 x l Fb M x F x = A = (0≤x1≤a) ( CB ) ( ) l Fa F l Fb FS 2 x2 = FA − F = − = − (0<x2<l) ( ) ( ) x F(x a) l Fb M2 x2 = FA x2 − F x2 − a = 2 − 2 − (0≤x2≤l) ③绘图 (AC) ( ) l Fb F x S1 1 = 常数为水平线 + - Fb l l Fa Fab + x l b l

M(x)为x1的一次函数,斜直线,定=点 当x=0时,M(x)=0 当=a时,M()=Fba (CB)E.k)-为水平 M(2)为x的一次函数,斜直线,定=点 当=a时,M(n)=Fba 当x2=1时,4(x32)=0 ④ E=a9到 M=pab 1 Example4试作Fs、M图 Solution ①求反力 EM2=0 F41+M。=0 EM4=0 Fal-M。=0 ②列方程,分段列方程 u (AC)F)F (0<x≤a) M)R,=40≤X (CB)5a)R=-¥ (a≤x2<) M22)=Fx2+M。=- 4x+M.(a<X≤D ③绘图 F,八常数、水平线 F,x2月
M1(x1)为 x1的一次函数,斜直线,定=点 当 x1=0 时,M1(x1)=0 当 x1=a 时,M1(x1)= l Fba (CB) ( ) l Fa F x S 2 2 = − 为水平 M2(x2)为 x 的一次函数,斜直线,定=点 当 x2=a 时,M2(x2)= l Fba 当 x2=l 时,M2(x2)=0 ④ ( ) l pab M a b l Fa Fs = = max max 若 Example4 试作 FS、M 图 Solution ①求反力 l M M F l M F e B = 0 A + e = 0 A = l M M F l M F e A = 0 B − e = 0 B = ②列方程,分段列方程 (AC) ( ) l M F x F e S1 1 = A = − (0<x1≤a) ( ) 1 1 1 1 x l M M x F x e = A = (0≤x1<a) (CB) ( ) l M F x F e S 2 2 = A = − (a≤x2<l) ( ) e e A e x M l M M2 x2 = F x2 + M = − 2 + (a<x2≤l) ③绘图 ( ) ( ) 2 2 1 1 F x F x S S 常数、水平线 C l - Me l - + a Me l b a b x l x Me