
第二章拉伸、压缩与剪切 §2.1轴向拉伸与压缩的概念和实例 §2.2轴向拉伸或压缩时横截面上的内力和应力 §2.3直杆轴向拉伸或压缩时斜截面上的应力 §2.4材料拉伸时的力学性能 §2.5材料压缩时的力学性能 §2.7失效、安全因数和强度计算 §2.8轴向拉伸或压缩时的变形 §2.9轴向拉伸或压缩的应变能 §2.10拉伸、压缩超静定问题 §2.11温度应力和装配应力 §2.12应力集中的概念 §2.13剪切和挤压的实用计算 §2.1轴向拉伸与压缩的概念和实例 1.实例 (1)液压传动中的活塞杆 (2)内燃机的连杆 (3)汽缸的联接螺栓 (4)起吊重物用的钢索 (5)千斤顶的螺杆 (6)桁架的杆件
第二章拉伸、压缩与剪切 §2.1 轴向拉伸与压缩的概念和实例 §2.2 轴向拉伸或压缩时横截面上的内力和应力 §2.3 直杆轴向拉伸或压缩时斜截面上的应力 §2.4 材料拉伸时的力学性能 §2.5 材料压缩时的力学性能 §2.7 失效、安全因数和强度计算 §2.8 轴向拉伸或压缩时的变形 §2.9 轴向拉伸或压缩的应变能 §2.10 拉伸、压缩超静定问题 §2.11 温度应力和装配应力 §2.12 应力集中的概念 §2.13 剪切和挤压的实用计算 §2.1 轴向拉伸与压缩的概念和实例 1.实例 (1)液压传动中的活塞杆 (2)内燃机的连杆 (3)汽缸的联接螺栓 (4)起吊重物用的钢索 (5)千斤顶的螺杆 (6)桁架的杆件
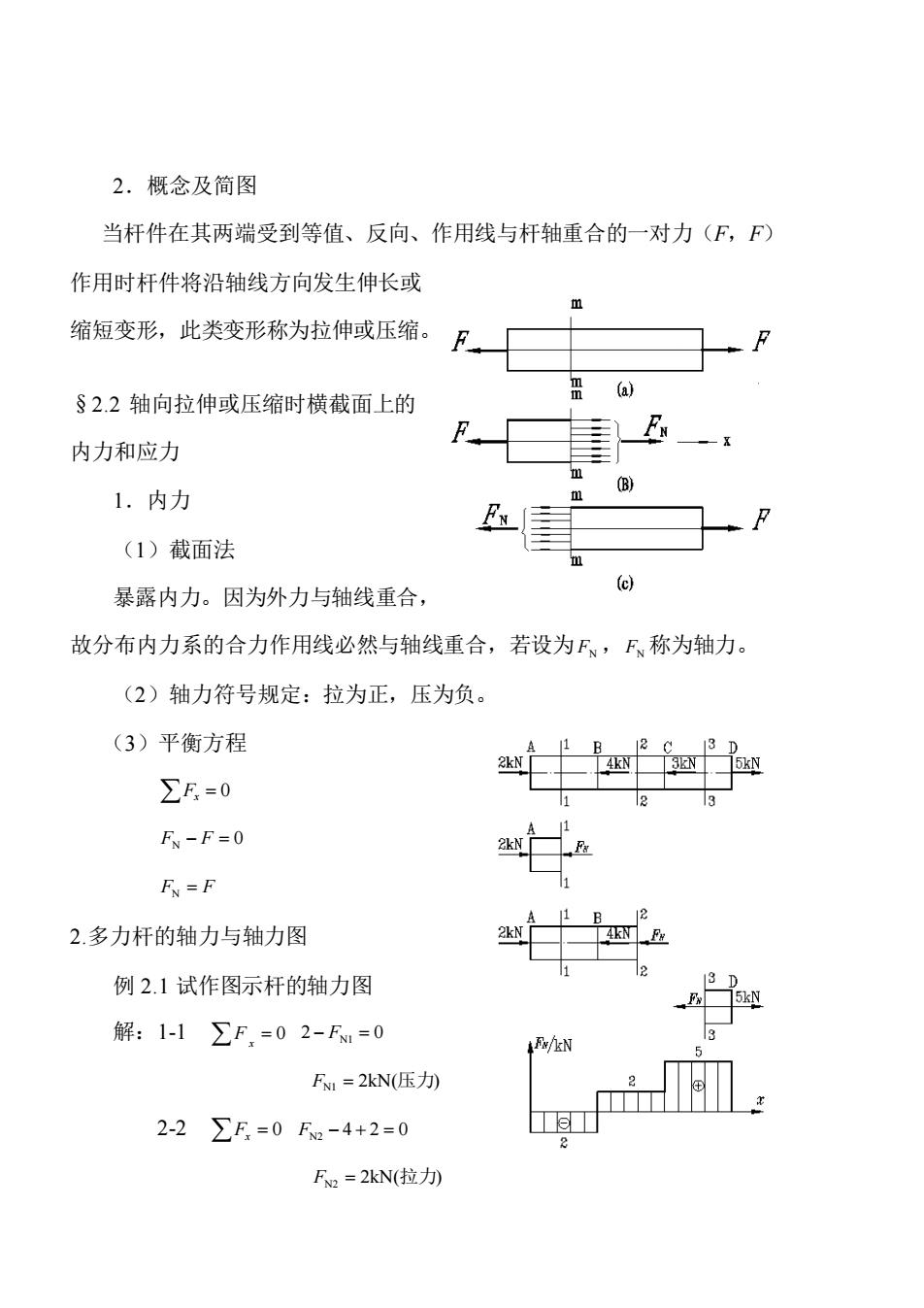
2.概念及简图 当杆件在其两端受到等值、反向、作用线与杆轴重合的一对力(F,F) 作用时杆件将沿轴线方向发生伸长或 缩短变形,此类变形称为拉伸或压缩。 (a) §2.2轴向拉伸或压缩时横截面上的 内力和应力 1.内力 (1)截面法 暴露内力。因为外力与轴线重合, 故分布内力系的合力作用线必然与轴线重合,若设为F,F称为轴力。 (2)轴力符号规定:拉为正,压为负。 (3)平衡方程 1 R 2013D ∑F=0 23 F-F=0 F=F 2.多力杆的轴力与轴力图 例2.1试作图示杆的轴力图 解:1-1∑F,=02-F=0 F1=2kN压) 2-2∑F=0Fa-4+2=0 F2=2kN(拉力
2.概念及简图 当杆件在其两端受到等值、反向、作用线与杆轴重合的一对力(F,F) 作用时杆件将沿轴线方向发生伸长或 缩短变形,此类变形称为拉伸或压缩。 §2.2 轴向拉伸或压缩时横截面上的 内力和应力 1.内力 (1)截面法 暴露内力。因为外力与轴线重合, 故分布内力系的合力作用线必然与轴线重合,若设为 FN ,FN 称为轴力。 (2)轴力符号规定:拉为正,压为负。 (3)平衡方程 Fx = 0 FN − F = 0 FN = F 2.多力杆的轴力与轴力图 例 2.1 试作图示杆的轴力图 解:1-1 = 0 x F 2 − FN1 = 0 2kN( ) FN1 = 压力 2-2 Fx = 0 FN2 − 4 + 2 = 0 2kN( ) FN2 = 拉力
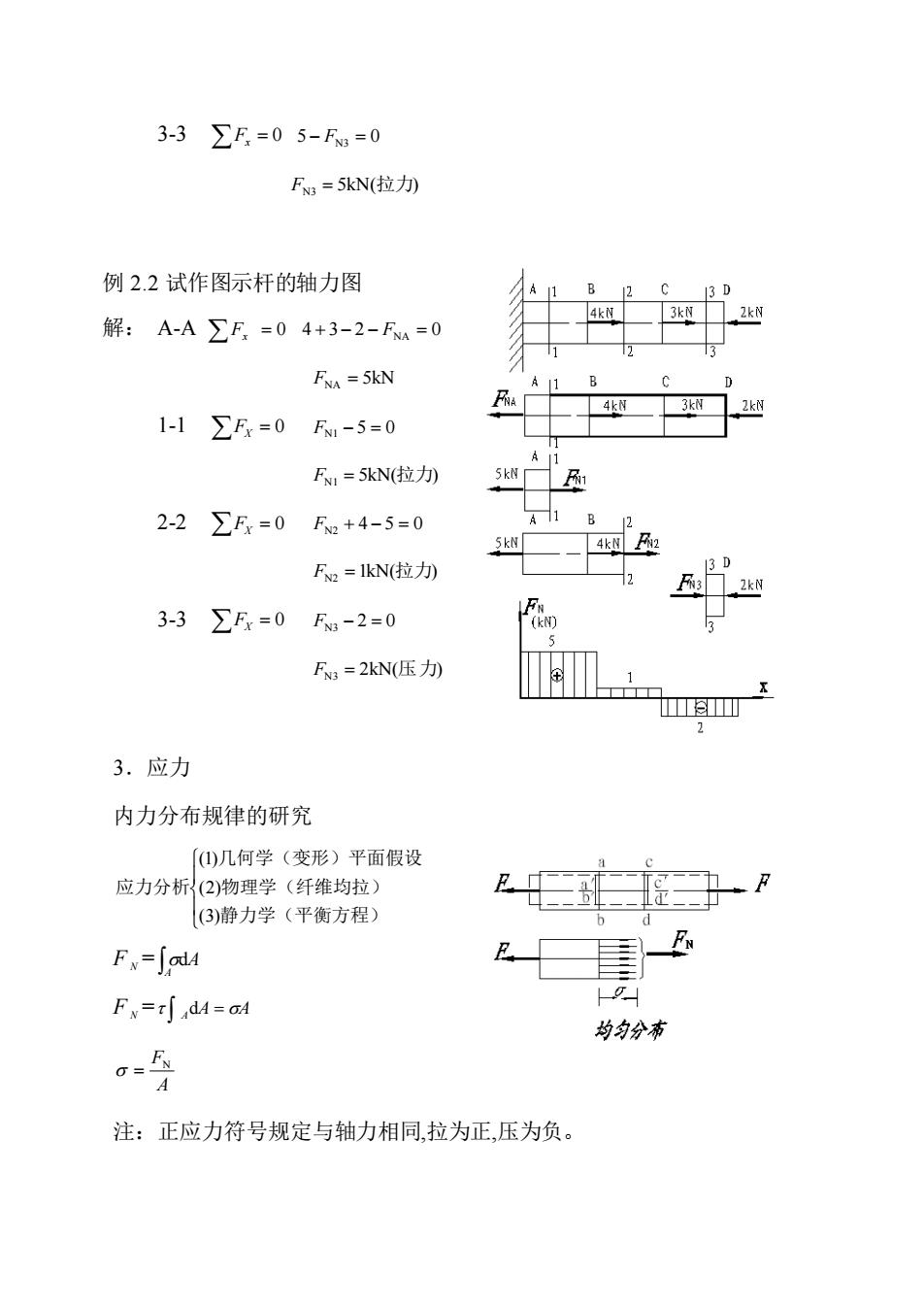
3-3∑F=05-R=0 F=5kN(拉 例2.2试作图示杆的轴力图 解:A-A∑F,=04+3-2-F=0 FNA 5kN RA 1-1∑Fx=0F1-5=0 FN,=5kN(拉) 5kNi 2-2∑Fx=0F2+4-5=0 B Fa=IkN(拉) 2kN 3-3∑F=0F-2=0 F=2N(压九 3.应力 内力分布规律的研究 [仙)几何学(变形)平面假设 应力分析(2)物理学(纤维均拉) (3)静力学(平衡方程) Fx-∫aM Fx=rdA=aA 均的分布 注:正应力符号规定与轴力相同,拉为正,压为负
3-3 Fx = 0 5 − FN3 = 0 5kN( ) FN3 = 拉力 例 2.2 试作图示杆的轴力图 解: A-A Fx = 0 4 + 3− 2 − FNA = 0 FNA = 5kN 1-1 FX = 0 FN1 − 5 = 0 5kN( ) FN1 = 拉力 2-2 FX = 0 FN2 + 4 − 5 = 0 1kN( ) FN2 = 拉力 3-3 FX = 0 FN3 − 2 = 0 2kN( ) FN3 = 压力 3.应力 内力分布规律的研究 静力学(平衡方程) 物理学(纤维均拉) 几何学(变形)平面假设 应力分析 (3) (2) (1) F N = A dA F N = A A = A d A F = 注:正应力符号规定与轴力相同,拉为正,压为负
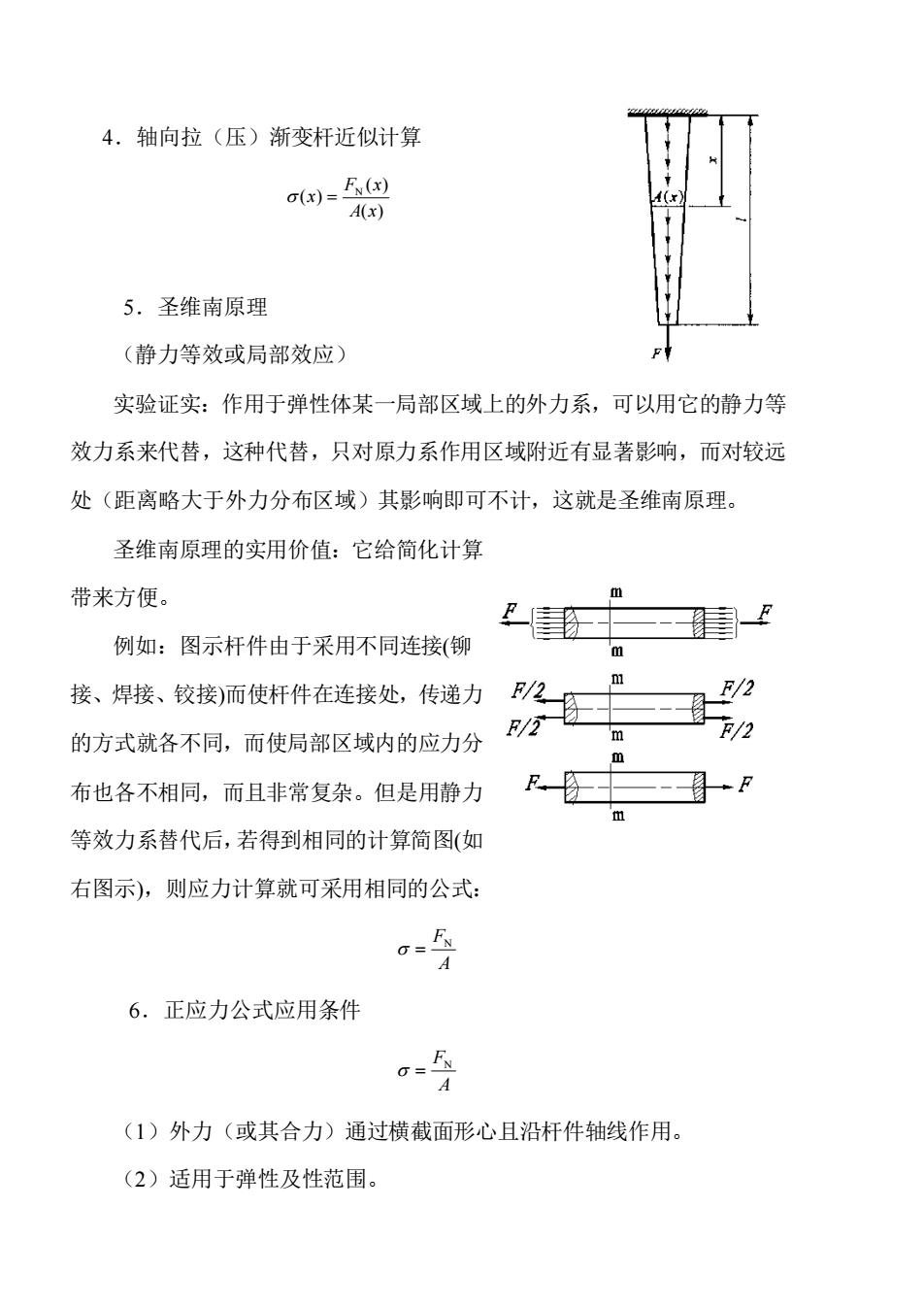
4.轴向拉(压)渐变杆近似计算 ()= A(x) 5.圣维南原理 (静力等效或局部效应) 实验证实:作用于弹性体某一局部区域上的外力系,可以用它的静力等 效力系来代替,这种代替,只对原力系作用区域附近有显著影响,而对较远 处(距离略大于外力分布区域)其影响即可不计,这就是圣维南原理。 圣维南原理的实用价值:它给简化计算 带来方便。 例如:图示杆件由于采用不同连接(铆 m F/2 m 接、焊接、铰接)而使杆件在连接处,传递力 F/2 F/2 的方式就各不同,而使局部区域内的应力分 m F/2 布也各不相同,而且非常复杂。但是用静力 等效力系替代后,若得到相同的计算简图(如 右图示),则应力计算就可采用相同的公式: A 6.正应力公式应用条件 = A (1)外力(或其合力)通过横截面形心且沿杆件轴线作用。 (2)适用于弹性及性范围
4.轴向拉(压)渐变杆近似计算 ( ) ( ) ( ) A x F x x = 5.圣维南原理 (静力等效或局部效应) 实验证实:作用于弹性体某一局部区域上的外力系,可以用它的静力等 效力系来代替,这种代替,只对原力系作用区域附近有显著影响,而对较远 处(距离略大于外力分布区域)其影响即可不计,这就是圣维南原理。 圣维南原理的实用价值:它给简化计算 带来方便。 例如:图示杆件由于采用不同连接(铆 接、焊接、铰接)而使杆件在连接处,传递力 的方式就各不同,而使局部区域内的应力分 布也各不相同,而且非常复杂。但是用静力 等效力系替代后,若得到相同的计算简图(如 右图示),则应力计算就可采用相同的公式: A F = 6.正应力公式应用条件 A F = (1)外力(或其合力)通过横截面形心且沿杆件轴线作用。 (2)适用于弹性及性范围
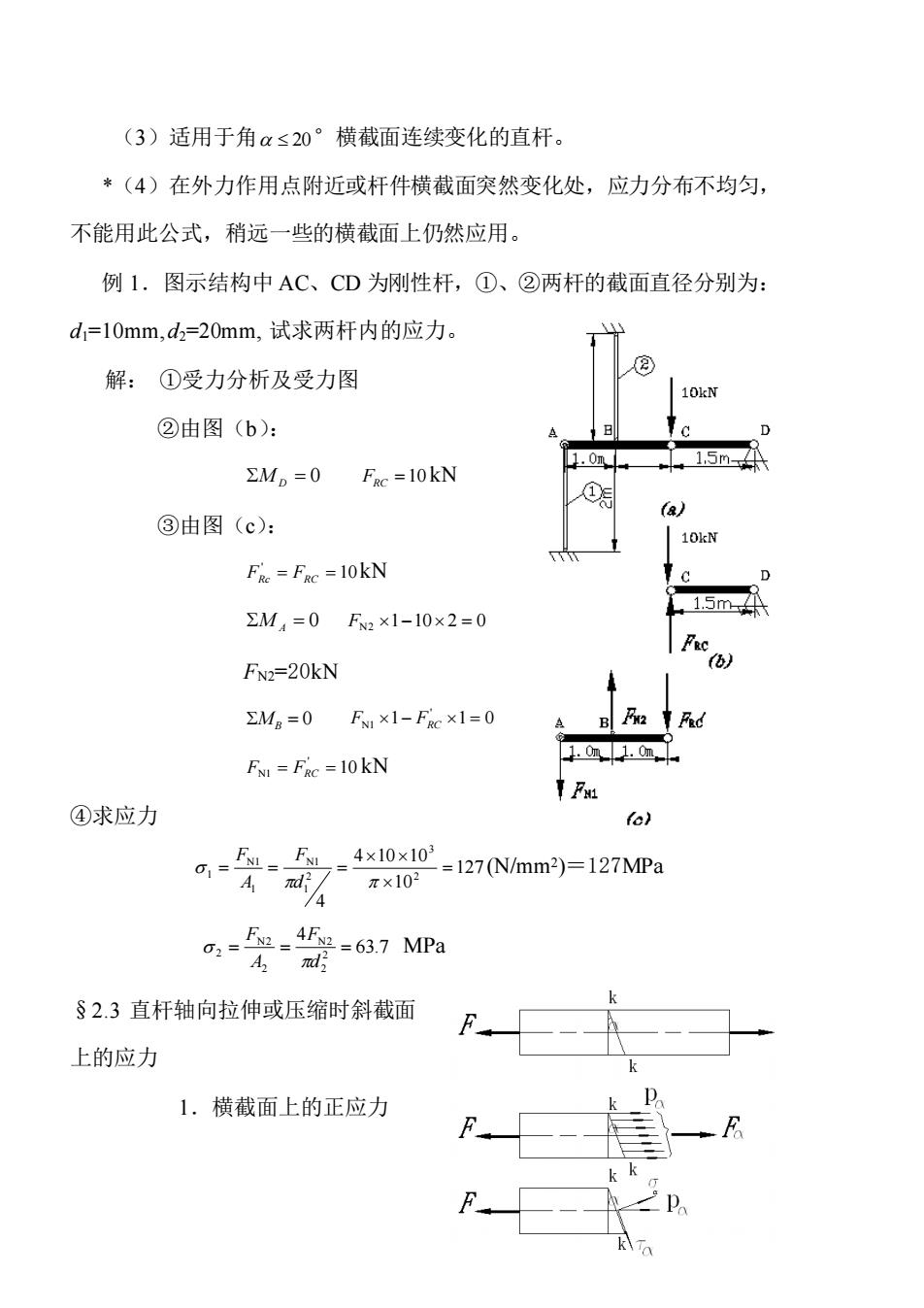
(3)适用于角α≤20°横截面连续变化的直杆。 *(4)在外力作用点附近或杆件横截面突然变化处,应力分布不均匀, 不能用此公式,稍远一些的横截面上仍然应用。 例1.图示结构中AC、CD为刚性杆,①、②两杆的截面直径分别为: d1=10mm,d2=20mm,试求两杆内的应力。 解:①受力分析及受力图 OkN ②由图(b): ΣMD=0Fac=I0kN 2.0+ 15m a ③由图(c): FRe Fgc =10kN 1.5m= EM4=0F2×1-10×2=0 FN2=20kN ∑Ma=0FN×1-Fc×1=0 FN FRc =10kN ④求应力 c 6,-型=7于40a-127Nmm29-127MPa π×102 §2.3直杆轴向拉伸或压缩时斜截面 F■ 上的应力 1.横截面上的正应力
(3)适用于角 20 °横截面连续变化的直杆。 *(4)在外力作用点附近或杆件横截面突然变化处,应力分布不均匀, 不能用此公式,稍远一些的横截面上仍然应用。 例 1.图示结构中 AC、CD 为刚性杆,①、②两杆的截面直径分别为: d1=10mm, d2=20mm, 试求两杆内的应力。 解: ①受力分析及受力图 ②由图(b): M D = 0 FRC =10 kN ③由图(c): 10 ' FRc = FRC = kN M A = 0 F2 1−10 2 = 0 FN2=20kN MB = 0 1 1 0 ' F1 − FRC = 10 ' F1 = FRC = kN ④求应力 127 10 4 10 10 4 2 3 2 1 1 1 1 1 = = = = d F A F (N/mm2 )=127MPa 63.7 4 2 2 2 2 2 2 = = = d F A F MPa §2.3 直杆轴向拉伸或压缩时斜截面 上的应力 1.横截面上的正应力

号 2.斜截面上的应力 F=F A.= A-气=无背mu=dcma =Pa cosa=a cosia t-p,smn a-gcosa.sin a-3sn 2a 讨论 (1)ō。、t.均为α的函数,随斜截面的方向而变化。 (2)当a=0°时,o.m=c、t。=0横截面上。 当a=45°时,m=号、o,=号 当a=90°时,o。=t。=0平行于轴线纵截面。 §2.4材料拉伸时的力学性能 材料在外力作用下表现出变形及破坏的特性。材料的宏观力学性能主要 依靠实验方法测定。如材料的比例极限σ,弹性极限。,屈服极限。,延伸 率6,断面收缩率中,弹性模量E,横向变形因数(泊松比)μ等。 载荷静载 动载 试验 常温 温度高度 低温
A F = 2.斜截面上的应力 F = F cos A A = = = = cos = cos A F A F A F p = = = = = sin 2 2 sin cos sin cos cos2 pa p 讨论 (1) 、 均为 的函数,随斜截面的方向而变化。 (2)当 = 0 °时, max = 、 = 0 横截面上。 当 = 45 °时, 2 max = 、 2 = 当 = 90 °时, = = 0 平行于轴线纵截面。 §2.4 材料拉伸时的力学性能 材料在外力作用下表现出变形及破坏的特性。材料的宏观力学性能主要 依靠实验方法测定。如材料的比例极限 p ,弹性极限 e ,屈服极限 s ,延伸 率 ,断面收缩率ψ,弹性模量 E,横向变形因数(泊松比)μ等。 低温 高度 常温 温度 动载 静载 载荷 试验

常温、静载下拉伸试验是确立材料力学性能的最基本试验。 试验设备:万能材料试验机。 圆截面:1=5d域1=10d 04125 标准试件矩型截面:1=5.65√A或 1=11.3A 以低碳钢(含碳量低于0.3%的碳素钢) 为例介绍拉伸试验。 一、低碳钢(Q235)拉伸时的力学性能 (1)夹持试件 (2)油压缓慢加载使试件受拉 (3)记录F~△L测试数值 (4)直至拉断,观察力与变形的全过程 (5)绘制F~△L拉伸曲线(自动绘图) (6)清除尺寸影响作o~ε曲线,根据曲 线特征大致分为四个阶段研究材料力学性能。 1.弹性阶段(Ob) 此阶段的变形为弹性变形 [(oa)直线段c。一比例极限 当c≤o时 o=Ee(胡克定律) ob E=。=ana弹性模量E,比例常数线弹性) (ab)非直线段(非线弹性) O。_弹性极限
常温、静载下拉伸试验是确立材料力学性能的最基本试验。 试验设备:万能材料试验机。 标准试件 = = = = l A l A l d l d 11.3 5.65 5 10 矩型截面: 或 圆截面: 或 以低碳钢(含碳量低于 0.3%的碳素钢) 为例介绍拉伸试验。 一、低碳钢(Q235)拉伸时的力学性能 (1)夹持试件 (2)油压缓慢加载使试件受拉 (3)记录 F~ΔL 测试数值 (4)直至拉断,观察力与变形的全过程 (5)绘制 F~ΔL 拉伸曲线(自动绘图) (6)清除尺寸影响作σ~ε曲线,根据曲 线特征大致分为四个阶段研究材料力学性能。 1.弹性阶段(Ob) 此阶段的变形为弹性变形 ( ) = = = 弹性极限 ( )非直线段 非线弹性 弹性模量 比例常数(线弹性) (胡克定律) 当 时 直线段 —比例极限 _ ab ( ) tan , (oa) ob e p p E E E

2.屈服阶段(bc) 屈服现象:当应力超过b点后,应力先 是下降后是微小波动,曲线出现接近水平 线小锯齿形线段。即应力不再增加,但应变显著增加,此现象称为屈服。 *观察测力度盘指针停走或后退。 *观察试件表面可见大致与轴线成45°方向上有细线,称为滑移线。因 为45°方向上剪应力最大。材料内部晶格沿45°方向滑动: *σ。一一屈服极限。(下屈服点) *屈服阶段主要产生塑性变形。 *屈服极限为重要的强度指标。 3.强化阶段(ce) *材料抵抗变形的能力又继续增加,即随着试件继续变形,外力也必须 增大,此现象称为材料强化。 *·。一一强度极限,发生断裂时的应力 4.局部变形阶段(颈缩)(ef) 试件局部范围横向尺寸急剧缩小,称为颈缩。 5.延伸率和断面收缩率 试件拉断后,弹性变形消失,而塑性变形保留下来。 延伸率: 6-4-'x100% 6,=4x10%=6(塑性应变)
2.屈服阶段(bc) 屈服现象:当应力超过 b 点后,应力先 是下降后是微小波动,曲线出现接近水平 线小锯齿形线段。即应力不再增加,但应变显著增加,此现象称为屈服。 * 观察测力度盘指针停走或后退。 * 观察试件表面可见大致与轴线成 45°方向上有细线,称为滑移线。因 为 45°方向上剪应力最大。材料内部晶格沿 45°方向滑动。 * σs——屈服极限。(下屈服点) * 屈服阶段主要产生塑性变形。 * 屈服极限为重要的强度指标。 3.强化阶段(ce) * 材料抵抗变形的能力又继续增加,即随着试件继续变形,外力也必须 增大,此现象称为材料强化。 *σb——强度极限,发生断裂时的应力 4.局部变形阶段(颈缩)(ef) 试件局部范围横向尺寸急剧缩小,称为颈缩。 5.延伸率和断面收缩率 试件拉断后,弹性变形消失,而塑性变形保留下来。 延伸率: 100% 1 − = l l l = = 100% l l (塑性应变)

【一一原标距 1一一拉断后标距长度 塑性指标: 8>5%— 一塑性材料,钢、铜、铝 6<5%一一脆性材料,铸铁、玻璃、陶瓷 断面收缩率: .410% A一一试件原截面面积 A1一一拉断后颈缩处断面面积 6.卸载定律及冷作硬化 试件若拉到强化阶段,如d点卸载,则沿(dd')直线变化,短期内再 加载,仍然沿(dd')直线上升,说明比例极限提高,而延伸率降低,这种 现象称为冷作硬化现象。 「a.冷拔工艺,提高强度(如起重钢索,建筑用钢筋) 工程应用b.喷丸处理,提高表面强度(如机器零件表面形成冷硬层,提高抗疲劳强度) c滚压工艺,提高疲劳强度 缺陷:由于初加工,冷作硬化,使零件变硬变 1600 1600 脆,给机加工带来困难,为便于加工,需退火消除 120 冷硬层。 1100 1000 二、其他塑性材料拉伸时的力学性能 其他塑性材料:中碳钢、高碳钢、合金钢、铝 合金、青铜、黄铜。 051015202530354045505
l——原标距 l1——拉断后标距长度 塑性指标: δ>5%——塑性材料,钢、铜、铝 δ<5%——脆性材料,铸铁、玻璃、陶瓷 断面收缩率: ψ 1 100% − = A A A A——试件原截面面积 A1——拉断后颈缩处断面面积 6.卸载定律及冷作硬化 试件若拉到强化阶段,如 d 点卸载,则沿(dd′)直线变化,短期内再 加载,仍然沿(dd′)直线上升,说明比例极限提高,而延伸率降低,这种 现象称为冷作硬化现象。 滚压工艺,提高疲劳强度 喷丸处理,提高表面强度 如机器零件表面形成冷硬层,提高抗疲劳强度 冷拔工艺,提高强度 如起重钢索,建筑用钢筋 工程应用 . . ( ) . ( ) c b a 缺陷:由于初加工,冷作硬化,使零件变硬变 脆,给机加工带来困难,为便于加工,需退火消除 冷硬层。 二、其他塑性材料拉伸时的力学性能 其他塑性材料:中碳钢、高碳钢、合金钢、铝 合金、青铜、黄铜
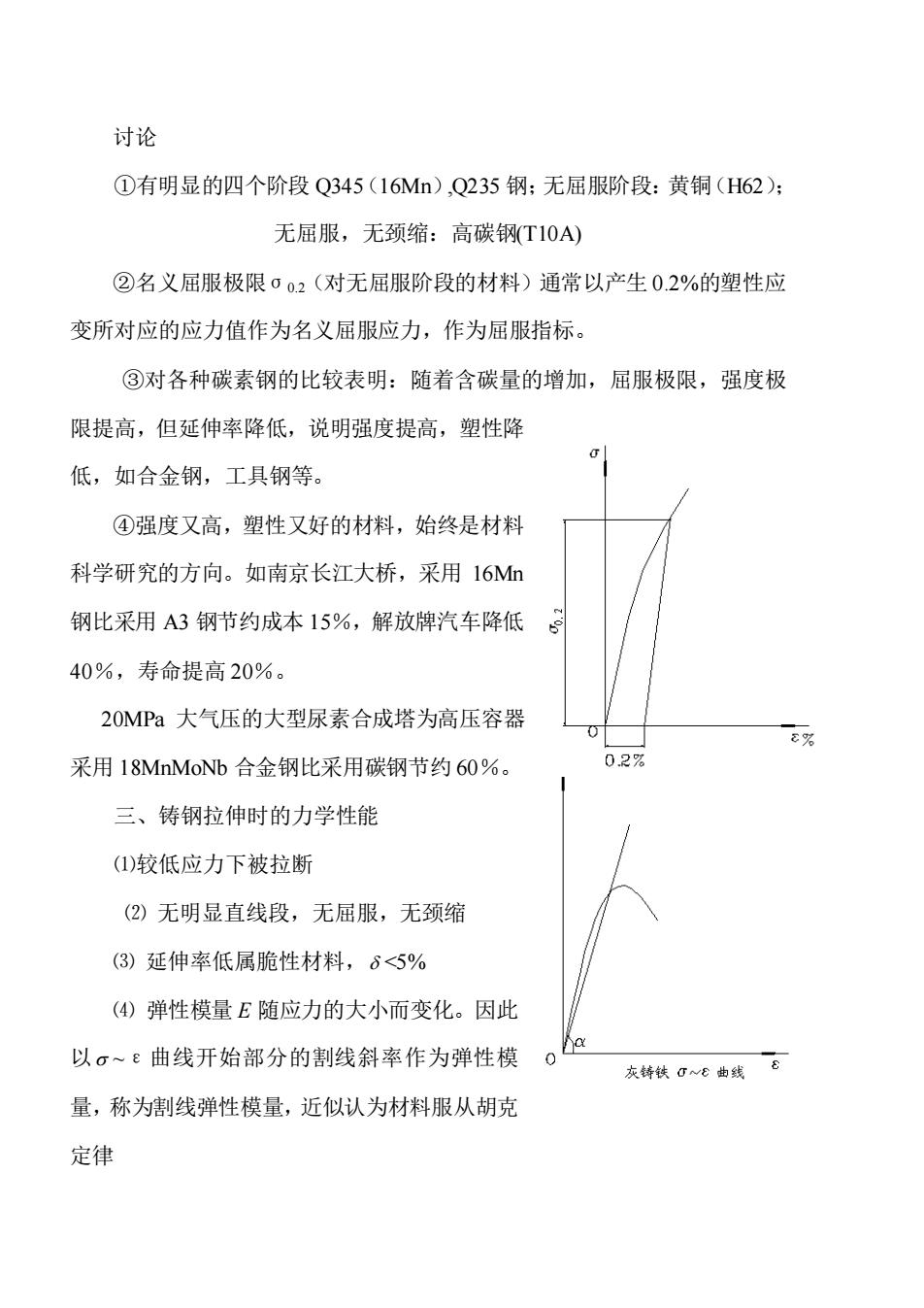
讨论 ①有明显的四个阶段Q345(16Mn),Q235钢:无屈服阶段:黄铜(H62): 无屈服,无颈缩:高碳钢(T10A) ②名义屈服极限σ02(对无屈服阶段的材料)通常以产生0.2%的塑性应 变所对应的应力值作为名义屈服应力,作为屈服指标。 ③对各种碳素钢的比较表明:随着含碳量的增加,屈服极限,强度极 限提高,但延伸率降低,说明强度提高,塑性降 低,如合金钢,工具钢等。 ④强度又高,塑性又好的材料,始终是材料 科学研究的方向。如南京长江大桥,采用16M 钢比采用A3钢节约成本15%,解放牌汽车降低 40%,寿命提高20%。 20MPa大气压的大型尿素合成塔为高压容器 % 采用18 MnMoNb合金钢比采用碳钢节约60%。 0.2% 三、铸钢拉伸时的力学性能 (1)较低应力下被拉断 (2)无明显直线段,无屈服,无颈缩 (3)延伸率低属脆性材料,6<5% (4)弹性模量E随应力的大小而变化。因此 以σ~ε曲线开始部分的割线斜率作为弹性模 0 灰铁G~e曲线8 量,称为割线弹性模量,近似认为材料服从胡克 定律
讨论 ①有明显的四个阶段 Q345(16Mn),Q235 钢;无屈服阶段:黄铜(H62); 无屈服,无颈缩:高碳钢(T10A) ②名义屈服极限σ0.2(对无屈服阶段的材料)通常以产生 0.2%的塑性应 变所对应的应力值作为名义屈服应力,作为屈服指标。 ③对各种碳素钢的比较表明:随着含碳量的增加,屈服极限,强度极 限提高,但延伸率降低,说明强度提高,塑性降 低,如合金钢,工具钢等。 ④强度又高,塑性又好的材料,始终是材料 科学研究的方向。如南京长江大桥,采用 16Mn 钢比采用 A3 钢节约成本 15%,解放牌汽车降低 40%,寿命提高 20%。 20MPa 大气压的大型尿素合成塔为高压容器 采用 18MnMoNb 合金钢比采用碳钢节约 60%。 三、铸钢拉伸时的力学性能 ⑴较低应力下被拉断 ⑵ 无明显直线段,无屈服,无颈缩 ⑶ 延伸率低属脆性材料, <5% ⑷ 弹性模量 E 随应力的大小而变化。因此 以 ~ε曲线开始部分的割线斜率作为弹性模 量,称为割线弹性模量,近似认为材料服从胡克 定律