
第一章绪论 §11材料力学的任务 §1.2变形固体的基本假设 §1.3外力及其分类 §1.4内力、截面法和应力的概念 §1.5变形与应变 §1.6杆件变形的基本形式 §1.1材料力学的任务 材料力学主要研究固体材料的宏观力学性能,构件的应力、变形 状态和破坏准则,以解决杆件或类似杆件的物件的强度、刚度和稳定 性等问题,为工程设计选用材料和构件尺寸提供依据。 材料的力学性能:如材料的比例极限、屈服极限、强度极限、延 伸率、断面收缩率、弹性模量、横向变形因数、硬度、冲击韧性、疲 劳极限等各种设计指标。它们都需要用实验测定。 构件的承载能力:强度、刚度、稳定性。 构件:机械或设备,建筑物或结构物的每一组成部分。 强度:构件抵抗破坏(断裂或塑性变形)的能力。 所有的机械或结构物在运行或使用中,其构件都将受到一定的力 作用,通常称为构件承受一定的载荷,但是对于构件所承受的载荷都 有一定的限制,不允许过大,如果过大,构件就会发生断裂或产生塑 性变形而使构件不能正常工作,称为失效或破坏,严重者将发生工程 事故。如飞机坠毁、轮船沉没、锅炉爆炸、曲轴断裂、桥梁折断、房
第一章 绪论 §1.1 材料力学的任务 §1.2 变形固体的基本假设 §1.3 外力及其分类 §1.4 内力、截面法和应力的概念 §1.5 变形与应变 §1.6 杆件变形的基本形式 §1.1 材料力学的任务 材料力学主要研究固体材料的宏观力学性能,构件的应力、变形 状态和破坏准则,以解决杆件或类似杆件的物件的强度、刚度和稳定 性等问题,为工程设计选用材料和构件尺寸提供依据。 材料的力学性能:如材料的比例极限、屈服极限、强度极限、延 伸率、断面收缩率、弹性模量、横向变形因数、硬度、冲击韧性、疲 劳极限等各种设计指标。它们都需要用实验测定。 构件的承载能力:强度、刚度、稳定性。 构件:机械或设备,建筑物或结构物的每一组成部分。 强度:构件抵抗破坏(断裂或塑性变形)的能力。 所有的机械或结构物在运行或使用中,其构件都将受到一定的力 作用,通常称为构件承受一定的载荷,但是对于构件所承受的载荷都 有一定的限制,不允许过大,如果过大,构件就会发生断裂或产生塑 性变形而使构件不能正常工作,称为失效或破坏,严重者将发生工程 事故。如飞机坠毁、轮船沉没、锅炉爆炸、曲轴断裂、桥梁折断、房

屋坍塌、水闸被冲垮,轻者毁坏机械设备、停工停产、重者造成工程 事故,人身伤亡,甚至带来严重灾难。工程中的事故屡见不鲜,有些 触目惊心,惨不忍睹.因此必须研究受载构件抵抗破坏的能力一 强度,进行强度计算,以保证构件有足够的强度。 刚度一一构件抵抗变形的能力。 当构件受载时,其形状和尺寸都要发生变化,称为变形。工程中 要求构件的变形不允许过大,如果过大构件就不能正常工作。如机床 的齿轮轴,变形过大就会造成齿轮啮合不良,轴与轴承产生不均匀磨 损,降低加工精度,产生噪音;再如吊车大梁变形过大,会使跑车出 现爬坡,引起振动;铁路桥梁变形过大,会引起火车脱轨,翻车. 因此必须研究构件抵抗变形的能力一刚度,进行刚度计算,以保证 构件有足够的刚度。 稳定性一一构件保持原来平衡形态的能力。 如细长的活塞杆或者连杆,当诸如此类的细长杆子受压时,工程 中要求它们始终保持直线的平衡形态。可是若受力过大,压力达到某 一数值时,压杆将由直线平衡形态变成曲线平衡形态,这种现象称之 为压杆的失稳。又如受均匀外压力的薄壁圆筒,当外压力达到某一数 值时,它由原来的圆筒形的平衡变成椭圆形的平衡,此为薄圆筒的失 稳。失稳往往是突然发生而造成严重的工程事故,如19世纪未,瑞 士的孟希太因大桥,20世纪初加拿大的魁北克大桥都由于桥架受压 弦杆失稳而突然使大桥坍塌。.因此必须研究构件保持原来形态能 力一一稳定性,进行稳定性计算,以保持构件有足够的稳定性
屋坍塌、水闸被冲垮,轻者毁坏机械设备、停工停产、重者造成工程 事故,人身伤亡,甚至带来严重灾难。工程中的事故屡见不鲜,有些 触目惊心,惨不忍睹.因此必须研究受载构件抵抗破坏的能力—— 强度,进行强度计算,以保证构件有足够的强度。 刚度——构件抵抗变形的能力。 当构件受载时,其形状和尺寸都要发生变化,称为变形。工程中 要求构件的变形不允许过大,如果过大构件就不能正常工作。如机床 的齿轮轴,变形过大就会造成齿轮啮合不良,轴与轴承产生不均匀磨 损,降低加工精度,产生噪音;再如吊车大梁变形过大,会使跑车出 现爬坡,引起振动;铁路桥梁变形过大,会引起火车脱轨,翻车. 因此必须研究构件抵抗变形的能力——刚度,进行刚度计算,以保证 构件有足够的刚度。 稳定性——构件保持原来平衡形态的能力。 如细长的活塞杆或者连杆,当诸如此类的细长杆子受压时,工程 中要求它们始终保持直线的平衡形态。可是若受力过大,压力达到某 一数值时,压杆将由直线平衡形态变成曲线平衡形态,这种现象称之 为压杆的失稳。又如受均匀外压力的薄壁圆筒,当外压力达到某一数 值时,它由原来的圆筒形的平衡变成椭圆形的平衡,此为薄圆筒的失 稳。失稳往往是突然发生而造成严重的工程事故,如 19 世纪末,瑞 士的孟希太因大桥,20 世纪初加拿大的魁北克大桥都由于桥架受压 弦杆失稳而突然使大桥坍塌。.因此必须研究构件保持原来形态能 力——稳定性,进行稳定性计算,以保持构件有足够的稳定性

§1.2变形固体的基本假设 刚体一一假定受力时不发生变形的物体。 适用于理论力学研究物体的外部效应—平衡和运动。 变形固体一—一在外力作用下发生变形的物体。 变形固体的实际组成及其性质是很复杂的,为了分析和简化计算 将其抽象为理想模型,作如下基本假设: 1)连续性假设:认为组成固体的物质不留空隙地充满了固体的 体积。(某些力学量可作为点的坐标的函数) 2)均匀性假设:认为固体内到处有相同的力学性能。 3)各向同性假设:认为无论沿任何方向固体的力学性能都是相 同的。 各向同性材料:如钢、铜、玻璃等。 各向异性材料:如材料、胶合板,某些人工合成材料、复合材料 等
§1.2 变形固体的基本假设 刚体——假定受力时不发生变形的物体。 适用于理论力学研究物体的外部效应——平衡和运动。 变形固体——在外力作用下发生变形的物体。 变形固体的实际组成及其性质是很复杂的,为了分析和简化计算 将其抽象为理想模型,作如下基本假设: 1) 连续性假设:认为组成固体的物质不留空隙地充满了固体的 体积。(某些力学量可作为点的坐标的函数) 2) 均匀性假设:认为固体内到处有相同的力学性能。 3) 各向同性假设:认为无论沿任何方向固体的力学性能都是相 同的。 各向同性材料:如钢、铜、玻璃等。 各向异性材料:如材料、胶合板,某些人工合成材料、复合材料 等

§1.3外力及其分类 体力自重力(N/m 惯性力(N/m) 作用方式 分布力面分布力(N/m) 外使我动 面 线分布力(N/m) 集中力(N、kN) [静载荷 变化与 动载荷冲击载荷 交变载荷 载荷一一作用于构件上的主动力 体积力一一—连续分布在物体内各点的力 面积力—一作用于物体表面上的力 面分布力一一连续分布于物体表面某一面积上的力 线分布力一一沿着物体某一轴线上分布的力 集中力一一若作用面积远小于物体整体尺寸或线性分布长度远小于 轴线长度 静载荷一一若载荷从零开始缓慢增加到某值后保持不变或变化很小 动载荷—一随时间而变化的载荷 冲击载荷一一由于物体运动状态瞬时发生突然变化而引起的载荷 交变载荷一一随时间而发生周期性变化的载荷 §1.4内力、截面法和应力的概念 1.内力(附加内力) 物体因受外力而变形,其内部各部分之间相对位置将发生改变而 引起的相互作用就是内力
§1.3 外力及其分类 交变载荷 冲击载荷 动载荷 静载荷 变化与否 集中力( 、 ) 线分布力( ) 面分布力( ) 分布力 面力 惯性力( ) 自重力( ) 体力 作用方式 支反力 载荷 外力 N kN N / m N / m N / m N / m 2 3 3 载荷——作用于构件上的主动力 体积力——连续分布在物体内各点的力 面积力——作用于物体表面上的力 面分布力——连续分布于物体表面某一面积上的力 线分布力——沿着物体某一轴线上分布的力 集中力——若作用面积远小于物体整体尺寸或线性分布长度远小于 轴线长度 静载荷——若载荷从零开始缓慢增加到某值后保持不变或变化很小 动载荷——随时间而变化的载荷 冲击载荷——由于物体运动状态瞬时发生突然变化而引起的载荷 交变载荷——随时间而发生周期性变化的载荷 §1.4 内力、截面法和应力的概念 1. 内力(附加内力) 物体因受外力而变形,其内部各部分之间相对位置将发生改变而 引起的相互作用就是内力

当物体不受外力作用时,内部各质点之间存在着相互作用力,此 为内力。但材料力学中所指的内力是与外力和变形有关的内力。即随 若外力的作用而产生,随着外力的增加而增大,当达到一定数值时会 引起构件破坏的内力,此力称为附加内力。为简便起见,今后统称为 内力。 2.截面法 为进行强度、刚度计算必须由已知的外力确定未知的内力,而内 力为作用力和反作用力,对整体而言不出现,为此必须采用截面法, 将内力暴露。 截面法三步骤 (1)切:欲求某一截面上的内力,即用一假想平面将物体分为两部 分 (2)代:两部分之间的相互作用用力代替 (3)平:建立其中任一部分的平衡条件,求未知内力 注:内力为连续分布力,用平衡方程,求其分布内力的合力 上述步骤可以叙述为:一截为二,去一留一,平衡求力
当物体不受外力作用时,内部各质点之间存在着相互作用力,此 为内力。但材料力学中所指的内力是与外力和变形有关的内力。即随 着外力的作用而产生,随着外力的增加而增大,当达到一定数值时会 引起构件破坏的内力,此力称为附加内力。为简便起见,今后统称为 内力。 2. 截面法 为进行强度、刚度计算必须由已知的外力确定未知的内力,而内 力为作用力和反作用力,对整体而言不出现,为此必须采用截面法, 将内力暴露。 截面法三步骤: (1)切 :欲求某一截面上的内力,即用一假想平面将物体分为两部 分 (2)代 :两部分之间的相互作用用力代替 (3)平:建立其中任一部分的平衡条件,求未知内力 注:内力为连续分布力,用平衡方程,求其分布内力的合力 上述步骤可以叙述为:一截为二,去一留一,平衡求力
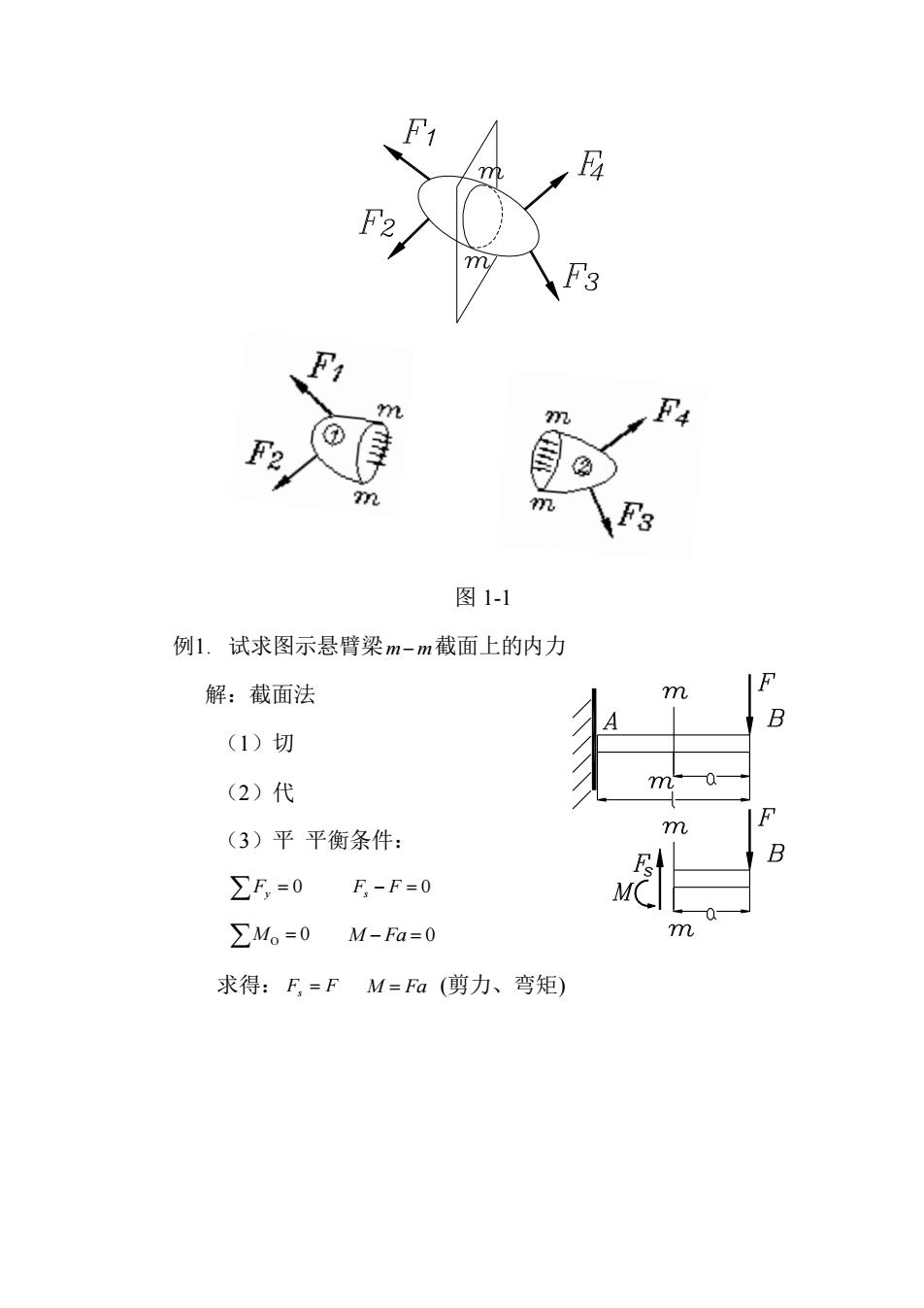
F3 m F2 m Fs 图1-1 例1.试求图示悬臂梁m-m截面上的内力 解:截面法 m (1)切 (2)代 m 0 (3)平平衡条件: ∑F,=0F-F=0 ∑Mo=0M-Fa=0 m 求得:F=FM=Fa(剪力、弯矩)
图 1-1 例1. 试求图示悬臂梁 m−m 截面上的内力 解:截面法 (1)切 (2)代 (3)平 平衡条件: Fy = 0 Fs − F = 0 MO = 0 M − Fa = 0 求得: Fs = F M = Fa (剪力、弯矩)

3.应力 △A m m 因内力为分布力系,为研究内力在截面上的分布规律,引入内力 集度的概念 P.t P. △,上的平均集度,称为平均应力上的平均集度,称为平均 应力 F P=M p一C点的内力集度,称为C点处总应力,p为矢量。 1Pa =IN/m2 IMPa =Ix10 Pa 应力单位: IN/mm2=IMPa M. §1.5变形与应变 变形一一物体受力后形状和尺寸的改变 1.线应变(简称应变) 假设:固体受到约束无刚体位移,只有变 L'laxtas 形位移,若有刚体位移,应从总位移中扣除
3. 应力 因内力为分布力系,为研究内力在截面上的分布规律,引入内力 集度的概念 A F pm = m p ——A上的平均集度,称为平均应力 上的平均集度,称为平均 应力 A F p p A m A = = →0 →0 lim lim p —— C点的内力集度,称为C点处总应力,p为矢量。 − − --切应力 正应力 p 应力单位: 1N/mm 1MPa 2 = §1.5 变形与应变 变形——物体受力后形状和尺寸的改变 1. 线应变(简称应变) 假设:固体受到约束无刚体位移,只有变 形位移,若有刚体位移,应从总位移中扣除。 2 1Pa =1N/m 1MPa 1x10 Pa 6 =
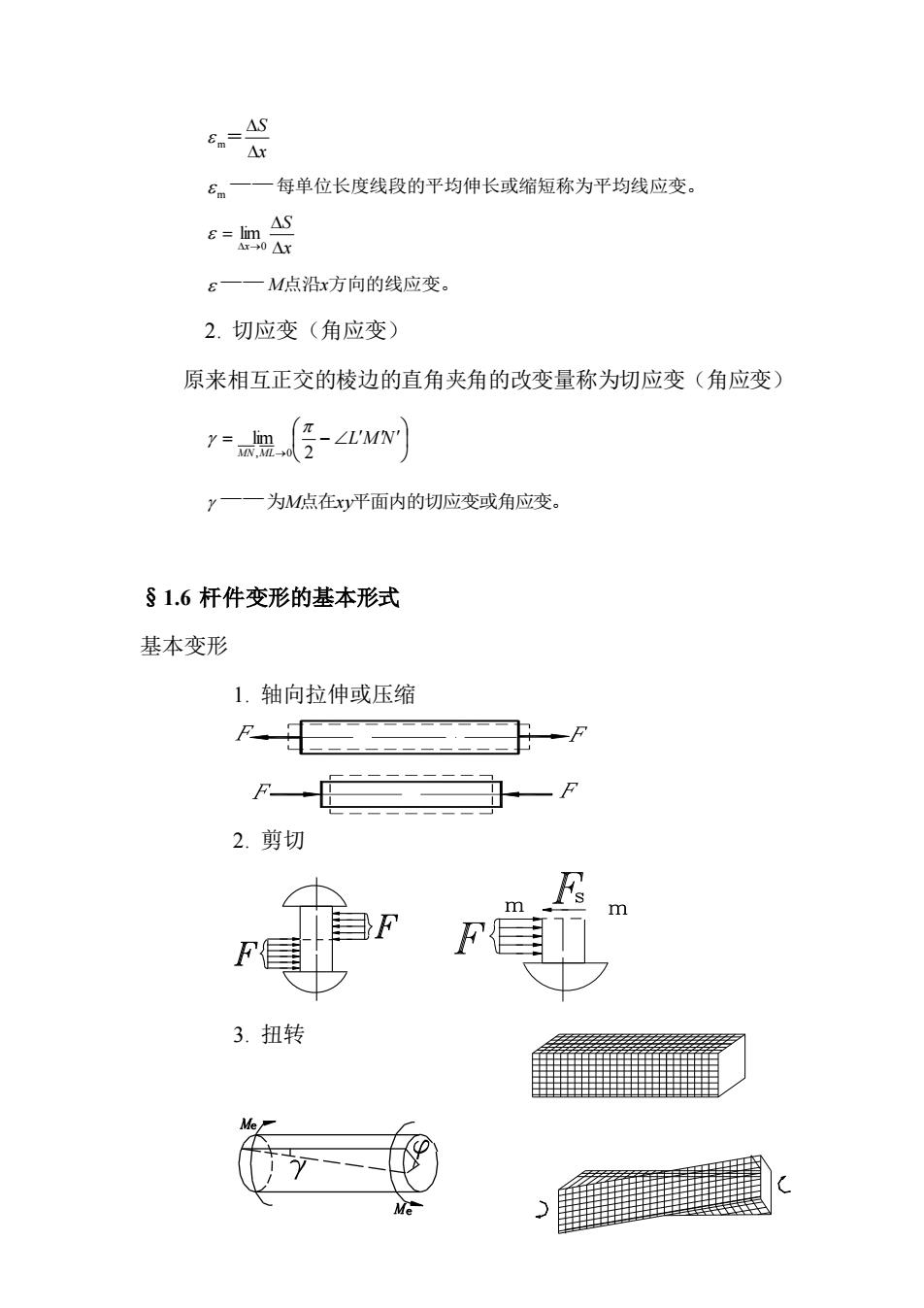
5。一—每单位长度线段的平均伸长或缩短称为平均线应变。 68 E一一M点沿x方向的线应变 2.切应变(角应变) 原来相互正交的棱边的直角夹角的改变量称为切应变(角应变) 7是导-wN网 y一一为M点在y平面内的切应变或角应变。 §1.6杆件变形的基本形式 基本变形 1.轴向拉伸或压缩 F 2.剪切 3.扭转
x S m = m ——每单位长度线段的平均伸长或缩短称为平均线应变。 x S x = →0 lim ——M点沿x方向的线应变。 2. 切应变(角应变) 原来相互正交的棱边的直角夹角的改变量称为切应变(角应变) = − → L M N MN ML 2 lim , 0 ——为M点在xy平面内的切应变或角应变。 §1.6 杆件变形的基本形式 基本变形 1. 轴向拉伸或压缩 2. 剪切 3. 扭转

4.弯曲 -Z公 组合变形:当杆件同时发生两种或两种以上基本变形时称为组合变 形
4. 弯曲 组合变形:当杆件同时发生两种或两种以上基本变形时称为组合变 形。 FP M M FP