
第六章弯曲变形 §6.1工程中的弯曲变形问题 §6.2挠曲线的微分方程 §6.3用积分法求弯曲变形 §6.4用叠加法求弯曲变形 §6.5简单超静定梁 §6.6提高弯曲刚度的一些措施 §6.1工程中的弯曲变形问题 1.实例 ①车床主轴:变形过大,会使齿轮啮合不良,轴与轴承产生非均匀磨 损,产生噪声,降低寿命,影响加工精度。 ②吊车梁:变形过大会出现小车爬坡现象,引起振动。 2.研究变形目的 ①建立刚度条件,解决刚度问题 ②建立变形协调条件,解决超静定问题 ③为振动计算奠定基础。 §6.2挠曲线的微分方程 1.概念 以简支梁为例,以变形前的轴线为x轴,垂直向上为y轴,Oy平面
第六章 弯曲变形 §6.1 工程中的弯曲变形问题 §6.2 挠曲线的微分方程 §6.3 用积分法求弯曲变形 §6.4 用叠加法求弯曲变形 §6.5 简单超静定梁 §6.6 提高弯曲刚度的一些措施 §6.1 工程中的弯曲变形问题 1. 实例 ①车床主轴:变形过大,会使齿轮啮合不良,轴与轴承产生非均匀磨 损,产生噪声,降低寿命,影响加工精度。 ②吊车梁:变形过大会出现小车爬坡现象,引起振动。 2. 研究变形目的 ①建立刚度条件,解决刚度问题 ②建立变形协调条件,解决超静定问题 ③为振动计算奠定基础。 §6.2 挠曲线的微分方程 1. 概念 以简支梁为例,以变形前的轴线为 x 轴,垂直向上为 y 轴,xoy 平面
为梁的纵向对称面。 ①挠曲线: Y 在对称弯曲情况下,变形后梁的轴 线为xoy平面内的一条曲线,此曲线称 f(x 为挠曲线。 ②挠度: 梁的任一截面形心的竖直位移称为挠度。 ③挠曲线的方程式: w-fx) ④转角:弯曲变形中,梁的横截面对其原来位置转过的角度0,称 为截面转角。根据平面假设,梁的横截面变形前,垂直于轴线,变形后 垂直于挠曲线。故 转角©1挠曲线的法线与轴的夹角 2.挠曲线的切线与x轴的夹角 m0架 0- y ⑤挠度w和转角9是度量弯曲 变形的两个基本量。 ds ⑥挠度与转角符号规定:在图 示坐标中,挠度向上为正, 0 】0 0+d dx 反时针的转角为正。 2.挠曲线的曲率表示式:
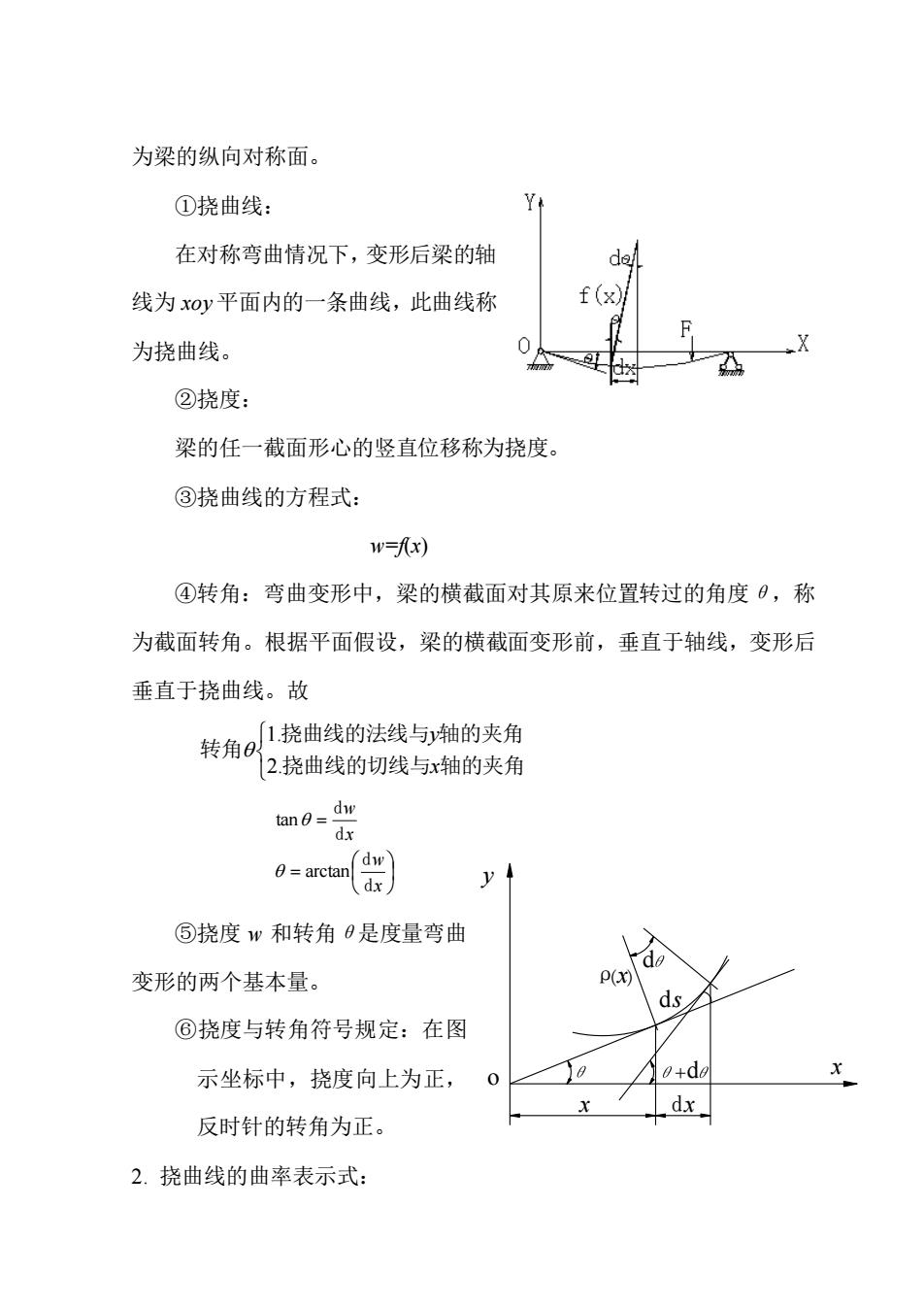
为梁的纵向对称面。 ①挠曲线: 在对称弯曲情况下,变形后梁的轴 线为 xoy 平面内的一条曲线,此曲线称 为挠曲线。 ②挠度: 梁的任一截面形心的竖直位移称为挠度。 ③挠曲线的方程式: w=f(x) ④转角:弯曲变形中,梁的横截面对其原来位置转过的角度θ,称 为截面转角。根据平面假设,梁的横截面变形前,垂直于轴线,变形后 垂直于挠曲线。故 挠曲线的切线与 轴的夹角 挠曲线的法线与 轴的夹角 转角 x y 2. 1. = = x w x w d d d d arctan tan ⑤挠度 w 和转角θ是度量弯曲 变形的两个基本量。 ⑥挠度与转角符号规定:在图 示坐标中,挠度向上为正, 反时针的转角为正。 2. 挠曲线的曲率表示式: o y x s + d ρ d ( )x d d x x
①纯弯面:。出 ②横力言角:南四 细长梁么≥5,忽略F影响。 3.挠曲线的曲率表达式 ①纯弯曲: 日台 (a) M M ②横力弯曲: M>0 M<0 对细长梁而言,忽略剪力F的影 0 <0 0 X 响 和 (b) ③高等数学中对曲率的定义 及表达式 lds pldo 1de ds dx p ds 于是式(a)转化为 doM dsEI (c) 在我们选定的坐标系内,若弯矩M为正,则挠曲线向下凸,(如图所示), 随着弧长S的增加,O也是增加的,即正增量ds对应的d8也是正的,于 是考虑符号后,式(c)可写成 (d)
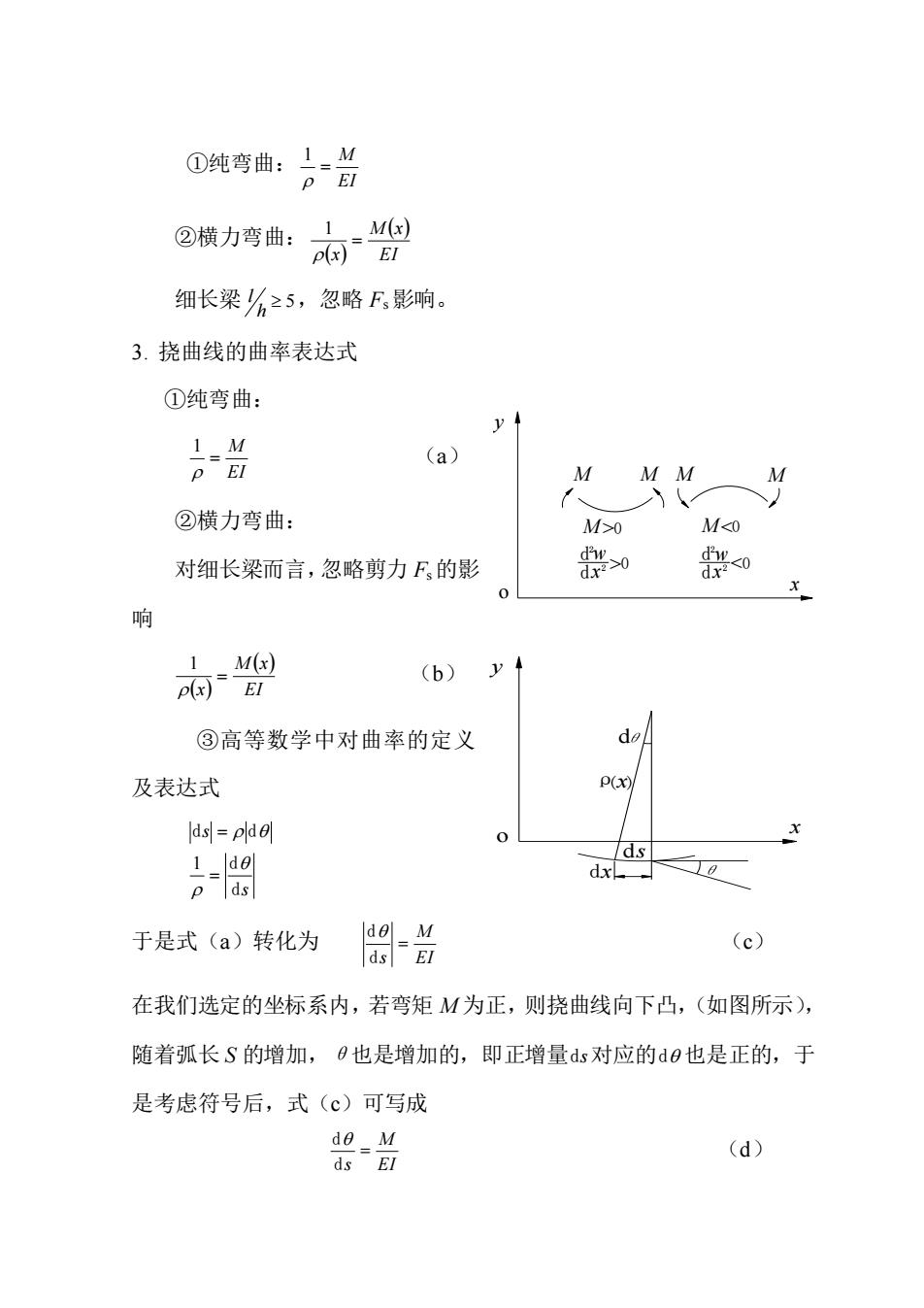
①纯弯曲: EI M = 1 ②横力弯曲: ( ) ( ) EI M x x = 1 细长梁 5 h l ,忽略 Fs 影响。 3. 挠曲线的曲率表达式 ①纯弯曲: EI M = 1 (a) ②横力弯曲: 对细长梁而言,忽略剪力 Fs 的影 响 ( ) ( ) EI M x x = 1 (b) ③高等数学中对曲率的定义 及表达式 s s d d d d = = 1 于是式(a)转化为 EI M s = d d (c) 在我们选定的坐标系内,若弯矩 M 为正,则挠曲线向下凸,(如图所示), 随着弧长 S 的增加,θ也是增加的,即正增量 ds 对应的 d 也是正的,于 是考虑符号后,式(c)可写成 EI M s = d d (d) y o x >0 0 2 0 dx 2 d < M M M M M M w w x y o d ρ( )x ds dx

m0出 d-w = dx2 dx 1+ ds=ar+ao时-d 注意到 d ds 代入式(d)及: d2w M (e) (dw E 此为挠曲线的微分方程,适用于弯曲变形的任意情况,它是非线性的。 在小变形的情况下,梁的挠度w一般都远小于跨度,挠曲线w=f是一 非常平坦的曲线,转角日也是一个非常小的角度,于是 0em0-张=8 (f) 式(e)中(a,于是式(e)可写成 d'w M dx?EI (g) 此式为挠曲线的近似微分方程
x w d d tan = s x x w s x x s x d d d d d d d d d d d d = = arctan s x x w x w d d d d d d 2 2 2 1 + = 注意到 ( ) ( ) 3 2 d d d d d d d d d d d d + = = + = + 2 2 2 2 2 2 1 1 x w x w s x x w s x w 代入式(d)及: EI M x w x w = + 3 2 2 2 2 1 d d d d (e) 此为挠曲线的微分方程,适用于弯曲变形的任意情况,它是非线性的。 在小变形的情况下,梁的挠度 w 一般都远小于跨度,挠曲线 w=f(x)是一 非常平坦的曲线,转角θ也是一个非常小的角度,于是 f (x) x w tan = = ' d d (f) 式(e)中 1 2 x w d d ,于是式(e)可写成 EI M x w = 2 2 d d (g) 此式为挠曲线的近似微分方程

§6.3用积分法求弯曲变形 1.挠曲线的近似微分方程 d2w M X=a,W=0 dx2EI 对等直梁而言,E1为常量,于是上式可写成0 a胺=M x=b,W=0 a 积分可得转角方程,再积分可得挠曲线方程0 sc y 以 X=C,W=0 Ehw=∫[MxHr+Cx+D a 式中C,D为积分常数,可由边界条件及连0 续条件确定。 2.边界条件: 在挠曲线的某些点上,挠度或转角有时是已知的这类条件称为边界 条件。 3.连续条件: 挠曲线是一条光滑连续的曲线,在挠曲线的任一点上有唯一确定的 挠度和转角这就是连续条件。 4.刚度条件: hwls [w]l lol.s[] Examplel.EJ=const
§6.3 用积分法求弯曲变形 1. 挠曲线的近似微分方程 EI M x w = 2 2 d d 对等直梁而言,EI 为常量,于是上式可写成 M x w EI = 2 2 d d 积分可得转角方程,再积分可得挠曲线方程 = M x + C x w EI d d d EIw = Mdx dx + Cx + D 式中 C、D 为积分常数,可由边界条件及连 续条件确定。 2. 边界条件: 在挠曲线的某些点上,挠度或转角有时是已知的这类条件称为边界 条件。 3. 连续条件: 挠曲线是一条光滑连续的曲线,在挠曲线的任一点上有唯一确定的 挠度和转角这就是连续条件。 4. 刚度条件: t w w w x m x Example1. EI=const x x x a o y a a o o y y =0 =c, =0 =b, =0 x=a, =0 x x

Find. wax、0ma Solution. y ①列弯矩方程: M)=-'。 9r3 (0≤x<D ②列微分方程及积分 Ehw-jq EN=EI0-+C E=-249m+G+D ③求积分常数 边界条件:当x=1时,W=0=0,w=0 C-gaP D-gal ④转角方程及挠度方程: =4m+名- ⑤求041w4 将=0代入以上二式 6EI ”器
Find. wmax、θmax Solution. ①列弯矩方程: ( ) 2 2 1 M x = − qx (0≤x<l) ②列微分方程及积分 EIw qx Cx D EIw EI qx C EIw qx = − + + = = − + = − 4 3 2 24 1 6 1 ' 2 1 '' ③求积分常数 边界条件:当 x=l 时, w'=θ=0,w=0 3 6 1 C = ql 4 8 1 D = − ql ④转角方程及挠度方程: 4 3 4 3 3 8 1 6 1 24 1 6 1 6 1 ' EIw qx ql x ql EIw EI qx ql = − + − = = − + ⑤求θA, wA 将 x=0 代入以上二式 EI ql A 6 3 = EI ql wA 8 4 = − q L A y

Example2.内燃机的凸轮轴或齿轮轴计算简图,试求转角方程及挠度方 程,wmax、max o y Solution 0求反加:R中= Fa ②列弯矩方程: (AC)M-EE (0≤x1≤a) (CB)M,) (a≤x≤ ③列微分方程及积分 (AC) E-色 EhiCI B-碧+CX+D (CB) -P6-0) -5-+c E-6-+c+n ④求积分常数 边界条件:当x=0时,w1=0 当x2=时,w2=0 连续条件:当x=x2=a时,w1=w2,W=W2
Example2. 内燃机的凸轮轴或齿轮轴计算简图,试求转角方程及挠度方 程,wmax、θmax。 Solution ①求反力: l Fa F l Fb FRA = , RB = ②列弯矩方程: (AC) 1 1 x l Fb M = (0≤x1≤a) (CB) x F(x a) l Fb M 2 = 2 − 2 − (a≤x2≤l) ③列微分方程及积分 (AC) = + + = + = 1 1 1 3 1 1 1 2 1 '' 1 1 '' 1 6 2 x C X D l Fb EIw x C l Fb EIw x l Fb EIw (CB) ( ) ( ) ( ) = − − + + = − − + = − − 2 2 2 3 2 3 2 2 2 2 2 2 2 ' 2 2 2 '' 2 6 6 2 2 x a C X D F x l Fb EIw x a C F x l Fb EIw x F x a l Fb EIw ④求积分常数 边界条件:当 x1=0 时,w1=0 当 x2=l 时,w2=0 连续条件:当 x1=x2=a 时,w1 1= w1 2 ,w1= w2 C b B L x2 a RA A x y RB F

G=60e-川 D1=D2=0 ⑤转角方程及挠度方程 (AC) -x+6-) (a) -+6-rh灯 (6) (CB) Em=对-5k,-a}+6-r) c 1 ,音-+e- (d) ⑥最大挠度wm,最大转角日m 当=0时,0,=-Fal+ 6E1 当=时,8,=Fab+a 6E7 若a>b,则9.9,l,0mx>0B 若ab,则0c为正值。可见从截面A到截面C转角由负变正,改变 了符号,挠曲线既为光滑连续曲线,00的截面必然在(AC)段。令式 (a)等于零:
( ) 2 2 1 2 6 b l l Fb C = C = − D1=D2=0 ⑤转角方程及挠度方程 (AC) ( ) ( ) = + − = + − 1 3 2 2 1 1 2 2 2 1 ' 1 6 3 6 x b l x l Fb EIw x b l l Fb EIw ( ) (b) a (CB) ( ) ( ) ( ) ( ) = − − + − = − − + − 3 2 2 2 3 2 2 2 2 2 2 2 2 ' 2 6 6 6 2 2 6 b l l Fb x a F x l Fb EIw b l l Fb x a F x l Fb EIw ( ) (d ) c ⑥最大挠度 wmax,最大转角θmax 当 x1=0 时, ( ) EIl Fab l b A 6 + = − 当 x2=l 时, ( ) EIl Fab l a B 6 + = 若 a>b,则 B A ,θmax>θB 若 a<b,则 B A max = A 最大挠度 wmax 当 ' = = = 0. x w w d d 时,w 为极值,所以应首先确定 为零的截面位置。若 在式(a)中,令 x1=a,可求的 (a b) EIl Fab c = − 3 若 a>b,则θC为正值。可见从截面 A 到截面 C 转角由负变正,改变 了符号,挠曲线既为光滑连续曲线,θ=0 的截面必然在(AC)段。令式 (a)等于零:

6x+b-P)=0 61 即为挠度为最大值的截面横坐标。以和代入式(b)的最大挠度 =小、品0- 当F作用于中点时,即a=b= 号一子最大挠度发生在中点。 FP wm="/48E 极端情况,当F无限接近右支座时,b2<<P,b2可以省略,于是 =方-05m Fbl2 w.-9J3EI 可见即是在这种极端情况下,最大挠度仍然发生在跨度中点附近,也就 是最大挠度总在靠近跨度中点。所以可 以用跨度中点的挠度近似代替最大挠A工B 度,因此,在式(0)中令x=号求出骑 L2↓2 度中点挠度为: ”g=-盈6r-) 即是在极端情况下,b→0时 212 Fb Fbl LL2⊥L2J
( ) 3 3 0 6 2 2 0 2 2 2 0 l b x x b l l Fb − = + − = x0即为挠度为最大值的截面横坐标。以 x0代入式(b)的最大挠度 ( ) 3 2 2 max 1 9 3 1 0 l b EIl Fb w = w x =x = − − 当 F 作用于中点时,即 2 , 2 0 l x l a = b = = ,最大挠度发生在中点。 EI Fl w w x x 48 3 2 max 1 1 0 = = − = = 极端情况,当 F 无限接近右支座时,b 2<< l 2,b 2可以省略,于是 EI Fbl w l l x 9 3 0.577 3 2 max 0 = − = = 可见即是在这种极端情况下,最大挠度仍然发生在跨度中点附近,也就 是最大挠度总在靠近跨度中点。所以可 以用跨度中点的挠度近似代替最大挠 度,因此,在式(b)中令 2 1 l x = 求出跨 度中点挠度为: ( ) 2 2 3 4 2 48 l b EI Fb w l = − − 即是在极端情况下,b→0 时 EI Fbl l EI Fb w l 16 3 48 2 2 2 = −

⑦误差分析: 用wx代替Wax所引起的误差 "=-0生=265% Wmx ⑧结论 可见在简支梁中,只要挠曲线无拐点,总可用跨度中点的挠度代替 最大挠度不会引起很大误差。 §6.4用叠加法求弯曲变形 1.积分法 ①优点:可以求得挠曲线的转角方程和挠曲线方程,因此可求任意截 面的转角和挠度是最基本的方法。 ②缺点:积分法比较麻烦。 2.叠加法 ①在小变形,线弹性前提下(材料服从胡克定律),挠度与转角均与载 荷成线性关系。因此,当梁上有多个载荷作用时,可以分别求出每 一载荷单独引起的变形,把所得变形叠加即为这些载荷共同作用时 的变形,这就是弯曲变形的叠加法。 ②为了便于工程计算,把简单基本载荷作用下梁的挠曲线方程,最大挠 度,最大转角计算公式编入手册,以便查用。P1881 Example 1 Given:EI=const Find:0A.B.Wc
⑦误差分析: 用 2 l w 代替 wmax所引起的误差 2.65% max max 2 = − w w L ⑧结论 可见在简支梁中,只要挠曲线无拐点,总可用跨度中点的挠度代替 最大挠度不会引起很大误差。 §6.4 用叠加法求弯曲变形 1. 积分法 ①优点:可以求得挠曲线的转角方程和挠曲线方程,因此可求任意截 面的转角和挠度是最基本的方法。 ②缺点:积分法比较麻烦。 2. 叠加法 ①在小变形,线弹性前提下(材料服从胡克定律),挠度与转角均与载 荷成线性关系。因此,当梁上有多个载荷作用时,可以分别求出每 一载荷单独引起的变形,把所得变形叠加即为这些载荷共同作用时 的变形,这就是弯曲变形的叠加法。 ②为了便于工程计算,把简单基本载荷作用下梁的挠曲线方程,最大挠 度,最大转角计算公式编入手册,以便查用。P188-1 Example 1 Given: EI = const Find:θA, θB, wC