
强度理论 典型习题解析 1已知铸铁的拉伸许用应力[o,J=30MPa,压缩许用应力[GJ=90MPa,4=0.30,试对铸 铁零件进行强度校核,危险点的主应力为: (1)G1=30MP,O2=20MPa,a3=15MPa: (2)1=-20MPa,g2=-30MPa,G3=-40MPa: (3)o1=10MPa,c2=-20MP,o3=-30MPa· 解题分析:选用强度理论时,不但要考虑材料是脆性或是塑性,还要考虑危险点处的应力状 态。 解:(1)G1=30MPa,2=20MP,5=15MPa,危险点处于三向拉应力状态,不论材 料本身是塑性材料或是脆性材料,均采用第一强度理论,即: H=1=30MPa=[J,安全 (2)c=-20MPa,2=-30MPa,C=-40MPa,危险点处于三向压应力状态,即使是 脆性材料,也应采用第三或第四强度理论,即: c3=o1-G3=-20MPa-(-40MPa=20MPa<G,J,安全 o4=5I-20MPa+30MP)'+(-30MP+40MPa)2+(-40MP+20MPa)'] =17.3MPa<[aJ,安全。 (3)1=10MP,2=-20MP,3=-30MP,脆性材料的危险点处于以压应力为主 的应力状态,且许用拉应力与许用压应力不等,宜采用莫尔强度理论,即: 2图示实心圆轴受轴向外力F和外力偶M作用。己知圆轴直径本10mm,M仁Fd10。(1) 材料为钢时,许用应力[]=160MPa:材料为铸铁时,许用应力[a]=30MP,试分别计算 圆轴的许可载荷F:(2)材料为铸铁,且F=2kN、E=100GPa、4=025,计算圆轴表面 上与轴线成30°方位上的正应变
强度理论 典型习题解析 1 已知铸铁的拉伸许用应力[ ] 30MPa σ t = ,压缩许用应力[ ] 90 MPa σ c = , µ = 0.30 ,试对铸 铁零件进行强度校核,危险点的主应力为: (1) 30MPa σ 1 = , 20MPa σ 2 = , 15MPa σ 3 = ; (2) 20MPa σ 1 = − , 30MPa σ 2 = − , 40MPa σ 3 = − ; (3) 10MPa σ 1 = , 20MPa σ 2 = − , 30MPa σ 3 = − 。 解题分析:选用强度理论时,不但要考虑材料是脆性或是塑性,还要考虑危险点处的应力状 态。 解:(1) 30MPa σ 1 = , 20MPa σ 2 = , 15MPa σ 3 = ,危险点处于三向拉应力状态,不论材 料本身是塑性材料或是脆性材料,均采用第一强度理论,即: 30MPa [ ] σ r1 = σ 1 = = σ t ,安全 (2) 20MPa σ 1 = − , 30MPa σ 2 = − , 40MPa σ 3 = − ,危险点处于三向压应力状态,即使是 脆性材料,也应采用第三或第四强度理论,即: 20MPa ( 40)MPa 20MPa [ ] σ r3 = σ 1 −σ 3 = − − − = < σ t ,安全 [( 20 MPa 30 MPa) ( 30MPa 40 MPa) ( 40 MPa 20 MPa) ] 2 1 2 2 2 σ r4 = − + + − + + − + , 17.3 MPa [ ] = < σ t ,安全。 (3) 10MPa σ 1 = , 20MPa σ 2 = − , 30MPa σ 3 = − ,脆性材料的危险点处于以压应力为主 的应力状态,且许用拉应力与许用压应力不等,宜采用莫尔强度理论,即: ( 30MPa) 20MPa [ ] 90MPa 30MPa 10MPa [ ] [ ] 3 t c t rM 1 σ σ σ σ σ = σ − ⋅ = − − = < ,安全 2 图示实心圆轴受轴向外力 F 和外力偶 M 作用。已知圆轴直径 d=10 mm,M=Fd/10。(1) 材料为钢时,许用应力[σ ] =160 MPa ;材料为铸铁时,许用应力[ ] 30 MPa σ t = 。试分别计算 圆轴的许可载荷[F];(2)材料为铸铁,且 F=2 kN、E=100 GPa、 µ = 0.25 ,计算圆轴表面 上与轴线成 30°方位上的正应变。 1

题2图 解题分析:本题中,轴为拉伸和扭转组合变形。轴的各个横截面上的扭矩、轴力均相同,所 以可以任取一截面作为危险截面。在危险截面上,轴力引起的拉伸正应力处处相等,扭矩引 起的切应力在靠近轴外表面的各点处最大,所以危险点为靠近轴表面的各点。危险点处的应 力状态如图示。 解:1、计算危险点的主应力 轴力起的正度力。-经-行=270F 知矩引起的切应力t文=10=0509x10m 危险点处的极值应力为 =127x10'm ,27×10my+0.509×10m-F 2 2 于是主应力为01=1.45×10m2F,02=0,03=-0.179×10m2F 2、材料为钢材时,确定轴的许用载荷 根据第三强度理论,有 06=1-03=145x10m2F+0.179×104m-2F=1.63x104m2F≤[o]=160MPa 160 MPa 得门]=163x10m=9820N=9,82kN 该轴用钢材制造时,许可载荷[F]=9.82kN 3、材料为铸铁时,确定轴的许可载荷 按第一强度理论,有 ,=,=1.45x10m2F≤,J=30MP 得许可载荷【F=2kN 4、计算铸铁轴表面与轴线成30°方位上的正应变 2
F 30o M 题 2 图 解题分析:本题中,轴为拉伸和扭转组合变形。轴的各个横截面上的扭矩、轴力均相同,所 以可以任取一截面作为危险截面。在危险截面上,轴力引起的拉伸正应力处处相等,扭矩引 起的切应力在靠近轴外表面的各点处最大,所以危险点为靠近轴表面的各点。危险点处的应 力状态如图示。 解:1、计算危险点的主应力 轴力引起的正应力 F d F A F 4 2 2 N 1.27 10 m π 4 − σ = = = × 扭矩引起的切应力 F d Fd W M W T 4 2 3 p p 0.509 10 m 10π 16 − τ = = = = × 危险点处的极值应力为 2 4 2 2 4 2 4 2 min max ) (0.509 10 m ) 2 1.27 10 m ( 2 1.27 10 m F F F − − − + × × ± × σ = 于是主应力为 σ1 = 1.45×104m−2 F ,σ 2 = 0, F 4 2 3 0.179 10 m− σ = − × 2、材料为钢材时,确定轴的许用载荷 根据第三强度理论,有 1.45 10 m 0.179 10 m 1.63 10 m [ ] 160 MPa 4 2 4 2 4 2 r3 = 1 − 3 = × + × = × ≤ = − − − σ σ σ F F F σ 得 9820 N 9.82 kN 1.63 10 m 160 MPa [ ] 4 2 = = × = − F 该轴用钢材制造时,许可载荷[F] = 9.82 kN 3、材料为铸铁时,确定轴的许可载荷 按第一强度理论,有 1.45 10 m [ ] 30 MPa t 4 2 r1 = 1 = × ≤ = − σ σ F σ 得许可载荷 [F] = 2 kN 4、计算铸铁轴表面与轴线成 30°方位上的正应变 2

根据广义胡克定律公式,要计算与轴线成30°方位上的正应变,必须知道该方向的 正应力和与该方向垂直的方向上的正应力。设要计算的方位为一30°,则与其垂直的方 位为60°,首先计算一30°、60°两方位上的正应力。 与轴线平行方向上的正应力、切应力分别为 G=1.27×10m2F=1.27×10m2×2×10N=25.4MPa t=0.509×10°m2F=0.0509×10m2×2×10N=10.18MPa 于是 。.0=g+gcos2x(-30°月-sim2x(-30月 -254NP254Mcos2x-30-1018sn2x-301=2787MP 2 6=号+号c0s(2x60°)-tsin2×60°) _254ANMP+254MP0ceos2x60')-10.18 MPa sin2x60')=-247Mm 由广义胡克定律,轴表面与轴线成30°方位上的正应变为 1 8w-Eo-w-cw)10x10Mm2787Ma-025x-247MPa》=285x10- 时论:该题中正应变的计算也可以用公式。=5十+5:cos2a-'sin2a,但和上 面方法相比,要麻烦得多。 3图示钢轴有两个皮带轮A和B,两轮的直径D=1m,轮的自重Q-5kN,轴的许用应力 o]=8OMPa。试确定轴的直径d. 解题分析:本题轮轴为弯扭组合变形。首先要将所有外力向轴线上简化,并绘制内力图,以 便寻找危险截面。找到危险截面和危险点后,即可按强度条件设计轴直径。 解:1、计算轴上的载荷 取如图示坐标系,则外力偶矩 M(5-2)kN =6-2w×受-15Nm y平面支反力Fo=12.5kN, FDy=4.5 kN x平面支反力F-9.1kN,Fn-2.1kN 2、画内力图,确定危险截面
根据广义胡克定律公式,要计算与轴线成 30°方位上的正应变,必须知道该方向的 正应力和与该方向垂直的方向上的正应力。设要计算的方位为-30°,则与其垂直的方 位为 60°,首先计算-30°、60°两方位上的正应力。 与轴线平行方向上的正应力、切应力分别为 1.27 10 m 1.27 10 m 2 10 N 25.4 MPa 4 2 4 2 3 = × = × × × = − − σ F 0.509 10 m 0.0509 10 m 2 10 N 10.18 MPa 4 2 4 2 3 = × = × × × = − − τ F 于是 cos[2 ( 30 )] 10.18sin[2 ( 30 )] 27.87 MPa 2 25.4 MPa 2 25.4 MPa cos[2 ( 30 )] sin[2 ( 30 )] 2 2 30 = + × − − × − = = + × − − × − − D D D D D τ σ σ σ cos(2 60 ) 10.18 MPa sin(2 60 ) 2.47 MPa 2 25.4 MPa 2 25.4 MPa cos(2 60 ) sin(2 60 ) 2 2 60 = + × − × = − = + × − × D D D D D τ σ σ σ 由广义胡克定律,轴表面与轴线成 30°方位上的正应变为 6 30 30 60 3 (27.87 MPa 0.25 ( 2.47 MPa)) 285 10 100 10 MPa 1 ( ) 1 − − − − × − = × × ε D = σ D − µσ D = E 讨论:该题中正应变的计算也可以用公式 α γ α ε ε ε ε ε α sin 2 2 cos 2 2 2 x y x y xy − − + + = ,但和上 面方法相比,要麻烦得多。 3 图示钢轴有两个皮带轮 A 和 B,两轮的直径 D=1m,轮的自重 Q=5kN,轴的许用应力 [σ ] = 80MPa 。试确定轴的直径 d。 解题分析:本题轮轴为弯扭组合变形。首先要将所有外力向轴线上简化,并绘制内力图,以 便寻找危险截面。找到危险截面和危险点后,即可按强度条件设计轴直径。 解: 1、计算轴上的载荷 取如图示坐标系,则外力偶矩 1.5 kN m 2 1m (5 - 2) kN 2 e e (5 - 2) kN = × = ⋅ = = D M A M B xy平面支反力 FCy=12.5 kN, FDy=4.5 kN xz平面支反力 FCz=9.1 kN,FDz=2.1 kN 2、画内力图,确定危险截面 3

轴AB段的扭矩为T=15kNm(图c),弯矩M,和M.如图d、e所示。从内力图 看出,危险截面是C或B截面。分别计算C、B两截面的总弯矩: Me=√2.1×102Nm)2+1.5×102N·m) 5kN =2.58×103Nm=2.58kN-m (a) M=V1.05×102Nm)2+(225×102NmF N 300 500 00 =2.49×10'Nm=2.49kNm 比较两者大小,可知危险截面为C截面。 (b) 3、确定轴的直径 按第三强度理论设计轴的直径。直接采用 圆轴弯扭组合情况下的强度条件,得 oa-slel ☐L.5kNm 2.1 kN-m 3 -105 kN-m 2.25kN-m 32V2.58×103N-m)2+1.5×103Nm)2 π×80x10Pa =0爬4×妮3过=2hm 1.5kN-m 如果按第四强度理论设计轴的直径,则 题3图 4-M+07rs问l n0 3 ] 3 322.58x103N.m2+0.75x1.5×103N-m =71.6×10-m=71.6mm π×80×10Pa 比较可得按第三强度理论设计的轴径比按第四强度理论设计的轴径略大。 4一端固定的轴线为半圆形的正方形截面杆,受力情况如图,F=100ON,试求B和C截面 上危险点处的相当应力。 解题分析:本题为非圆截面弯扭组合变形问题。首先应找出B和C截面的危险点,并确定 危险点处的应力状态,然后计算相当应力。 解:1、计算截面有关的几何性质 杆的横截面面积A=bh=30mm×30mm=900mm2=900×106m
轴 AB 段的扭矩为 (图 c),弯矩 和 如图 d、e 所示。从内力图 看出,危险截面是 C 或 B 截面。分别计算 C、B 两截面的总弯矩: T = 1.5 kN ⋅m M y M z 2.58 10 N m 2.58 kN m (2.1 10 N m) (1.5 10 N m) 3 3 2 3 2 = × ⋅ = ⋅ = × ⋅ + × ⋅ M C 2.49 10 N m 2.49 kN m (1.05 10 N m) (2.25 10 N m) 3 3 2 3 2 = × ⋅ = ⋅ = × ⋅ + × ⋅ M B 比较两者大小,可知危险截面为 C 截面。 5kN 3、确定轴的直径 按第三强度理论设计轴的直径。直接采用 圆轴弯扭组合情况下的强度条件,得 [ ] 2 2 σ r3 ≤ σ + = W M T 72.4 10 m 72.4 mm π 80 10 Pa 32 (2.58 10 N m) (1.5 10 N m) π[ ] 32 3 6 3 2 3 2 3 2 2 3 = × = × × × ⋅ + × ⋅ = + ≥ − σ M T d 如果按第四强度理论设计轴的直径,则 [ ] 0.75 2 2 σ r4 ≤ σ + = W M T 71.6 10 m 71.6 mm π 80 10 Pa 32 (2.58 10 N m) 0.75 (1.5 10 N m) π[ ] 32 0.75 3 6 3 2 3 2 3 2 2 3 = × = × × × ⋅ + × × ⋅ = + ≥ − σ M T d 比较可得按第三强度理论设计的轴径比按第四强度理论设计的轴径略大。 4 一端固定的轴线为半圆形的正方形截面杆,受力情况如图,F=1000N,试求 B 和 C 截面 上危险点处的相当应力σ r3。 解题分析:本题为非圆截面弯扭组合变形问题。首先应找出 B 和 C 截面的危险点,并确定 危险点处的应力状态,然后计算相当应力。 解: 1、计算截面有关的几何性质 杆的横截面面积 2 6 2 30mm 30mm 900mm 900 10 m− A = bh = × = = × 1.5 kN·m T 1.5 kN·m 题 3 图 Mz 2.25kN·m 1.05 kN·m (c) My 2.1 kN·m B 500 (b) MeA 7kN FCy 5kN z 12kN (a) 300 500 y MeB FCz A 2kN 5kN 2kN FDy FDz C D x (d) (e) 4
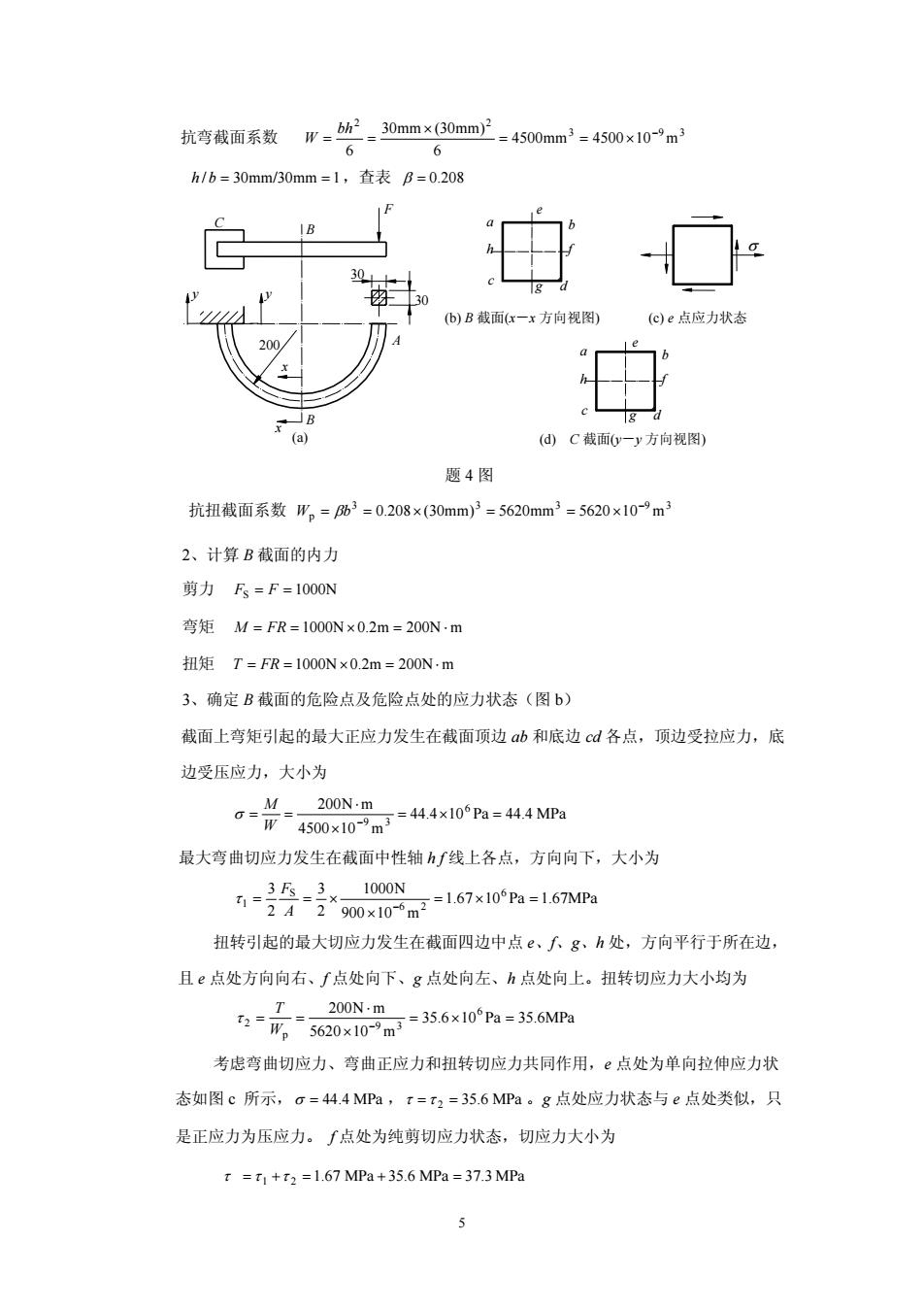
抗弯载面系数W-30mmx30mm=450m=450x10-m 0 h/b=30mm/30mm=1,查表B=0.208 30 )B载面一x方向视) (@e点应力状 (@d)C截面(一y方向视图 题4图 抗扭截面系数用。=03=0.208×(30mm)3=5620mm3=5620×109m3 2、计算B截面的内力 剪力F=F=I00ON 弯矩M=FR=1000N×0.2m=200N·m 扭矩T=-FR=1000N×0.2m=200N,m 3、确定B截面的危险点及危险点处的应力状态(图b) 截面上弯矩引起的最大正应力发生在截面顶边ab和底边cd各点,顶边受拉应力,底 边受压应力,大小为 最大弯曲切应力发生在截面中性轴∫线上各点,方向向下,大小为 有-0。=167wn16nNm 扭转引起的最大切应力发生在截面四边中点,人g、h处,方向平行于所在边, 且点处方向向右、∫点处向下、g点处向左、h点处向上。扭转切应力大小均为 -3620x10m-356x10Pm=356MP 200N,m 考虑弯曲切应力、弯曲正应力和扭转切应力共同作用,©点处为单向拉伸应力状 态如图c所示,σ=44.4MPa,t=t2=35.6MPa。g点处应力状态与e点处类似,只 是正应力为压应力。∫点处为纯剪切应力状态,切应力大小为 t=t1+r2=1.67MPa+35.6MPa=373MPa
抗弯截面系数 3 9 3 2 2 4500mm 4500 10 m 6 30mm (30mm) 6 − = = × × = = bh W h / b = 30mm/30mm = 1,查表 β = 0.208 抗扭截面系数 p 8 (30mm 5620mm 5620 10 m− W = × = = × 2 内力 3 3 3 9 3 βb = 0.20 ) 、计算 B 截面的 剪力 FS = F = 1000N 弯矩 M = FR = 1000N × 0.2m = 200N ⋅ m 扭矩 T = FR = 1000N × 0.2m = 200N ⋅ m B 截面的危险点及危险点处的应力状态(图 b) cd 各点,顶边受拉应力,底 3、确定 截面上弯矩引起的最大正应力发生在截面顶边 ab 和底边 边受压应力,大小为 44.4 10 Pa 44.4 MPa 4500 10 m 200N m = = M σ 6 9 3 = × = × ⋅ W − 最大弯曲切应力发生在截面中性轴 h f 线上各点,方向向下,大小为 1.67 10 Pa 1.67MPa 3 3 1000N 6 6 2 S 1 = = × = × = − F τ 2 A 2 900×10 m 扭转引起的最大切应力发生在截面四边中点 e、f、g、h 处,方向平行于所在边, 且 e 点处方向向右、f 点处向下、g 点处向左、h 点处向上。扭转切应力大小均为 35.6 10 Pa 35.6MPa 200N m 6 9 3 2 = × = ⋅ = = − T τ Wp 5620×10 m 考虑弯曲切应力、弯曲正应力和扭转切应力共同作用,e 点处为单向拉伸应力状 态如图 c 所示,σ = 44.4 MPa , 35.6 MPa τ = τ 2 = 。g 点处应力状态与 e 点处类似,只 是正应力为压应力 纯剪 应力大小为 1.67 MPa 35.6 MPa 37.3 MPa 1 2 。 f 点处为 切应力状态,切 τ = τ +τ = + = 30 30 B 200 B F C A e a 题 4 图 b h f σ c g d a e b h f d c g (b) B 截面(x-x 方向视图) (c) e 点应力状态 y y x ( x a) (d) C 截面(y-y 方向视图) 5

h点处应力状态也为纯剪切,切应力大小为 r=t,-t,=356MPa-1.67MPa=33.93MPa. 比较四点处的应力状态,可知点为B截面的危险点。按第三强度理论计算其相当应 力为 G3=VG2+4r2=44.4MPa)2+4x35.6MPa2=83.9MP 4、计算C截面上内力和应力 剪力F=F=1000N 弯矩0 扭矩T=2FR=2x×1000N×0.2m=400N.m 5、计算C截面危险点的应力(图d) C截面各点处均为纯剪切应力状态,最大切应力发生在C截面轴内侧中点,即图。 中∫点处,其值为 m普+深-号治 ”2g60-n9aifn-nwm 1000N 按第三强度理论计算相当应力 G =vG2+4r2 =4r2 =2rm =2x72.9MPa =145.8MPa 5图示薄壁容器承受内压P。在容器外表面沿平行于轴向贴电阻应变片A,测得 64=100x106,在垂直于轴向贴电阻应变片B,测得EB=350×106。已知制成容器材料的 弹性横量E=200GPa,μ=0.25,试计算筒壁内轴向及周向应力,并确定内压P 题5图 解题分析:本题为薄壁压力容器问题。己知筒壁一点处的轴向和周向正应变,可由广义胡克 定律计算出轴向和周向正应力,然后直接应用教材中给出的压力容器的公式计算内压P
h 点处应力状态也为纯剪切,切应力大小为 35.6 MPa -1.67 MPa 33.93 MPa τ = τ 2 −τ 1 = = 。 比较四点处的应力状态,可知 e 点为 B 截面的危险点。按第三强度理论计算其相当应 力为 4 (44.4 MPa) 4 (35.6 MPa) 83.9 MPa 2 2 2 2 σ r3 = σ + τ = + × = 4、计算 C 截面上内力和应力 剪力 F = F = =0 扭矩 S 1000N 弯矩 M 2FR = 2×1000N × 0.2m = 400N ⋅ m 5、计算 截面危险点的应力(图 d) C 截面轴内侧中点,即图 d 中 值为 T = C C 截面各点处均为纯剪切应力状态,最大切应力发生在 f 点处,其 ) 72.9 10 Pa 72.9MPa 0.208 30 10 m 2 200 10 m 2 3 ( (30 10 m) 1000N ) 2 2 3 ( 2 2 3 2 3 S max = F τ 6 3 3 3 2 2 2 p = × = × × × × + × = + = + = + − − − b R b F b FR A F W T A β β 按第三强度理论计算相当应力 4 4 2 2 72.9MPa 145.8MPa 2 max 2 2 σ r3 = σ + τ = τ = τ max = × = 5 图示薄壁容器承受内压 p。在容器外表面沿平行于轴向贴电阻应变片 A,测得 弹性模量 E=2 -6 = 100 ×10 A ε ,在垂直于轴向贴电阻应变片 B,测得 = 350 ×10 B ε 。已知制成容器材料的 00 GPa, = 0.25 -6 µ ,试计算筒壁内轴向及周向应力,并确定内压 p。 解题分析: 一点处的轴向和周 正应变,可由广义胡克 定律计算出轴向和周向正应力,然后直接应用教材中给出的压力容器的公式计算内压 p。 题 5 图 A B p 10 500 本题为薄壁压力容器问题。已知筒壁 向 6

解:1、计算出轴向和周向正应力 为计算方便,在测点处建立坐标系。设轴向为x轴,y轴为测点沿圆周的切线方 向,则A应变片测出的是轴向正应变,B片测出的是该点处周向正应变。即 6,=64=1×104,c,=eg=3.5×101 由平面应力状态下的广义胡克定律,得 0,-,+82_20x103MPmx025×350+100x10 40MPa(轴向正应力) 1-4 1-0.252 g,-2.2000251+300-M周正度》 1-4 1人0.25 2、求内压p 根据公式,-片(或,=公),可确定内压 p=g5_4x40x10x0x103m-32Nm 500×10-3m 6一个内半径为”,两端封闭的圆柱形薄壁压力容器,由厚度为6、宽度为b的板条滚压成 螺旋状并焊接而成(图a。假设焊口处的强度条件为:正应力。不得超过0.7G,和切应力r不 得超过0.501,。,为筒壁上一点处的最大正应力。为满足上述强度要求,试确定半径r和板 条的宽度b之间应满足的关系 b) (c) 题6图 解题分析:在焊口处截取微体,则焊缝为微体的斜截面。计算该斜截面上的正应力和切应力, 使其满足给定的强度条件,并由强度条件确定b与r的关系。 解:1、计算焊接面上的正应力和切应力 取微体如图所示,根据薄壁压力容器筒壁任一点处的应力状态特点,可知轴向正应 力为σ,周向正应力为口,且0,为最大。设焊缝切向与轴向夹角为a,亦即斜截面 (焊缝)法向与轴向夹角。于是得焊接面上的应力为 7
解:1、计算出轴向和周向正应力 为计算方便,在测点处建立坐标系。设轴向为 x 轴, y 轴为测点沿圆周的切线方 向,则 A 应变片测出的是轴向正应变,B 片测出的是该点处周向正应变。即 由平面应力状态下的广义胡克定律,得 -4 = =1×10 x A ε ε , -4 ε y = ε B = 3.5×10 40MPa 1 1 0.25 2 − µ − ( ) 200 10 MPa (0.25 350 100) 10 2 3 -6 = × × × + × = + = µε ε σ y x x E (轴向正应力) 80MPa 1 0.25 200 10 MPa (0.25 100 350) 10 1 ( ) 2 3 -6 2 = − × × × + × = − + = µ µε ε σ x y y E (周向正应力) 2、求内压 p 根据公式 δ σ 4 pD x = (或 δ σ 2 pD y = ),可确定内压 3.2MPa 500 10 m (4 40 10 Pa) (10 10 m) 3 6 3 = × × × × × = = − − D p δ 6 一个内半径为 r,两端封闭的圆柱形薄壁压力容器,由厚度为 4σ x δ 、宽度为 b 的板条滚压成 螺旋状并焊接而成(图 a)。假设焊口处的强度条件为:正应力σ 不得超过 7 1 0. σ 和切应力τ 不 得超过 5 1 0. σ ,σ 1为筒壁上一点处的最大正应力。为满足上述强度要求,试确定半径 r 和板 条的宽度 b 之间应满足的关系。 解题分析:在焊口处截取微体,则焊缝为微体的斜截面。计算该斜截面上的正应力和切应力, 使其满足给定的强度条件,并由强度条件 与 r 的关系 。 状态特点,可知轴向正应 确定 b 解:1、计算焊接面上的正应力和切应力 取微体如图所示,根据薄壁压力容器筒壁任一点处的应力 力为σ 2 ,周向正应力为σ 1 ,且σ 1 为最大。设焊缝切向与轴向夹角为α ,亦即斜截面 (焊缝)法向与轴向夹角。于是得焊接面上的应力为 (a) (b) ( σα c) σ2 α α 2 πr σ1 τα b b 题 6 图 7

o-0-01cs2a,=0sm2a,其中G-g 2、利用强度条件确定b与r应满足的关系 根据题中给出的强度条件,有 a=o,0,cos2a≤07oi.=0sn2a≤05a, 由第一式得cos2a≥0.2或a≤39.2°,由第二式得a可以为任何角度。所以,最后确 定取a≤39.2°。 由图e的几何关系知caCm-下,于是有 2” 2m-6之cos392或b≤3.97e4r 2ar 讨论:由确定α角的过程可知,无论《为何值,焊缝处切应力强度条件始终满足 过5%,仍然安全
σ σ cos 2α 3 1 σ α = 1 − 1 , 4 4 τ α σ sin 2α 1 1 ,其中 4 = δ σ pr 1 = 2、利用强度条件确定 b 与 r 应满足的关系 根据题中给出的强度条件,有 1 1 1 cos 2 0.7 4 4 σ α = σ − σ α ≤ σ , 3 1 1 1 sin 2 0.5 4 1 τ α = σ α ≤ σ 由第一式得cos 2α ≥ 0.2或α ≤ 39. D 2 ,由第二式得α 可以为任何角度。所以,最后确 定取 何关系知 D α ≤ 39.2 。 由图 c 的几 r πr) b cos 2 2 − ,于是有 2π (2 α = D cos 39.2 2πr (2π ) 2 2 ≥ r − b 或 b≤3.97r≈4r 讨论: 由确定α 角的过程可知,无论α 为何值,焊缝处切应力强度条件始终满足。 过 5%,仍然安全。 8