新疆大学：《材料力学》课程教学资源（PPT课件）第八章 应力与应变分析（不含视频演示）

第章应力发变状态分折 ⊙嘉面人善

第八章 应力应变状态分析

第章爱力寇变状态分析 §8-1引言 §8-2平面应力状态应力分析 §8-3应力圆 §8-4极值应力与主应力 §8-5复杂应力状态的最大应力 §8-6平面应变状态应变分析 §8-7广义胡克定律 百嘉大票

第八章 应力应变状态分析 §8-1 引言 §8-2 平面应力状态应力分析 §8-3 应力圆 §8-4 极值应力与主应力 §8-6 平面应变状态应变分析 §8-7 广义胡克定律 §8-5 复杂应力状态的最大应力

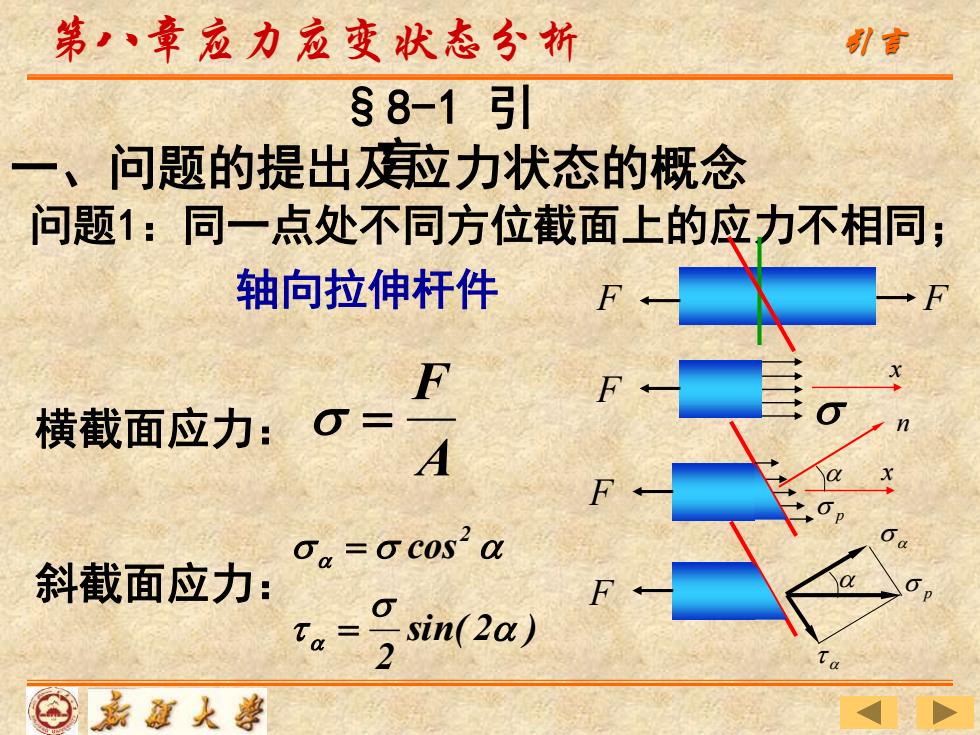
第章应力应变状态分析 引言 §8-1引 一、问题的提出应力状态的概念 问题1：同一点处不同方位截面上的应力不相同； 轴向拉伸杆件 F F F 横截面应力：O= A F a=o cos2a 斜截面应力： ta-sin(2a)

A F  = 轴向拉伸杆件 F F F  p x n  F  p      sin( 2 ) 2 cos 2         = = 斜截面应力： 问题1：同一点处不同方位截面上的应力不相同； 横截面应力： 一、问题的提出及应力状态的概念 F  x §8-1 引 言 第八章应力应变状态分析 引言

第，、章应力应变状态分析 引言 问题2：斜截面的应力是否需要研究？ 低碳钢拉 铸铁拉 ⊙嘉大兽

第八章应力应变状态分析 低碳钢拉 铸铁拉 问题2：斜截面的应力是否需要研究？ 引言

第，八章应力应变状态分析 引言 低碳钢扭 铸铁扭 需要研究斜截面的应力 ⊙嘉面人￥

第八章应力应变状态分析 低碳钢扭 铸铁扭 需要研究斜截面的应力 引言

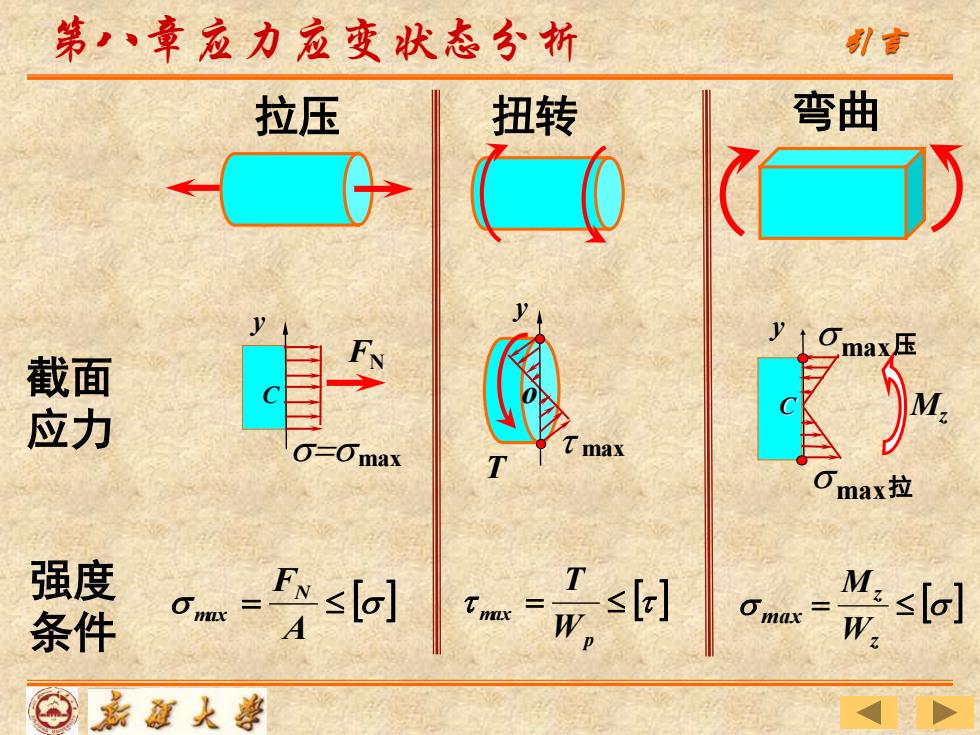
第，、章应力应变状态分析 引言 拉压 扭转 弯曲 ma 截面 应力 =Omax max max拉 强度 条件 -问 st] M:slo] W ⊙嘉道大事

拉压 扭转 弯曲 FN y = max 截面 C 应力 强度 条件  =    A FN max  =    p max W T  =    z z max W M y  max压  max拉 C Mz y  max o T 第八章应力应变状态分析 引言

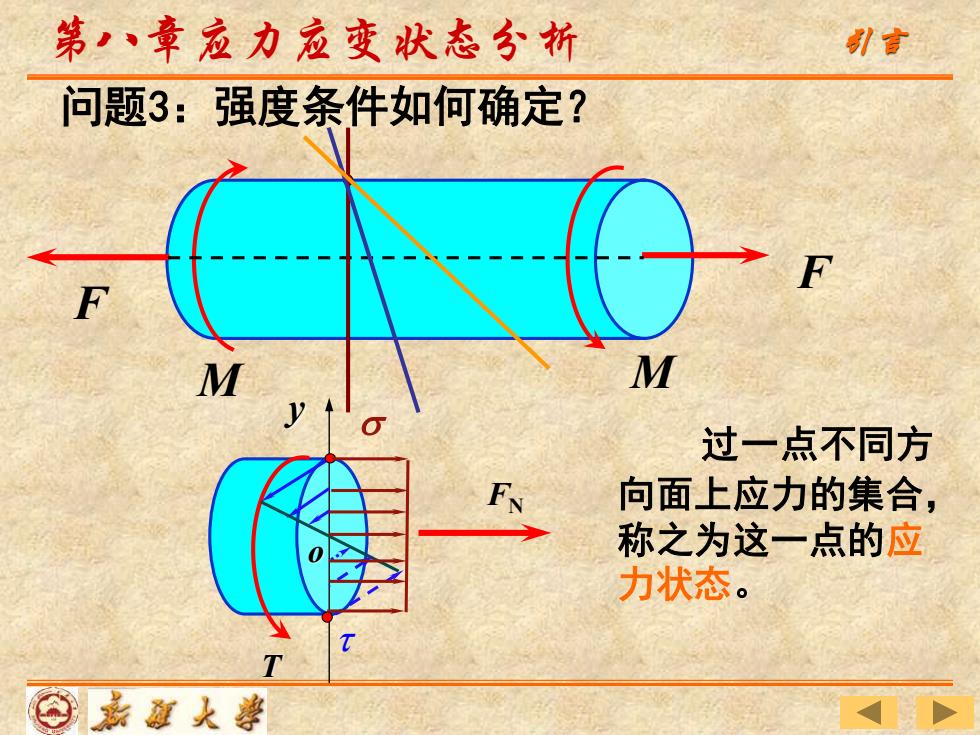
第，章应力应变状态分析 引言 问题3：强度条件如何确定？ M M 过一点不同方 F 向面上应力的集合， 称之为这一点的应 力状态。 ⊙嘉面人善

M M F F 问题3：强度条件如何确定？ y T FN o   过一点不同方 向面上应力的集合， 称之为这一点的应 力状态。 第八章应力应变状态分析 引言

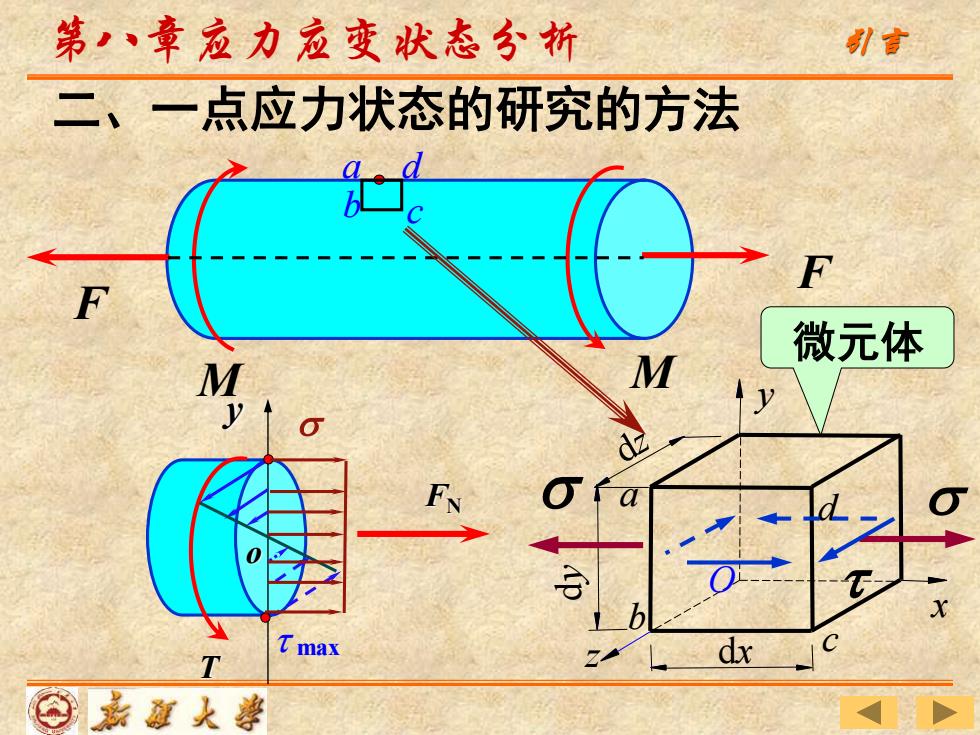
第，、章应力应变状态分析 引言 二、一点应力状态的研究的方法 微元体 M M T Tmax dx ⊙嘉道大導

M M F F y T FN o  max  二、一点应力状态的研究的方法 x y z a b O c d dx dy a b d c    微元体 第八章应力应变状态分析 引言

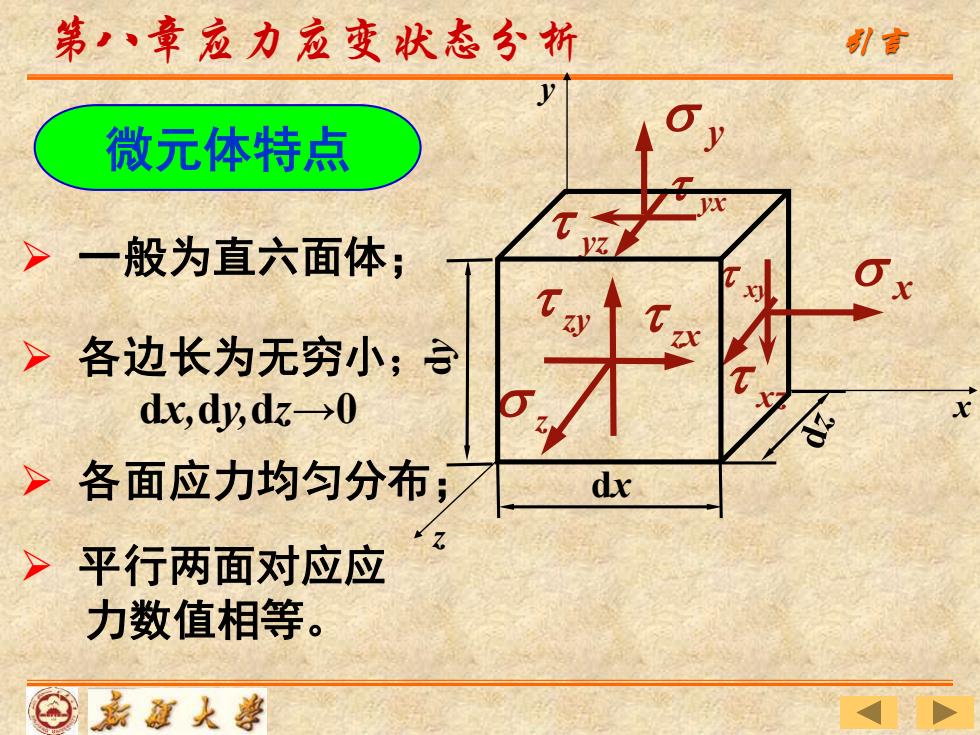
第，、章应力应变状态分析 引言 微元体特点 >一般为直六面体； >各边长为无穷小； dx,dy,dz→0 >各面应力均匀分布； dx >平行两面对应应 力数值相等。 ⊙嘉题火導

➢ 平行两面对应应 力数值相等。 ➢ 各面应力均匀分布； ➢ 各边长为无穷小； dx,dy,dz→0 ➢ 一般为直六面体； 第八章应力应变状态分析 引言 微元体特点  z  xy  yx yz  zy  xz  zx  z x y dx dy  x  y

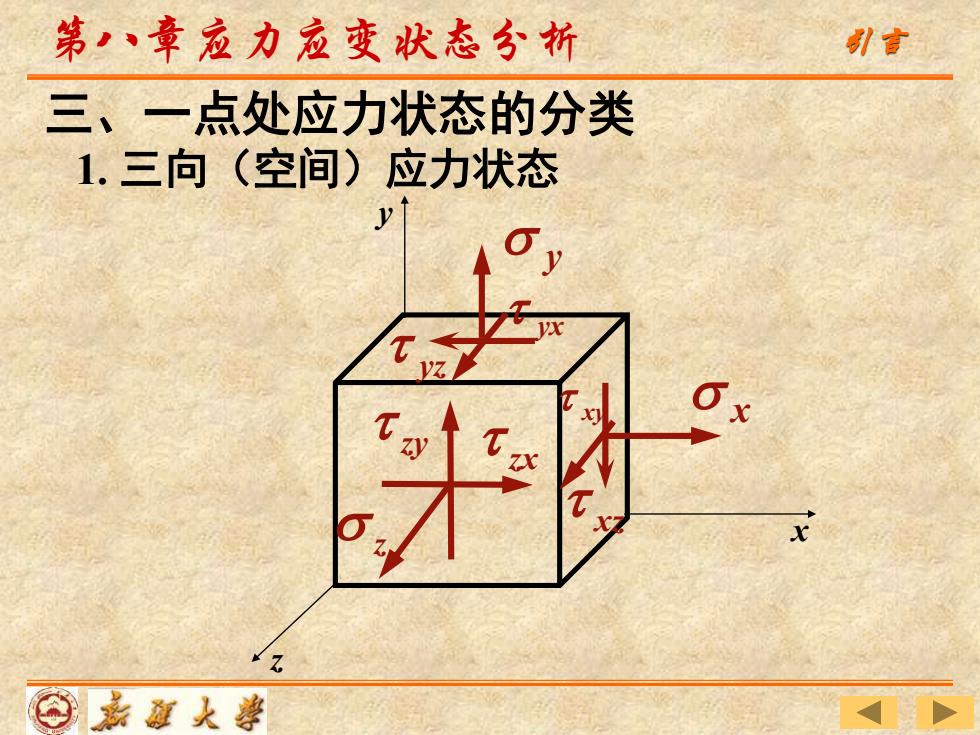
第八章应力应变状态分析 引言 三、一点处应力状态的分类 1.三向（空间）应力状态 y ⊙嘉道大事

1. 三向（空间）应力状态 三、一点处应力状态的分类 第八章应力应变状态分析 引言 z x y  x  y  z  xy  yx yz  zy  xz  zx 