《结构力学》课程教学资源（教案讲义）第七章 力法

第七章力法 本章主要内容 1)超静定结构的超静定次数 2)力法的解题思路和力法典型方程（显然力法方程中所有的系数和自由项都是指静定 基本结构的位移，可以由上一章的求位移方法求出（图乘或积分）) 3)力法的解题步骤以及用于求解超静定梁刚架桁架组合结构（排架） 4)力法的对称性利用问题，对称结构的有关概念四点结论 5)超静定结构的位移计算和最后内力图的校核 §7-1超静定结构概述 一、静力解答特征： 静定结构：由平衡条件求出支反力及内力： 超静定结构的静力特征是具有多余力，仅由静力平衡条件无法求出它的全部（有时部分 可求)反力及内力，须借助位移条件（补充方程，解答的唯一性定理）。 二、几何组成特征：（结合例题说明 静定结构：无多余联系的几何不变体 超静定结构：去掉其某一个或某几个联系（内或外），仍然可以是一个几何不变体系， 如桁架。即：超静定结构的组成特征是其具有多余联系，多余联系可以是外部的，也可 能是内部的，去掉后不改变几何不变性。 多余联系（约束）：并不是没有用的，在结构作用或调整结构的内力、位移时需要的， 减小弯矩及位移，便于应力分布均匀。 多余求知力：多余联系中产生的力称为 三、超静定结构的类型（五种） 超静定梁、超静定刚刚架、超静定桁架、超静定拱、超静定组合结构 四、超静定结构的解法 综合考虑三个方面的条件： 1、平衡条件：即结构的整体及任何一部分的受力状态都应满足平衡方程： 2、几何条件：也称变形条件、位移条件、协调条件、相容条件等。即结构的变形必须 符合支承约束条件（边界条件）和各部分之间的变形连续条件。 3、物理条件：即变形或位移与内力之间的物理关系。 精确方法： 力法（柔度法）：以多余未知力为基本未知量 位移法（刚度法）：以位移为基本未知量。 力法与位移法的联合应用： 力法与位移法的混合使用：混合法 近似方法： 力矩分配法、矩阵位移法、分层总和法、D值法、反弯点法等

1 第七章 力 法 本章主要内容 1）超静定结构的超静定次数 2）力法的解题思路和力法典型方程（显然力法方程中所有的系数和自由项都是指静定 基本结构的位移，可以由上一章的求位移方法求出（图乘或积分）） 3）力法的解题步骤以及用于求解超静定梁刚架桁架组合结构（排架） 4）力法的对称性利用问题，对称结构的有关概念四点结论 5）超静定结构的位移计算和最后内力图的校核 §7-1 超静定结构概述 一、静力解答特征： 静定结构：由平衡条件求出支反力及内力； 超静定结构的静力特征是具有多余力，仅由静力平衡条件无法求出它的全部（有时部分 可求）反力及内力，须借助位移条件（补充方程，解答的唯一性定理）。 二、几何组成特征：（结合例题说明） 静定结构：无多余联系的几何不变体 超静定结构：去掉其某一个或某几个联系（内或外），仍然可以是一个几何不变体系， 如桁架。即：超静定结构的组成特征是其具有多余联系，多余联系可以是外部的，也可 能是内部的，去掉后不改变几何不变性。 多余联系（约束）：并不是没有用的，在结构作用或调整结构的内力、位移时需要的， 减小弯矩及位移，便于应力分布均匀。 多余求知力：多余联系中产生的力称为 三、超静定结构的类型（五种） 超静定梁、超静定刚刚架、超静定桁架、超静定拱、超静定组合结构 四、超静定结构的解法 综合考虑三个方面的条件： 1、平衡条件：即结构的整体及任何一部分的受力状态都应满足平衡方程； 2、几何条件：也称变形条件、位移条件、协调条件、相容条件等。即结构的变形必须 符合支承约束条件（边界条件）和各部分之间的变形连续条件。 3、物理条件：即变形或位移与内力之间的物理关系。 精确方法： 力法（柔度法）：以多余未知力为基本未知量 位移法（刚度法）：以位移为基本未知量。 力法与位移法的联合应用： 力法与位移法的混合使用：混合法 近似方法： 力矩分配法、矩阵位移法、分层总和法、D 值法、反弯点法等

本章主要讲力法。 五、力法的解题思路（结合例子） 把不会算的超静定结构通过会算的基本结构来计算。(1)选基本结构：(2)消除基本结 构与原结构之间的差别力法： 撤除原结构的所有的多余联系，用相应的多余力代替（两者等效），得到一个静定的结 构（基本结构），基本结构在外力和多余力共同作用下保持受力和变形与原结构协调， 也就是在解除约束处的位移和原结构保持一致，列出相应的位移方程（由叠加方法）， 由此解出相应的多余力，以后的计算和内力图的作法（叠加出M图）同静定结构。 六、超静定次数n的确定 、超静定次数： =多余联系（约束）的数目=多余未知力的数目 二、确定方法：解除多余约束，使超静定结构成为几何不变的静定结构，去掉约束的数 日=n 去掉约束的方法：（结合例子说明） 1、去掉可动铰： 1 固定端一固定铰： 刚结点一单铰： 固定铰一可动铰 切晰一链杆： 2、去掉一固定铰： 固定端一可动铰： 去掉一单较： 3、去掉一固定端： 3 切断一梁式杆： 注：1、多余约束力可以多在结构内部，也可以多在结构的外部 2、同一结构中去掉约束的方式很多，但n是一定的：基本结构不是唯一的 3、把所有多余联系均拆除（内部和外部的所有的多余联系） 4、超静定结构→静定结构（多种方法，多种形式）。但不能拆成可变或瞬变，也就是结 构中有些联系不能去除（必要联系）

2 本章主要讲力法。 五、力法的解题思路（结合例子） 把不会算的超静定结构通过会算的基本结构来计算。（1）选基本结构；（2）消除基本结 构与原结构之间的差别力法： 撤除原结构的所有的多余联系，用相应的多余力代替（两者等效），得到一个静定的结 构（基本结构），基本结构在外力和多余力共同作用下保持受力和变形与原结构协调， 也就是在解除约束处的位移和原结构保持一致，列出相应的位移方程（由叠加方法）， 由此解出相应的多余力，以后的计算和内力图的作法（叠加出 M 图）同静定结构。 六、超静定次数 n 的确定 一、超静定次数： =多余联系（约束）的数目＝多余未知力的数目 二、确定方法：解除多余约束，使超静定结构成为几何不变的静定结构，去掉约束的数 目＝n 去掉约束的方法：（结合例子说明） 1、去掉可动铰： 1 固定端－固定铰： 刚结点－单铰： 固定铰－可动铰： 切断一链杆： 2、去掉一固定铰： 2 固定端－可动铰： 去掉一单铰： 3、去掉一固定端： 3 切断一梁式杆： 注：1、多余约束力可以多在结构内部，也可以多在结构的外部 2、同一结构中去掉约束的方式很多，但 n 是一定的；基本结构不是唯一的 3、把所有多余联系均拆除（内部和外部的所有的多余联系） 4、超静定结构→静定结构（多种方法，多种形式）。但不能拆成可变或瞬变，也就是结 构中有些联系不能去除（必要联系）

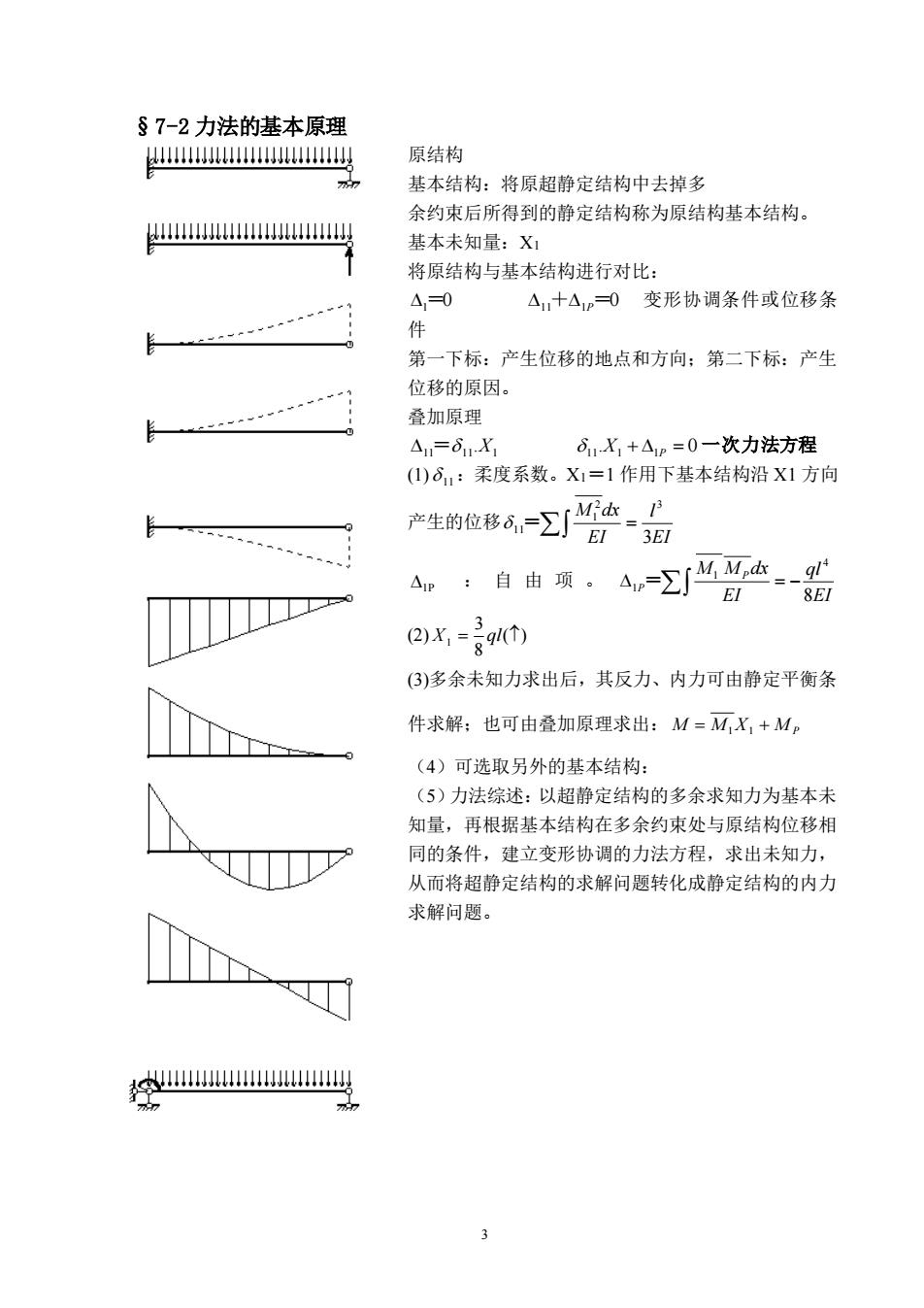
§7-2力法的基本原理 原结构 基本结构：将原超静定结构中去掉多 余约束后所得到的静定结构称为原结构基本结构。 g 基本未知量：X1 将原结构与基本结构进行对比： △，0 心 △，十△p=0变形协调条件或位移条 件 第一下标：产生位移的地点和方向：第二下标：产生 位移的原因。 叠加原理 △=6.X 6X,+△p=0一次力法方程 ()6:柔度系数。X=1作用下基本结构沿X1方向 产生的位移6，-Σ产女 2)x,=5g1t) (3)多余未知力求出后，其反力、内力可由静定平衡条 件求解：也可由叠加原理求出：M=MX,+M (4)可选取另外的基本结构： (5)力法综述：以超静定结构的多余求知力为基本未 知量，再根据基本结构在多余约束处与原结构位移相 同的条件，建立变形协调的力法方程，求出未知力， 从而将超静定结构的求解问题转化成静定结构的内力 求解问题。 空u以

3 §7-2 力法的基本原理 原结构 基本结构：将原超静定结构中去掉多 余约束后所得到的静定结构称为原结构基本结构。 基本未知量：X1 将原结构与基本结构进行对比： 1 ＝0 11＋1P ＝0 变形协调条件或位移条 件 第一下标：产生位移的地点和方向；第二下标：产生 位移的原因。 叠加原理 11 11 1  ＝ .X  11.X1 + 1P = 0 一次力法方程 (1)  11 ：柔度系数。X1＝1 作用下基本结构沿 X1 方向 产生的位移  = EI l EI M dx 3 2 3 1  11 ＝ 1P ：自由项。   = − EI ql EI M M dx P P 8 4 1 1 ＝ (2) ( ) 8 3 X1 = ql  (3)多余未知力求出后，其反力、内力可由静定平衡条 件求解；也可由叠加原理求出： M = M1X1 + M P （4）可选取另外的基本结构： （5）力法综述：以超静定结构的多余求知力为基本未 知量，再根据基本结构在多余约束处与原结构位移相 同的条件，建立变形协调的力法方程，求出未知力， 从而将超静定结构的求解问题转化成静定结构的内力 求解问题

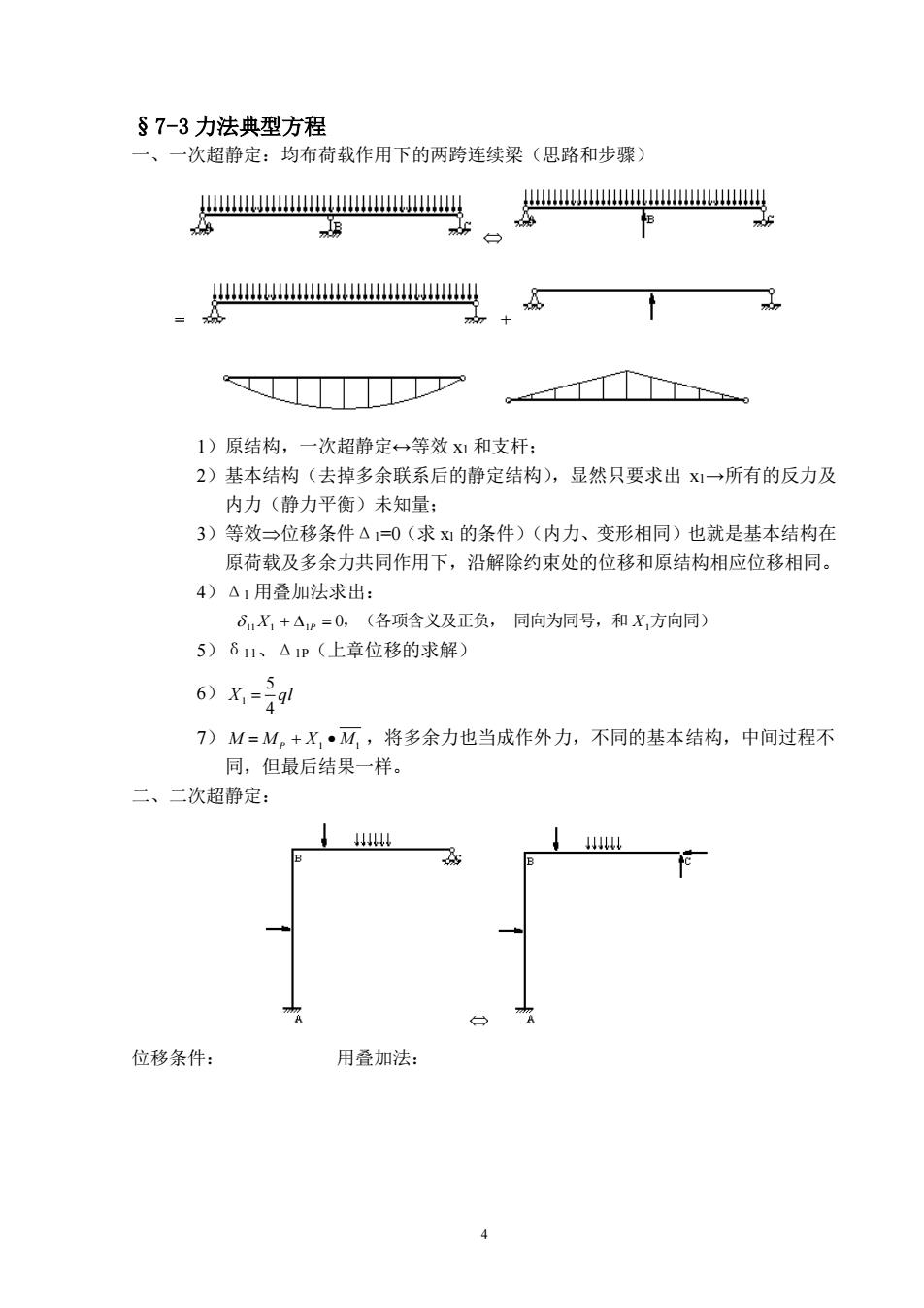
§7-3力法典型方程 一、一次超静定：均布荷载作用下的两跨连续梁（思路和步骤） 公些 ww P 。 1)原结构，一次超静定→等效x1和支杆： 2)基本结构（去掉多余联系后的静定结构），显然只要求出x1→所有的反力及 内力（静力平衡）未知量： 3)等效一位移条件△1=0（求1的条件）（内力、变形相同）也就是基本结构在 原荷载及多余力共同作用下，沿解除约束处的位移和原结构相应位移相同。 4)△1用叠加法求出： 6X,+△=0，（各项含义及正负，同向为同号，和X,方向同） 5)61、△1P(上章位移的求解) 6)x=9叫 7)M=M。+X,·M,将多余力也当成作外力，不同的基本结构，中间过程不 同，但最后结果一样。 二、二次超静定： 位移条件： 用叠加法：

4 §7-3 力法典型方程 一、一次超静定：均布荷载作用下的两跨连续梁（思路和步骤）  = + 1）原结构，一次超静定↔等效 x1 和支杆； 2）基本结构（去掉多余联系后的静定结构），显然只要求出 x1→所有的反力及 内力（静力平衡）未知量； 3）等效位移条件Δ1=0（求 x1 的条件）（内力、变形相同）也就是基本结构在 原荷载及多余力共同作用下，沿解除约束处的位移和原结构相应位移相同。 4）Δ1 用叠加法求出：  11X1 + 1P = 0，（各项含义及正负， 同向为同号，和 X1方向同） 5）δ11、Δ1P（上章位移的求解） 6） X ql 4 5 1 = 7） M M P X1 M1 = + • ，将多余力也当成作外力，不同的基本结构，中间过程不 同，但最后结果一样。 二、二次超静定：  位移条件： 用叠加法：

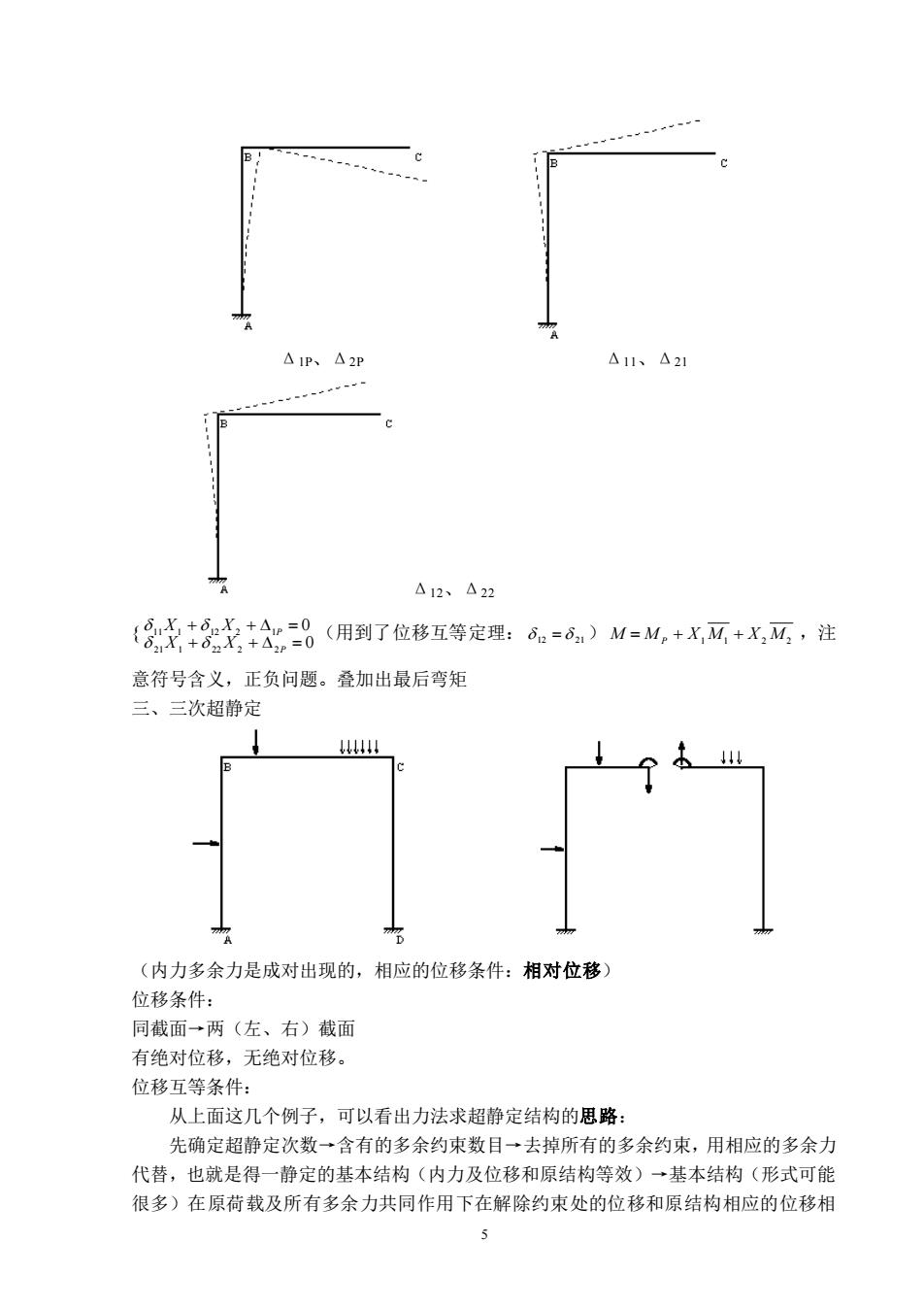
△12、△22 (爱点8点公品（用到了位移互等定理：=6）M=M,+X网+X可，注 意符号含义，正负问题。叠加出最后弯矩 三、三次超静定 (内力多余力是成对出现的，相应的位移条件：相对位移 位移条件： 同截面一两（左、右）截面 有绝对位移，无绝对位移。 位移互等条件： 从上面这几个例子，可以看出力法求超静定结构的思路： 先确定超静定次数一含有的多余约束数目→去掉所有的多余约束，用相应的多余力 代替，也就是得一静定的基本结构（内力及位移和原结构等效）→基本结构（形式可能 很多)在原荷载及所有多余力共同作用下在解除约束处的位移和原结构相应的位移相

5 Δ1P、Δ2P Δ11、Δ21 Δ12、Δ22 { 0 0 21 1 22 2 2 11 1 12 2 1 + +  = + +  = P P X X X X     （用到了位移互等定理：  12 =  21 ） M = M P + X1M1 + X2 M2 ，注 意符号含义，正负问题。叠加出最后弯矩 三、三次超静定 （内力多余力是成对出现的，相应的位移条件：相对位移） 位移条件： 同截面→两（左、右）截面 有绝对位移，无绝对位移。 位移互等条件： 从上面这几个例子，可以看出力法求超静定结构的思路： 先确定超静定次数→含有的多余约束数目→去掉所有的多余约束，用相应的多余力 代替，也就是得一静定的基本结构（内力及位移和原结构等效）→基本结构（形式可能 很多）在原荷载及所有多余力共同作用下在解除约束处的位移和原结构相应的位移相

同，得位移条件→建立补充方程→求系数及自由项（基本结构的位移计算），求出所有 多余力→由静力平衡条件和叠加法解方程求出原结构的其他反力和内力，作出最后内力 图，求位移（静定结构的计算问题），求内力。 1)先解除超静定结构的多余约束，用多余力代替，使原结构→静定的基本结构. 2)基本结构在原结构和多余力共同作用下在解除约束处的位移和原结构相应位置的位 移相同 3)由位移条件列补充方程，求出多余力。 4)多余力己知后，原结构的其他约束反力和内力及位移的计算问题变成静定结构的计 算问题。最后的弯矩图可由叠加法作出。 从上可见：由位移条件求出多余力，求出多余力以后，超静定结构的计算问题就变 成静定结构的计算问题，而求多余力，除了解方程组以外，系数和自由项的计算还是静 定结构的位移计算问题。 超静定结构的→静定结构的位移和内力计算问题。 四、力法典型方程： 推广到n次超静定结构：对于一个n次超静定结构，有n个多余约束，解除全部多余约 束，用n个多余力代替，得一个静定的基本结构一在原结构及n个多余力共同作用下， 在n个解除约束处的位移和原结构位移相同，也就是有n个位移条件得个一般方程。 6X+62X2+.+6nXn+△p=0 6mX,+62X2十+6nmXn+△np=0 上面的方程组是力法方程的一般形式，它们在组成上具有一定的规律，而不论超静 定结构的次数、类型及所选取的基本结构如何，得的方程都具有上面的形式，各项表示 的意义也相同。称为力法典型方程。 式中： 1、6：主系数。基本结构在多余未知力X=1下在自身方向上产生的位移大小。恒为 正 6-+ 2、6：副系数。基本结构在多余未知力X1下在灯j方向上产生的位移大小。可正、 负、零 A,-6,-z1"M+zx+Eg 3、△：自由项。基本结构在荷载作用下在第I个多余未知力方向上产生的位移大小。 可正、负、零 A=Σr4M+zrX+Σ8 EI EA GA 6

6 同，得位移条件→建立补充方程→求系数及自由项（基本结构的位移计算），求出所有 多余力→由静力平衡条件和叠加法解方程求出原结构的其他反力和内力，作出最后内力 图，求位移（静定结构的计算问题），求内力。 1) 先解除超静定结构的多余约束，用多余力代替，使原结构→静定的基本结构. 2) 基本结构在原结构和多余力共同作用下在解除约束处的位移和原结构相应位置的位 移相同。 3) 由位移条件列补充方程，求出多余力。 4) 多余力已知后，原结构的其他约束反力和内力及位移的计算问题变成静定结构的计 算问题。最后的弯矩图可由叠加法作出。 从上可见：由位移条件求出多余力，求出多余力以后，超静定结构的计算问题就变 成静定结构的计算问题，而求多余力，除了解方程组以外，系数和自由项的计算还是静 定结构的位移计算问题。 超静定结构的→静定结构的位移和内力计算问题。 四、力法典型方程： 推广到 n 次超静定结构：对于一个 n 次超静定结构，有 n 个多余约束，解除全部多余约 束，用 n 个多余力代替，得一个静定的基本结构在原结构及 n 个多余力共同作用下， 在 n 个解除约束处的位移和原结构位移相同，也就是有 n 个位移条件得 n 个一般方程。  11X1＋ 12X2＋＋ 1nXn + 1P ＝0  n1X1＋ n2X2＋＋ nnXn + nP ＝0 上面的方程组是力法方程的一般形式，它们在组成上具有一定的规律，而不论超静 定结构的次数、类型及所选取的基本结构如何，得的方程都具有上面的形式，各项表示 的意义也相同。称为力法典型方程。 式中： 1、 ii ：主系数。基本结构在多余未知力 Xi=1 下在自身方向上产生的位移大小。恒为 正    = + + GA Q ds u EA N ds EI M ds i i i ii 2 2 2  2、 ij ：副系数。基本结构在多余未知力 Xi=1 下在 Xj 方向上产生的位移大小。可正、 负、零    = = + + GA Q Q ds u EA N N ds EI M M ds i j i j i j  i j  j i 3、 iP ：自由项。基本结构在荷载作用下在第 I 个多余未知力方向上产生的位移大小。 可正、负、零     = + + GA Q Q ds u EA N N ds EI M M ds i P i P i P iP

五、力法求解超静定结构的步骤： 1、先判定其超静定次数，（含多余联系数），去掉原结构的所有多余联系，用相应的多 余力代替，得一静定的基本结构（形式可能很多，尽量简单）： 2、根据基本结构在原荷载及所有多余力共同作用下，在每一个去掉的多余联系处位移 和原结构相应位置的己知位移相同，建立力法典型方程： 3、求方程所有系数和自由项，（静定结构的位移计算）积分法或图乘法，写出基本结构 在单位力及原荷载分别单独作用下的内力表达式或作出内力图： 4、解方程，求出所有多余力： 5、作最后内力图（静定结构的计算问题） 梁、刚架：M=∑X,M+M。→Q一N 桁架：N=ΣX,N,+N, 组合结构： 6、校核，两方面：平衡条件（截取结构中刚结点、杆件或某一部分，应满足 ∑X=0∑Y=0∑M=0):变形协调条件（多余约束处位移是否与已知位移相等） 注：选取基本结构的原则：(1)基本结构为静定结构： (2)选取的基本结构应使力法方程中系数和自由项的计算尽可能方便，并尽量使较多 的副系数和自由项为0 (3)较易绘M图及Mr图

7 五、力法求解超静定结构的步骤： 1、先判定其超静定次数，（含多余联系数），去掉原结构的所有多余联系，用相应的多 余力代替，得一静定的基本结构（形式可能很多，尽量简单）； 2、根据基本结构在原荷载及所有多余力共同作用下，在每一个去掉的多余联系处位移 和原结构相应位置的已知位移相同，建立力法典型方程； 3、求方程所有系数和自由项，（静定结构的位移计算）积分法或图乘法，写出基本结构 在单位力及原荷载分别单独作用下的内力表达式或作出内力图； 4、解方程，求出所有多余力； 5、作最后内力图（静定结构的计算问题） 梁、刚架： M =  Xi Mi + M P→Q→N 桁架： N =  Xi Ni + NP 组合结构： 6、校核，两方面 ：平衡条件 （截取结 构中刚结 点、杆件或 某一部分 ，应满足 X＝0 Y＝0 M＝0 ）；变形协调条件（多余约束处位移是否与已知位移相等） 注：选取基本结构的原则：（1）基本结构为静定结构； （2）选取的基本结构应使力法方程中系数和自由项的计算尽可能方便，并尽量使较多 的副系数和自由项为 0 （3）较易绘 M 图及 MP 图

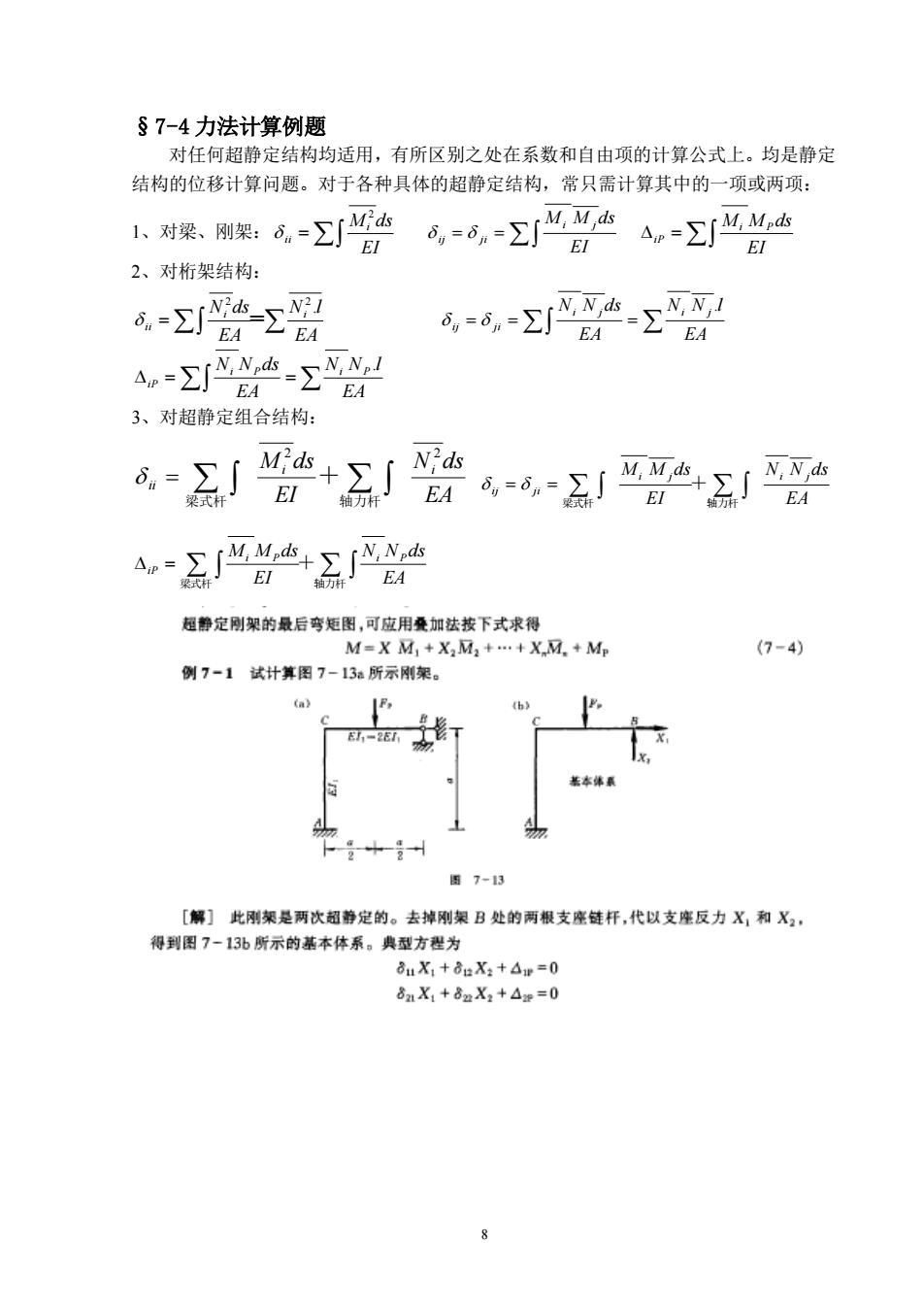
§7-4力法计算例题 对任何超静定结构均适用，有所区别之处在系数和自由项的计算公式上。均是静定 结构的位移计算问题。对于各种具体的超静定结构，常只需计算其中的一项或两项： 小对梁、附架：d-∑达G,=6,-Σ色4，-Σ4 EI EI EI 2、对桁架结构： 成-警Σ哥 A,=6,-z心x-ΣNN EA EA -Σ-Σ EA 3、对超静定组合结构： 成=引+∫。-8别 梁式杆 EI 轴方杆1 EA EA 超静定刚架的最后弯矩图，可应用叠加法按下式求得 M=XM,+X☑，+：+X☑+ (7-4 例7-1试计算图7-13所示刚架。 E,2E 图7-3 [解】此刚架是两次超静定的。去掉刚架B处的两根支座链杆，代以支座反力X,和X2: 得到图7-13b所示的基本体系。典型方型为 8uX.+8:Xa+△e=0 8mX1+6X2+4w=0

8 §7-4 力法计算例题 对任何超静定结构均适用，有所区别之处在系数和自由项的计算公式上。均是静定 结构的位移计算问题。对于各种具体的超静定结构，常只需计算其中的一项或两项： 1、对梁、刚架：  = EI M ds i ii 2   = = EI M M ds i j  ij  ji   = EI M M ds i P iP 2、对桁架结构： =   EA N l EA N ds i i ii . 2 2  ＝ = =  =  EA N N l EA N N ds i j i j ij ji .    =  =  EA N N l EA N N ds i P i P iP . 3、对超静定组合结构：     = 梁式杆 轴力杆 ＋ EA N ds EI M ds i i ii 2 2      = = 梁式杆 轴力杆 ＋ EA N N ds EI M M ds i j i j  ij  ji      = 梁式杆 轴力杆 ＋ EA N N ds EI M M ds i P i P iP

绘出各单位弯矩图和荷载弯矩图如图7-14a、b、c所示。 利用图乘法求得各系数和自由项如下： =试（号·号） a(号号）+立(aa)- a=a=武（号a0 a(修学）小- 4=应（侵学号》（婴 代人典型方程并消去员，得 号x-x+号=0 -x+x-8=0 解联立方程，得 =-品F,X= 从以上结果可以看出：在荷载作用下，多余力（进一步可 推及结构的内力)的大小只与杆件的相对刚度有关，面与其她 对刚度无关：对于同一材料所构成的结构，也与材料的性质 (弹性模量)无关 多余力求得后，最后弯矩图可按式(7一4)计算 M=X M,+XM,+M 其结果如图7-14d所示。 至于剪力图和轴力图，在本例情况下，当各多余力求出后，可 直接由图7-13动所示的基本体系作出，如图7-15，b所示。 图7-14 二、短静定粉架 由于在桁果各杆中只产生领力，故典型方程中的系数应按下列公式计算： =Σ (7-5

9

例7-2试计算图7-16：所示超静定桁架。已知各杆的材料和面面积都相同 [解】此架是一次超静定结构。现将杆12切断并代以多余力X,其基本体系如图 16仙所示。根据切口处两侧输面的相对位移应等干零的条件，可建立力法真型方程如下： &X,+4B■0 为丁计算系数和自由项，先分别求出单位多余力和荷载作用于基本结构时所产生的轴力，如 图7-16c,d所示，按式(7-5)和(7-6)计算，得 -3-高（方x4+r×2小2责2 =高-a}(-Fx2+1w,a]小-+ 代人奥型方程后求解，得 X=-=20写 原结构中各杆轴力按下式计算 Fw-FF+Fu 其结果示于图7-16e 计算时注意，显然杆2被初断，但在多余力作用下其轴力并不为零，故在的算式中必须 将与其相应的发瓷包括在内。 ☒

10