第四章静定拱 基本念 拱结构定义:杆轴线为曲线,在竖向荷载作用下,会产生水平推力的结构。水平推力的存在 与否是区别拱与梁的主要标志。 三较拱的受力特征(竖向荷载作用下):(1)三铰拱的竖向反力与相应水平间质量的竖向反 力相等,与拱轴线形状及拱高无关:(2)轴力是三较拱的主内力:(3)水平推力只与三较位 置及荷载有关, 与拱轴线无关,拱高越大,推力越小,反之,拱高越小,推力越大:(4)水 平推力的存在,使三铰拱各裁面上的弯矩比相应简支梁上的弯矩要小。 合理拱轴线定义:当拱在固定荷载作用下各截面受到均匀压力且处于无弯矩及无剪力状态, 此时的拱轴线称合理拱轴线。 部分题解 43试求图是抛物线三较拱中各链杆和截面k的内力 10N/m 田 2、 解:(1)求支反力 竖向支座反力'='g=10×9=90kN,水平支反力H4=0 (2)求二力杆轴力 ×10×182 用11截面以左为隔离体,由∑Mc=0有Ne=8 3 =135kW 去结点为隔离体,可得ND=N=136.87kNND=N=22.5W (3)求K截面的坐标及倾角 拱结方程为y一兰-到 %骨受-”网以9 9:=30'39,sing=0.5098,cosg,=0.8603
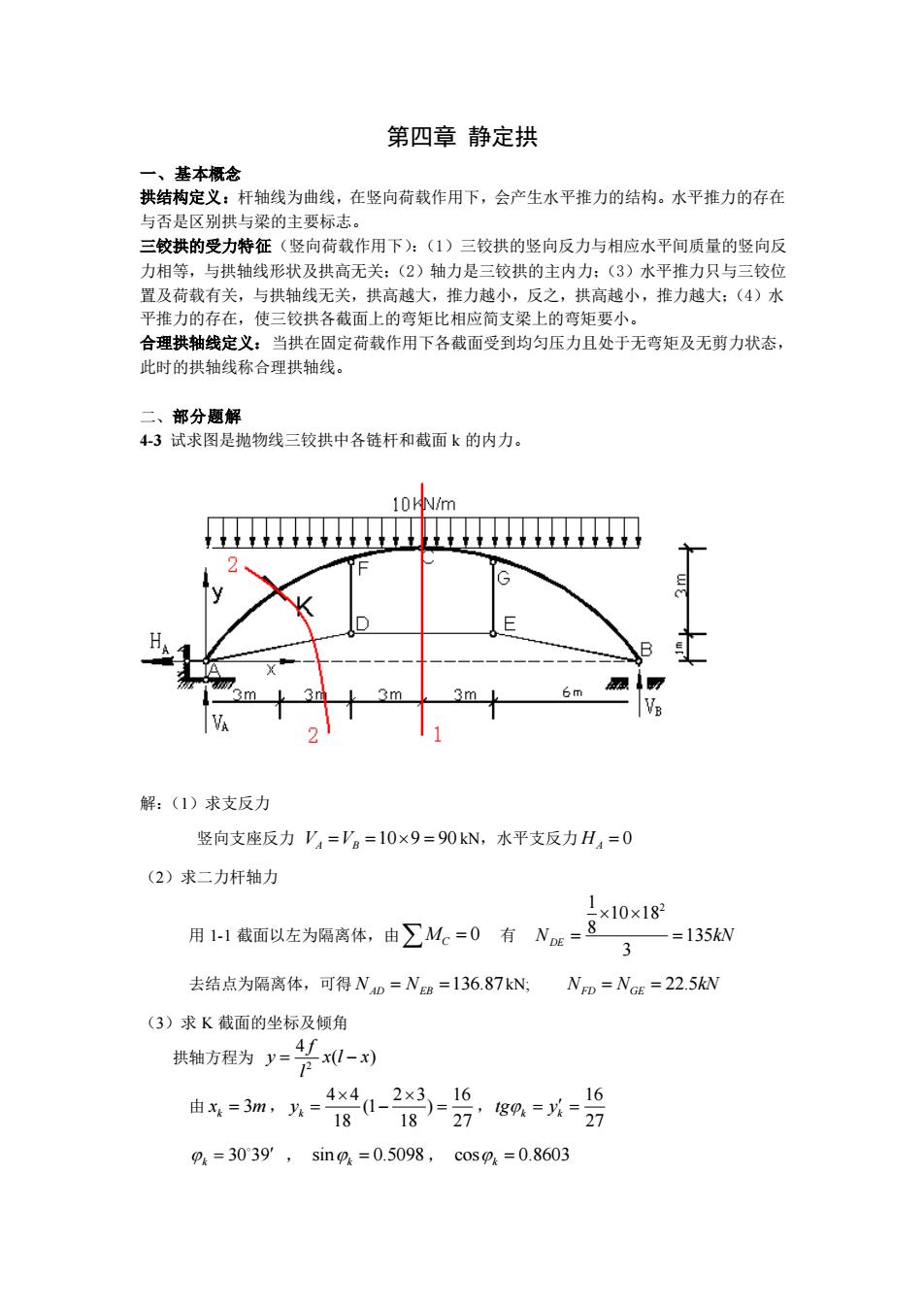
第四章 静定拱 一、基本概念 拱结构定义:杆轴线为曲线,在竖向荷载作用下,会产生水平推力的结构。水平推力的存在 与否是区别拱与梁的主要标志。 三铰拱的受力特征(竖向荷载作用下):(1)三铰拱的竖向反力与相应水平间质量的竖向反 力相等,与拱轴线形状及拱高无关;(2)轴力是三铰拱的主内力;(3)水平推力只与三铰位 置及荷载有关,与拱轴线无关,拱高越大,推力越小,反之,拱高越小,推力越大;(4)水 平推力的存在,使三铰拱各截面上的弯矩比相应简支梁上的弯矩要小。 合理拱轴线定义:当拱在固定荷载作用下各截面受到均匀压力且处于无弯矩及无剪力状态, 此时的拱轴线称合理拱轴线。 二、部分题解 4-3 试求图是抛物线三铰拱中各链杆和截面 k 的内力。 解:(1)求支反力 竖向支座反力 10 9 90 V V A B = = = kN,水平支反力 0 HA = (2)求二力杆轴力 用 1-1 截面以左为隔离体,由 0 MC = 有 1 2 10 18 8 135 3 N kN DE = = 去结点为隔离体,可得 136.87 N N AD EB = = kN; 22.5 N N kN FD GE = = (3)求 K 截面的坐标及倾角 拱轴方程为 2 4 ( ) f y x l x l = − 由 3 k x m = , 4 4 2 3 16 (1 ) 18 18 27 k y = − = , 16 27 k k tg y = = 30 39 k = , sin 0.5098 k = , cos 0.8603 k =
(4)求K截面的内力(取2-2截面以左隔离体) M=(0+2x3-×10x3-135x =-7.5Wm F=(90+22.5-10×3)×0.8603-135×0.5098=2.152k F4=(90+22.5-10×3)×0.5098+135×0.8603=158.199kW 4一4图中虚线表示一三铰拱,在均布荷载作用下试求其合理轴线方程 吲 mmmm四 H 6a 3a 解:由整体平衡和同富平衡可符支反力H-子0,么-90,上-90 按合理拱轴线条件,拱上任一截面弯矩M()=,x-92-历=0 将,=2头g如代入上式整理得合理拱轴线方程: y=21-2 4一5试求图示抛物线三较拱中截面K的内力 目 HA 10m 5M 解:(1)求支反力 取整体,由∑M,=0得'。=10.5W(个),∑F=0,得V4=-10.5W() 取AC段,由∑M=0得H=26.25W(←-):
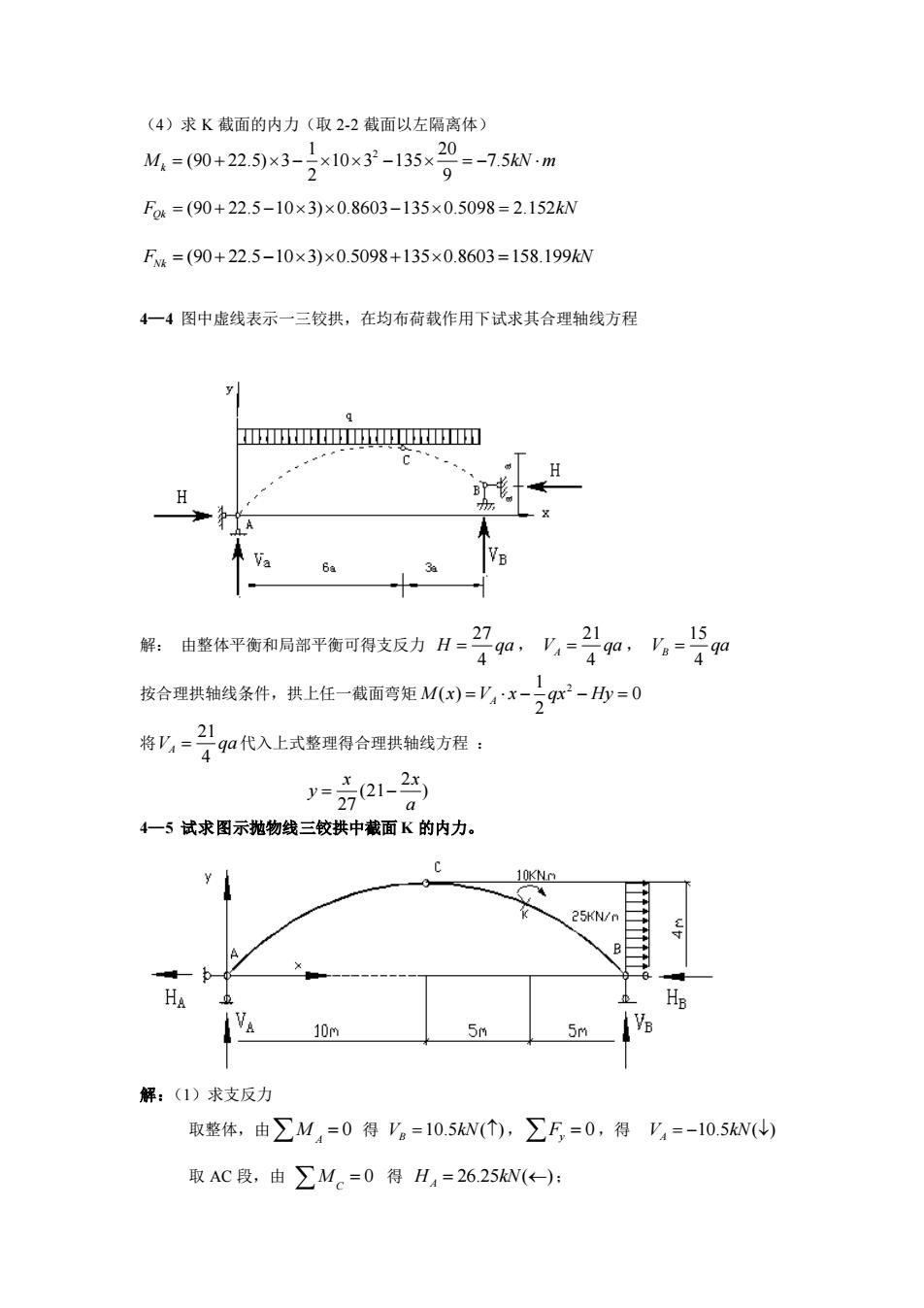
(4)求 K 截面的内力(取 2-2 截面以左隔离体) 1 20 2 (90 22.5) 3 10 3 135 7.5 2 9 M kN m k = + − − = − (90 22.5 10 3) 0.8603 135 0.5098 2.152 F kN Qk = + − − = (90 22.5 10 3) 0.5098 135 0.8603 158.199 F kN Nk = + − + = 4—4 图中虚线表示一三铰拱,在均布荷载作用下试求其合理轴线方程 解: 由整体平衡和局部平衡可得支反力 27 4 H qa = , 21 4 V qa A = , 15 4 V qa B = 按合理拱轴线条件,拱上任一截面弯矩 1 2 ( ) 0 2 M x V x qx Hy = − − = A 将 21 4 V qa A = 代入上式整理得合理拱轴线方程 : 2 (21 ) 27 x x y a = − 4—5 试求图示抛物线三铰拱中截面 K 的内力。 解:(1)求支反力 取整体,由 0 M A = 得 10.5 ( ) V kN B = , 0 F y = ,得 10.5 ( ) V kN A = − 取 AC 段,由 0 M C = 得 26.25 ( ) H kN A = ;

取整体,由∑F=0,得H。=73.75W(←-) (2)求K截面坐标及倾角 =15.%-=其0-=20-15x15=3 tang=y,0.=-21.8,sin9=0.371,cosg=0.928 (3)求K截面的内力 分别取K左至B、取K右至B求弯矩 25KN/n 25KN/n ↓5m ↓5m M=10.5x5-73,75x3+2x25x32-10=-6625wm M=105x5-7375x3+x25x3=-562wm Fx=(73.75-25×3)sin-10.5cosg=-10.21kW Fx=(73.75-25×3)cosg,+10.5sing=2.736kW
取整体,由 0 F x = , 得 73.75 ( ) H kN B = (2)求 K 截面坐标及倾角 15 K x = , 2 2 4 4 4 ( ) (20 15) 15 3 20 k f y l x x l = − = − = , tan k k = y , 21.8 k = − , sin 0.371 k = , cos 0.928 k = (3)求 K 截面的内力 分别取 K 左至 B、取 K 右至 B 求弯矩 1 2 10.5 5 73.75 3 25 3 10 66.25 . 2 zuo M kN m k = − + − = − 1 2 10.5 5 73.75 3 25 3 56.2 . 2 you M kN m k = − + = − (73.75 25 3)sin 10.5cos 10.21 F kN QK k k = − − = − (73.75 25 3)cos 10.5sin 2.736 F kN NK k k = − + =