第八章位移法 为杆系结构的有限元法, 位移法的基本结构一一单跨超静定量的组合体 位移法的基木未知量一一独立结占位移(结点角位移和线位移) 位移法的基本方程 一平衡方程 建立基本方程 方法一:直接平衡法:拆(写出杆端弯矩表达式)→搭(对每个刚结点写出结点力矩平衡方 程:对每个独立的结点线位移写截面剪力平衡方程)。 方法二:利用基本体系转化为原结构的条件建立基本方程。该方法又称典型方程法,求解过 程与力法一一对应。即: 求解基本方程一基木未知量一杆端弯矩一弯矩图 二、部分题解 8一1-8一12对于图示结构,在位移法计算中期基本未知量的数目。 一个线位移 六个角位移、三个线位移 六个角位移、两个线位移 两个线位移 五个角位移,两个线位移 两个角位移、两个线位移 四个角位移、两个线位移 两个角位移、一个线位移
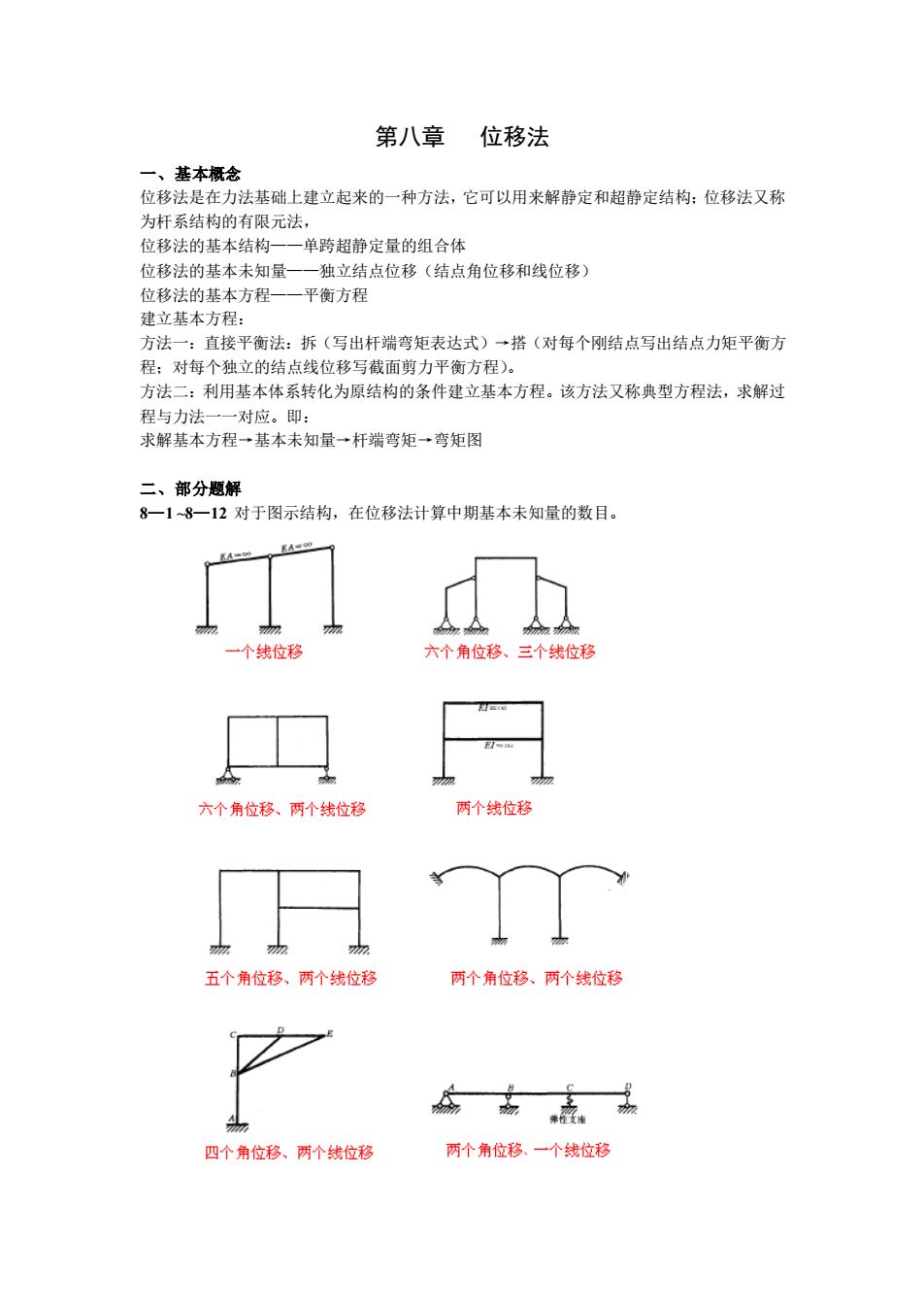
第八章 位移法 一、基本概念 位移法是在力法基础上建立起来的一种方法,它可以用来解静定和超静定结构;位移法又称 为杆系结构的有限元法, 位移法的基本结构——单跨超静定量的组合体 位移法的基本未知量——独立结点位移(结点角位移和线位移) 位移法的基本方程——平衡方程 建立基本方程: 方法一:直接平衡法:拆(写出杆端弯矩表达式)→搭(对每个刚结点写出结点力矩平衡方 程;对每个独立的结点线位移写截面剪力平衡方程)。 方法二:利用基本体系转化为原结构的条件建立基本方程。该方法又称典型方程法,求解过 程与力法一一对应。即: 求解基本方程→基本未知量→杆端弯矩→弯矩图 二、部分题解 8—1 ~8—12 对于图示结构,在位移法计算中期基本未知量的数目

两个角位移,两个线位移 两个角位 6髻 两个角位移 一个角位移 8一15用位移法计算图示刚架 山恤出 30 kN/M 21 c21 0 B 4m 4m 4m 4m 解:(1)基本未知量:结点C的转角Z,和结点D的转角Z2 (2)写出杆端弯矩表达式 4 Me-4xE Me=2x号2 Mc-2x29名+422 4 Mm=4县Z Mor =4x 2El 1 24Z-立×30×4 Mn-2x22,+304 4 (3)列平衡方程 McD +Mca =0 321+Z2=0 Moc Mpa MDE =0 +5品智0 精:名=沿 名= (④)杆端弯矩
8—15 用位移法计算图示刚架 A B C D E 30kN/m I I 2I 2I 4m 4m 4m 30 k N/ M 2I 2I I I A B 4 m 4 m 4m C D E Z1 Z2 解:(1)基本未知量:结点 C 的转角 Z1 和结点 D 的转角 Z2 (2)写出杆端弯矩表达式 1 2 4 2 2 4 2 4 Z EI Z EI MCD = + 1 4 4 Z EI MCA = 1 4 2 Z EI M AC = 1 2 4 2 4 4 2 2 Z EI Z EI M DC = + 2 4 4 Z EI M DB = 2 2 30 4 12 1 4 2 = 4 Z − EI M DE 2 4 2 Z EI M BD = 2 2 30 4 12 1 4 2 = 2 Z + EI M ED (3)列平衡方程 MCD + MCA = 0 3Z1 + Z2 = 0 MDC + M DB + M DE = 0 0 40 1 + 5 2 − = EI Z Z 解得: EI Z 7 20 1 = − EI Z 7 60 2 = (4) 杆端弯矩
Mcp =2.86KN.m Mpc =14.29KN.m Mc4=-2.86KN.m Mc=-1.43KN.m Mpe =8.57KN.m MD=4.29KN·m Mpe =-22.86KN.m MEp =48.57KN.m 48.57 22.86 一不一 14.29 60 2.86 2.86 8.57D 1.48 4.9 (单位:KN0 819用位移法计算图示刚架 40kN 入 解:(1)基本未知量:结点D的转角Z,和结点E的水平位移Z2
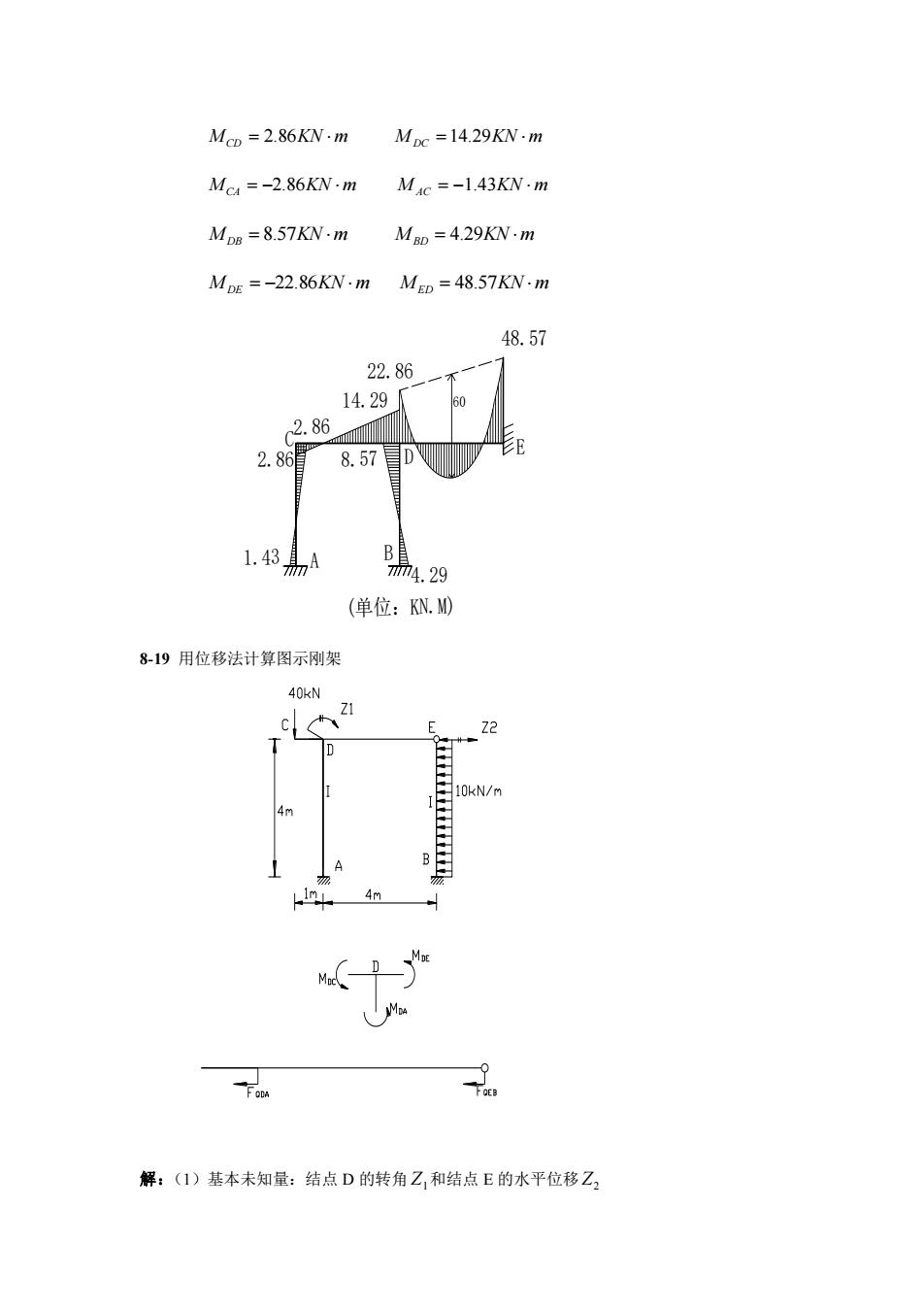
MCD = 2.86KN m MDC =14.29KN m MCA = −2.86KN m M AC = −1.43KN m MDB = 8.57KN m MBD = 4.29KN m MDE = −22.86KN m MED = 48.57KN m 2.86 1.43 2.86 4.29 14.29 22.86 8.57 48.57 A C B D E (单位:KN.M) 60 8-19 用位移法计算图示刚架 解:(1)基本未知量:结点 D 的转角 Z1 和结点 E 的水平位移 Z2

(2)写出杆端弯矩表达式 Moc=40KN.m 42 Mu=3x2乙 M-2g2-62 Mu=-3×是石+g10x4 (3)列平衡方程 Moc Mp+Mos =0 20EIZ,-3E1Z2+320=0 FoD4+FoER=0 -+040 4 4 解得:乙=-3368 乙=-11787 EI E (4)杆端弯矩 Mo4=10.52KN.m M4D=27.36KN.m ME=-50.52KNm MBE =-42.10KN.m 5052 ☐27.36 M (kN/m) 8-20试证明图示结构结点C的转角等于零
(2)写出杆端弯矩表达式 M DC = 40KN m 1 2 2 4 6 4 4 Z EI Z EI M DA = − 1 4 2 3 Z EI M DE = 1 2 2 4 6 4 2 Z EI Z EI M AD = − 2 2 2 10 4 8 1 4 = −3 Z + EI M BE (3)列平衡方程 MDC + M DA + MDE = 0 20EIZ1 −3EIZ2 + 320 = 0 FQDA + FQEB = 0 10 4 0 2 1 4 4 2 − + = + − MDA M AD MBE 解得: EI Z 33.68 1 = − EI Z 117.87 2 − = (4)杆端弯矩 MDA =10.52KN m MAD = 27.36KN m MDE = −50.52KN m MBE = −42.10KN m 8-20 试证明图示结构结点 C 的转角等于零

解法一: 基本未知量:结点C的转角Z,和结点D的铅垂位乙, 1. 基本体 6i/ m 5,=1i 31=0 2=0 Rip=0 Rap=Fp
解法一: 基本未知量:结点 C 的转角 Z1 和结点 D 的铅垂位 Z2 r 11i 11 = r21 = 0 r12 = 0 22 2 27 l i r = − R1P = 0 R2P = FP

11Z,=0 Z=0 -平2+5=0 石品 解法二:直接平衡法 (1)基本未知量:结点C的转角Z,和结点D的铅垂位移Z (2)写出杆端弯矩表达式 Mc-2z-2- =好-鸟名+号 2鸟号 以e=2z+2+号 McD=3iZ Mon (3)列平衡方程 Mc Mce Mc =0 11iZ,=0 Z,=0 Fca+FDE-FCB=0 2z,+2z,-F1=0 8-28试利用对称性将图示刚架取相应的半结构,采用适宜的方法进行计算。 ,W. 一美 4D 1 阳-8 半结构圈 i血 解:取半边结构进行计算
0 27 11 0 2 2 1 − + = = Z FP l i iZ i F l Z Z P 27 0 2 2 1 = = 解法二:直接平衡法 (1)基本未知量:结点 C 的转角 Z1 和结点 D 的铅垂位移 Z2 (2)写出杆端弯矩表达式 8 6 2 1 2 F l Z l i M iZ P AC = − − 8 6 4 1 2 F l Z l i M iZ P CA = − + 8 6 4 1 2 F l Z l i M iZ P CB = + − 8 6 2 1 2 F l Z l i M iZ P BC = + + 3 1 MCD = iZ 2 3 Z l i M ED = − (3)列平衡方程 MCA + MCB + MCD = 0 11iZ1 = 0 Z1 = 0 FCA + FDE − FCB = 0 0 27 2 1 + Z2 − F l = l i iZ P i F l Z P 27 2 2 = 8-28 试利用对称性将图示刚架取相应的半结构,采用适宜的方法进行计算。 解:取半边结构进行计算
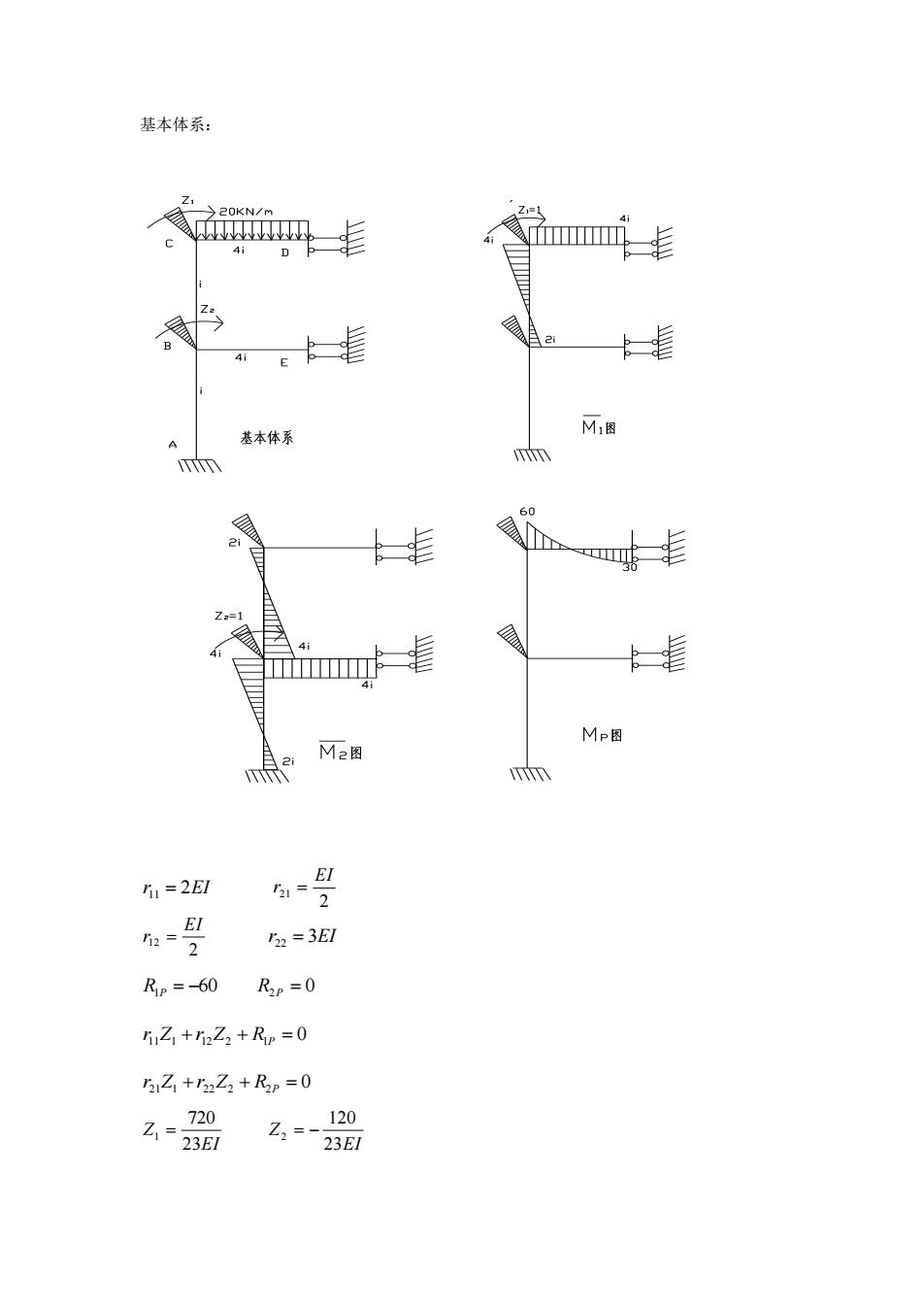
基本体系: mi叶毛 ”卡人指 基本体系 M西 A n 4i F MP图 M2图 h1=2E1 号 52=3El Rp=-60Rp=0 5,Z+r2Z2+Rp=0 51Z+5Z3+Rp=0 -瑞名删
基本体系: r 2EI 11 = 2 21 EI r = 2 12 EI r = r 3EI 22 = R1P = −60 R2P = 0 r11Z1 + r12Z2 + R1P = 0 r21Z1 + r22Z2 + R2P = 0 EI Z 23 720 1 = EI Z 23 120 2 = −

287 8.7 28. M图 (kN.m)
(kN.m)