
第2章几何机动分析 2-1几何不变体系与几何可变体系 2-2几何不变体系的组成规律 2-3瞬变体系与常变体系 2-4例题与习题
第2章 几何机动分析 2-1几何不变体系与几何可变体系 2-2几何不变体系的组成规律 2-3瞬变体系与常变体系 2-4例题与习题
2-1几何不变体系与几何可变体系 不考虑材料的变形 在任意荷载作用下,体系的几何 形状和位置都不会改变。 在任意荷载作用下,无论荷载多么 小,体系的几何形状都有可能改变。 在任意荷载作用下,无论荷载多么 小,体系的位置都有可能改变
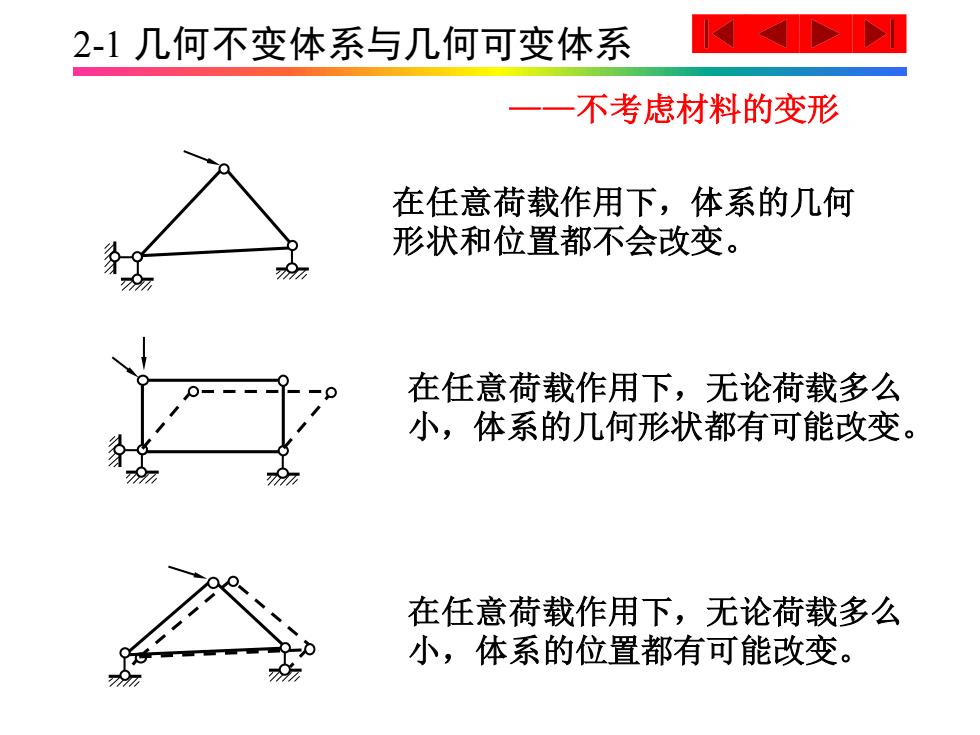
2-1 几何不变体系与几何可变体系 ——不考虑材料的变形 在任意荷载作用下,体系的几何 形状和位置都不会改变。 在任意荷载作用下,无论荷载多么 小,体系的几何形状都有可能改变。 在任意荷载作用下,无论荷载多么 小,体系的位置都有可能改变
2-1几何不变体系与几何可变体系 几何不变体系:不考虑材料的弹性变形,结构在任意荷载 作用下,其几何形状和位置都不能改变。 几何可变体系:不考虑材料的弹性变形,尽管结构受到很小 的作用力,其几何形状或位置都可能改变。 刚片:可以看成是几何不变体系(刚体)的物体。 (可以是杆、由杆组成的结构、支撑结构的地基) 刚片Ⅱ 刚片I 87777777 刚片Ⅲ
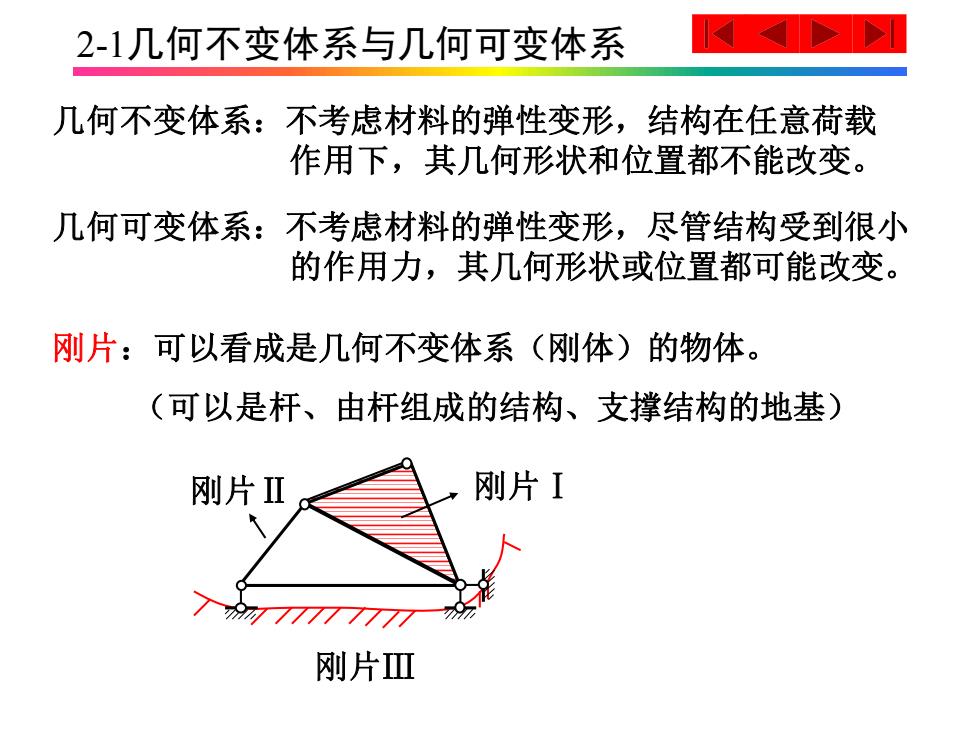
2-1几何不变体系与几何可变体系 刚片Ⅰ 几何可变体系:不考虑材料的弹性变形,尽管结构受到很小 的作用力,其几何形状或位置都可能改变。 刚片:可以看成是几何不变体系(刚体)的物体。 (可以是杆、由杆组成的结构、支撑结构的地基) 几何不变体系:不考虑材料的弹性变形,结构在任意荷载 作用下,其几何形状和位置都不能改变。 刚片Ⅱ 刚片Ⅲ
2-1几何不变体系与几何可变体系 自由度:确定体系位置所需的独立坐标数 约束:一种减少自由度的装置 自由度:2 自由度:1 自由度:0
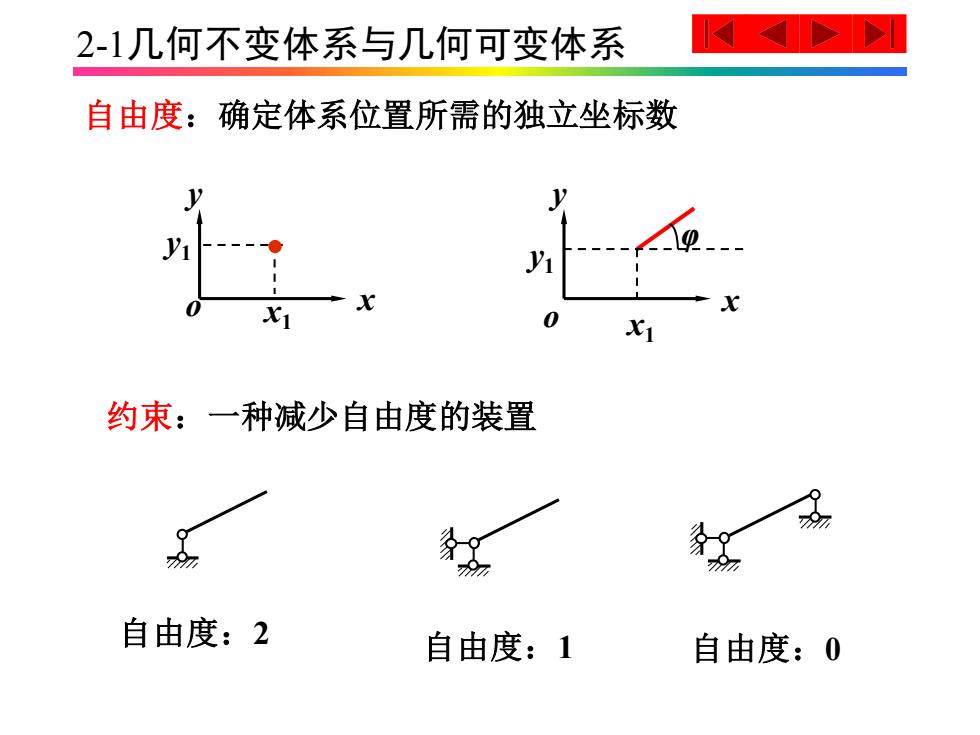
2-1几何不变体系与几何可变体系 x1 y1 自由度:确定体系位置所需的独立坐标数 约束:一种减少自由度的装置 x y o x y o x1 y1 φ 自由度:2 自由度:1 自由度:0
2-1几何不变体系与几何可变体系 常见约束 1链杆:两端用铰与其它物体相连的刚片, 可以是直杆、折杆、曲杆: 作用:一个支链杆可以减 少一个自由度。 2单铰:连接两个刚片的铰; 作用:一个单铰可以减 少二个自由度。 两个不共线的支链杆相当于一个单铰
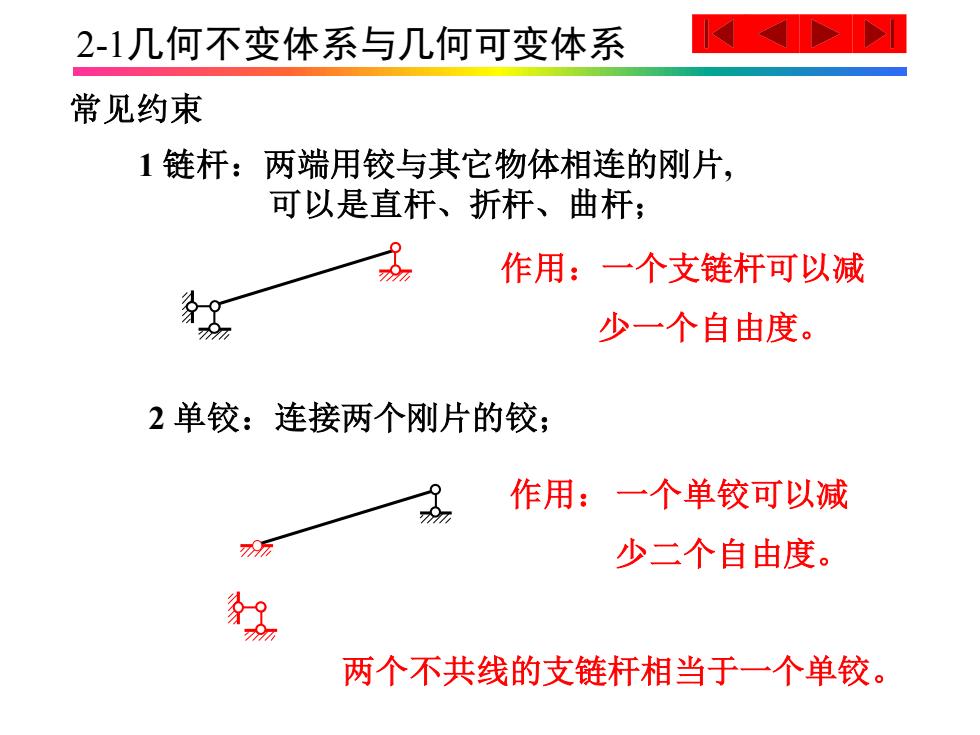
2-1几何不变体系与几何可变体系 常见约束 1 链杆:两端用铰与其它物体相连的刚片, 可以是直杆、折杆、曲杆; 作用:一个支链杆可以减 少一个自由度。 2 单铰:连接两个刚片的铰; 作用: 一个单铰可以减 少二个自由度。 两个不共线的支链杆相当于一个单铰
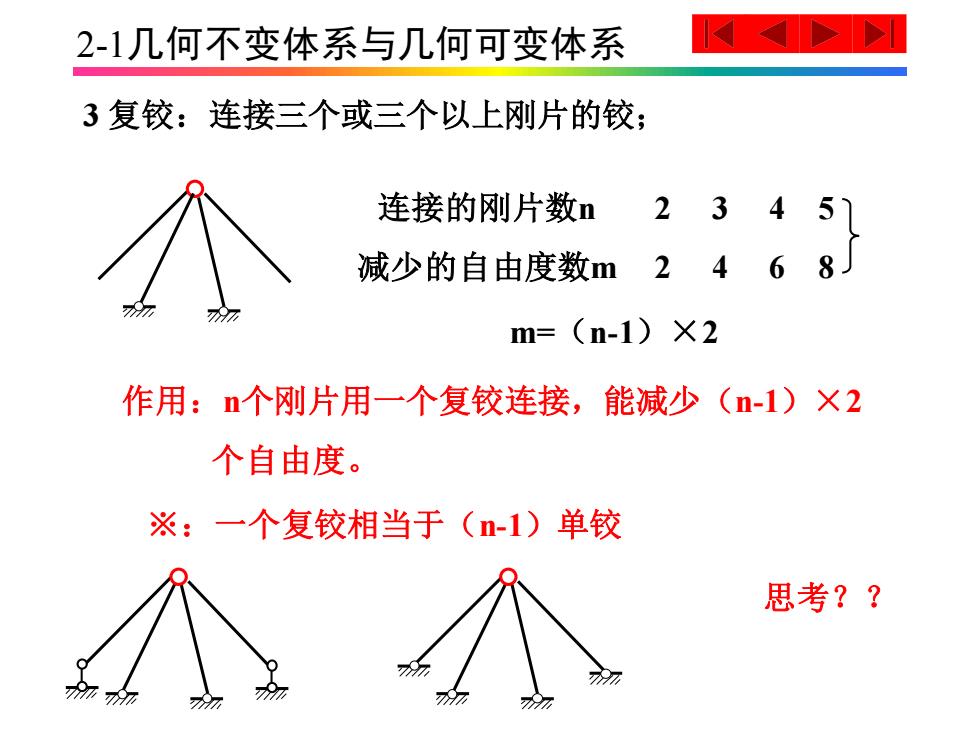
2-1几何不变体系与几何可变体系 3复铰:连接三个或三个以上刚片的铰; 连接的刚片数n 2345 减少的自由度数m2468」 m=(n-1)×2 作用:n个刚片用一个复铰连接,能减少(n-1)×2 个自由度。 ※:一个复铰相当于(n-1)单铰 思考??
2-1几何不变体系与几何可变体系 3 复铰:连接三个或三个以上刚片的铰; 作用:n个刚片用一个复铰连接,能减少(n-1)×2 个自由度。 连接的刚片数n 减少的自由度数m 2 2 3 4 4 6 5 8 m=(n-1)×2 ※:一个复铰相当于(n-1)单铰 思考??

2-1几何不变体系与几何可变体系 4固定端:可以减少三个自由度。 5平行支链杆:可以减少二个自由度。 度
2-1几何不变体系与几何可变体系 4 固定端:可以减少三个自由度。 5 平行支链杆:可以减少二个自由度
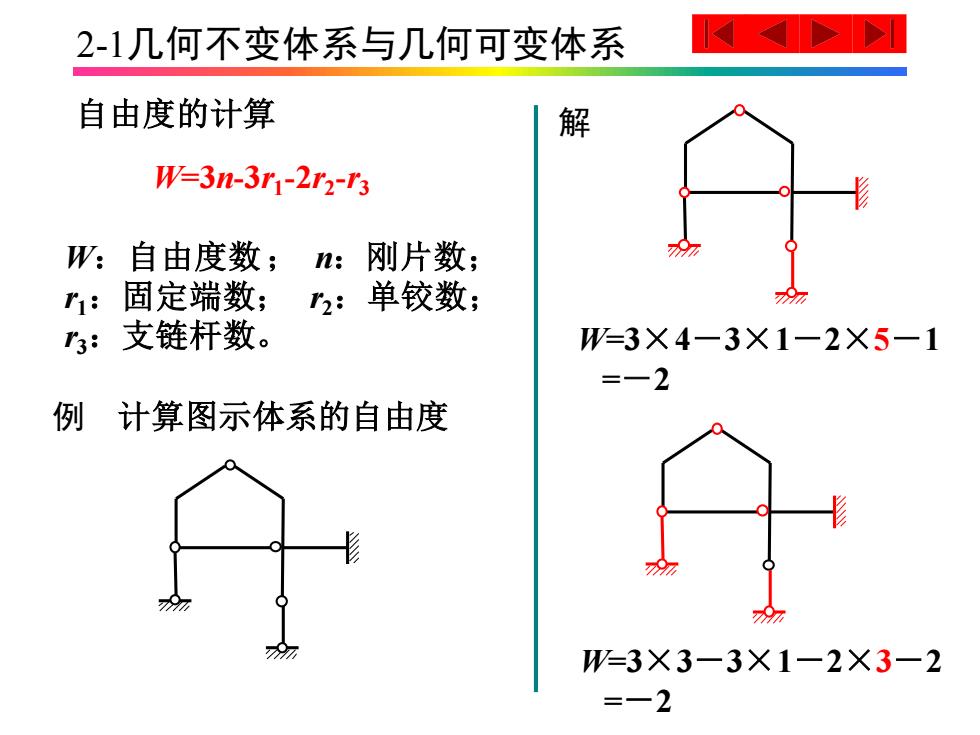
2-1几何不变体系与几何可变体系 自由度的计算 解 W=3n-3r1-2r2-3 W:自由度数; n: 刚片数; r:固定端数; 2:单铰数; 3: 支链杆数。 W=3×4一3×1一2×5一1 =一2 例计算图示体系的自由度 9 97 9 W=3X3一3X1一2X3-2 =一2
2-1几何不变体系与几何可变体系 自由度的计算 W:自由度数; n:刚片数; r1:固定端数; r2:单铰数; r3:支链杆数。 W=3×4-3×1-2×5-1 =-2 W=3×3-3×1-2×3-2 =-2 例 计算图示体系的自由度 W=3n-3r1 -2r2 -r3 解
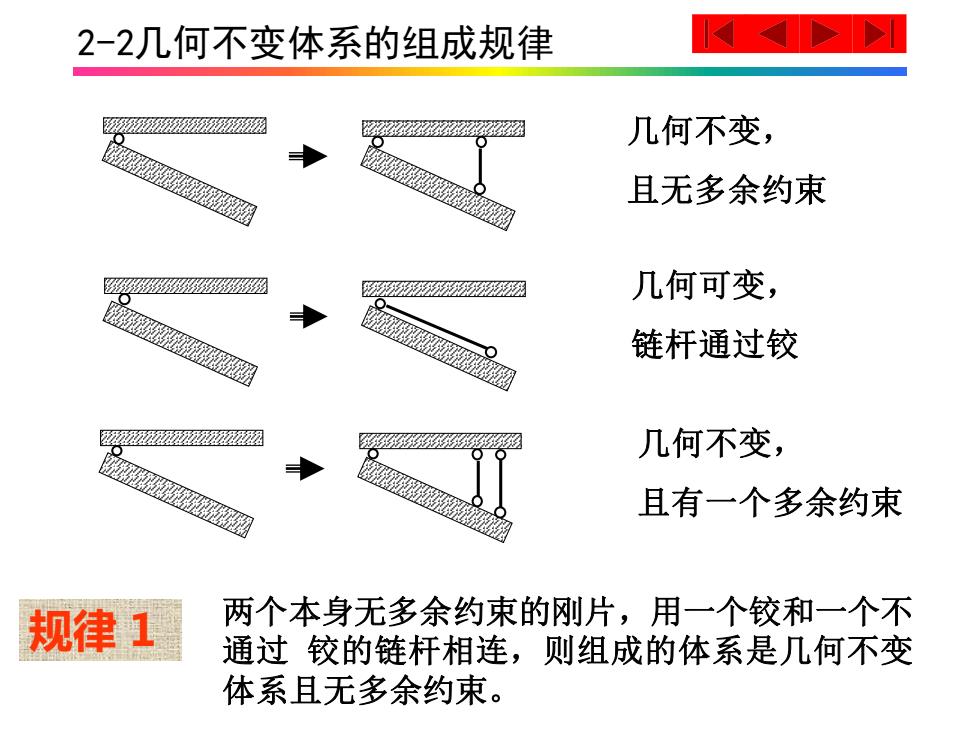
2-2几何不变体系的组成规律 几何不变, 且无多余约束 A 麻 几何可变, 链杆通过铰 ☑ 几何不变, 且有一个多余约束 规律1 两个本身无多余约束的刚片,用一个铰和一个不 通过铰的链杆相连,则组成的体系是几何不变 体系且无多余约束
2-2几何不变体系的组成规律 几何不变, 且无多余约束 几何可变, 链杆通过铰 几何不变, 且有一个多余约束 两个本身无多余约束的刚片,用一个铰和一个不 通过 铰的链杆相连,则组成的体系是几何不变 体系且无多余约束。 规律 1
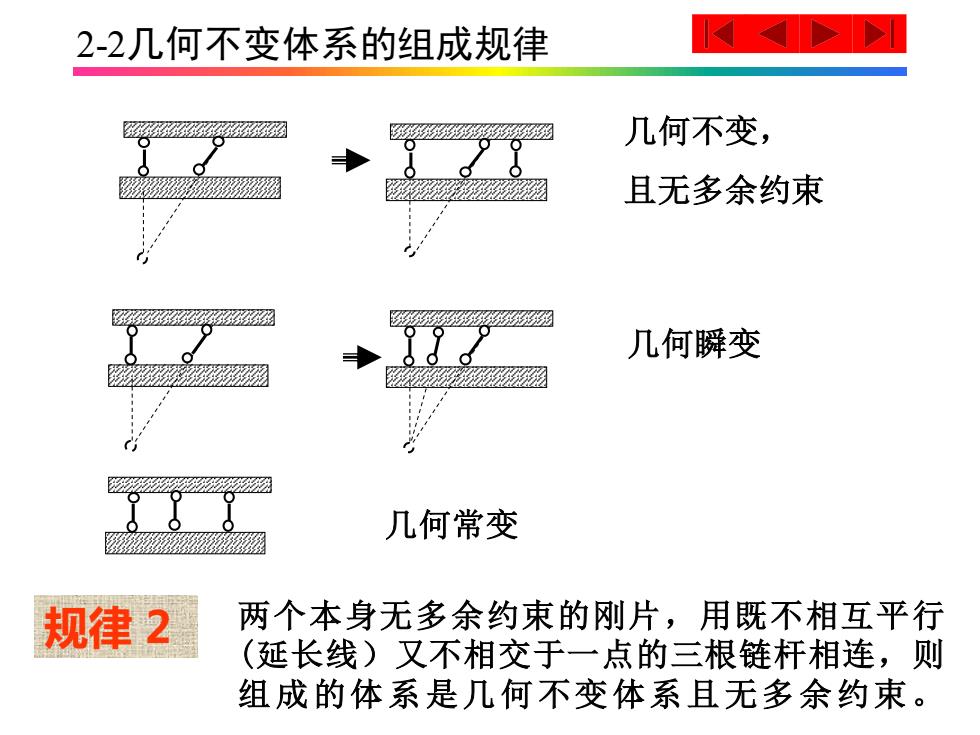
2-2几何不变体系的组成规律 形 几何不变, 且无多余约束 几何瞬变 几何常变 规律2 两个本身无多余约束的刚片,用既不相互平行 (延长线)又不相交于一点的三根链杆相连,则 组成的体系是几何不变体系且无多余约束
2-2几何不变体系的组成规律 几何不变, 且无多余约束 几何瞬变 两个本身无多余约束的刚片,用既不相互平行 (延长线)又不相交于一点的三根链杆相连,则 组成的体系是几何不变体系且无多余约束。 规律 2 几何常变