
浅议结构力学教学中培养学生勾画变形图能力的重要作用 式汉理工大学谢官模 在结构力学的教学中,勾画结构在荷载作用下的变形图是一个难点,在教学 大纲和教材中也没提出具体要求。我在结构力学教学实践中,在保证大纲要求的 基本教学内容的前提下,有意识地培养学生勾画梁、刚架类弯曲变形结构的变形 图的能力,对于学生快速画弯矩图及检查所画的弯矩图、确定位移法中固端弯矩 的符号、在结构动力学中判断动力自由度数目及建立运动方程都有很大的帮助。 在图1所示的坐标系中,对于小变形的情况,杆件的挠曲线微分方程为 M(x)=Ely"(x) 杆件下侧受拉时,弯矩为正,挠 曲线二阶导数为正,挠曲线向下 凸;反之,杆件上侧受拉时,弯 矩为负,挠曲线二阶导数为负, 图1杆件的挠曲线 挠曲线向上凸。因此,对于直杆的弯曲变形,挠曲线的凸向与杆件的受拉侧一致, 杆件哪一侧受拉,挠曲线就向那一侧凸。 对于荷载作用下的梁和刚架类弯曲变形结构,首先根据支座处约束情况勾画 出杆端的变形:然后根据细长杆件不计轴向变形的假设,确定并画出杆与杆相连 接的结点的位移,以及此结点处各杆端的变形:再根据杆上荷载作用情况确定各 反弯点的位置(当然有可能整个杆的挠曲线都向同一侧凸出,没有反弯点),从 而根据支座处杆端变形、反弯点、结点处杆端变形情况,或两个结点处杆端变形 反弯点情况,画出整个杆的变形,进而画出整个结构的变形。 勾画梁和刚架类结构的变形图,再利用弯矩、剪力与荷载集度的微分关系, 有助于快速画出结构在荷载作用下的弯矩图轮廓,或者对所求出的弯矩图进行检 查,看是否有明显的错误。如图2()所示的刚架横梁受均布荷载作用,A为固定 (c) 图2刚架的变形图与弯矩图的对应关系
浅议结构力学教学中培养学生勾画变形图能力的重要作用 武汉理工大学 谢官模 在结构力学的教学中,勾画结构在荷载作用下的变形图是一个难点,在教学 大纲和教材中也没提出具体要求。我在结构力学教学实践中,在保证大纲要求的 基本教学内容的前提下,有意识地培养学生勾画梁、刚架类弯曲变形结构的变形 图的能力,对于学生快速画弯矩图及检查所画的弯矩图、确定位移法中固端弯矩 的符号、在结构动力学中判断动力自由度数目及建立运动方程都有很大的帮助。 在图 1 所示的坐标系中,对于小变形的情况,杆件的挠曲线微分方程为 M (x) = EIy′′(x) y O x O y x 杆件下侧受拉时,弯矩为正,挠 曲线二阶导数为正,挠曲线向下 凸;反之,杆件上侧受拉时,弯 矩为负,挠曲线二阶导数为负, 图 1 杆件的挠曲线 挠曲线向上凸。因此,对于直杆的弯曲变形,挠曲线的凸向与杆件的受拉侧一致, 杆件哪一侧受拉,挠曲线就向那一侧凸。 对于荷载作用下的梁和刚架类弯曲变形结构,首先根据支座处约束情况勾画 出杆端的变形;然后根据细长杆件不计轴向变形的假设,确定并画出杆与杆相连 接的结点的位移,以及此结点处各杆端的变形;再根据杆上荷载作用情况确定各 反弯点的位置(当然有可能整个杆的挠曲线都向同一侧凸出,没有反弯点),从 而根据支座处杆端变形、反弯点、结点处杆端变形情况,或两个结点处杆端变形、 反弯点情况,画出整个杆的变形,进而画出整个结构的变形。 勾画梁和刚架类结构的变形图,再利用弯矩、剪力与荷载集度的微分关系, 有助于快速画出结构在荷载作用下的弯矩图轮廓,或者对所求出的弯矩图进行检 查,看是否有明显的错误。如图 2(a)所示的刚架横梁受均布荷载作用,A 为固定 B C EI EI A q q D . . E 反弯点 反弯点 (a) (b) (c) 图 2 刚架的变形图与弯矩图的对应关系

端,C端为铰支座。AB杆段无荷载作用,弯矩图为斜直线,BC杆上受竖直向下 的均布荷载作用,弯矩图为向下凸的二次抛物线。由于不计杆件的轴向变形,结 点B没有线位移,只有角位移。根据结构的荷载及刚结点B的特点,可以判断 AB杆和BC杆各有一反弯点D,E,如图2(b)所示,从而画出图示的变形图。在反 弯点D上方,挠曲线向左凸,杆件一定是左侧受拉,而在反弯点D下方,挠曲 线向右凸,杆件一定是右侧受拉,因此可画出AB杆的弯矩图轮廓如图2(©)所示。 同理,在反弯点E左边,挠曲线向上凸,杆件一定是上侧受拉,而在反弯点E 右边,挠曲线向下凸,杆件一定是下侧受拉,据此也可画出图中所示的BC杆的 弯矩图轮廓。变形图上的反弯点对应于弯矩图上弯矩为零的点。 勾画超静定梁在荷载作用下的弯矩图,有助于快速确定位移法中杆件的固端 弯矩的符号。学生用位移法求解静定或超静定结构时,弯矩符号的确定是一个难 点。固端弯矩是单独考虑由荷载引起的杆端弯矩,也就是让杆件的结点位移(注 意只是位移法基本未知量的位移)为零、支座保留原状得到的超静定杆在荷载作 用下的杆端弯矩。我津议学生只记几种典型留静定梁(即两端固定、一端固定 “端铰支座或链杆支座、一端固定一端滑动支座的情况)在集中力或均布荷载作 用下杆端弯矩的绝对值。在确定固端弯矩的计算简图后,首先根据记忆写出固端 弯矩的绝对值,其符号则根据变形图来确定。因为教材中虽有固端弯矩表可查 但只给出了水平方位杆件的若干支座组合情况下的固端弯矩,对于一般方位、任 意支座组合的杆件的固端弯矩,通过勾画变形图来确定固端弯矩的符号将很方 便。根据杆端挠曲线的凸向确定哪侧受拉,据此画出顺时针或逆时针的箭头,顺 时针的固端弯矩为正,逆时针的固端弯矩为负。如图3所示的情况,梁AB长为 L,在其中点受水平向左的集中力P作用 则有M=3PL/8,M=PL/8,勾画出 M 梁的变形如图中所示,在反弯点C的上方 挠曲线向左凸,杆一定是左侧受拉(包括 杆的上端),根据上端B的左侧受拉画出 顺时针的箭头,因此上端的固端弯矩为正: 在反弯点C的下方,挠曲线向右凸,杆一 定是右侧受拉(包括杆的下端),根据杆 下端A的右侧受拉画出顺时针的箭头,故 M 梁下端的固端弯矩也为正。 图3由变形图确定固端弯矩符号 在结构力学的学习中培养学生勾画梁、刚架类弯曲变形结构的变形图,也有 助于在结构动力学中正确判断结构动力自由度的数目,以及建立结构振动的运动 微分方程。结构动力自由度数就是确定结构的全部质量在任何时刻所处位置所需
端,C 端为铰支座。AB 杆段无荷载作用,弯矩图为斜直线,BC 杆上受竖直向下 的均布荷载作用,弯矩图为向下凸的二次抛物线。由于不计杆件的轴向变形,结 点 B 没有线位移,只有角位移。根据结构的荷载及刚结点 B 的特点,可以判断 AB 杆和 BC 杆各有一反弯点 D,E,如图 2(b)所示,从而画出图示的变形图。在反 弯点 D 上方,挠曲线向左凸,杆件一定是左侧受拉,而在反弯点 D 下方,挠曲 线向右凸,杆件一定是右侧受拉,因此可画出 AB 杆的弯矩图轮廓如图 2(c)所示。 同理,在反弯点 E 左边,挠曲线向上凸,杆件一定是上侧受拉,而在反弯点 E 右边,挠曲线向下凸,杆件一定是下侧受拉,据此也可画出图中所示的 BC 杆的 弯矩图轮廓。变形图上的反弯点对应于弯矩图上弯矩为零的点。 勾画超静定梁在荷载作用下的弯矩图,有助于快速确定位移法中杆件的固端 弯矩的符号。学生用位移法求解静定或超静定结构时,弯矩符号的确定是一个难 点。固端弯矩是单独考虑由荷载引起的杆端弯矩,也就是让杆件的结点位移(注 意只是位移法基本未知量的位移)为零、支座保留原状得到的超静定杆在荷载作 用下的杆端弯矩。我建议学生只记忆几种典型超静定梁(即两端固定、一端固定 一端铰支座或链杆支座、一端固定一端滑动支座的情况)在集中力或均布荷载作 用下杆端弯矩的绝对值。在确定固端弯矩的计算简图后,首先根据记忆写出固端 弯矩的绝对值,其符号则根据变形图来确定。因为教材中虽有固端弯矩表可查, 但只给出了水平方位杆件的若干支座组合情况下的固端弯矩,对于一般方位、任 意支座组合的杆件的固端弯矩,通过勾画变形图来确定固端弯矩的符号将很方 便。根据杆端挠曲线的凸向确定哪侧受拉,据此画出顺时针或逆时针的箭头,顺 时针的固端弯矩为正,逆时针的固端弯矩为负。如图 3 所示的情况,梁 AB 长为 L,在其中点受水平向左的集中力 P 作用。 AB F F M BA A B P . 反弯点C M 则有 M 3PL / 8, M PL / 8 F BA F AB = = ,勾画出 梁的变形如图中所示,在反弯点 C 的上方, 挠曲线向左凸,杆一定是左侧受拉(包括 杆的上端),根据上端 B 的左侧受拉画出 顺时针的箭头,因此上端的固端弯矩为正; 在反弯点 C 的下方,挠曲线向右凸,杆一 定是右侧受拉(包括杆的下端),根据杆 下端 A 的右侧受拉画出顺时针的箭头,故 梁下端的固端弯矩也为正。 图 3 由变形图确定固端弯矩符号 在结构力学的学习中培养学生勾画梁、刚架类弯曲变形结构的变形图,也有 助于在结构动力学中正确判断结构动力自由度的数目,以及建立结构振动的运动 微分方程。结构动力自由度数就是确定结构的全部质量在任何时刻所处位置所需
的独立的几何参数数目,正确判断动力自由度数目是建立振动微分方程的基础。 在勾画出结构的变形图之后,根据质量所在处结构的变形情况,即可选择一组独 立的几何参数来描述结构所有质量的运动,这些几何参数的数目就是结构的动力 自由度数目。如图4所示的刚架结构有4个集中质量,画出结构在某一时刻的变 形图,可确定此动力系统的自由度数为2,用两个横梁的侧移x(t),x2(t)即可确 定4个集中质量在任何时刻的位置。再如图5所示的结构动力系统,勾画出结构 x(t) 图4根据变形图确定动力自由度 图5根据变形图建立振动方程 的变形图,可知此系统为单自由度系统,并可用柔度法写出质量振动的微分方程 x(t)=d,·(-mi)+62·Psint 其中柔度系数6,6,的物理意义也可由此变形图来描述
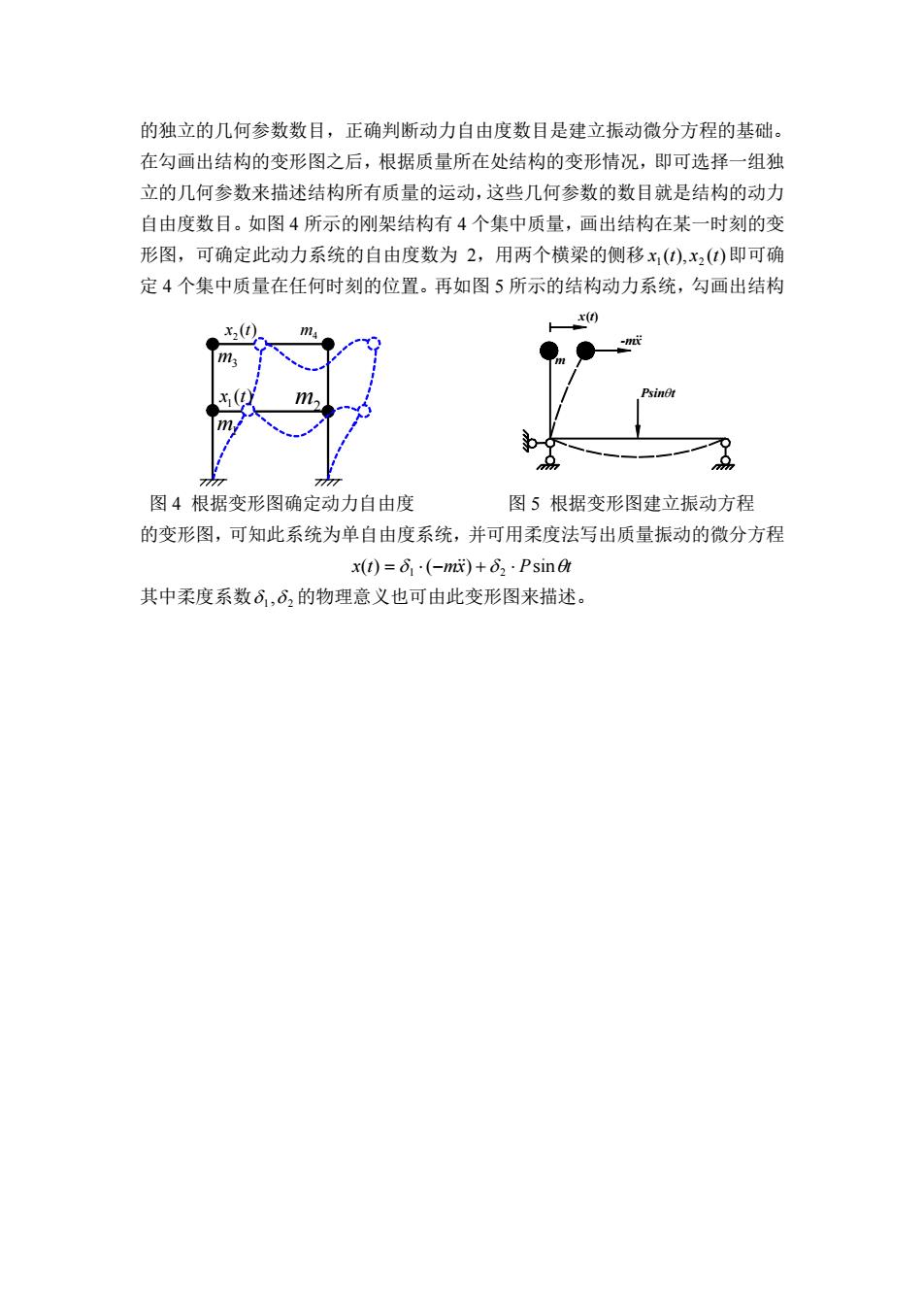
的独立的几何参数数目,正确判断动力自由度数目是建立振动微分方程的基础。 在勾画出结构的变形图之后,根据质量所在处结构的变形情况,即可选择一组独 立的几何参数来描述结构所有质量的运动,这些几何参数的数目就是结构的动力 自由度数目。如图 4 所示的刚架结构有 4 个集中质量,画出结构在某一时刻的变 形图,可确定此动力系统的自由度数为 2,用两个横梁的侧移 即可确 定 4 个集中质量在任何时刻的位置。再如图 5 所示的结构动力系统,勾画出结构 ( ), ( ) 1 2 x t x t m Psin t θ x(t) -mx . m1 m2 m3 m4 ( ) 1 x t ( ) 2 x t 图 4 根据变形图确定动力自由度 图 5 根据变形图建立振动方程 的变形图,可知此系统为单自由度系统,并可用柔度法写出质量振动的微分方程 x(t) δ ( mx) δ Psinθt 1 2 = ⋅ − && + ⋅ 其中柔度系数 1 2 δ ,δ 的物理意义也可由此变形图来描述