
第八章位移法 §8-1位移法的基本思路 超静定结构两类解法: 力法:思路及步骤,适用于所有静定结构计算。有时太繁。 从别的角度考虑:内力和位移之间的关系随外因的确定而确定。 先求位移在求内力→位移法,适用于超静定梁和刚架。 我们知道,当结构所受外因(外荷载、支座位移、温度变化等)一定一内力一定一 变形一定→位移一定,也就是结构的内力和位移之间有确定的关系(这也可以从位移的 公式反映出来)。 力法:先求内力一再求位移,以多余力为基本未知量,能否反过来,也就是先求 位移一再求内力,即以结构的某些位移为基本未知量,先想办法求出这些位移,再求出 内力。这就出现了位移法。 目前通用的位移法有两种:英国的、俄罗斯的,两者的实质是相同的。 以结构的某些结点位移作为基本未知量,由静力平衡条件先求出他们,再据以求出 结构的内力和其它位移。 这种方法可以用于求解一些超静定梁和刚架,十分方便。 例:上面的例子,用位移法求解,只有结点转角一个未知量。 下面,我们通过一个简单的例子来说明位移法的解题思路和步骤: 一个两跨连续梁,一次超静定,等截面EI=常数,右跨作用有均布荷载q,(当然可 以用力法求解),在荷载q作用下,结构会发生变形,无N,无轴向变形,B点无竖向 位移,只有转角pB。且B点是一个刚结点传递M:变形时各杆端不能发生相对转动和 移动,刚结点所连接的杆件之间角度受力以后不变。也就是AB、BC杆在结点B处的 转角是相同的。原结构的受力和变形情况和b是等价的。 B当作固定端又产生转角pB。 以 R a(原结构) AB: 人 BC: 如果把转角当作支座位移这一外因看,则原结构的计算就可以变成两个单跨超静 定梁来计算
1 第八章 位移法 §8-1 位移法的基本思路 超静定结构两类解法: 力法:思路及步骤,适用于所有静定结构计算。有时太繁, 从别的角度考虑:内力和位移之间的关系随外因的确定而确定。 先求位移在求内力→ 位移法,适用于超静定梁和刚架。 我们知道,当结构所受外因(外荷载、支座位移、温度变化等)一定内力一定 变形一定位移一定,也就是结构的内力和位移之间有确定的关系(这也可以从位移的 公式反映出来)。 力法:先求内力再求位移,以多余力为基本未知量.,能否反过来,也就是先求 位移再求内力,即以结构的某些位移为基本未知量,先想办法求出这些位移,再求出 内力。这就出现了位移法。 目前通用的位移法有两种:英国的、俄罗斯的,两者的实质是相同的。 以结构的某些结点位移作为基本未知量,由静力平衡条件先求出他们,再据以求出 结构的内力和其它位移。 这种方法可以用于求解一些超静定梁和刚架,十分方便。 例:上面的例子,用位移法求解,只有结点转角一个未知量。 下面,我们通过一个简单的例子来说明位移法的解题思路和步骤: 一个两跨连续梁,一次超静定,等截面 EI=常数,右跨作用有均布荷载 q,(当然可 以用力法求解),在荷载 q 作用下,结构会发生变形,无 N,无轴向变形,B 点无竖向 位移,只有转角B。且 B 点是一个刚结点传递 M;变形时各杆端不能发生相对转动和 移动,刚结点所连接的杆件之间角度受力以后不变。也就是 AB、BC 杆在结点 B 处的 转角是相同的。原结构的受力和变形情况和 b 是等价的。 B 当作固定端又产生转角B。 a(原结构) AB: BC: b 如果把转角B当作支座位移这一外因看,则原结构的计算就可以变成两个单跨超静 定梁来计算

显然,只要知道B,两个单跨静定梁的计算可以用力法求解出全部反力和内力,现 在的未知量是pB(位移法的基本未知量)。 关键:如何求oB?求出pB后又如何求梁的内力?又如何把a=b来计算? 我们采用了这样的方法: 假定在刚结点B附加一刚臂(T),限制B点转角,B一固定端(无线位移,无转 动)(略轴向变形)原结构就变成了AB、BC两个单跨超静定梁的组合体: AB: ,BC: 但现在和原结构的变形不符,⑨,所以为保持和原结构等效,人为使B结点发生与 实际情况相同的转角φB(以Z表示,统一)。一紧一松,两者抵消,C结构和原结构等 效,也就是:两者受力和变形相同。C称原结构的基本结构,a、b、c三个结构是相同 的,现在我们可以用基本结构来代替原结构的计算,C的未知量是乙,求Z的条件是 什么呢? 附加刚臂本身没有,加上去限制转动后又放松,所以要等效,刚臂不应受力。(不 产生反力)。也就是基本结构在原荷载q和Z1(B)的共同作用下使附加刚臂上的反力 偶等于0。取出B点作为隔离体R=O,要求R1用叠加法。 1)基本结构在原结构荷载q单独作用下,用力法求出BC的M图,AB段=0,取出B 作为隔离体,平衡,刚臂上反力偶R1=一qP8(和Z1同向为+),基本结构在原荷载单 独作用下在附加刚臂上产生的反力偶。 玛 B n 2)在Z1单独作用下力法求出(M2图),B隔离体。 R=6日乙一基本结构在乙单独作用下“、”上的反力偶。 共同作用下,叠加:R,+R=R=0,6但乙,+仁g)=0,带Z算不方便,也不 通用,在Z1处加单位转角乙→f、M,图 =6,R=r1Z队成比例) Z+Rp=0 位移法的典型方程,其中当1、RP和Z同向为正。 求出Z1= S后,最后M图叠加,M=M,+乙·M,即原结构的M图,由杆
2 显然,只要知道B,两个单跨静定梁的计算可以用力法求解出全部反力和内力,现 在的未知量是B(位移法的基本未知量)。 关键:如何求B?求出B 后又如何求梁的内力?又如何把 ab 来计算? 我们采用了这样的方法: 假定在刚结点 B 附加一刚臂(▼),限制 B 点转角,B固定端(无线位移,无转 动)(略轴向变形)原结构就变成了 AB、BC 两个单跨超静定梁的组合体: AB: ,BC: 但现在和原结构的变形不符,B,所以为保持和原结构等效,人为使 B 结点发生与 实际情况相同的转角B(以 Z1 表示,统一)。一紧一松,两者抵消,C 结构和原结构等 效,也就是:两者受力和变形相同。C 称原结构的基本结构,a、b、c 三个结构是相同 的,现在我们可以用基本结构来代替原结构的计算,C 的未知量是 Z1,求 Z1 的条件是 什么呢? 附加刚臂本身没有,加上去限制转动后又放松,所以要等效,刚臂不应受力。(不 产生反力)。也就是基本结构在原荷载 q 和 Z1(B)的共同作用下使附加刚臂上的反力 偶等于 0。取出 B 点作为隔离体 R1=0,要求 R1 用叠加法。 1)基本结构在原结构荷载 q 单独作用下,用力法求出 BC 的 M 图,AB 段=0,取出 B 作为隔离体,平衡,刚臂上反力偶 R1P= —ql2 /8(和 Z1 同向为+),基本结构在原荷载单 独作用下在附加刚臂上产生的反力偶。 A q B C 2)在 Z1 单独作用下力法求出( M Z1 图),B 隔离体。 11 1 6 Z l EI R = ——基本结构在 Z1 单独作用下“▼”上的反力偶。 共同作用下,叠加: R11 + R1P = R1 = 0, ) 0 8 1 ( 6 2 Z1 + − ql = l EI ,带 Z1 算不方便,也不 通用,在 Z1 处加单位转角 Z1 f、M1 图 0 6 11 1 1 11 1 11 1 + = = = Z R P r R r Z l EI r , (成比例) 位移法的典型方程,其中当 r11、R1P 和 Z1同向为正。 求出 EI ql Z 48 3 1 = 后,最后 M 图叠加, M M P Z1 M1 = + • ,即原结构的 M 图,由杆

件平衡作出Q图。 简单地重复一下思路: 比较力法和位移法可知:(异同点 两者所选取的基本未知量不同: 力法:基本未知量为多余的未知力 位移法:基本未知量为结点位移 思路不同,途径不同: 但所遵循的原则是一致的:利用基本结构和原结构的受力和变形相同的条件求解。 力法的基本结构是静定结构,利用多余力处的位移条件建立力法典型方程,求多余 力,将超静定结构一静定结构来求解 依据:静定结构的内力和位移计算。并且基本结构形式可能会很多。 位移法的基本结构(一般是唯一的):单跨超静定梁的组合体(可以分开计算)。利 用附加联系处的力的平衡条件建立位移法典型方程。求出结点位移未知量。 依据:以力法和单跨超静定梁的计算作为计算基础,单跨超静定梁的形式较少,计 算可先列出通式算出来或制成表格直接查用。这是下一节的内容。 从一例→第一节位移法的基本思路 一、位移法的解题思路 超静定结构求解的前提: 当结构形式一定,所受外因(外荷载、支座位移、温度变化等)一定三内力、反力 定→变形一定一位移一定。也就是在一定的外因下,结构的内力和位移之间有确定的 关系。 由思维的正、逆过程,分出超静定结构的两种解法:力法,内力一位移,以多余力 作出基本未知量:位移法:位移一内力,以结构的某些位移为基本未知量,先想办法求 出这些位移,再求出内力一求解一些超静定梁及刚架十分方便。 原结构(受力P作用下变形如图,1处有一结点转角Z1) (在某些结点上加上一定的附加联系(附加刚臂或附加链杆)把这些结点 ,固定端或较支.如图。 基本结构,代替原结构进行计算。(单跨超静定梁的组合体) (要使基本结构保持和原结构完全等效,也就是受力、变形相同) (再使各附加联系处发生与实际相符的位移,当作外因,称位移法的基本未知量) 由于基本结构和原结构完全等效(力、位移),每个附加联系处产生的约 束反力等于0。 则(结论):基本结构在原荷载及这些结点位移共同作用下在各个附加联系上产生的 总约束力等于0的平衡条件建立位移法典型方程。(计算手段:人头顶砖) 利用叠加法分别求出基本结构在原荷载作用下的约束反力 基本结构在各结点未知量作用下的约束反力,叠加法。求这些约束反力的 3
3 件平衡作出 Q 图。 简单地重复一下思路: 比较力法和位移法可知:(异同点) 两者所选取的基本未知量不同; 力法:基本未知量为多余的未知力 位移法:基本未知量为结点位移 思路不同,途径不同; 但所遵循的原则是一致的:利用基本结构和原结构的受力和变形相同的条件求解。 力法的基本结构是静定结构,利用多余力处的位移条件建立力法典型方程,求多余 力,将超静定结构静定结构来求解 依据:静定结构的内力和位移计算。并且基本结构形式可能会很多。 位移法的基本结构(一般是唯一的):单跨超静定梁的组合体(可以分开计算)。利 用附加联系处的力的平衡条件建立位移法典型方程。求出结点位移未知量。 依据:以力法和单跨超静定梁的计算作为计算基础,单跨超静定梁的形式较少,计 算可先列出通式算出来或制成表格直接查用。这是下一节的内容。 从一例 → 第一节 位移法的基本思路 一、位移法的解题思路 超静定结构求解的前提: 当结构形式一定,所受外因(外荷载、支座位移、温度变化等)一定内力、反力 一定变形一定位移一定。也就是在一定的外因下,结构的内力和位移之间有确定的 关系。 由思维的正、逆过程,分出超静定结构的两种解法:力法,内力位移,以多余力 作出基本未知量;位移法:位移内力,以结构的某些位移为基本未知量,先想办法求 出这些位移,再求出内力求解一些超静定梁及刚架十分方便。 原结构(受力 P 作用下变形如图,1 处有一结点转角 Z1) (在某些结点上加上一定的附加联系(附加刚臂或附加链杆)把这些结点 →固定端或铰支,如图。 基本结构,代替原结构进行计算。(单跨超静定梁的组合体) (要使基本结构保持和原结构完全等效,也就是受力、变形相同)。 (再使各附加联系处发生与实际相符的位移,当作外因,称位移法的基本未知量) 由于基本结构和原结构完全等效(力、位移),每个附加联系处产生的约 束反力等于 0。 则(结论):基本结构在原荷载及这些结点位移共同作用下在各个附加联系上产生的 总约束力等于 0 的平衡条件建立位移法典型方程。(计算手段:人头顶砖) 利用叠加法分别求出基本结构在原荷载作用下的约束反力 基本结构在各结点未知量作用下的约束反力,叠加法。求这些约束反力的

基础:单跨超静定梁的转角位移方程 →求解位移法典型方程,求出结点位移未知量 →叠加出最后M(杆件平衡),Q(结点平衡)N作出内力图, 1、弯矩正负问题。 1)正负的规定 2)M成对出现 3)弯矩方向和受拉边的关系 2、附加约束再放松结点位移是解题的一种思路和手段。 3、结合一个简单的刚架例子重述步骤。 位移法基本未知量可以通过作出位移变形图来确定,但比较麻烦,归纳出一般的规 律,和基本结构的选取同时进行。 §8-2等截面直杆的转角位移方程 位移法中将杆件看作单跨超静定梁,杆端位移可看作单跨超静定梁的支座位移。单 跨超静定梁在荷载、支座位移(杆端位移)作用下的杆端弯矩和剪力(杆端内力)之间 的关系式,对于等截面直杆,它们的关系有一个统一的表达式,称为转角位移方程。 本节主要推导此关系式: ·、杆端内力及杆端位移的表示方法及正负号规定: 1、杆端内力(M、Q): Mk、Qk(i杆端,k同一杆的远端):(k为M所属的杆件) 杆端位移(p、△):A:A、VA、PA B:uB、VB、pB △=VB-VA AB两端在垂直于杆轴方向上的相对线位移 B=△n/1 弦转角表杆端的相对线位移 ¥w 2、正负规定: 杆端弯矩MAB、MBA:绕杆端顺时针为正,逆时针为负。(对结点或支座而言,以逆 时针为正) 杆端剪力QAB、QBA:绕隔离体以顺时针转动为+。 结点转角(杆端转角)pA、pB弦转角BB(表杆轴弦转的方向):以顺时针转动为正 两端的相对线位移:以使杆件顺时针转动为正,反之为负。 注:对杆端弯矩作规定,对其它截面弯矩并没作规定。作弯矩图时,应先按此符号规定 正确判定杆件的受拉边,M图画在受拉边,不标正负号。 二、位移法的计算假定: a、忽略轴力产生的轴向变形的影响一①杆件变形前的直线长=变形后的曲线长度
4 基础:单跨超静定梁的转角位移方程 →求解位移法典型方程,求出结点位移未知量 →叠加出最后 M(杆件平衡)→Q(结点平衡)→N 作出内力图。 1、弯矩正负问题。 1)正负的规定 2)M 成对出现 3)弯矩方向和受拉边的关系 2、附加约束再放松结点位移是解题的一种思路和手段。 3、结合一个简单的刚架例子重述步骤。 位移法基本未知量可以通过作出位移变形图来确定,但比较麻烦,归纳出一般的规 律,和基本结构的选取同时进行。 §8-2 等截面直杆的转角位移方程 位移法中将杆件看作单跨超静定梁,杆端位移可看作单跨超静定梁的支座位移。单 跨超静定梁在荷载、支座位移(杆端位移)作用下的杆端弯矩和剪力(杆端内力)之间 的关系式,对于等截面直杆,它们的关系有一个统一的表达式,称为转角位移方程。 本节主要推导此关系式: 一、杆端内力及杆端位移的表示方法及正负号规定: 1、 杆端内力(M、Q): Mik、 Qik (i 杆端,k 同一杆的远端);(ik 为 M 所属的杆件) 杆端位移(、Δ):A:uA、vA、A B:uB、vB、B ΔAB=vB - vA AB 两端在垂直于杆轴方向上的相对线位移 =ΔAB/l 弦转角表杆端的相对线位移 2、正负规定: 杆端弯矩 MAB、MBA:绕杆端顺时针为正,逆时针为负。(对结点或支座而言,以逆 时针为正) 杆端剪力 QAB、QBA:绕隔离体以顺时针转动为+。 结点转角(杆端转角)A、B 弦转角AB(表杆轴弦转的方向):以顺时针转动为正 两端的相对线位移:以使杆件顺时针转动为正,反之为负。 注:对杆端弯矩作规定,对其它截面弯矩并没作规定。作弯矩图时,应先按此符号规定 正确判定杆件的受拉边,M 图画在受拉边,不标正负号。 二、位移法的计算假定: a、忽略轴力产生的轴向变形的影响①杆件变形前的直线长=变形后的曲线长度

b、弯曲变形是微小,Q、(△)很少一②杆件变形后的曲线长度=弦线长度 例:DA、DB、△提、BAB、O ①②一推论1):尽管杆件产生弯曲变形,但直杆件两端(杆件两端)点之间的沿杆 的轴线方向的距离变形前后仍保持不变。也就是u=Ug:直杆两端的水平位移相等。 推论2):直杆的一端不变动而杆发生弯曲变形时,杆的另一端的线位移⊥杆原 轴线。 或两个不动点,引出两直杆的交点,也是不变动的。也就是u=u=0 c、略去剪切变形对位移的影响,剪切角Y=0 推论3):杆件轴挠曲线上某点之切线的倾角φ(与杆原轴线夹角)便是该点横 截面的转角。p=0+0=0 在力法中也有类似的假定,只不过当时未强调而已。 在超静定梁、刚架的位移系数计算时: 1)不考虑N引起的轴向变形三位移 2)不考虑Q引起的剪力变形一位移 3)小变形假设 由力法对于单跨静定梁,杆端M、Q(内力)是由荷载和(pA、PB、△、BAB 杆端位移所决定的。也就是它们之间存在有确定的关系,等截面直杆的转角位移方 程。 三、等截面直杆的转角位移方程 三种常见形式的单跨超静定梁:由荷载作用、温度变化、支座移动引起的杆端力可由力 法求得。一般→特殊 1、两端固定的梁: (1)受任意荷载作用(或温度变化): M。、M、Q、Q一一固端弯矩。(可由力法求得):表10-1。 (2)支座移动作用:pA、pB、△、(都假设为正):也可由力法求得 (3)pA、pB、△s和荷载共同作用下:由叠加原理: M=4ip+2ip。-6△4/+M Ma=4i+2i6+M (1) EI1杆件的线刚度。两端固定的单跨超静定梁转角位移方程。 注:也可用于刚架中有轴力的杆件。因为对于小挠度问题(小变形范围)可以不考虑N、 M之间的相互影响,也就是轴向变形和弯曲变形之间是相互独立的。 2、一端固定,一端铰支的单跨超静定梁 5
5 b、弯曲变形是微小,、(Δ)很少②杆件变形后的曲线长度=弦线长度 例:A、B、ΔAB、AB、 ①②推论 1):尽管杆件产生弯曲变形,但直杆件两端(杆件两端)点之间的沿杆 的轴线方向的距离变形前后仍保持不变。也就是 uA=uB;直杆两端的水平位移相等。 推论 2):直杆的一端不变动而杆发生弯曲变形时,杆的另一端的线位移⊥杆原 轴线。 或两个不动点,引出两直杆的交点,也是不变动的。也就是 uA=uB=0 c、略去剪切变形对位移的影响,剪切角γ=0 推论 3):杆件轴挠曲线上某点之切线的倾角(与杆原轴线夹角)便是该点横 截面的转角。=θ+r=θ 在力法中也有类似的假定,只不过当时未强调而已。 在超静定梁、刚架的位移系数计算时: 1)不考虑 N 引起的轴向变形位移 2)不考虑 Q 引起的剪力变形位移 3)小变形假设 由力法对于单跨静定梁,杆端 M、Q(内力)是由荷载和(A、B、ΔAB、AB 杆端位移所决定的。也就是它们之间存在有确定的关系,等截面直杆的转角位移方 程。 三、等截面直杆的转角位移方程 三种常见形式的单跨超静定梁:由荷载作用、温度变化、支座移动引起的杆端力可由力 法求得。一般 → 特殊 1、两端固定的梁: (1)受任意荷载作用(或温度变化): f M AB 、 f MBA 、 f QAB 、 f QBA——固端弯矩。(可由力法求得):表 10-1。 (2)支座移动作用: A、B、ΔAB、(都假设为正):也可由力法求得 (3)A、B、ΔAB和荷载共同作用下:由叠加原理: f AB AB A B l M AB i M i i + = 4 + 2 − 6 f AB BA B A l M BA i M i i + = 4 + 2 − 6 (1) i=EI/l 杆件的线刚度。两端固定的单跨超静定梁转角位移方程。 注:也可用于刚架中有轴力的杆件。因为对于小挠度问题(小变形范围)可以不考虑 N、 M 之间的相互影响,也就是轴向变形和弯曲变形之间是相互独立的。 2、一端固定,一端铰支的单跨超静定梁

(1)受任意荷载作用(或温度变化): M。、M、Qa、Q(可由力法求得):表10-1。 (2)支座移动作用:pA、△、(都假设为正):也可由力法求得 (3)pA、△和荷载共同作用下:由叠加原理: Mu-NeM MB4=0 (2) 也可由(1)式得: Mu=46+2ip,-6A/+M=0 解出ps,代入(1)式就可得(2)式。 3、一端固定,一端定向的单跨超静定梁: 同理可得: Man =ig-igg+M Ma =iga-io+MI (3) 注:①表中杆端内力是根据图示方向的位移方向和荷载情况求得的,当计算某一结构时, 应根据其杆件所受的实际位移方向和荷载情况,判断其杆端内力的正负号。 ②转角位移方程虽是针对单跨超静定梁(等截面)导出的,它们建立的关系对于刚架中 任何一根等截面受弯杆件来说都是适用的。 ③特殊情况:单位角位移或单位线位移下杆件内力图: §8-3位移法的基本未知量和基本结构 根据第一节的分析,我们知道:位移法是以一些结点位移作为基本未知量的,先求 这些位移,再求内力。 那么:到底以那些位移为基本未知量或位移法的基本未知量的数目如何确定呢? 要解决这个问题,首先应该从它的解题思路开始,我们先回顾一下位移法的基本思 路: 原结构(某些结点上加上一定的附加联系,把结点变成固定端或铰支) →基本结构(单跨超静定梁的组合体)再使各附加联系处发生与实际相符的位移。 位移法的基本未知量(当作外因) →原结构,所以根据基本结构在原荷载及这些结点位移共同作用下,在附加联系处 (上)产生的总约束力等于0的平衡条件 一建立位移法的典型方程 →求出这些结点位移未知量(以单跨静定梁的转角位移方程为基础)→最后内力。 显然,位移法的基本未知量数目指的是:原结构→基本结构(附加联系限制的位移
6 (1)受任意荷载作用(或温度变化): f M AB 、 f MBA 、 f QAB 、 f QBA (可由力法求得):表 10-1。 (2)支座移动作用: A、ΔAB、(都假设为正):也可由力法求得 (3)A、ΔAB和荷载共同作用下:由叠加原理: f AB A AB M AB l i M = i − + 3 3 MBA = 0 (2) 也可由(1)式得: 4 2 6 + = 0 = + − f AB BA B A l M BA i M i 解出B,代入(1)式就可得(2)式。 3、一端固定,一端定向的单跨超静定梁: 同理可得: f AB A B M AB M = i −i + f BA B A M BA M = i − i + (3) 注:①表中杆端内力是根据图示方向的位移方向和荷载情况求得的,当计算某一结构时, 应根据其杆件所受的实际位移方向和荷载情况,判断其杆端内力的正负号。 ②转角位移方程虽是针对单跨超静定梁(等截面)导出的,它们建立的关系对于刚架中 任何一根等截面受弯杆件来说都是适用的。 ③特殊情况:单位角位移或单位线位移下杆件内力图: §8-3 位移法的基本未知量和基本结构 根据第一节的分析,我们知道:位移法是以一些结点位移作为基本未知量的,先求 这些位移,再求内力。 那么:到底以那些位移为基本未知量或位移法的基本未知量的数目如何确定呢? 要解决这个问题,首先应该从它的解题思路开始,我们先回顾一下位移法的基本思 路: 原结构(某些结点上加上一定的附加联系,把结点变成固定端或铰支) →基本结构(单跨超静定梁的组合体)再使各附加联系处发生与实际相符的位移。 位移法的基本未知量(当作外因) →原结构,所以根据基本结构在原荷载及这些结点位移共同作用下,在附加联系处 (上)产生的总约束力等于 0 的平衡条件 →建立位移法的典型方程 →求出这些结点位移未知量(以单跨静定梁的转角位移方程为基础)→最后内力。 显然,位移法的基本未知量数目指的是:原结构→基本结构(附加联系限制的位移

数)或基本结构→原结构应放松的结点位移数。等于基本结构上所应具有的附加联系数 目。 所以:确定位移法基本未知量的数目可以和位移法的基本结构的选取联系起来。 例:一个门式刚架,所受荷载P、P2,(如何变形?) 原结构 变形 可能的变形:A、B固定端,无角位移和线位移,一般情况下,C、D应该各有三个 位移(水平、竖向线位移、角位移) 但,由位移法假定一→推论2可知:△=△w=0(竖向线位移等于0) C只沿⊥AC轴方向移动△。 D只沿⊥BD轴方向移动△。 由推论1:△=△=△ 所以C、D两点共有三个独立的位移pc、pD、△。要使原 结构→基本结构(三个单跨超静定梁的组合体)。也就是C、D 一固定端需加三个附加联系两个刚臂, 一个链杆,再使基本 结构→原结构(受力、变形等效) 应该在附加联系处强迫产生与实际相同的位移pC、p、 △(Z、Z2、Z2) 一、基本未知量: 包括:独立刚结点角位移: 独立的结点线位移。 确定位移法基本未知量的方法 1、刚结点的独立角位移=结构中刚结点的数目=附加刚臂的数目。 因为原结构凡属各杆相互刚结的每个刚结点均有一个独立的角位移,变成基本结构, 均需附加一个刚臂,所以只要数一下这种刚结点的数目即可: 2、独立的结点线位移数=附加链杆的数目。 要确定原结构→基本结构所需附加链杆的数目,主要依据为推论2:结构中两个不 动点所引出的不共线的两直杆相交的结点也是不动的。忽略受弯杆件的轴向变形,并认 >
7 数)或基本结构→原结构应放松的结点位移数。等于基本结构上所应具有的附加联系数 目。 所以:确定位移法基本未知量的数目可以和位移法的基本结构的选取联系起来。 例:一个门式刚架,所受荷载 P1、P2,(如何变形?) 原结构 变形 可能的变形:A、B 固定端,无角位移和线位移,一般情况下,C、D 应该各有三个 位移(水平、竖向线位移、角位移) 但,由位移法假定→推论 2 可知:ΔCV=ΔDV=0(竖向线位移等于 0) C 只沿⊥AC 轴方向移动ΔC D 只沿⊥BD 轴方向移动ΔD 由推论 1:ΔC=ΔD=Δ 所以 C、D 两点共有三个独立的位移 φC、φD、Δ。要使原 结构→基本结构(三个单跨超静定梁的组合体)。也就是 C、D →固定端需加三个附加联系两个刚臂,一个链杆,再使基本 结构→原结构(受力、变形等效) 应该在附加联系处强迫产生与实际相同的位移 φC、φD、 Δ(Z1、Z2、Z3 ) 一、基本未知量: 包括:独立刚结点角位移; 独立的结点线位移。 确定位移法基本未知量的方法 1、刚结点的独立角位移=结构中刚结点的数目=附加刚臂的数目。 因为原结构凡属各杆相互刚结的每个刚结点均有一个独立的角位移,变成基本结构, 均需附加一个刚臂,所以只要数一下这种刚结点的数目即可; 2、独立的结点线位移数=附加链杆的数目。 要确定原结构→基本结构所需附加链杆的数目,主要依据为推论 2:结构中两个不 动点所引出的不共线的两直杆相交的结点也是不动的。忽略受弯杆件的轴向变形,并认
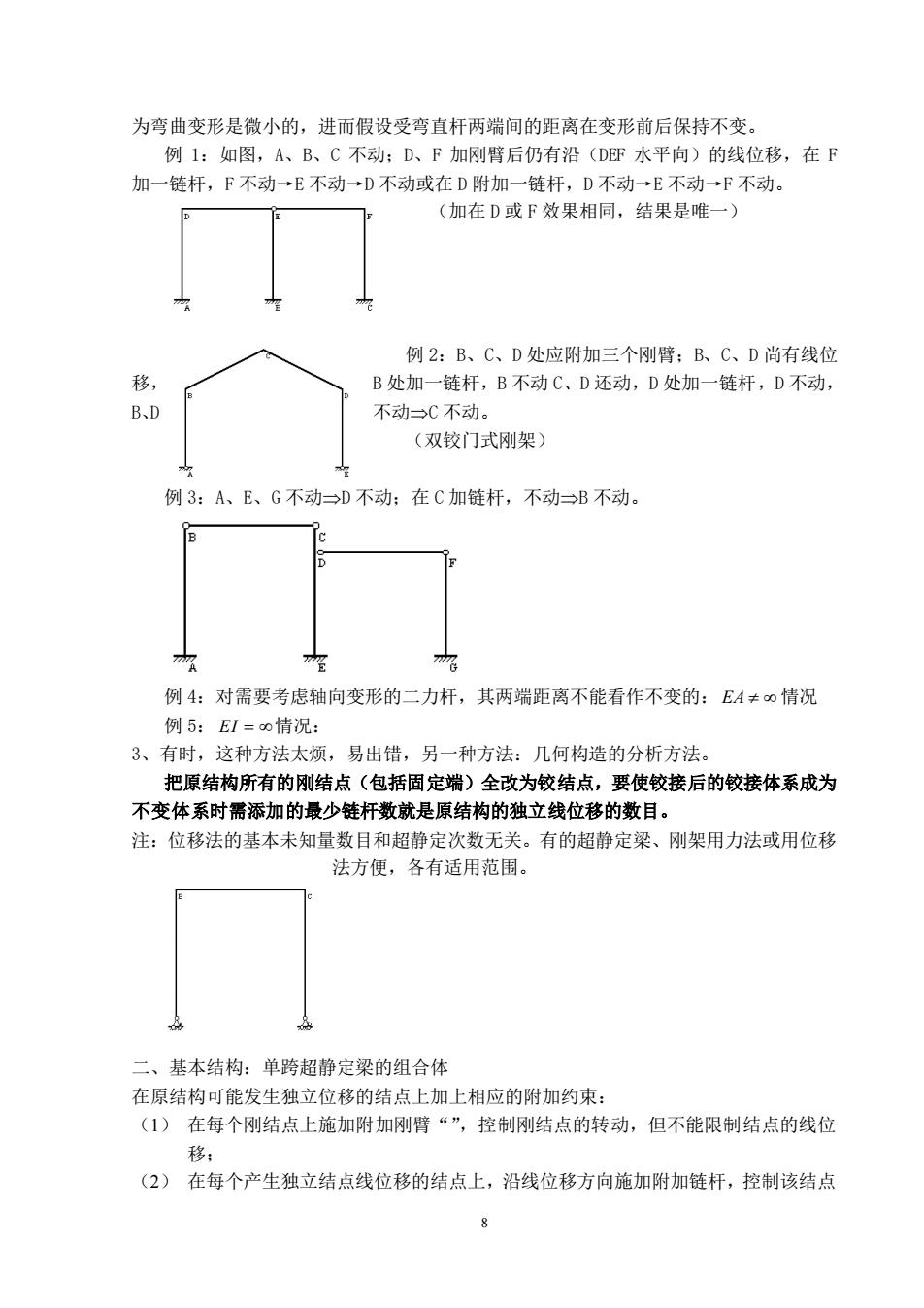
为弯曲变形是微小的,进而假设受弯直杆两端间的距离在变形前后保持不变 例1:如图,A、B、C不动:D、F加刚臂后仍有沿(DEF水平向)的线位移,在F 加一链杆,F不动一E不动一D不动或在D附加一链杆,D不动一E不动一F不动。 (加在D或F效果相同,结果是唯一) 例2:B、C、D处应附加三个刚臂:B、C、D尚有线位 移 B处加一链杆,B不动C、D还动,D处加一链杆,D不动, B、D 不动一C不动。 (双铰门式刚架) 例3:A、E、G不动→D不动:在C加链杆,不动一B不动。 例4:对需要考虑轴向变形的二力杆,其两端距离不能看作不变的:EA≠∞情况 例5:E1=o情况: 3、有时,这种方法太烦,易出错,另一种方法:几何构造的分析方法。 把原结构所有的刚结点(包括固定端)全改为铰结点,要使铰接后的铰接体系成为 不变体系时需添加的最少链杆数就是原结构的独立线位移的数目。 注:位移法的基本未知量数目和超静定次数无关。有的超静定梁、刚架用力法或用位移 法方便,各有适用范围。 二、基本结构:单跨超静定梁的组合体 在原结构可能发生独立位移的结点上加上相应的附加约束: (1)在每个刚结点上施加附加刚臂“”,控制刚结点的转动,但不能限制结点的线位 移: (2)在每个产生独立结点线位移的结点上,沿线位移方向施加附加链杆,控制该结点
8 为弯曲变形是微小的,进而假设受弯直杆两端间的距离在变形前后保持不变。 例 1:如图,A、B、C 不动;D、F 加刚臂后仍有沿(DEF 水平向)的线位移,在 F 加一链杆,F 不动→E 不动→D 不动或在 D 附加一链杆,D 不动→E 不动→F 不动。 (加在 D 或 F 效果相同,结果是唯一) 例 2:B、C、D 处应附加三个刚臂;B、C、D 尚有线位 移, B 处加一链杆,B 不动 C、D 还动,D 处加一链杆,D 不动, B、D 不动C 不动。 (双铰门式刚架) 例 3:A、E、G 不动D 不动;在 C 加链杆,不动B 不动。 例 4:对需要考虑轴向变形的二力杆,其两端距离不能看作不变的: EA 情况 例 5: EI = 情况: 3、有时,这种方法太烦,易出错,另一种方法:几何构造的分析方法。 把原结构所有的刚结点(包括固定端)全改为铰结点,要使铰接后的铰接体系成为 不变体系时需添加的最少链杆数就是原结构的独立线位移的数目。 注:位移法的基本未知量数目和超静定次数无关。有的超静定梁、刚架用力法或用位移 法方便,各有适用范围。 二、基本结构:单跨超静定梁的组合体 在原结构可能发生独立位移的结点上加上相应的附加约束: (1) 在每个刚结点上施加附加刚臂“”,控制刚结点的转动,但不能限制结点的线位 移; (2) 在每个产生独立结点线位移的结点上,沿线位移方向施加附加链杆,控制该结点
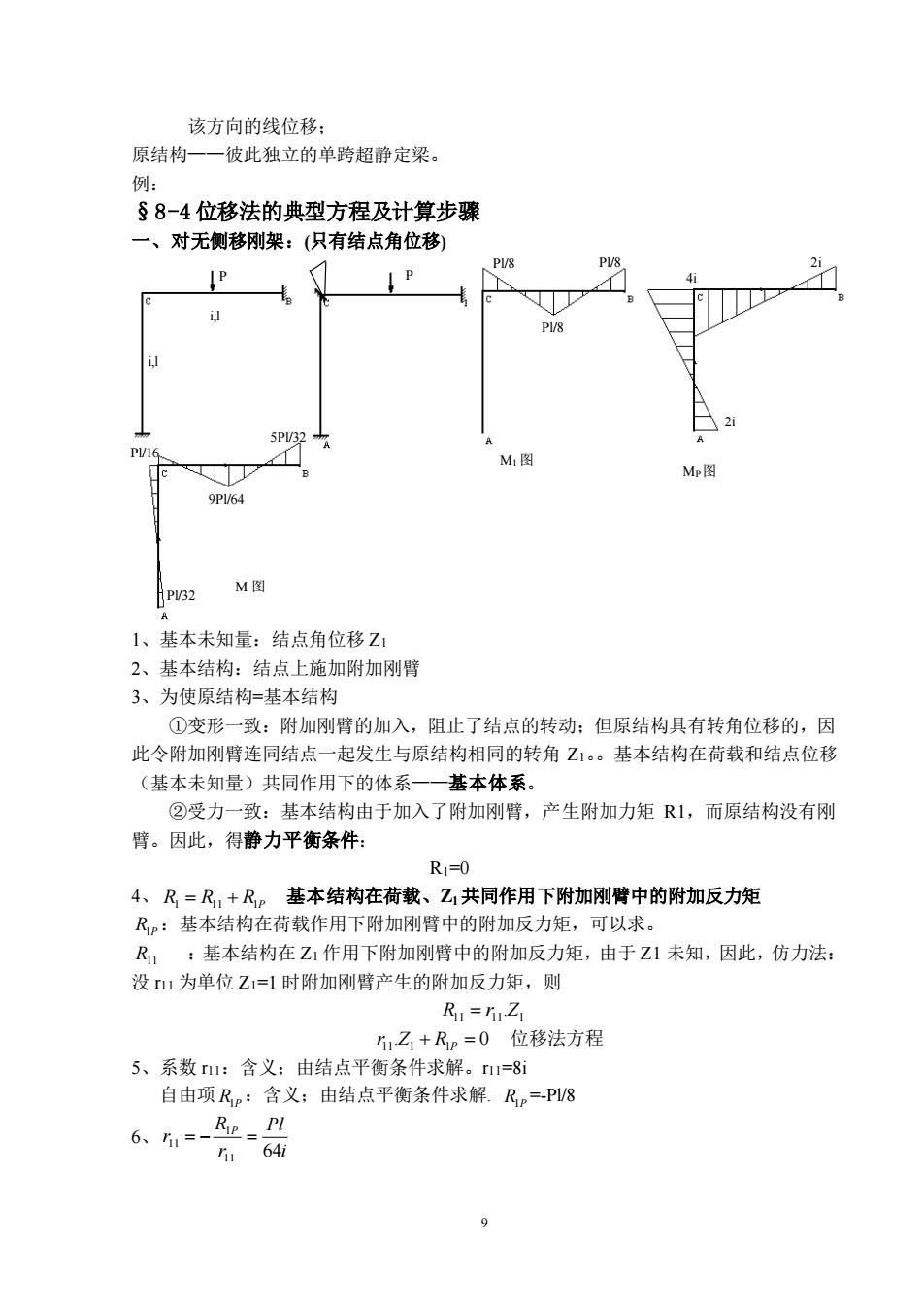
该方向的线位移: 原结构一一彼此独立的单跨超静定梁。 例: §8-4位移法的典型方程及计算步骤 一、对无侧移刚架:(只有结点角位移) P P il M图 Mr图 9PI/64 M图 1、基本未知量:结点角位移Z1 2、基本结构:结点上施加附加刚臂 3、为使原结构-基本结构 ①变形一致:附加刚臂的加入,阻止了结点的转动:但原结构具有转角位移的,因 此令附加刚臂连同结点一起发生与原结构相同的转角Z1。基本结构在荷载和结点位移 (基本未知量)共同作用下的体系一一基本体系。 ②受力一致:基本结构由于加入了附加刚臂,产生附加力矩R1,而原结构没有刚 臂。因此,得静力平衡条件 R1=0 4、R=R,+R。基本结构在荷载、Z共同作用下附加刚臂中的附加反力矩 R。:基本结构在荷载作用下附加刚中的附加反力矩,可以求。 R,:基本结构在Z1作用下附加刚臂中的附加反力矩,由于Z1未知,因此,仿力法: 没1为单位Z1=1时附加刚臂产生的附加反力矩,则 R=Z 1乙+Rp=0位移法方程 5、系数1:含义:由结点平衡条件求解。1=8i 自由项Rp:含义:由结点平衡条件求解.Re=PV8 5164 9
9 该方向的线位移; 原结构——彼此独立的单跨超静定梁。 例: §8-4 位移法的典型方程及计算步骤 一、对无侧移刚架:(只有结点角位移) 1、基本未知量:结点角位移 Z1 2、基本结构:结点上施加附加刚臂 3、为使原结构=基本结构 ①变形一致:附加刚臂的加入,阻止了结点的转动;但原结构具有转角位移的,因 此令附加刚臂连同结点一起发生与原结构相同的转角 Z1。基本结构在荷载和结点位移 (基本未知量)共同作用下的体系——基本体系。 ②受力一致:基本结构由于加入了附加刚臂,产生附加力矩 R1,而原结构没有刚 臂。因此,得静力平衡条件: R1=0 4、 R1 = R11 + R1P 基本结构在荷载、Z1共同作用下附加刚臂中的附加反力矩 R1P :基本结构在荷载作用下附加刚臂中的附加反力矩,可以求。 R11 :基本结构在 Z1 作用下附加刚臂中的附加反力矩,由于 Z1 未知,因此,仿力法: 没 r11 为单位 Z1=1 时附加刚臂产生的附加反力矩,则 11 11 1 R = r .Z r11.Z1 + R1P = 0 位移法方程 5、系数 r11:含义;由结点平衡条件求解。r11=8i 自由项 R1P :含义;由结点平衡条件求解. R1P =-Pl/8 6、 i Pl r R r P 11 64 1 11 = − = 基本结构 P i,l i,l P Pl/8 Pl/8 Pl/8 4i 2i 2i MP图 M1图 Pl/16 5Pl/32 Pl/32 9Pl/64 M 图

7、M=MZ,+Mp 二、有侧移刚架:结点角位移+结点线位移 1、本未知量:结点角位移Z1.结点线位移Z2 2、基本结构:结点上施加附加刚臂、附加链杆 3、为使原结构=基本结构 ①变形一致:附加刚臂、链杆的加入,阻止了结点的转动、移动:但原结构具有转 角位移、线位移的,因此令附加刚臂连同结点一起发生与原结构相同的转角Z,附加链 杆连同结点一起发生与原结构相同的线位移Z2。基本结构在荷载和结点位移(基本未 知量)共同作用下的体系一一基本体系。 ②受力一致:基本结构由于加入了附加刚臂、附加链杆,产生附加力矩R1、附加 反力R2,而原结构没有刚臂、链杆。因此,得静力平衡条件: R1=0 R2=0 4、R=R,+R,+Rp=0基本结构在荷载、Z、Z共同作用下附加刚臂中附加反力矩 R2=R1+R2+R2P=0基本结构在荷载、Z、Z共同作用下附加链杆中附加反力 R、RP:基本结构在荷载作用下附加刚臂、附加链杆中的附加反力矩、附加反力,可 以求。 R,、R2:基本结构在Z1、Z2作用下附加刚臂中的附加反力矩,由于Z1未知,因 此,仿力法:R=1乙R:=乙 同理:R1=21ZR2=2Z2 51Z,+52Z2+RP=0 10
10 7、 M = M1Z1 + M P 二、有侧移刚架:结点角位移+结点线位移 1、本未知量:结点角位移 Z1、结点线位移 Z2 2、基本结构:结点上施加附加刚臂、附加链杆 3、为使原结构=基本结构 ①变形一致:附加刚臂、链杆的加入,阻止了结点的转动、移动;但原结构具有转 角位移、线位移的,因此令附加刚臂连同结点一起发生与原结构相同的转角 Z1,附加链 杆连同结点一起发生与原结构相同的线位移 Z2。基本结构在荷载和结点位移(基本未 知量)共同作用下的体系——基本体系。 ②受力一致:基本结构由于加入了附加刚臂、附加链杆,产生附加力矩 R1、附加 反力 R2,而原结构没有刚臂、链杆。因此,得静力平衡条件: R1=0 R2=0 4、 R1 = R11 + R12 + R1P = 0 基本结构在荷载、Z1、Z2共同作用下附加刚臂中附加反力矩 R2 = R21 + R22 + R2P = 0 基本结构在荷载、Z1、Z2共同作用下附加链杆中附加反力 R1P、R2P :基本结构在荷载作用下附加刚臂、附加链杆中的附加反力矩、附加反力,可 以求。 R11、 R12 :基本结构在 Z1、Z2 作用下附加刚臂中的附加反力矩,由于 Z1 未知,因 此,仿力法: 11 11 1 R = r .Z 12 12 2 R = r .Z 同理: 21 21 1 R = r .Z 22 22 2 R = r .Z r11.Z1 + r12Z2 + R1P = 0