
第六章弯曲应力 ⊙嘉道大辜
第六章 弯曲应力

第六章弯曲应力 §6-1引言 §6-2弯曲正应力 §6-3弯曲切应力 §6-4梁的强度条件 §6-5梁的合理强度设计 §6-6双对称截面梁的非对称弯曲
第六章 弯曲应力 §6-1 引言 §6-2 弯曲正应力 §6-3 弯曲切应力 §6-4 梁的强度条件 §6-5 梁的合理强度设计 §6-6 双对称截面梁的非对称弯曲
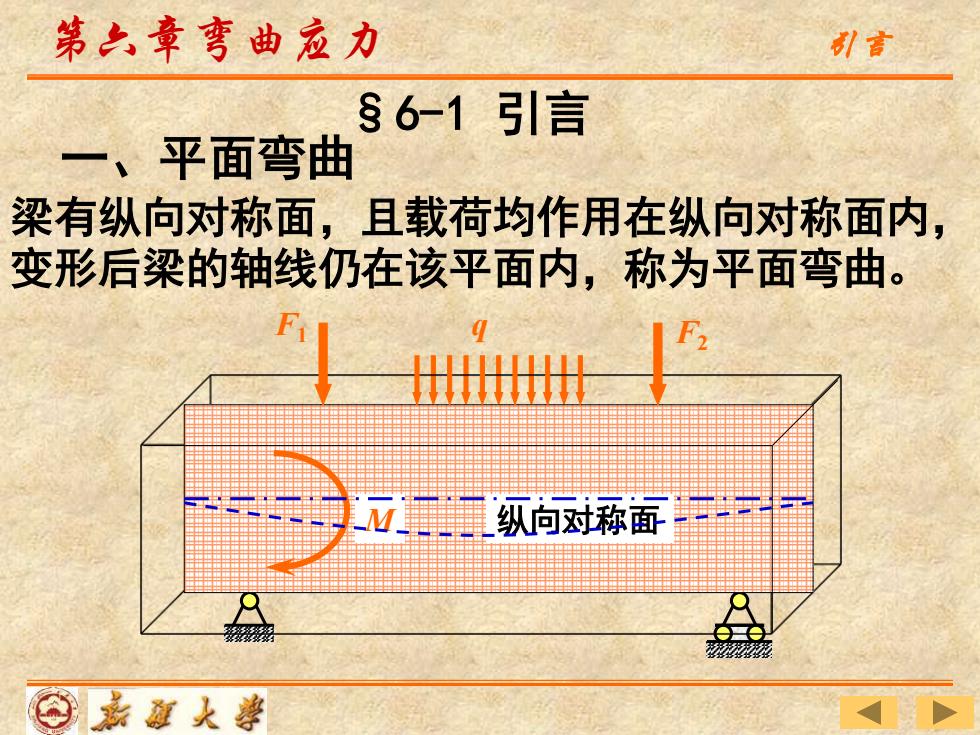
第之章弯曲应力 刊言 §6-1引言 一、平面弯 梁有纵向对称面,且载荷均作用在纵向对称面内, 变形后梁的轴线仍在该平面内,称为平面弯曲。 F F2 一真颈向对森面备 ⊙嘉道大事
M 纵向对称面 F1 F2 q 一、平面弯曲 §6-1 引言 梁有纵向对称面,且载荷均作用在纵向对称面内, 变形后梁的轴线仍在该平面内,称为平面弯曲。 第六章弯曲应力 引言
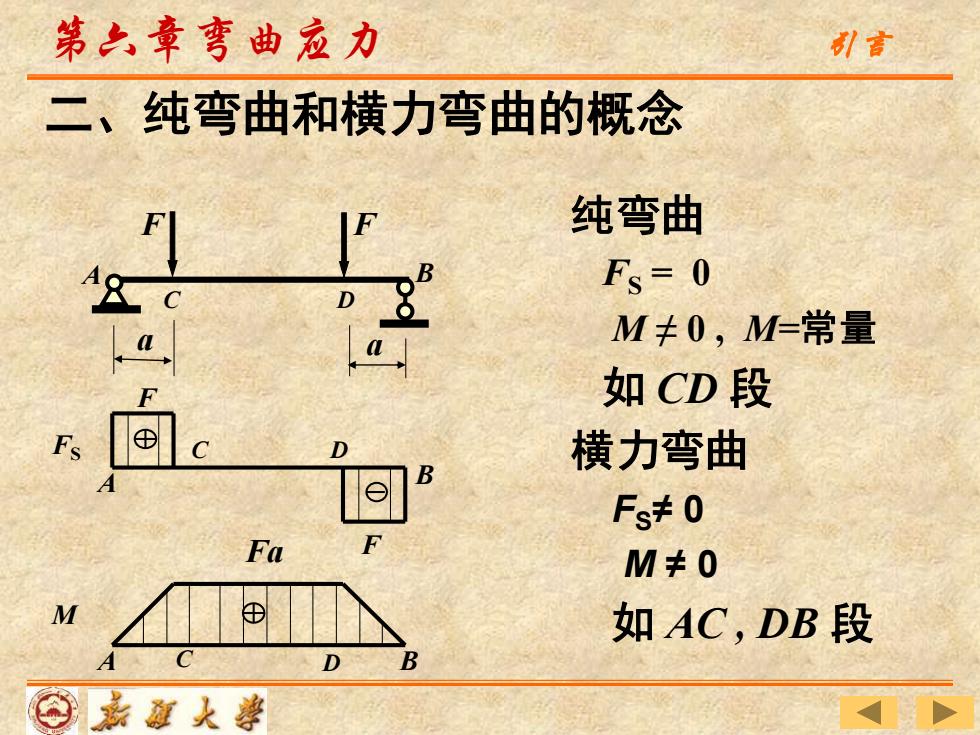
第六章弯曲应力 升言 二、纯弯曲和横力弯曲的概念 纯弯曲 Fs=0 M≠0,M=常量 如CD段 横力弯曲 Fs≠0 Fa M≠0 M 如AC,DB段 A D ⊙嘉道人導
纯弯曲 FS = 0 M ≠ 0 , M=常量 如 CD 段 横力弯曲 FS≠ 0 M ≠ 0 如 AC , DB 段 a F F C D B a A 二、纯弯曲和横力弯曲的概念 Fa M A C D B F F A C D B FS 第六章弯曲应力 引言
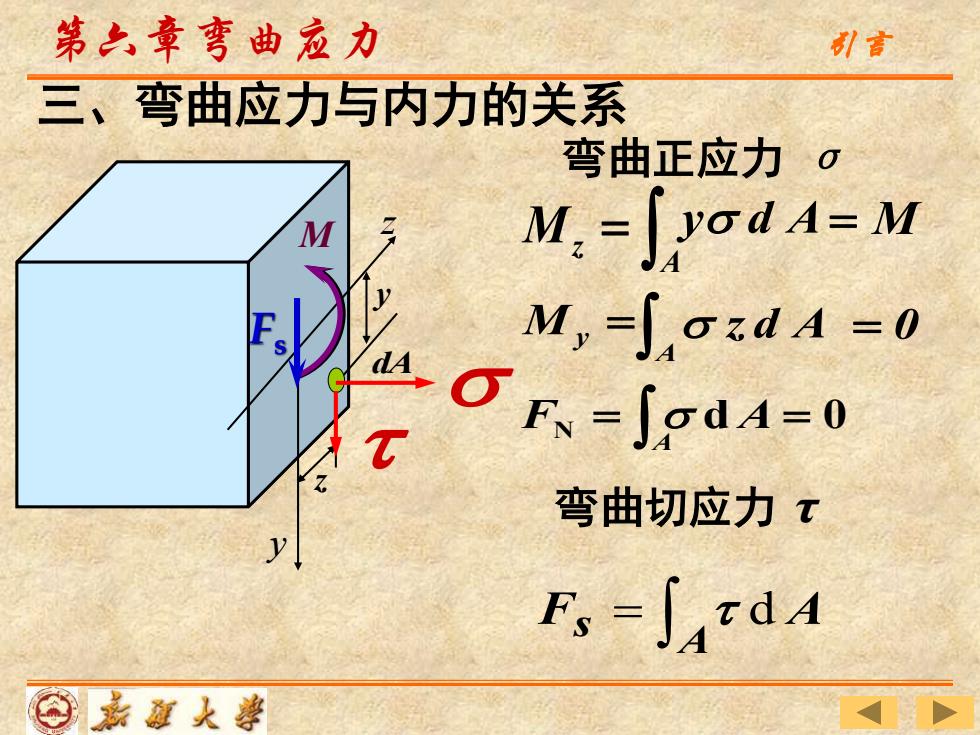
第之章弯曲应力 升言 三、弯曲应力与内力的关系 弯曲正应力 M 山,=∫oaA=M M,=∫ozdA=0 OFs-J9dd-0 弯曲切应力x Fs=JatdA 百嘉火事
三、弯曲应力与内力的关系 弯曲正应力 σ y z N = d = 0 A F A A z d A y d A = A Fs d A 弯曲切应力 τ 第六章弯曲应力 M y z dA Fs = A Mz = M 引言 My = = 0
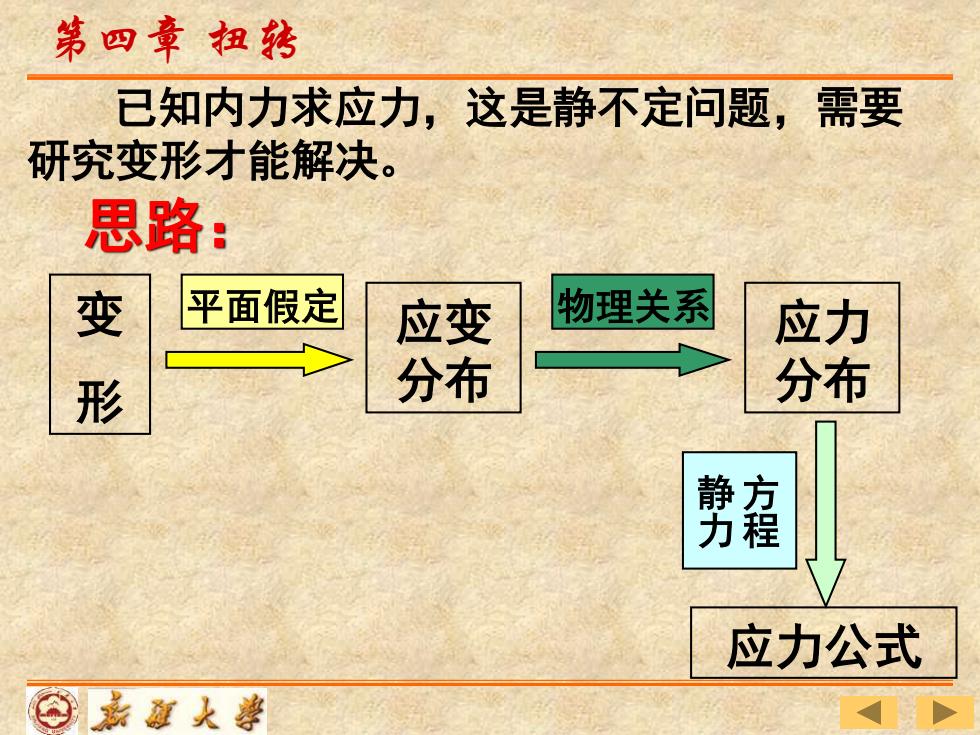
第四章扭转 已知内力求应力,这是静不定问题,需要 研究变形才能解决。 思路: 变 平面假定 应变 物理关系 应力 分布 分布 第容 应力公式 ⊙嘉道人善
思路: 第四章 扭转 变 形 应变 分布 平面假定 物理关系 应力 分布 应力公式 方 程 静 力 已知内力求应力,这是静不定问题,需要 研究变形才能解决
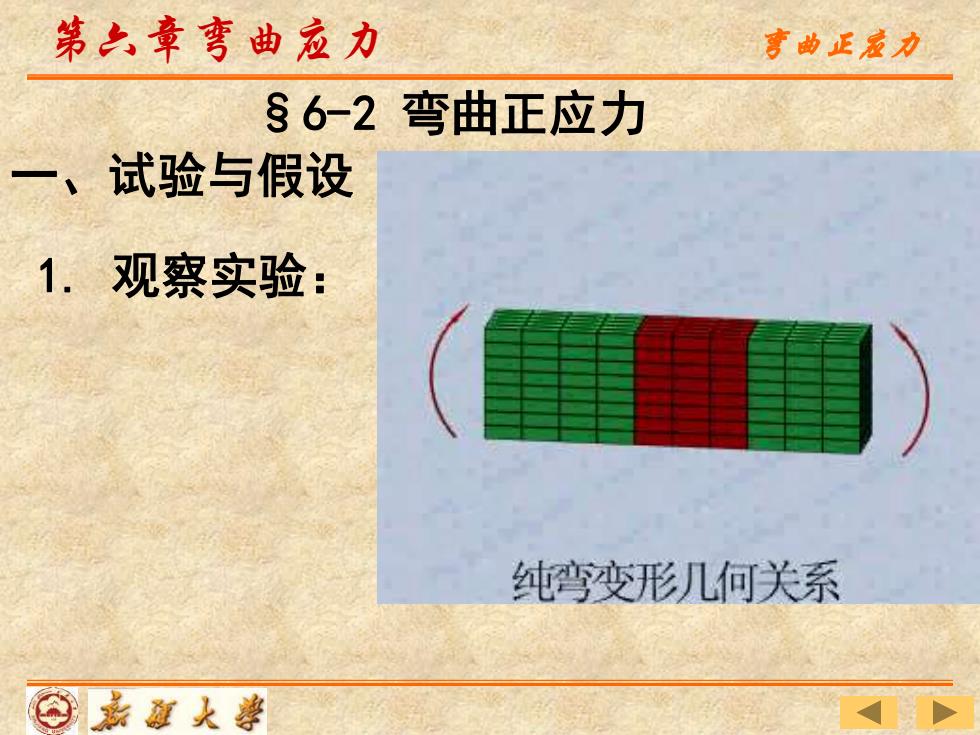
第六章弯曲应力 亨曲正宝力 §6-2 弯曲正应力 一、试验与假设 1.观察实验: 纯弯变形几何关系 百嘉道火事
一、试验与假设 1. 观察实验: §6-2 弯曲正应力 第六章弯曲应力 弯曲正应力
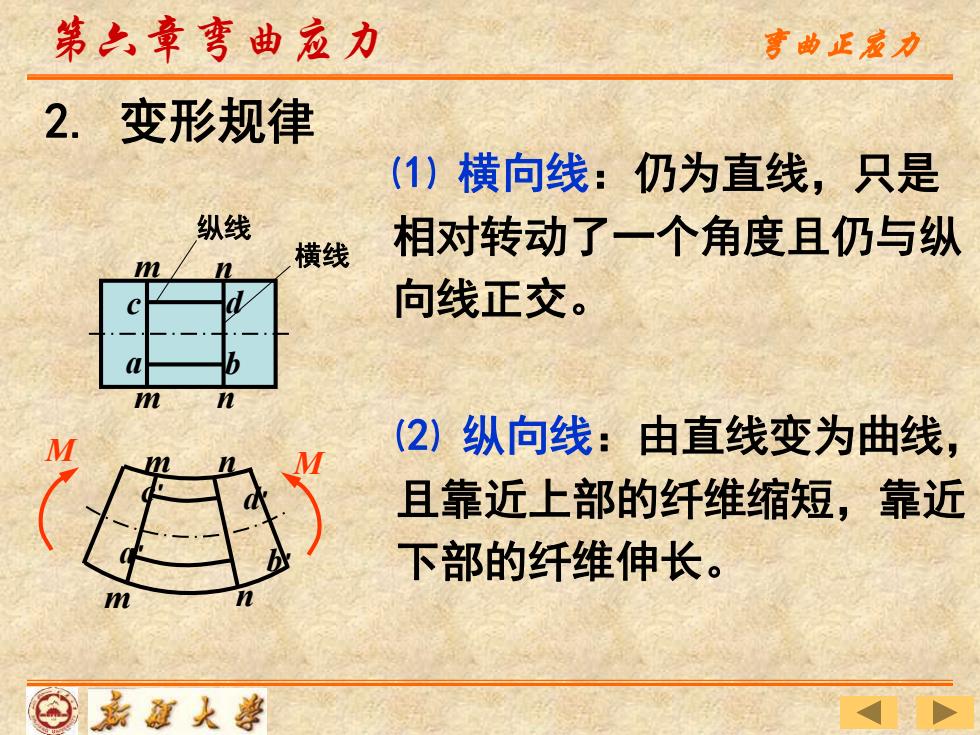
第六章弯曲应力 亨曲正宏力 2.变形规律 (1)横向线:仍为直线,只是 纵线 横线 相对转动了一个角度且仍与纵 向线正交。 (2)纵向线:由直线变为曲线, 且靠近上部的纤维缩短,靠近 下部的纤维伸长。 ⊙嘉面人善
d a m b 横线 纵线 m n n c 2. 变形规律 ⑴ 横向线:仍为直线,只是 相对转动了一个角度且仍与纵 向线正交。 ⑵ 纵向线:由直线变为曲线, 且靠近上部的纤维缩短,靠近 下部的纤维伸长。 m m n n c′ a′ b′ M M d′ 第六章弯曲应力 弯曲正应力
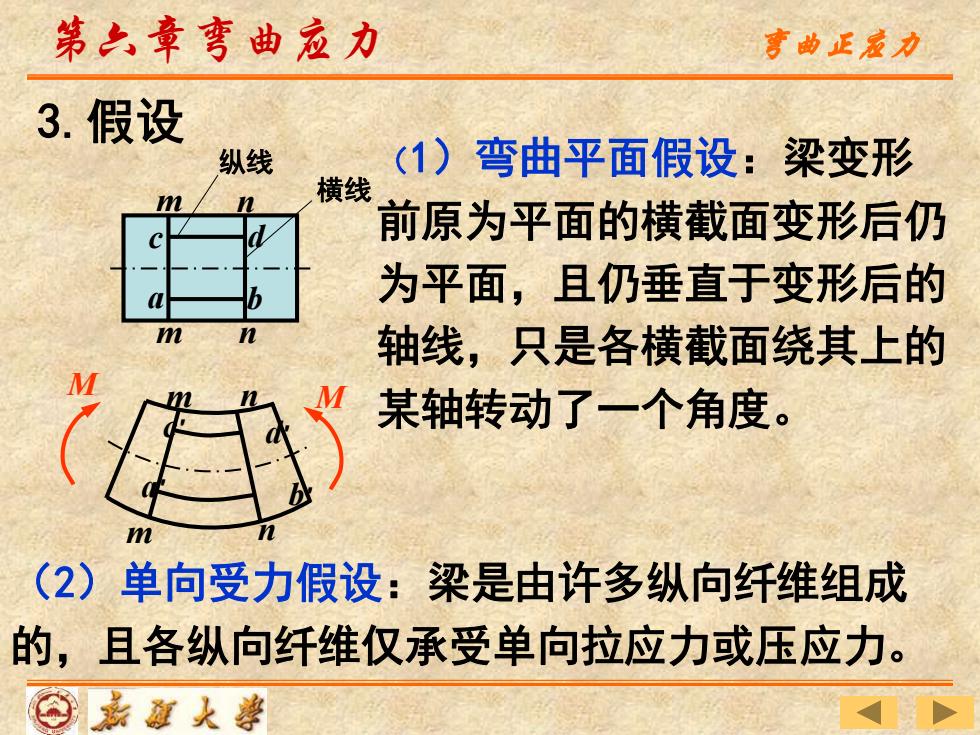
第六章弯曲应力 弯曲正家力 3.假设 纵线 (1)弯曲平面假设:梁变形 横线 前原为平面的横截面变形后仍 为平面,且仍垂直于变形后的 轴线,只是各横截面绕其上的 某轴转动了一个角度。 m (2)单向受力假设:梁是由许多纵向纤维组成 的,且各纵向纤维仅承受单向拉应力或压应力。 ⊙嘉道大¥
d a m b 横线 纵线 m n n c 3.假设 (1)弯曲平面假设:梁变形 前原为平面的横截面变形后仍 为平面,且仍垂直于变形后的 轴线,只是各横截面绕其上的 某轴转动了一个角度。 (2)单向受力假设:梁是由许多纵向纤维组成 的,且各纵向纤维仅承受单向拉应力或压应力。 m m n n c′ a′ b′ M M d′ 第六章弯曲应力 弯曲正应力
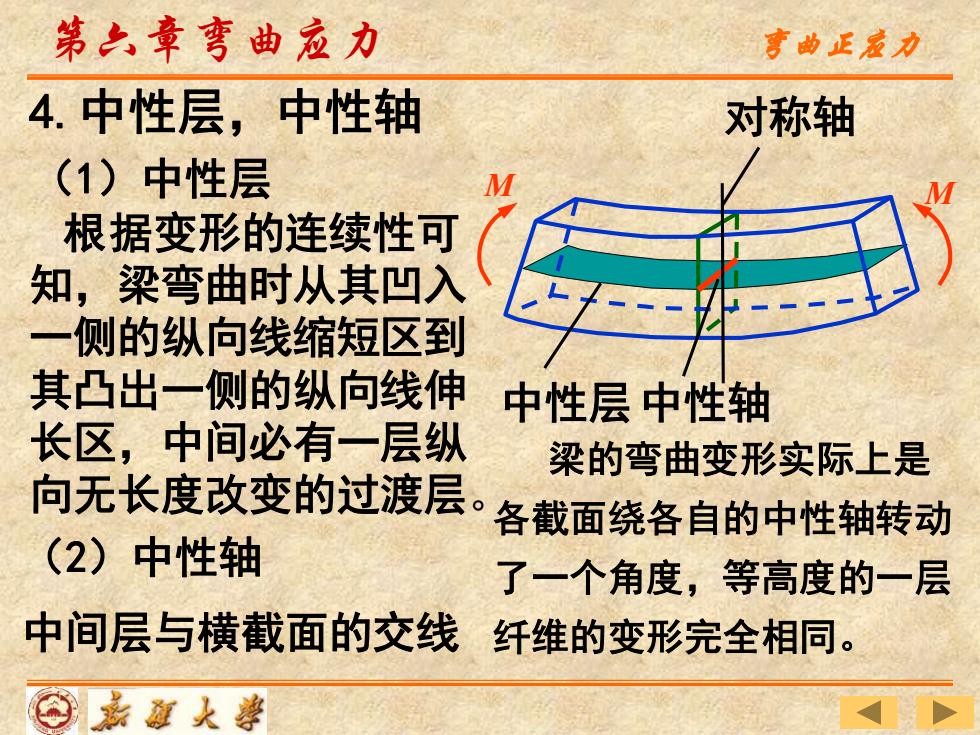
第之章弯曲应力 弯曲正京力 4.中性层,中性轴 对称轴 (1)中性层 M 根据变形的连续性可 知,梁弯曲时从其凹入 一侧的纵向线缩短区到 其凸出一侧的纵向线伸 中性层中性轴 长区,中间必有一层纵 梁的弯曲变形实际上是 向无长度改变的过渡层。 各截面绕各自的中性轴转动 (2)中性轴 了一个角度,等高度的一层 中间层与横截面的交线 纤维的变形完全相同
根据变形的连续性可 知,梁弯曲时从其凹入 一侧的纵向线缩短区到 其凸出一侧的纵向线伸 长区,中间必有一层纵 向无长度改变的过渡层。 中间层与横截面的交线 梁的弯曲变形实际上是 各截面绕各自的中性轴转动 了一个角度,等高度的一层 纤维的变形完全相同。 第六章弯曲应力 4.中性层,中性轴 (1)中性层 (2)中性轴 弯曲正应力 M M 中性层中性轴 对称轴