
弯曲变形 典型习题解析 1试用积分法写出图示梁的挠曲轴方程,说明用什么条件决定方程中积分常数,画出挠曲 轴大致形状。图中C为中间铰。EI为己知。 解题分析:梁上中间铰处,左、右挠度相等,转角 不相等。 解:设支反力为F,、M小F8,如图示。 1、建立各段挠曲轴近似微分方程并积分 题1图 将梁分为AC、CB、BD段 AC段0≤x1sa 挠曲轴近似微分方程E1=MA~Fa,x1 转角方程1m=M1-C (a) 挠度方程E1m,M,i.F+C+D b 2 6 CB段a≤x2s(a+b) 挠曲轴近似微分方程E1:=MA~Fyx2 转角方程E1时=M4,-F,3+C: (c) 2 挠度方程E1m1-Mi.5。+C西+D, 6 (d) BD段(a+b)sx3≤ 挠曲轴近似微分方程EIw=MA-F+FB,-(口+b) 转角方程E1=M4x3-2 FyFatc (e) 度方程,.F过,P-a+,C+0 6 2、确定积分常数 共有C、D、C、D、CD,6个积分常数。需要6个位移边界条件和光滑连续条 件
弯曲变形 典型习题解析 1 试用积分法写出图示梁的挠曲轴方程,说明用什么条件决定方程中积分常数,画出挠曲 轴大致形状。图中 C 为中间铰。 E I 为已知。 w 解题分析:梁上中间铰处,左、右挠度相等,转角 不相等。 解:设支反力为 F A y 、M A、F B y ,如图示。 1、建立各段挠曲轴近似微分方程并积分 将梁分为 AC、CB、BD 段。 AC 段 0 ≤ x 1 ≤ a 挠曲轴近似微分方程 1 1 E I w M F x A A y ′′ = − ⋅ 转角方程 1 2 1 1 ' 1 2 C F x E I w M x A y = A − + (a) 挠度方程 1 1 1 3 1 2 1 1 2 6 C x D M x F x E I w A A y = − + + (b) CB 段 ( ) a ≤ x 2 ≤ a + b 挠曲轴近似微分方程 2 " 2 E I w M F x A A y = − ⋅ 转角方程 2 2 2 2 2 2 C F x E I w M x A y ′ = A − + (c) 挠度方程 2 2 2 3 2 2 2 2 2 6 C x D M x F x E I w A A y = − + + (d) BD 段 a + b ≤ x ≤ l 3 ( ) 挠曲轴近似微分方程 [ ( )] 3 3 3 E I w M F x F x a b ′′ = A − A y + B y − + 转角方程 [ ] 3 2 3 2 3 3 3 2 ( ) 2 C F x F x a b E I w M x A y B y A + − + ′ = − + (e) 挠度方程 [ ] 3 3 3 3 3 3 3 2 3 3 6 ( ) 2 6 C x D M x F x F x a b E I w A A y B y + + − + = − + (f) 2、确定积分常数 共有 6 个积分常数。需要 6 个位移边界条件和光滑连续条 件。 C1 、D1、C2、D2、C3、D3 题 1 图 FAy l A B C b F MA D x a FBy 1
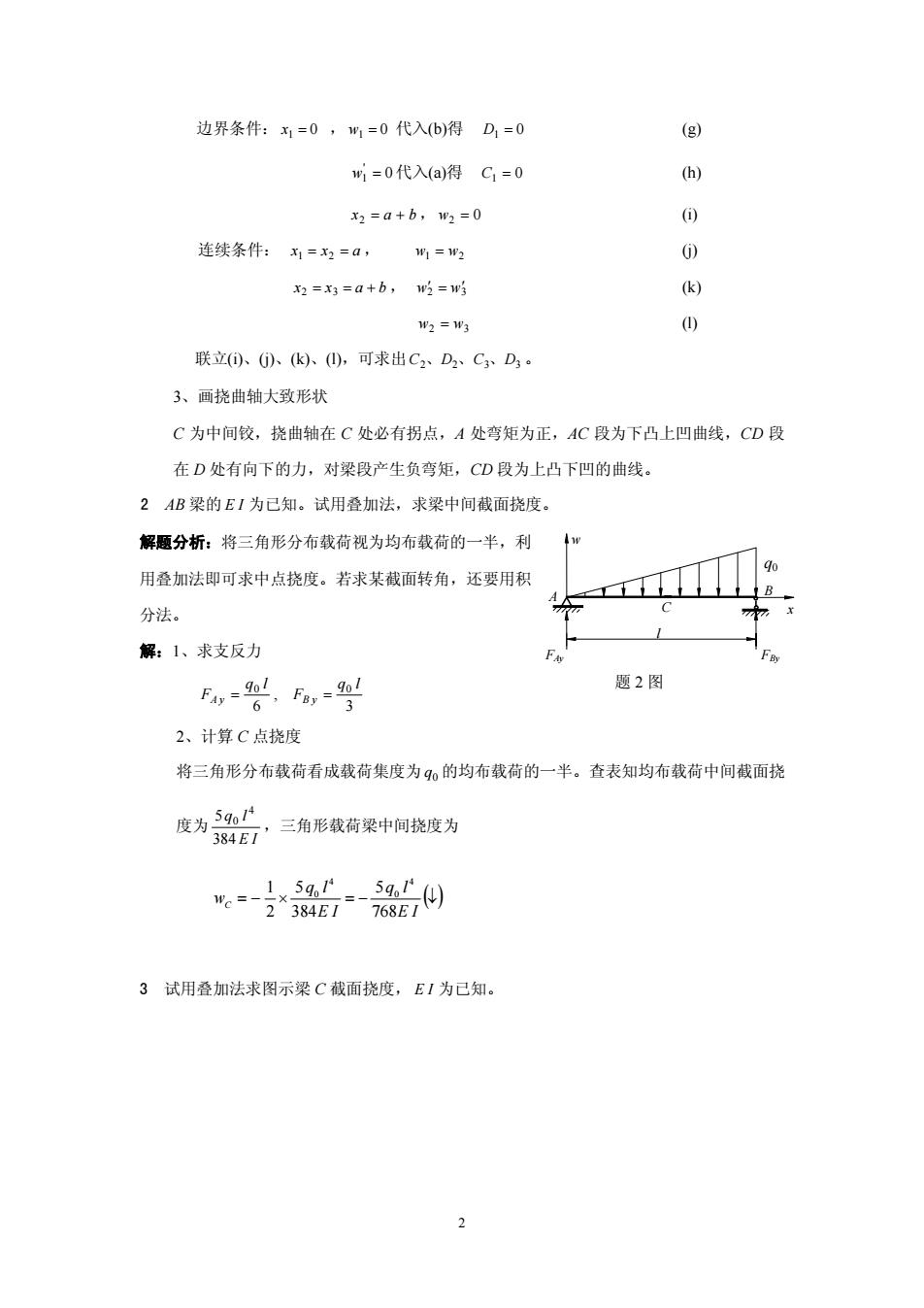
边界条件:x1=0,M=0代入(b)得D,=0 (g) i=0代入(a)得C=0 2=a+b,w2=0 连续条件:=x=a, 期1=w3 ==a+b,w时=w5 2=13 联立(0、k、山,可求出C2、D2、CD 3、画挠曲轴大致形状 C为中间铰,挠曲轴在C处必有拐点,A处弯矩为正,AC段为下凸上凹曲线,CD段 在D处有向下的力,对梁段产生负弯矩,CD段为上凸下凹的曲线。 2AB梁的E1为已知。试用叠加法,求梁中间截面挠度 解题分析:将三角形分布载荷视为均布载荷的一半,利 用叠加法即可求中点挠度。若求某截面转角,还要用积 分法。 解:1、求支反力 Fiy-.Fay 题2图 2、计算C点挠度 将三角形分布载荷看成载荷集度为q的均布载荷的一半。查表知均布载荷中间截面挠 度为三角形有奖中同度为 =0站00 3试用叠加法求图示梁C截面挠度,E1为已知
边界条件: 0 , 代入(b)得 x1 = w1 = 0 D1 = 0 (g) 0 ' w1 = 代入(a)得 C1 = 0 (h) x2 = a + b , w2 = 0 (i) 连续条件: x = x = a , 1 2 w1 = w2 (j) x2 = x3 = a + b , w2 w3 ′ = ′ (k) w2 = w3 (l) 联立(i)、(j)、(k)、(l),可求出C2、D2、C3、D3 。 3、画挠曲轴大致形状 C 为中间铰,挠曲轴在 C 处必有拐点,A 处弯矩为正,AC 段为下凸上凹曲线,CD 段 在 D 处有向下的力,对梁段产生负弯矩,CD 段为上凸下凹的曲线。 2 AB 梁的 E I 为已知。试用叠加法,求梁中间截面挠度。 解题分析:将三角形分布载荷视为均布载荷的一半,利 w 用叠加法即可求中点挠度。若求某截面转角,还要用积 分法。 q0 B A 解:1、求支反力 3 , 6 0 0 q l F q l FA y = B y = 2、计算 C 点挠度 将三角形分布载荷看成载荷集度为 的均布载荷的一半。查表知均布载荷中间截面挠 度为 q0 E I q l 384 5 4 0 ,三角形载荷梁中间挠度为 = − × = − (↓) E I q l E I q l wC 768 5 384 5 2 1 4 0 4 0 3 试用叠加法求图示梁 C 截面挠度, E I 为已知。 FAy FBy 题 2 图 l C x 2
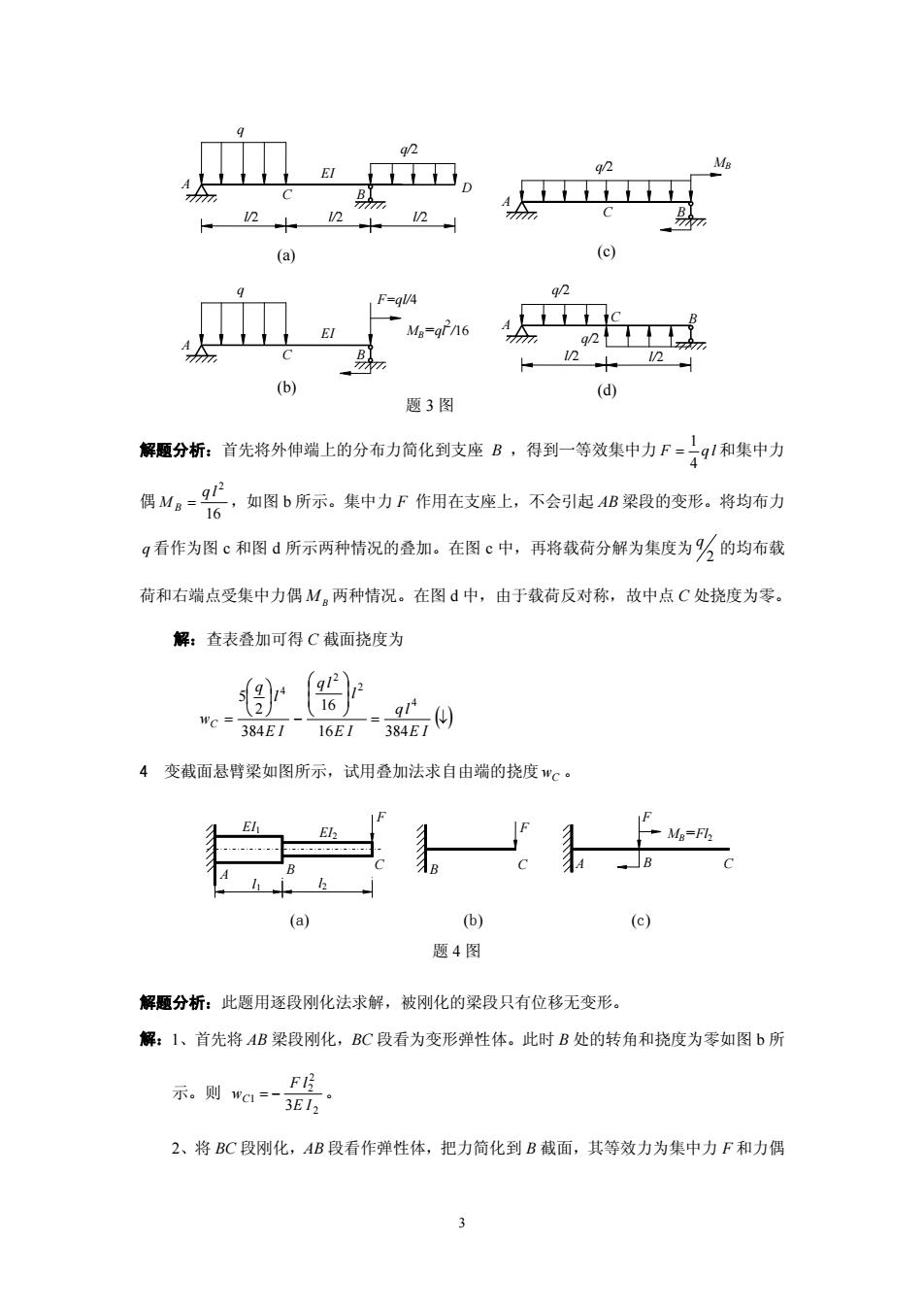
2 2 2 2 西 (a) (c) F-qla Me=gn6 人 题3图 解题分析:首先将外伸端上的分布力简化到支座B,得到一等效集中力F=91和集中力 偶M。一代,如图6所示。集中力F作用在支座上,不会引虑侣果段的支形,将均布力 g看作为图c和图d所示两种情祝的叠加。在图c中,再将载荷分解为集度为的均布载 荷和右端点受集中力偶M两种情况。在图d中,由于载荷反对称,故中点C处挠度为零。 解:查表叠加可得C截面挠度为 ( 4变截面悬臂梁如图所示,试用叠加法求自由端的挠度"℃。 (a) (b) (c) 题4图 解题分析:此题用逐段刚化法求解,被刚化的梁段只有位移无变形。 解:【、首先将AB梁段刚化,BC段看为变形弹性体。此时B处的转角和挠度为零如图b所 示.则a=3E 2、将BC段刚化,AB段看作弹性体,把力简化到B截面,其等效力为集中力F和力偶 3
q 解题分析:首先将外伸端上的分布力简化到支座 B ,得到一等效集中力 F q l 4 1 = 和集中力 偶 16 2 q l M B = ,如图 b 所示。集中力 F 作用在支座上,不会引起 AB 梁段的变形。将均布力 q 看作为图 c 和图 d 所示两种情况的叠加。在图 c 中,再将载荷分解为集度为 2 q 的均布载 荷和右端点受集中力偶 MB 两种情况。在图 d 中,由于载荷反对称,故中点 C 处挠度为零。 解:查表叠加可得 C 截面挠度为 = (↓) ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = E I q l E I l q l E I l q wC 16 384 16 384 2 5 4 2 2 4 4 变截面悬臂梁如图所示,试用叠加法求自由端的挠度 wC 。 解题分析:此题用逐段刚化法求解,被刚化的梁段只有位移无变形。 解:1、首先将 AB 梁段刚化,BC 段看为变形弹性体。此时 B 处的转角和挠度为零如图 b 所 示。则 2 2 2 1 3E I F l wC = − 。 2、将 BC 段刚化,AB 段看作弹性体,把力简化到 B 截面,其等效力为集中力 F 和力偶 B A F EI2 EI1 A C B (a) (b) (c) 题 4 图 l1 l2 C F B C F MB=Fl2 B EI C B (a) q F=ql/4 A q/2 EI MB l/2 l/2 l/2 l/2 l/2 题 3 图 MB=ql2 /16 q/2 (d) A q/2 C B (c) D A q/2 C B A C (b) 3
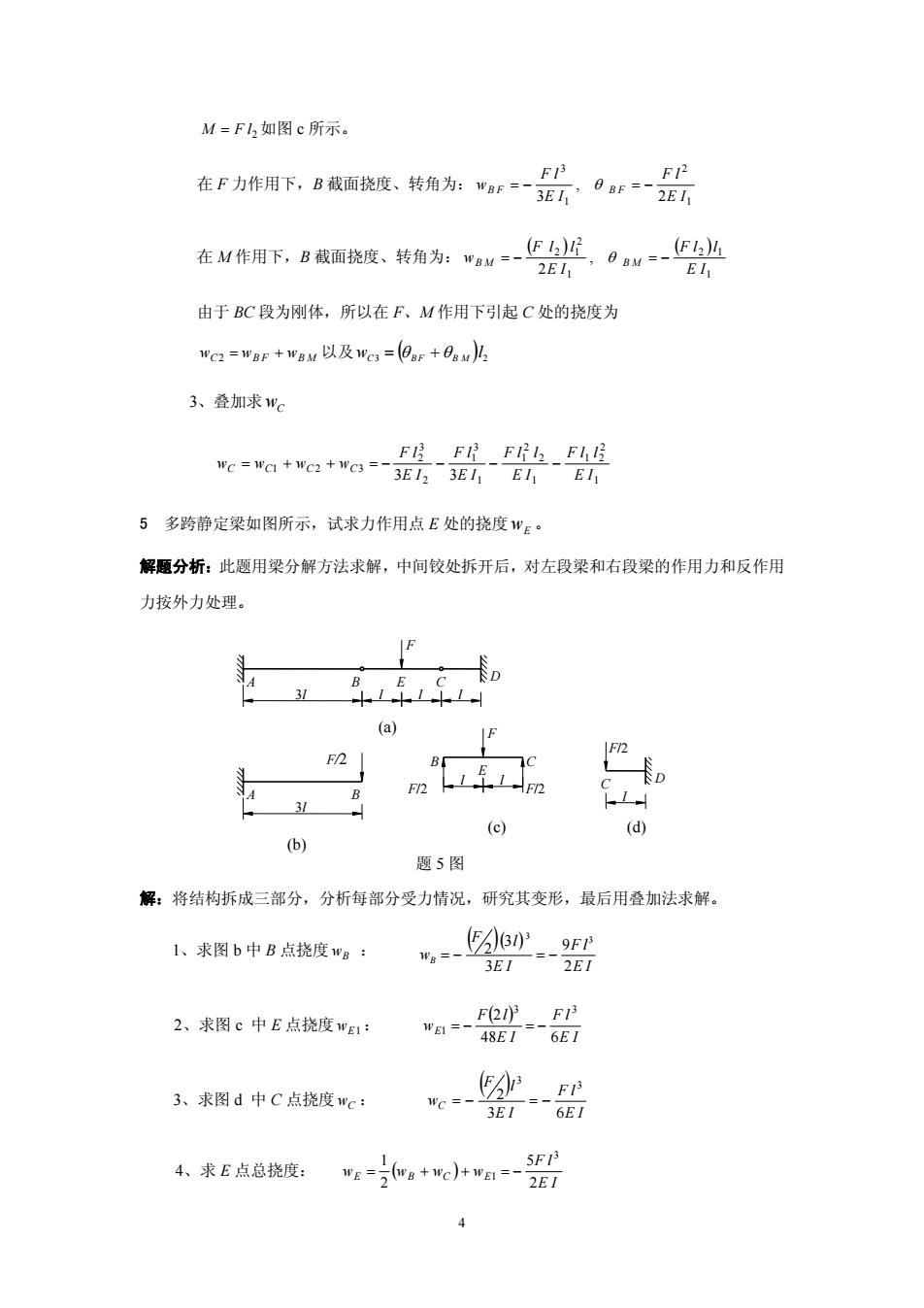
M=F如图c所示。 在F力准用、8我提度、转角为一武。一武 在N作用下,B核面能堂,转角为:w盛9兴 由于BC段为刚体,所以在F、M作用下引起C处的挠度为 wc2=wBr+wau以及we=(但ar+Oawh 3、叠加求wc F月F2_F凸-F4 we-wa+we:+wch EhEh 5多跨静定梁如图所示,试求力作用点E处的挠度wE· 解题分析:此题用梁分解方法求解,中间铰处拆开后,对左段梁和右段梁的作用力和反作用 力按外力处理。 IF F m (b) (c) 题5图 解:将结构拆成三部分,分析每部分受力情况,研究其变形,最后用叠加法求解。 1、求图b中B点挠度wB: 2、求图c中E点挠度wg1: 3、求图d中C点挠度wc: -3E1=-6E7 小求E直每提度一北。+小小a一 4
2 M = F l 如图 c 所示。 在 F 力作用下,B 截面挠度、转角为: 1 2 1 3 2 , 3 E I F l E I F l wB F = − θ B F = − 在 M 作用下,B 截面挠度、转角为: ( ) ( ) 1 2 1 1 2 2 1 , 2 E I F l l E I F l l wB M = − θ B M = − 由于 BC 段为刚体,所以在 F、M 作用下引起 C 处的挠度为 wC2 = wB F + wB M 以及 ( ) 3 2 w l C = θ B F + θ B M 3、叠加求 wC 1 2 1 2 1 2 2 1 1 3 1 2 3 2 1 2 3 3 3 E I F l l E I F l l E I F l E I F l wC = wC + wC + wC = − − − − 5 多跨静定梁如图所示,试求力作用点 E 处的挠度 wE 。 解题分析:此题用梁分解方法求解,中间铰处拆开后,对左段梁和右段梁的作用力和反作用 力按外力处理。 解:将结构拆成三部分,分析每部分受力情况,研究其变形,最后用叠加法求解。 1、求图 b 中 B 点挠度 : wB ( )( ) E I F l E I F l wB 2 9 3 3 2 3 3 = − = − 2、求图 c 中 E 点挠度 : wE1 ( ) E I F l E I F l wE 48 6 2 3 3 1 = − = − 3、求图 d 中 C 点挠度 : wC ( ) E I F l E I F l wC 3 6 2 3 3 = − = − 4、求 E 点总挠度: ( ) E I F l wE wB wC wE 2 5 2 1 3 = + + 1 = − 题 5 图 l C A B 3l B C l (c) F/2 F/2 E l (b) (d) F 3l l l l (a) F/2 F/2 D A B F D E C 4

6图示简支梁AB,在中点处加一弹簧支掉,若使梁的C截面处弯矩为零,试求弹簧常量k, 并绘出梁的剪力图和弯矩图。 期分桥:利用笑C处袋度等于黄第变后,来确定资—中马 常量k F 解:1、求支反力 (a) 设C支座对弹簧的反力为F,A、B处反力分别为 F和F,方向如图所示。根据对称关系,F,= (b) 下a,·在C截面将梁切开,因为C处弯矩为零,则在C af/8 截面左侧有M。=5,-9P=0,所以 (c) 5,=5,=9l. 题6图 由平衡方程∑,=0,即Fy+Fa,+Fc,-2g1=0,得Fe,=91。 2、用叠加法求C点的挠度 a,- 3、确定弹簧常量 梁在C点的挠度就等于弹簧的压缩变形,即 会于提得会-2 4、画剪力、弯矩图:见图b、图c
6 图示简支梁 AB,在中点处加一弹簧支撑,若使梁的 C 截面处弯矩为零,试求弹簧常量 k, 并绘出梁的剪力图和弯矩图。 支座对弹簧的反力为 ,A、B 处反力分别为 和 ,方向如图所示。根据对称关系, = 。在 C 截面将梁切开,因为 C 处弯矩为零,则在 C 截面左侧有 解题分析:利用梁 C 处挠度等于弹簧压缩变形,来确定弹簧 常量 k。 解:1、求支反力 设 C FC y FA y FB y FA y FB y 0 2 1 2 M − = FA yl − ql = C ,所以 F F ql A y B y 2 1 = = 。 由平衡方程 ,即 ,得 2、用叠加法求 C 点的挠度 ∑ = 0 Fy FA y + FB y + FC y − 2q l = 0 F q l C y = 。 ( ) ( ) E I q l E I F l E I C C q C FC y 384 q l w w w C y 48 24 5 2 2 4 3 4 = − = − = 3、确定弹簧常量 梁在 C 点的挠度就等于弹簧的压缩变形,即 k FC y wC = ,于是得 3 wC l F 24E I k C = = 4、画剪力、弯矩图:见图 b、图 c。 (a) q A C B 题 6 图 FAy l l FBy Cy EI F (b) ql2 /8 ql/2 ql/2 ql / ql2 /8 /2 ql 2 (c) 5