弯曲内力 典型习题解析 1作图示简支梁的剪力图和弯矩图,并求出m和Mx· (a) B C F a Fs (e) B F (+) =aa ga 2ga D) M 3a22 B (e) (+) 题1图 解题分析:作剪力、弯矩图的基本方法是写出每一段梁上的剪力、弯矩方程,根据方程描点 作图。在能熟练地作剪力、弯矩图后,可采用如下简便作图法:在表中列出特殊截面(如有 位移约束的截面、集中力作用截面等的剪力、弯矩值,再根据载荷集度与剪力、弯矩之间的 微分关系判断各区段的内力图形状,连线相邻特殊截面对应的点。下面按两种方法分别作图, 解1:1、求支反力 =qa,Fey=2qa 2、将梁分成AB,BC和CD三个区段 以A为原点,向右取x坐标。 AB段,如图d: Fs=F=qa,(0<x<a)
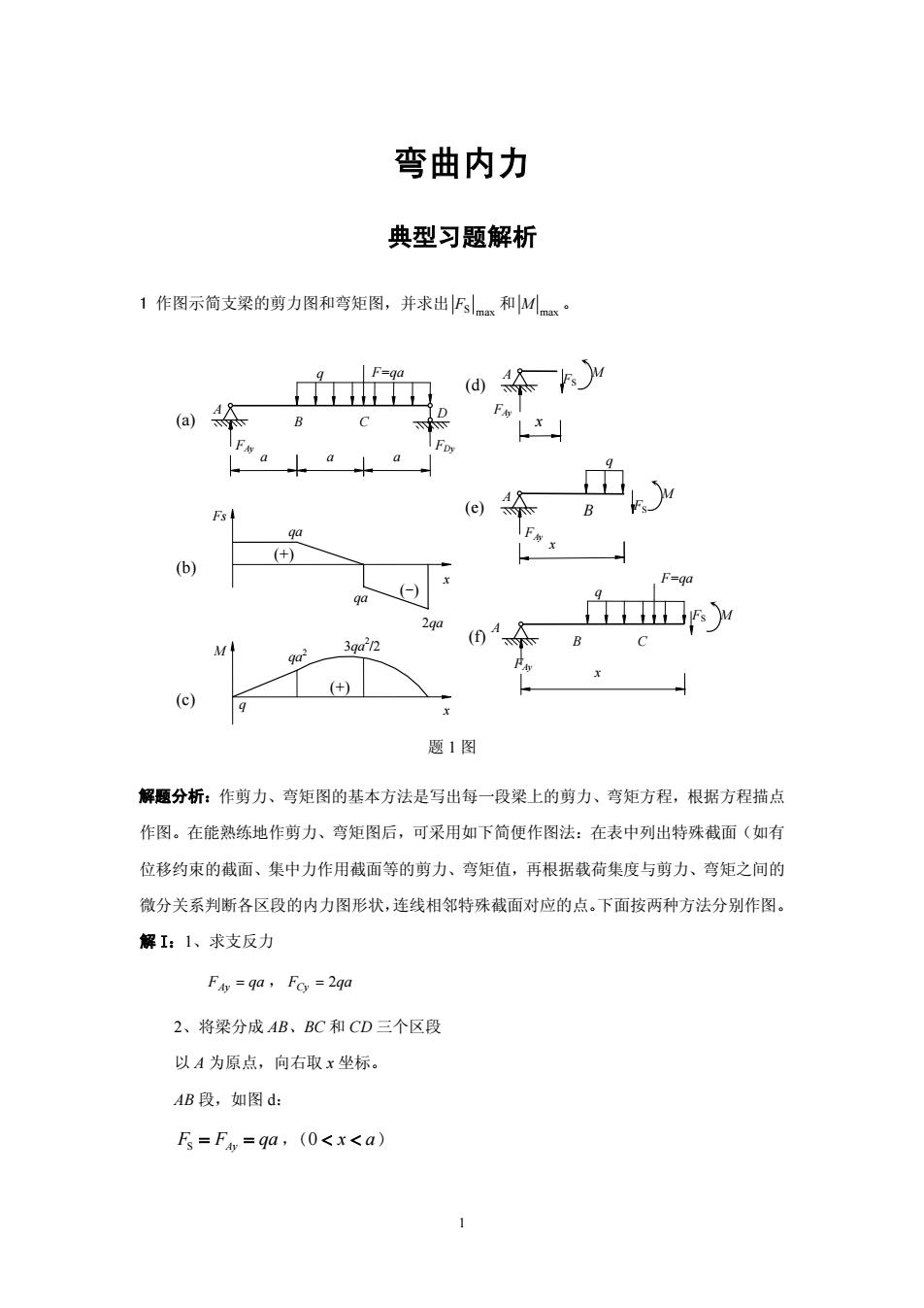
弯曲内力 典型习题解析 1 作图示简支梁的剪力图和弯矩图,并求出 S max F 和 max M 。 解题分析:作剪力、弯矩图的基本方法是写出每一段梁上的剪力、弯矩方程,根据方程描点 作图。在能熟练地作剪力、弯矩图后,可采用如下简便作图法:在表中列出特殊截面(如有 位移约束的截面、集中力作用截面等的剪力、弯矩值,再根据载荷集度与剪力、弯矩之间的 微分关系判断各区段的内力图形状,连线相邻特殊截面对应的点。下面按两种方法分别作图。 解 I:1、求支反力 FAy = qa , FCy = 2qa 2、将梁分成 AB、BC 和 CD 三个区段 以 A 为原点,向右取 x 坐标。 AB 段,如图 d: FS = FAy = qa ,( 0 < x < a ) Fs (+) (-) (+) 2qa qa qa 3qa2 /2 qa2 x x M (c) (b) (a) q FDy D C F=qa A M a B a FAy a A (d) x FAy (e) q B x FAy A M FS FS F=qa q FS M A (f) B C FAy x q 题 1 图 1

M=FAx=qar,(0≤xsa) BC段,如图e: Fs=F-qx(x-a)=q(2a-x),(a<x<2a) M=F4x+q(x-a(x-a)/2=q(x2+ad2)/2,(a≤x≤2a) CD段,如图f: F=F-q×(x-a)-F=g(a-x),(2a<x<3a) M=Fx+q(x-ax-a)/2=q(x2+ar2)/2,(2a≤x≤3a) 3、按照步骤2所得各段梁的剪力、弯矩方程画出剪力图和弯矩图,如图b和图©。 4、计算剪力和弯矩的最大值 IFsl20.a 解Ⅱ:1、计算支反力 Fav=qa,Fcy=2qa 2、将梁分为AB、BC、CD三个区段,计算每个区段起点和终点的力值。 区 AB BC CD 起终点 A Bu C& Fs ga ga 0 -90-2ga M 0 qa' 29a 0 3、根据载荷情况及微分关系,判断各力区的内力图形状,并以相应的图线连接起来 得到剪力图和弯矩图。 力区A截面 AB B截面BCC截面CDD截面 载荷F向上 90 无集中力 g负常数F向下 g负常数F,向上 Fs 突跳F 水平(+)》 连续 下斜线(+)突减F 下斜线(-))突跳F M 0 上斜线相切上凸抛物线转折上凸抛物线0 4、计算剪力弯矩最大值 讨论:利用剪力弯矩方程作图时,注意坐标轴的正向一般由左至右。有时候根据需要,可
M F x qax = Ay = ,( 0 ≤ x ≤ a ) BC 段,如图 e: ( ) (2 ) S F F q x a q a x = Ay − × − = − ,( a < x < 2a ) ( )( )/2 ( )/2 2 2 M F x q x a x a q x a = Ay + − − = + ,( a ≤ x ≤ 2a ) CD 段,如图 f: ( ) ( ) S F F q x a F q a x = Ay − × − − = − ,( 2a < x < 3a ) ( )( )/2 ( )/2 2 2 M F x q x a x a q x a = Ay + − − = + ,( 2a ≤ x ≤ 3a ) 3、按照步骤 2 所得各段梁的剪力、弯矩方程画出剪力图和弯矩图,如图 b 和图 c。 4、计算剪力和弯矩的最大值 F 2qa S max = , 2 max 2 3 M = qa 解 II:1、计算支反力 FAy = qa , FCy = 2qa 2、将梁分为 AB、BC、CD 三个区段,计算每个区段起点和终点的力值。 力区 AB BC CD 起终点 A右 B左 B右 C左 C右 D左 FS qa qa qa 0 - qa -2 qa M 0 2 qa 2 qa 2 2 3 qa 2 2 3 qa 0 3、根据载荷情况及微分关系,判断各力区的内力图形状,并以相应的图线连接起来, 得到剪力图和弯矩图。 力区 A 截面 AB B 截面 BC C 截面 CD D 截面 载荷 FAy向上 q=0 无集中力 q=负常数 F 向下 q=负常数 FDy向上 FS 突跳FAy 水平(+) 连续 下斜线(+) 突减 F 下斜线(-) 突跳FDy M 0 上斜线 相切 上凸抛物线 转折 上凸抛物线 0 4、计算剪力弯矩最大值 F 2qa S max = , 2 max 2 3 M = qa 讨论:利用剪力弯矩方程作图时,注意坐标轴x的正向一般由左至右。有时候根据需要,可 2

以取为由右至左,但此时必须注意q,F和M之间的微分关系在正负号上有变化。 2作图示梁的剪力图和弯矩图。 。4.1。 题2图 解题分析:不分段列剪力、弯矩方程,只计算特殊截面处的剪力、弯矩值,根据规律连线。 解:1、求支反力 Fy=iga.Foy=3qa 2、计算特殊截面剪力值 将梁分为三个区段计算每个截面的F值。集中力作用截面的左、右两侧F值不同。 F佐=0,F佑=90 5a-子q0,56=-9阳 Fc左=-490,Fc=g0 FsD=0 3、计算特殊截面弯矩值 计算前述特殊截面处的M值。集中力偶作用截面的左、右两侧的M值不同。 M4=0 Mt-902,M6=-90
以取为由右至左,但此时必须注意q,FS和M之间的微分关系在正负号上有变化。 2 作图示梁的剪力图和弯矩图。 qa2 q 解题分析:不分段列剪力、弯矩方程,只计算特殊截面处的剪力、弯矩值,根据规律连线。 解:1、求支反力 FAy qa FCy qa 5 4 , 4 3 = = 2、计算特殊截面剪力值 将梁分为三个区段计算每个截面的 FS 值。集中力作用截面的左、右两侧 FS 值不同。 F F qa A A 4 3 0 S 左 = , S 右 = F qa F qa B B 4 1 4 3 S 左 = , S 右 = − F qa F qa SC左 = − , SC右 = 4 1 FSD = 0 3、计算特殊截面弯矩值 计算前述特殊截面处的 M 值。集中力偶作用截面的左、右两侧的 M 值不同。 M A = 0 2 2 4 1 4 3 M qa M qa B左 = , B右 = − (-) qa2 2 4 1 qa 1 2 FS 3 qa 4 4 qa 1 (+) FCy B C a a x (-) qa qa2 (+) 4 3 (+) x FAy M a A D 题 2 图 3
Mc-7qa Mp=0 CD段是二次抛物线,抛物线上有极值时应求出。 4、计算最大剪力和弯矩值 讨论:采用上述作图法不能遗漏代表点,包括载荷变化点、约束点。计算极值弯矩时,可以 先找出该区段剪力为零的截面,该截面处的弯矩即为极值弯矩。也可以借助该区段的弯矩方 程计算极值。 3作图示梁的剪力图和弯矩图,并求出尺l及Mx,B处是中间铰 解题分析:梁上有中间铰时,先自铰处将梁拆分。中 间饺可以传递力,但不能传递弯矩,所以中间较处弯 B 矩一定为零。 al a a 解:1、求支反力 (a) 在中间较B处将梁拆开两部分,较处互相作用 力用F代替,如图b所示。 F-9aFw-fy-7a、M,-7qg 2、将梁分为AB、BC、CD三个区段,计算A、 Fs (b B、C,D截面处的内力值。 3、根据载荷集度与剪力、弯矩之间的微分关系, 判断各区段的内力图形状,并用图线连接。 4、CD段剪力有零点,根据左负右正,判断弯知 图有极小值。 令()=90-=0,得x=a,代入弯 (d) 矩方程 题3客 M=-5n×号a+5导=290 5、计算最大剪力、弯矩值 sLa-子a,Mn-790
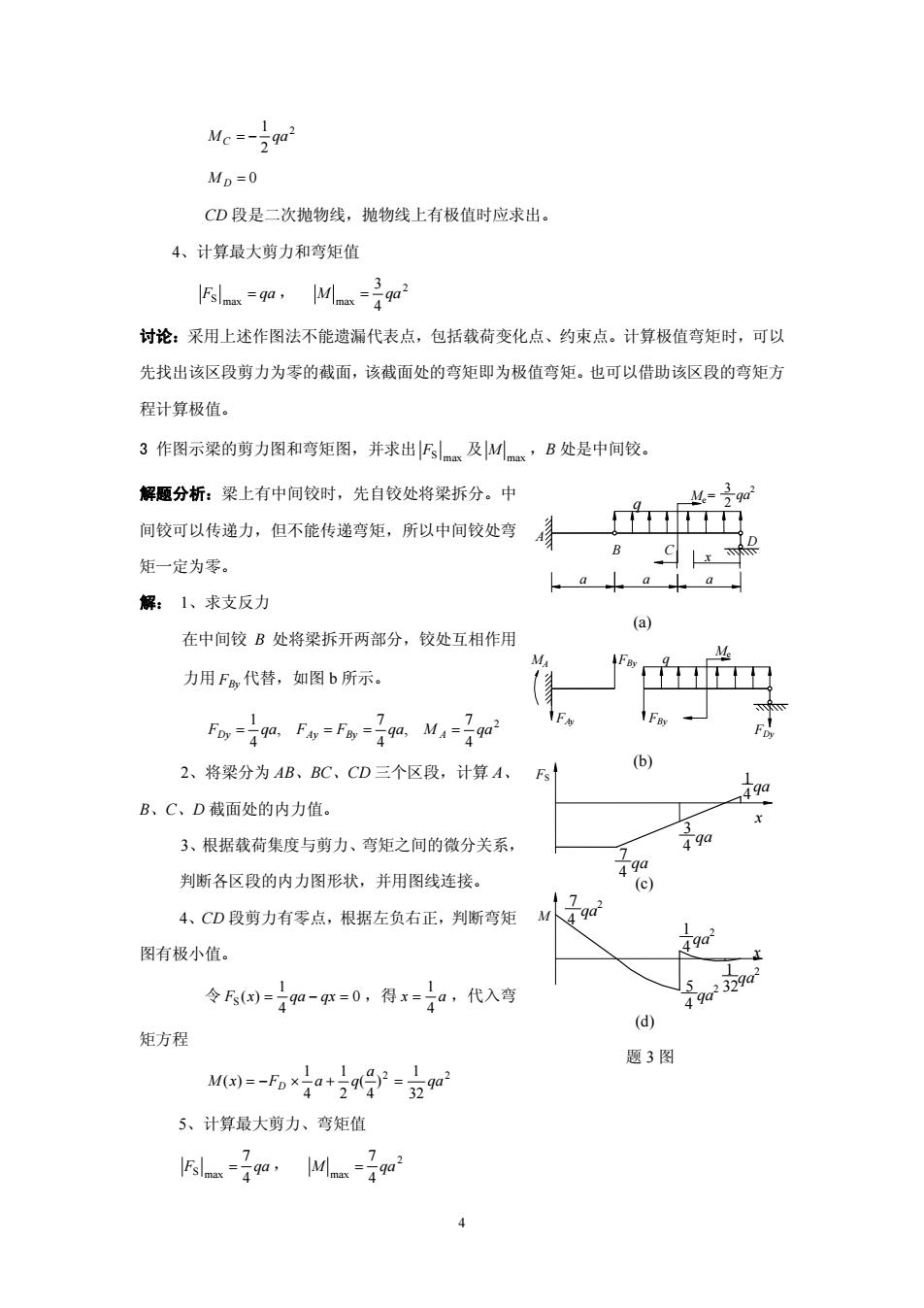
2 2 1 M C = − qa M D = 0 CD 段是二次抛物线,抛物线上有极值时应求出。 4、计算最大剪力和弯矩值 F = qa S max , 2 max 4 3 M = qa 讨论:采用上述作图法不能遗漏代表点,包括载荷变化点、约束点。计算极值弯矩时,可以 先找出该区段剪力为零的截面,该截面处的弯矩即为极值弯矩。也可以借助该区段的弯矩方 程计算极值。 3 作图示梁的剪力图和弯矩图,并求出 S max F 及 max 析:梁上有中间铰时 M ,B 处是中间铰。 解题分 ,先自铰处将梁拆分。中 矩一定为零。 解: 1、求支反力 3 qa2 间铰可以传递力,但不能传递弯矩,所以中间铰处弯 在中间铰 B 处将梁拆开两部分,铰处互相作用 力用 FBy 代替,如图 b 所示。 2 4 7 , 4 7 , 1 F qa FAy = FBy = qa 4 Dy = M A = qa 2、将梁分为 AB、BC、CD 三个区段,计算 A B、C D 截面处的内力值。 3、 集度与剪力、弯矩之间的微分关系, 4、CD 段剪力有零点,根据左负右正,判断弯矩 图有极小值。 、 、 根据载荷 判断各区段的内力图形状,并用图线连接。 令 0 4 1 ( ) S F x = qa − qx = ,得 x a 4 1 = ,代入弯 矩方程 2 2 32 1 ) 4 ( 2 1 4 1 ( ) qa a M x = −FD × a + q = 5、计算最大剪力、弯矩值 F qa 4 S max = , 7 2 max 4 M = 7 qa a a a (a) B C Me= q 2 A D FDy MA F q By Me (b) FAy x FBy 7 4 FS x 4 qa 1 4 (d) 32 qa 5 2 qa 2 1 qa 7 2 M 4 qa 4 1 2 (c) 4 qa x 3 qa 题 3 图 4
4试作图示梁的剪力图和弯矩图 (+) afn2 (+) 题4图 解题分析:对于三角形分布载荷,先列出gx)和的关系,再列出剪力、弯矩方程。结构和 载荷均对称时,弯矩图对称,剪力图反对称。所以,只须取左半边作图,然后根据上述对称 反对称关系,画出另一半剪力、弯矩图 解:1、求支反力 FAy=Fcy=1qol 2、列F、M方程 9)=% 5闭-iw-59r=9o-9号0<x< M4()=9k-95音=婴-x0≤x≤约 x=号处M为极大值。 M=9w3-= 3、作F、M图 AB段,F图为二次抛物线,M图为三次抛物线。 BC段,F图与AB段反对称,M图与AB段对称。 4、计算最大剪力弯矩值
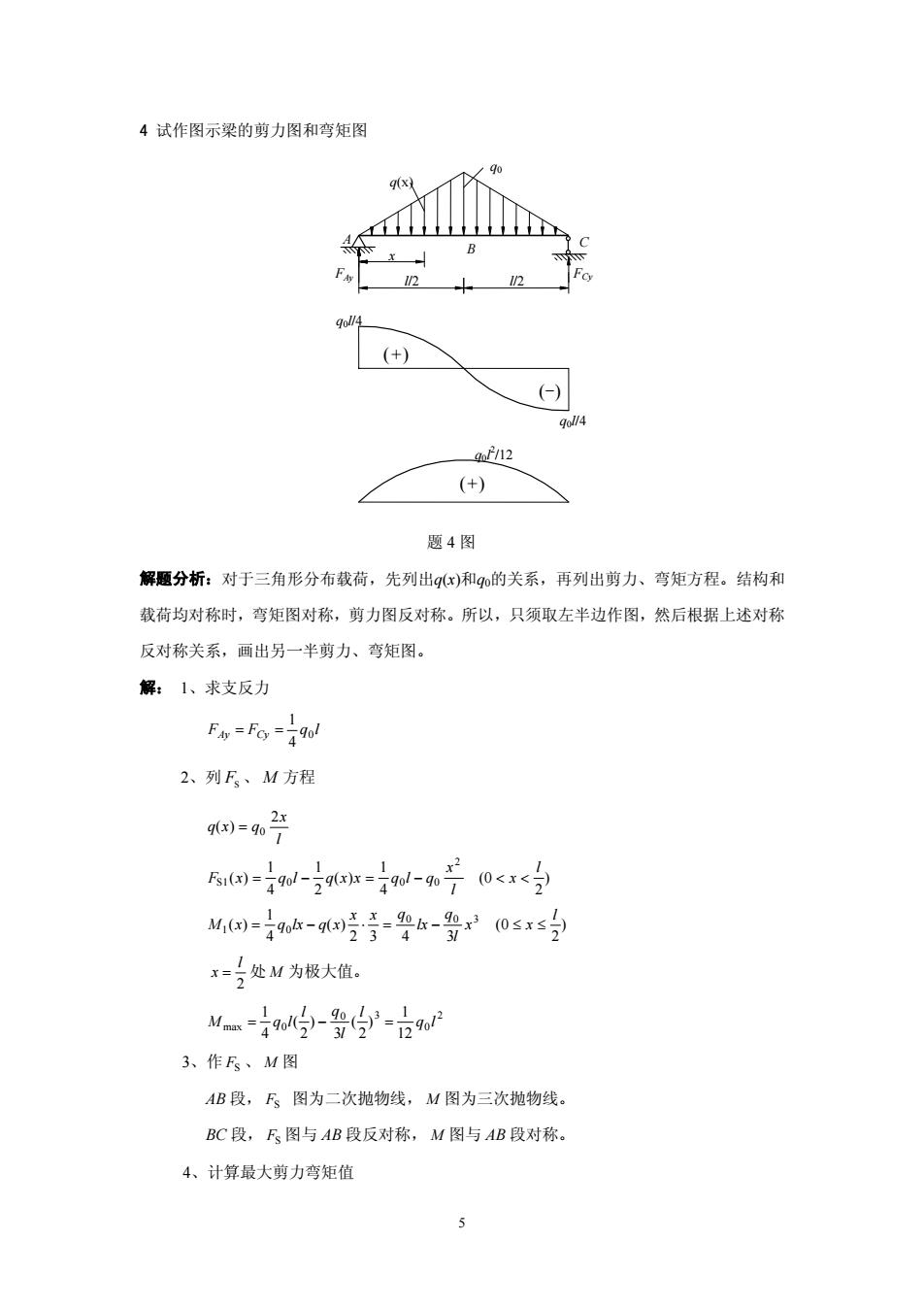
4 试作图示梁的剪力图和弯矩图 解题分析:对于三角形 ( ) q0的关系,再列出剪力、弯矩方程。结构和 载荷均对称时,弯矩图对称,剪力图反对称。所以,只须取左半边作图,然后根据上述对称 解: 1、求支反力 分布载荷,先列出q x 和 反对称关系,画出另一半剪力、弯矩图。 F F q l Ay = Cy = 0 4 1 2、列 FS 、 M 方程 l x q(x = q0 2 ) ) 2 (0 4 1 ( ) 2 1 4 1 ( ) 2 0 0 0 S1 l − l x l x F x = q q x x = q l − q < < ) 2 l (0 2 3 4 3 ( ) 4 1 ( ) 0 0 3 1 0 x x l q lx x x q M x = q lx − q x ⋅ = − ≤ ≤ 2 l x = 处 M 为极大值。 2 0 0 3 ( ) ( ) 1 l q l M max = 0l − 12 1 4 2 3 2 q l l q = 3、作 FS 、 M 图 AB 段, FS 图为二次抛物线, M 图为三次抛物线。 BC 段, FS 图与 AB 段反对称, M 图与 AB 段对称。 4、计算最大剪力弯矩值 q0l/4 l/2 FAy l/2 B x A FCy C q(x) q0 (+) q0l 2 /12 (+) (-) 题 4 q0l/4 图 5

IFslol 5作图示刚架的内力图 Fo 5图 解题分析:刚架有中间较,自铰处拆开,先求支反力,然后根据对称规律作剪力、弯矩图。 铰处无集中载荷时,铰两侧轴力、剪力图连续,弯矩为零。 解:1、求支反力 由于对称F,=F=90 在C纹处拆开,得: Fa-W-Fa 2、作F图 AB力区,FN=-g0,直线: BC,CD区,R=-验,直线: DE力区,F=-g阳,直线。 3、作下图 4B区,9=0,K=-婴直线
4 0 q l = S max F , 1 2 M = q l max 0 12 5 作图示刚架的内力图 C 铰处拆开,得: 解题分析:刚架有中间铰,自铰处拆开,先求支反力,然后根据对称规律作剪力、弯矩图。 铰处无集中载荷时,铰两侧轴力、剪力图连续,弯矩为零。 解:1、求支反力 由于对称 FAy = FEy = qa 在 Ax FEx qa F = = 4 2、作 FN 图 AB 力区, 直线; , 区, FN = −qa , BC CD 力 4 N qa F = − ,直线; 力区, ,直线。 3、 DE FN = −qa 作 FS 图 AB 力区, q = 0 , 4 S qa F = − 直线 C B D qa2 /2 D C D C B B FCx FAx 2a F FEy Ay qa A E FEx B C D a a FAx FAy qa2 /2 A ( ) A 题 5 图 E A /4 qa -) ( (F -) (-) (F qa/4 qa/4 A E M) qa qa 2 /2 B C FCy q ( ( S) N) + qa E qa qa 6

BD力区,g等于负常数,F图为斜线,Fm=g阳 DE力区,q=0,5=婴直线 4、作M图 AB力区,下为负常数,M图为斜线 BC力区,F为斜线,正值,M图为二次抛物线,C处M值等于零。 CD力区,F为斜线,负值,M图为二次抛物线。 DE区,R为正常数。M图为斜线。M-g罗。 讨论:作刚架内力图时充分利用刚架的几何对称性、载荷的对称性或反对称性可以大大降低 工作量
BD 力区, q 等于负常数, FS 图为斜线, F = qa S max DE 力区, q = 0 , 4 S qa F = 直线 4、作 M 图 AB 力区, FS 为负常数, M 图为斜线。 BC 力区, FS 为斜线,正值, M 图为二次抛物线,C 处 M 值等于零。 CD 力区, FS 为斜线,负值, M 图为二次抛物线。 2 2 DE 力区, FS 为正常数, M 图为斜线。 max M = 。 qa 讨论:作 称性或反对称性可以大大降低 工作量。 刚架内力图时充分利用刚架的几何对称性、载荷的对 7