
第三章轴向拉压变形 百嘉火兽
第三章 轴向拉压变形

第三章 轴向拉压变形 §3-1引言 §3-2拉压杆的变形与叠加原理 §3-3桁架的节点位移与小变形的概念 §3-4拉压与剪切应变能 §3-5简单拉压静不定问题 §3-6热应力与初应力
第三章 轴向拉压变形 §3-1 引言 §3-2 拉压杆的变形与叠加原理 §3-3 桁架的节点位移与小变形的概念 §3-4 拉压与剪切应变能 §3-5 简单拉压静不定问题 §3-6 热应力与初应力
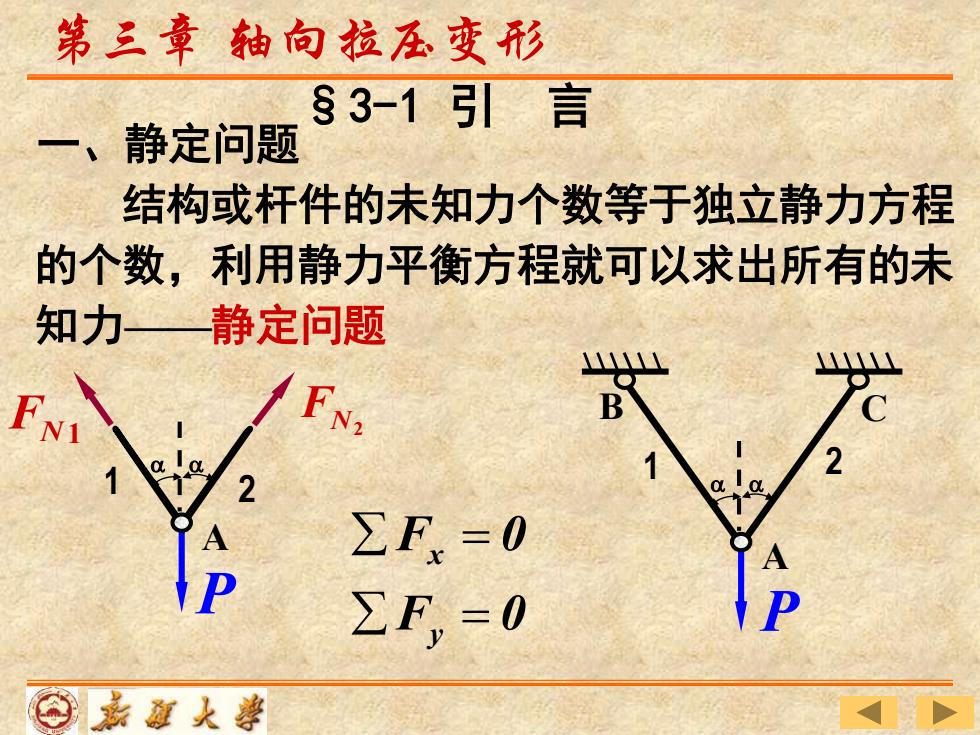
第三章轴向拉压变形 §3-1引言 一、静定问题 结构或杆件的未知力个数等于独立静力方程 的个数,利用静力平衡方程就可以求出所有的未 知力—一静定问题 ∑F.=0 ∑F=0 ⊙嘉火婆
结构或杆件的未知力个数等于独立静力方程 的个数,利用静力平衡方程就可以求出所有的未 知力——静定问题 一、静定问题 x y F 0 F 0 = = 第三章 轴向拉压变形 A B C 1 2 P a a §3-1 引 言 FN 1 N2 F A 1 2 a a P
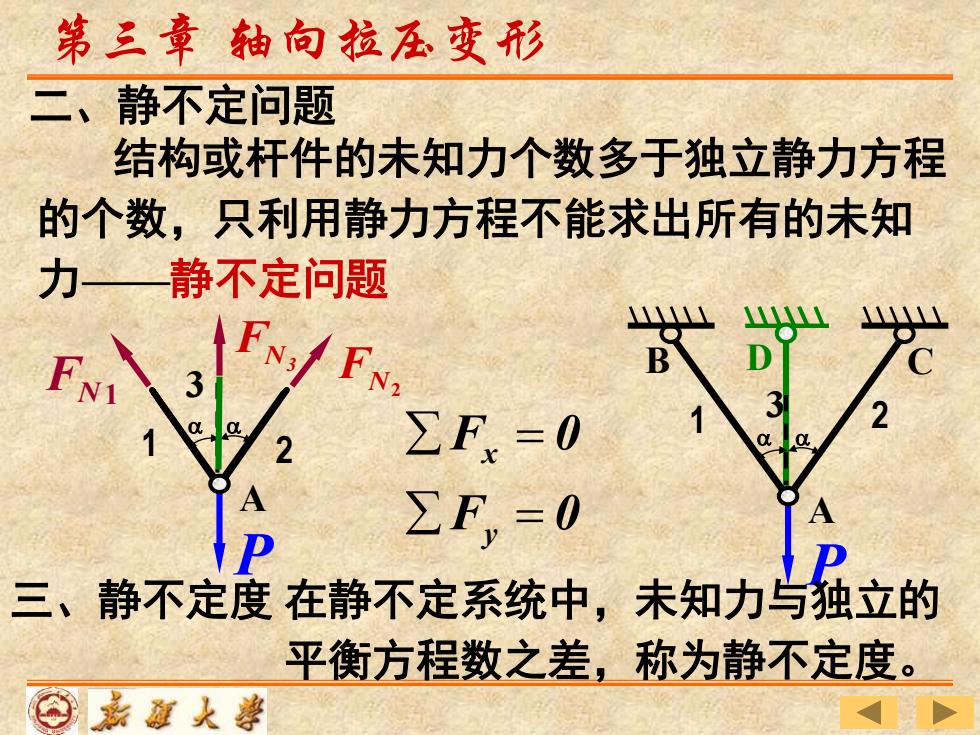
第三章轴向拉压变形 二、静不定问题 结构或杆件的未知力个数多于独立静力方程 的个数,只利用静力方程不能求出所有的未知 力—静不定问题 ∑F.=0 ∑F,=0 三、静不定度在静不定系统中,未知力与独立的 平衡方程数之差,称为静不定度。 ⊙嘉道人導
结构或杆件的未知力个数多于独立静力方程 的个数,只利用静力方程不能求出所有的未知 力——静不定问题 第三章 轴向拉压变形 D 3 二、静不定问题 A B C 1 2 P a a FN 1 N2 F A 1 2 a a P 3 N3 F x y F 0 F 0 = = 三、静不定度 在静不定系统中,未知力与独立的 平衡方程数之差,称为静不定度
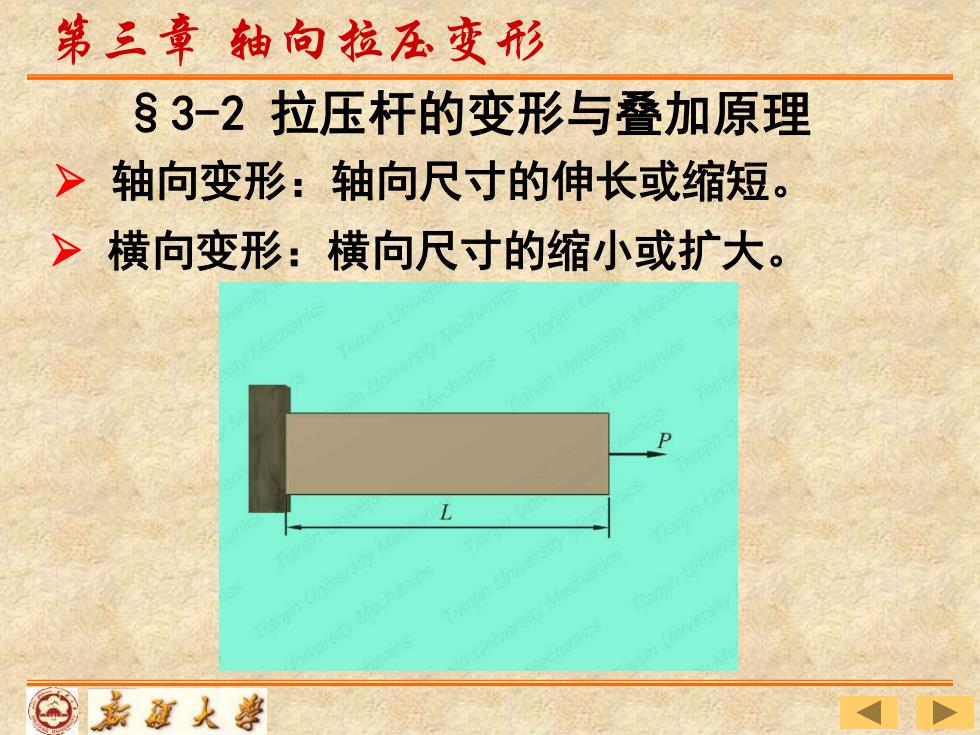
第三章轴向拉压变形 §3-2拉压杆的变形与叠加原理 >轴向变形:轴向尺寸的伸长或缩短。 >横向变形:横向尺寸的缩小或扩大。 ⊙嘉范大事
➢ 轴向变形:轴向尺寸的伸长或缩短。 ➢ 横向变形:横向尺寸的缩小或扩大。 第三章 轴向拉压变形 §3-2 拉压杆的变形与叠加原理

第三章轴向拉在变形 一、拉压杆轴向变形与胡克定律 AL=LI-L, 1.轴向线应变:8= △L L 2.胡克定律: 在线弹性范围内,(当σ≤o,时)8= F △M E A ←L1 △L= FNL k-0- EA (胡克定律的另一种表达方式) ·EA一抗拉(压)刚度 ●△1一伸长为正,缩短为负 嘉面人兽
a1 a L L = 一、拉压杆轴向变形与胡克定律 1.轴向线应变: 2.胡克定律: EA F L L N = (胡克定律的另一种表达方式) L 1 b b E = A FN = l l = ⚫ EA-抗拉(压)刚度 ⚫ l-伸长为正,缩短为负 ΔL= L1 - L , 在线弹性范围内, ( ) 当 p 时 第三章 轴向拉压变形 L1 F F
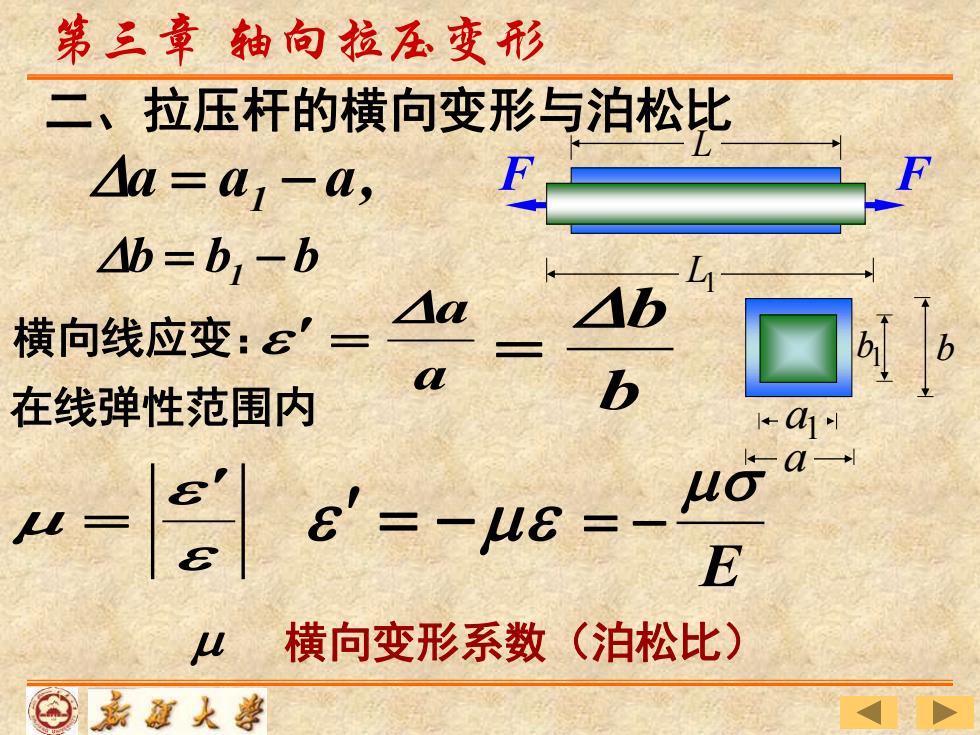
第三章轴向拉压变形 二、拉压杆的横向变形与泊松比 △a=a1-a, F Ab=b1-b 横向线应变:6'= a 在线弹性范围内 1 -|=-e- E u 横向变形系数(泊松比) ⊙嘉题大尊
a1 a b = b1 − b 横向线应变: a a = = 横向变形系数(泊松比) = − a a a, = 1 − b b = 在线弹性范围内 L 1 b b 第三章 轴向拉压变形 E = − L1 F F 二、拉压杆的横向变形与泊松比
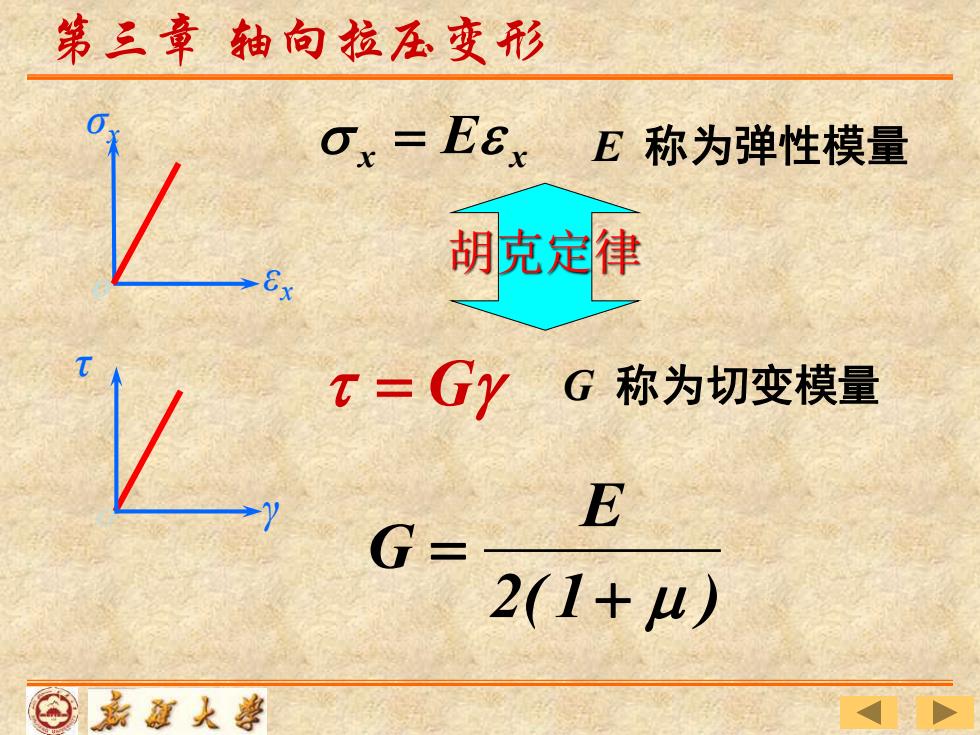
第三章轴向拉压变形 Ox=EExE称为弹性模量 胡克定律 T=GyG称为切变模量 E G= 2(1+4) ⊙嘉道人尊
胡克定律 x E x = = G τ O γ σx ε O x E 称为弹性模量 G 称为切变模量 第三章 轴向拉压变形 2( 1 ) E G + =
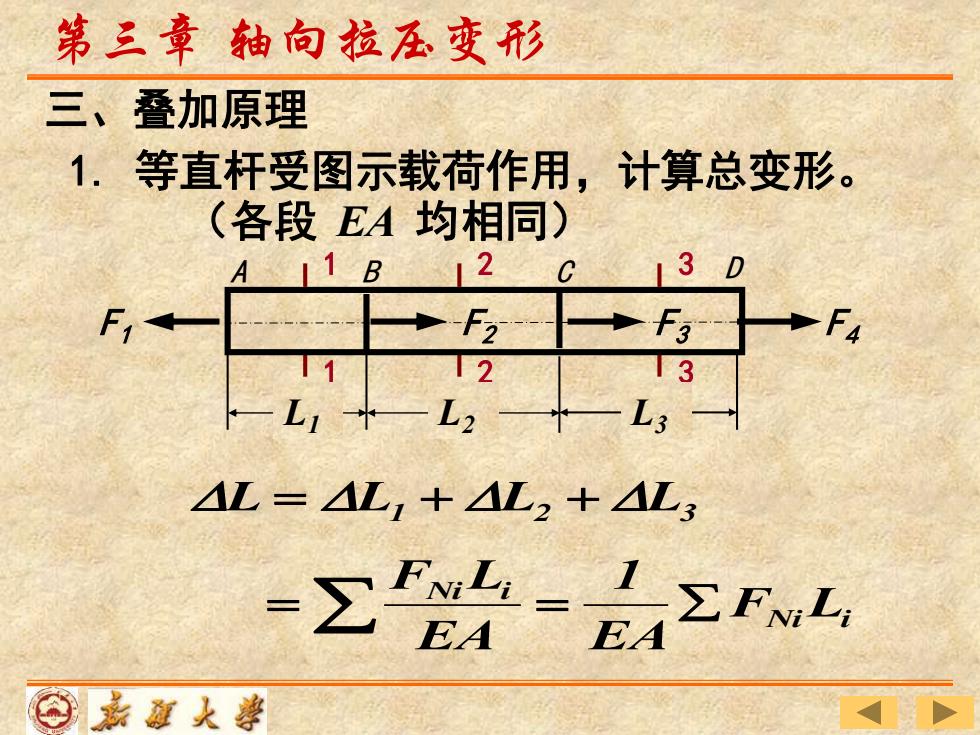
第三章轴向拉压变形 三、叠加原理 1.等直杆受图示载荷作用,计算总变形。 (各段EA均相同) 12 13 D F F3 ◆F4 1 12 13 L L2 L; △L=AL,+AL2+AL3 -∑计=E42rZ EA EA ⊙嘉道大尊
1. 等直杆受图示载荷作用,计算总变形。 (各段 EA 均相同) 三、叠加原理 第三章 轴向拉压变形 L = L1 + L2 + L3 1 1 2 2 3 3 A B C D L1 L2 L3 F1 F2 F3 F4 Ni i Ni i F L EA 1 EA F L = =
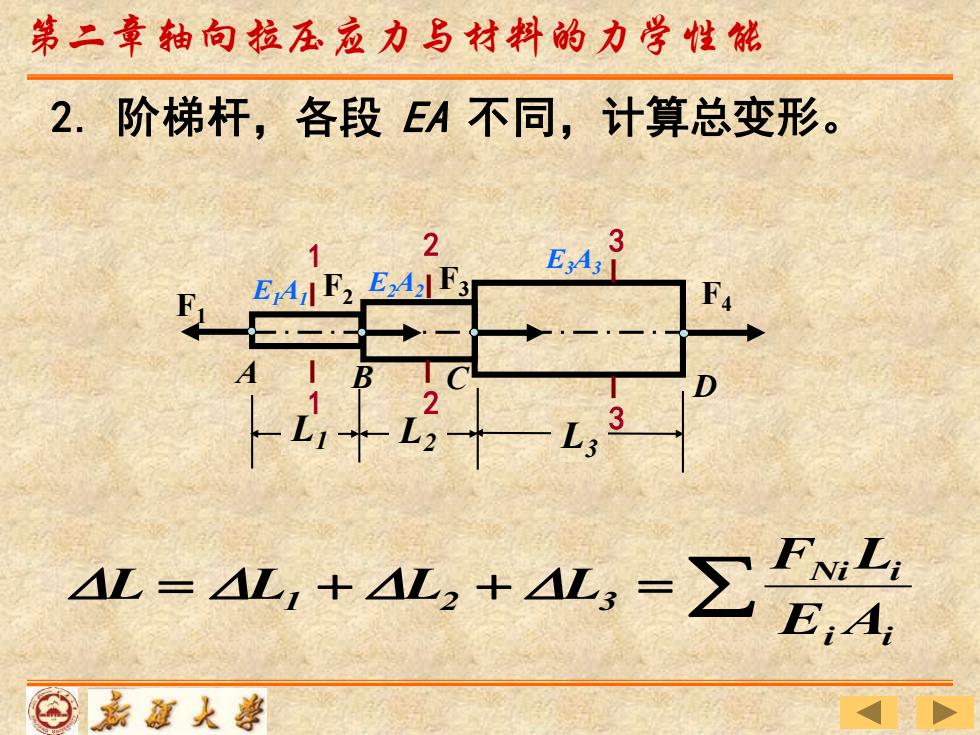
第二章轴向拉在应力与材料的力学性能 2.阶梯杆,各段EA不同,计算总变形。 1 2 3 F2 F3 F 4W=4L,+4,+4L,=∑ EA ⊙嘉道人善
第二章轴向拉压应力与材料的力学性能 A B C D F1 L1 F2 F4 F3 L2 L3 E1A1 E2A2 1 E3A3 1 2 2 3 3 2. 阶梯杆,各段 EA 不同,计算总变形。 L = L1 + L2 + L3 = i i Ni i E A F L