
第三章静定梁与静定刚架 §3-1单跨静定梁计算 一、概述 1、单跨静定梁的结构形式:水平梁、斜梁及曲梁 简支梁、悬臂梁及伸臂梁。分析区别和应用 外力:恒、活、风、雪、地震+反力(和四种约束有关) 2、三个内力分量的规定: 轴力N:拉力+,压力 剪力Q:以绕截面邻近小段隔离体顺时针旋转为十, 反之为一 弯矩M:弯矩使杆件下部受拉时为正,上侧受拉时为 负 3、截面法、分离体、平衡方程:求指定截面的内力的 基本方法。 将指定截面假想截开,切开后截面的内力暴露为外力,取任一局部作为隔离体,作 隔离体受力图(荷载、反力、内力组成平面一般力系或平面汇交力系),由隔离体的 平衡条件可以确定所求截面的三个内力。平面一般力系平衡方程的三种形式。 注意:平衡方程的正负和内力的正负是完全不同性质的两套符号系统。 受力平衡条件:(平面一般力系) 轴力=截面一边的所有外力沿杆轴向投影的代数和(以拉为正): 剪力=截面一边的所有外力沿杆剪切方向的投影代数和(以绕隔离体顺时针为正): 弯矩=截面一边的所有外力对截面形心的力矩代数和(以下拉为正) 画隔离体受力图时,注意: ()隔离体与其周围约束要全部截断,而以相应的约束力代替: (2)约束力要符合约束的性质。截断链杆以轴力代替,截断受弯构件时以轴力、剪力及弯 矩代替,去掉支座时要以相应的支座反力代替。 (3)隔离体是应用平衡条件进行分析的对象。在受力图中只画隔离体本身所受到的力,不 画隔离体施给周围的力: (4)不要遗漏力。包括荷载及截断约束处的约束力: (⑤)未知力一般假设为正号方向,己知力按实际方向画: (6)“三清”:截面左右分清、外力清楚、正负号清楚 4、内力图: 1)定义:表示结构上各截面的内力随横截面位置变化规律的图形。 内力方程式:内力与x(表示横截面位置的变量)之间的函数表达式
第三章 静定梁与静定刚架 §3-1 单跨静定梁计算 一、概述 1、单跨静定梁的结构形式:水平梁、斜梁及曲梁 简支梁、悬臂梁及伸臂梁。分析区别和应用 外力:恒、活、风、雪、地震+反力(和四种约束有关) 2、三个内力分量的规定: 轴力 N:拉力+,压力- 剪力 Q:以绕截面邻近小段隔离体顺时针旋转为+, 反之为- 弯矩 M:弯矩使杆件下部受拉时为正,上侧受拉时为 负 3、截面法、分离体、平衡方程:求指定截面的内力的 基本方法。 将指定截面假想截开,切开后截面的内力暴露为外力,取任一局部作为隔离体,作 隔离体受力图(荷载、反力、内力组成平面一般力系或平面汇交力系),由隔离体的 平衡条件可以确定所求截面的三个内力。平面一般力系平衡方程的三种形式。 注意:平衡方程的正负和内力的正负是完全不同性质的两套符号系统。 受力平衡条件:(平面一般力系) 轴力=截面一边的所有外力沿杆轴向投影的代数和(以拉为正); 剪力=截面一边的所有外力沿杆剪切方向的投影代数和(以绕隔离体顺时针为正); 弯矩=截面一边的所有外力对截面形心的力矩代数和(以下拉为正)。 画隔离体受力图时,注意: (1)隔离体与其周围约束要全部截断,而以相应的约束力代替; (2)约束力要符合约束的性质。截断链杆以轴力代替,截断受弯构件时以轴力、剪力及弯 矩代替,去掉支座时要以相应的支座反力代替。 (3)隔离体是应用平衡条件进行分析的对象。在受力图中只画隔离体本身所受到的力,不 画隔离体施给周围的力; (4)不要遗漏力。包括荷载及截断约束处的约束力; (5)未知力一般假设为正号方向,已知力按实际方向画; (6) “三清”:截面左右分清、外力清楚、正负号清楚 4、 内力图: 1)定义:表示结构上各截面的内力随横截面位置变化规律的图形。 内力方程式:内力与 x(表示横截面位置的变量)之间的函数表达式

2)几点注意 (1)弯矩图画在受拉边、不标明正负,轴力图剪力图画在任一边,标明正负。 (2)内力图名称、单位、控制竖标大小 (3)大小长度按比例、直线要直、曲线光滑 (4)隔离体受力图必须正确,不能漏力多力,己知力(大小方向作用点)、未知力(先 假设为正方向,代入平衡方程,求出正值,说明方向假设正确,求出负值,说明 实际方向和假设相反) (5)平衡方程正负与内力正负是完全不同的两套符号系统。 (6)取简单部分作为隔离体,列平衡方程时,尽量使一个方程含有一个未知量 5、荷载与内力的关系 由平衡条件:∑X=0,N+dN-N+q,d=0 ∑y=0Q+d0-Q+q,.dk=0 ∑M=0 M+0)本+(@+do)5k-(M+dM0=0 推导出: dM is-0 均布荷载作用下: (I)若g.=0,N=const.:若q.=cos1.(均匀),N图为斜直线: (2)若q,=0,Q=const.(水平线):M=斜直线: 若g,=const.,Q=斜直线,M=二次抛物线: =-9,当9,>0时(荷载向下),则M图曲线向下凸。 若为集中荷载作用: ∑X=0,N+dW-N+P=0 ∑Y=0,Q+d№-Q+P,=0 ∑M=0 Q.dx+(Q+dQ)-dx+M+m-(M+dm)=0
2)几点注意 (1)弯矩图画在受拉边、不标明正负,轴力图剪力图画在任一边,标明正负。 (2)内力图名称、单位、控制竖标大小 (3)大小长度按比例、直线要直、曲线光滑 (4)隔离体受力图必须正确,不能漏力多力,已知力(大小方向作用点)、未知力(先 假设为正方向,代入平衡方程,求出正值,说明方向假设正确,求出负值,说明 实际方向和假设相反) (5)平衡方程正负与内力正负是完全不同的两套符号系统。 (6)取简单部分作为隔离体,列平衡方程时,尽量使一个方程含有一个未知量 5、 荷载与内力的关系 由平衡条件: X = 0, N + dN − N + qx .dx = 0 Y = 0 Q + dQ − Q + qy .dx = 0 M = 0 ( ) 0 2 1 ( ) 2 1 M + Q. dx + Q + dQ dx − M + dM = 推导出: qx dx dN = − qy dx dQ = − Q dx dM = 均布荷载作用下: (1)若 qx = 0 ,N=const.;若 q const. x = (均匀),N 图为斜直线; (2)若 qy = 0,Q=const.(水平线); M=斜直线; 若 q const. y = ,Q=斜直线,M=二次抛物线; (3) qy dx d M = − 2 2 当 qy 0 时(荷载向下),则 M 图曲线向下凸。 若为集中荷载作用: X = 0, N + dN − N + Px = 0 Y = 0 ,Q + dQ − Q + Py = 0 M = 0 ( ) 0 2 1 ( ) 2 1 Q. dx + Q + dQ dx + M + m − M + dm =
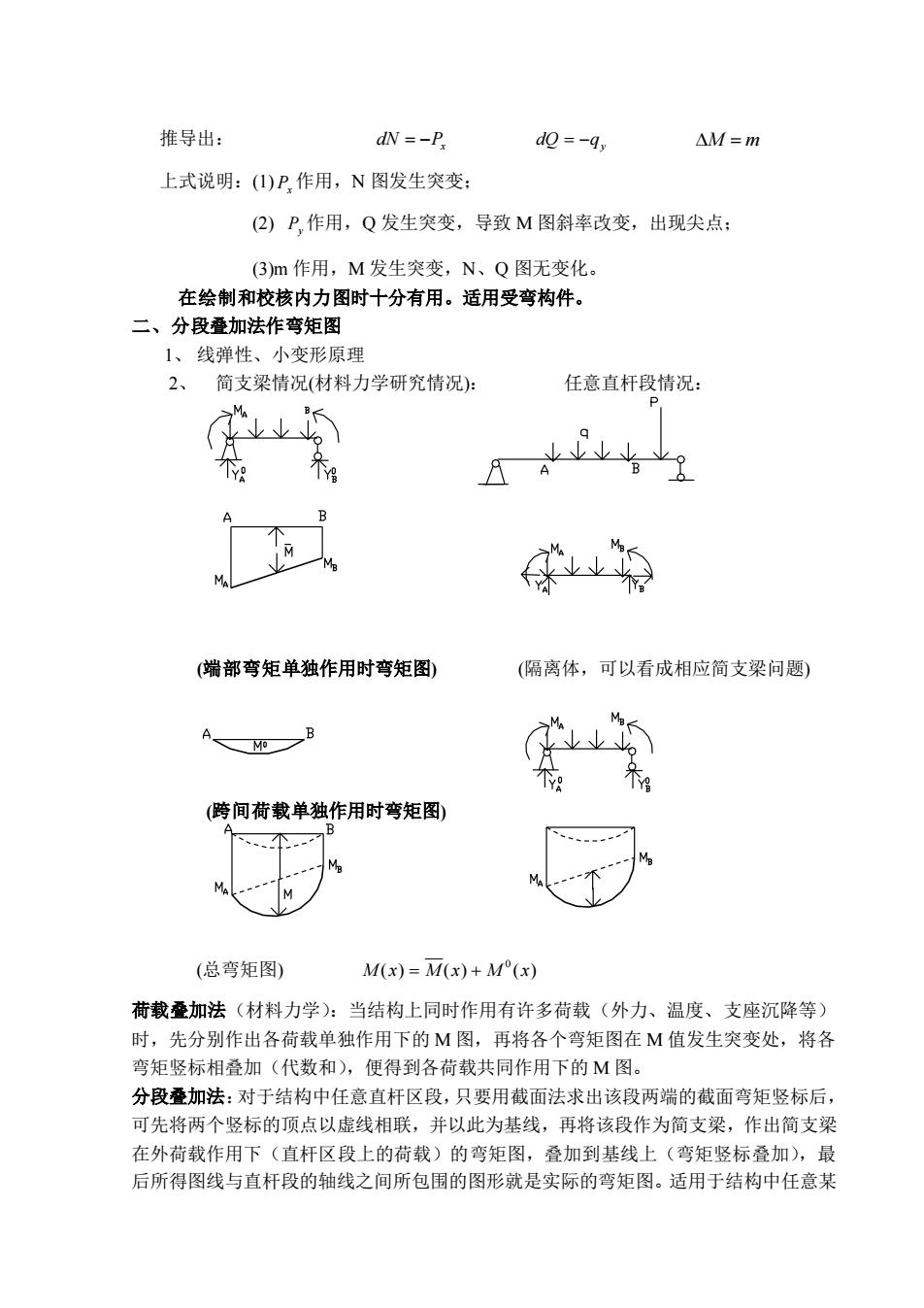
推导出: dN=-P d0=-g, △M=m 上式说明:()P作用,N图发生突变: (2)P作用,Q发生突变,导致M图斜率改变,出现尖点: (3)m作用,M发生突变,N、Q图无变化。 在绘制和校核内力图时十分有用。适用受弯构件。 二、分段叠加法作弯矩图 1、线弹性、小变形原理 2、 简支梁情况(材料力学研究情况): 任意直杆段情况 B M 的 (端部弯矩单独作用时弯矩图) (隔离体,可以看成相应简支梁问题) (跨间荷载单独作用时弯矩图) (总弯矩图) M(x)=M(x)+M(x) 荷载叠加法(材料力学):当结构上同时作用有许多荷载(外力、温度、支座沉降等) 时,先分别作出各荷载单独作用下的M图,再将各个弯矩图在M值发生突变处,将各 弯矩竖标相叠加(代数和),便得到各荷载共同作用下的M图。 分段叠加法:对于结构中任意直杆区段,只要用截面法求出该段两端的截面弯矩竖标后, 可先将两个竖标的顶点以虚线相联,并以此为基线,再将该段作为简支梁,作出简支梁 在外荷载作用下(直杆区段上的荷载)的弯矩图,叠加到基线上(弯矩竖标叠加),最 后所得图线与直杆段的轴线之间所包围的图形就是实际的弯矩图。适用于结构中任意某
推导出: dN = −Px dQ = −qy M = m 上式说明:(1) Px 作用,N 图发生突变; (2) Py 作用,Q 发生突变,导致 M 图斜率改变,出现尖点; (3)m 作用,M 发生突变,N、Q 图无变化。 在绘制和校核内力图时十分有用。适用受弯构件。 二、分段叠加法作弯矩图 1、 线弹性、小变形原理 2、 简支梁情况(材料力学研究情况): 任意直杆段情况: (端部弯矩单独作用时弯矩图) (隔离体,可以看成相应简支梁问题) (跨间荷载单独作用时弯矩图) (总弯矩图) ( ) ( ) ( ) 0 M x = M x + M x 荷载叠加法(材料力学):当结构上同时作用有许多荷载(外力、温度、支座沉降等) 时,先分别作出各荷载单独作用下的 M 图,再将各个弯矩图在 M 值发生突变处,将各 弯矩竖标相叠加(代数和),便得到各荷载共同作用下的 M 图。 分段叠加法:对于结构中任意直杆区段,只要用截面法求出该段两端的截面弯矩竖标后, 可先将两个竖标的顶点以虚线相联,并以此为基线,再将该段作为简支梁,作出简支梁 在外荷载作用下(直杆区段上的荷载)的弯矩图,叠加到基线上(弯矩竖标叠加),最 后所得图线与直杆段的轴线之间所包围的图形就是实际的弯矩图。适用于结构中任意某

直杆区段的弯矩图叠加 弯矩图的叠加,指纵坐标的叠加,而不是指图形的简单拼合。 三、归纳内力图的基本作法 (1)外力(中间连接力对局部研究对象而言是外力):根据结构整体或局部平衡求支座 反力和中间连接力。(避免解联立方程。适当选取隔离体,由平衡方程求解支座和联结 处的约束力) (2)选定外力的不连续点为控制截面(控制截面:如支承点、集中荷载作用点、集中力偶 作用点左右截面、分布荷载的起点及终点等),求控制截面的内力值(采用截面法): (③)分段画弯矩图。采用内力图与荷载的关系。当控制截面间无荷载时,根据控制截面 的弯矩值,即可作出直线弯矩图:当控制截面间有荷载作用时,根据控制截面的弯矩值 作出直线图形后,再叠加上这一段按简支梁求出的弯矩图: (4)分段画剪力图。根据控制截面的剪力竖标,无荷载区段,Q图连以水平线:均匀荷 我区段,O图连以斜直线: (⑤)分段画轴力图。根据控制截面的轴力竖标,在无轴向外荷载区段,N图连以水平线: 在有均匀轴向外荷载区段,N图连以斜直线: (6)校核内力图 (7)N、Q图也可以通过M图由杆件平衡作出。 例1:悬臂梁、简支梁、外伸梁 山山w 444 44 四、斜梁的内力图: 单跨静定斜梁:梁式楼梯、板式楼梯、屋面斜梁,简支斜梁。及具有斜杆的刚架。 两种荷载形式 1、水平向均匀荷载:人群荷载 水平向均匀荷载q,斜角a 1)支座反力:考虑整体平衡 H4=0,'a='B=g12(个) 2)求截面K的内力方程:取AK段隔离体 ∑Mx=0,M=x- (与相应水平简支梁完全一样) 2
直杆区段的弯矩图叠加。 弯矩图的叠加,指纵坐标的叠加,而不是指图形的简单拼合。 三、归纳内力图的基本作法 (1) 外力(中间连接力对局部研究对象而言是外力):根据结构整体或局部平衡求支座 反力和中间连接力。(避免解联立方程。适当选取隔离体,由平衡方程求解支座和联结 处的约束力) (2)选定外力的不连续点为控制截面(控制截面:如支承点、集中荷载作用点、集中力偶 作用点左右截面、分布荷载的起点及终点等),求控制截面的内力值(采用截面法); (3)分段画弯矩图。采用内力图与荷载的关系。当控制截面间无荷载时,根据控制截面 的弯矩值,即可作出直线弯矩图;当控制截面间有荷载作用时,根据控制截面的弯矩值 作出直线图形后,再叠加上这一段按简支梁求出的弯矩图; (4)分段画剪力图。根据控制截面的剪力竖标,无荷载区段,Q 图连以水平线;均匀荷 载区段,Q 图连以斜直线; (5)分段画轴力图。根据控制截面的轴力竖标,在无轴向外荷载区段,N 图连以水平线; 在有均匀轴向外荷载区段,N 图连以斜直线; (6)校核内力图 (7)N、Q 图也可以通过 M 图由杆件平衡作出。 例 1:悬臂梁、简支梁、外伸梁 四、斜梁的内力图: 单跨静定斜梁:梁式楼梯、板式楼梯、屋面斜梁,简支斜梁。及具有斜杆的刚架。 两种荷载形式 1、水平向均匀荷载:人群荷载 水平向均匀荷载 q,斜角α 1) 支座反力:考虑整体平衡 H = 0,V =V = ql / 2() A A B 2) 求截面 K 的内力方程:取 AK 段隔离体 2 2 0, 2 qx x ql M K = M K = − (与相应水平简支梁完全一样)

3、内力图: +glsin a 2 qP/8 -qlsin a2 M图 Q图 N图 注: 1、)横截面: 2、)与等跨简支梁弯矩图相同:(由于竖向支座反力相同,而水平反力均为堆零。) 而N图和Q图有如下关系: N=-Q°sina 0=2°cosa 3、)若将B支座换成:弯矩图、剪力图与上面例题相同, 轴力图不同 3、沿斜向荷载q1:楼梯自重,等效转换根据同一微段上合力相等原则,换算成水平方 向均布荷载:q=ql/cosa 因此内力图为(一)内力图除以cosa +qltg a/2 -gl /2 al/8c qltg a
cos 2 ' 0, ( ) cos = = − = − qx ql Y Q V qx K A 3)、内力图: M 图 Q 图 N 图 注: 1、)横截面: 2、)与等跨简支梁弯矩图相同:(由于竖向支座反力相同,而水平反力均为堆零。) 而 N 图和 Q 图有如下关系: sin 0 N = −Q cos 0 Q = Q 3、)若将 B 支座换成:弯矩图、剪力图与上面例题相同, 轴力图不同 3、沿斜向荷载 q1:楼梯自重,等效转换:根据同一微段上合力相等原则,换算成水平方 向均布荷载:q=q1/cosα 因此内力图为(一)内力图除以 cosα sin 2 ' 0, = = − + qx ql X NK ql2 /8 +qlcosα/2 -qlcosα/2 -qlsinα/2 +qlsinα/2 ql2 /8co sα +ql /2 -ql /2 -qltgα/2 +qltgα/2
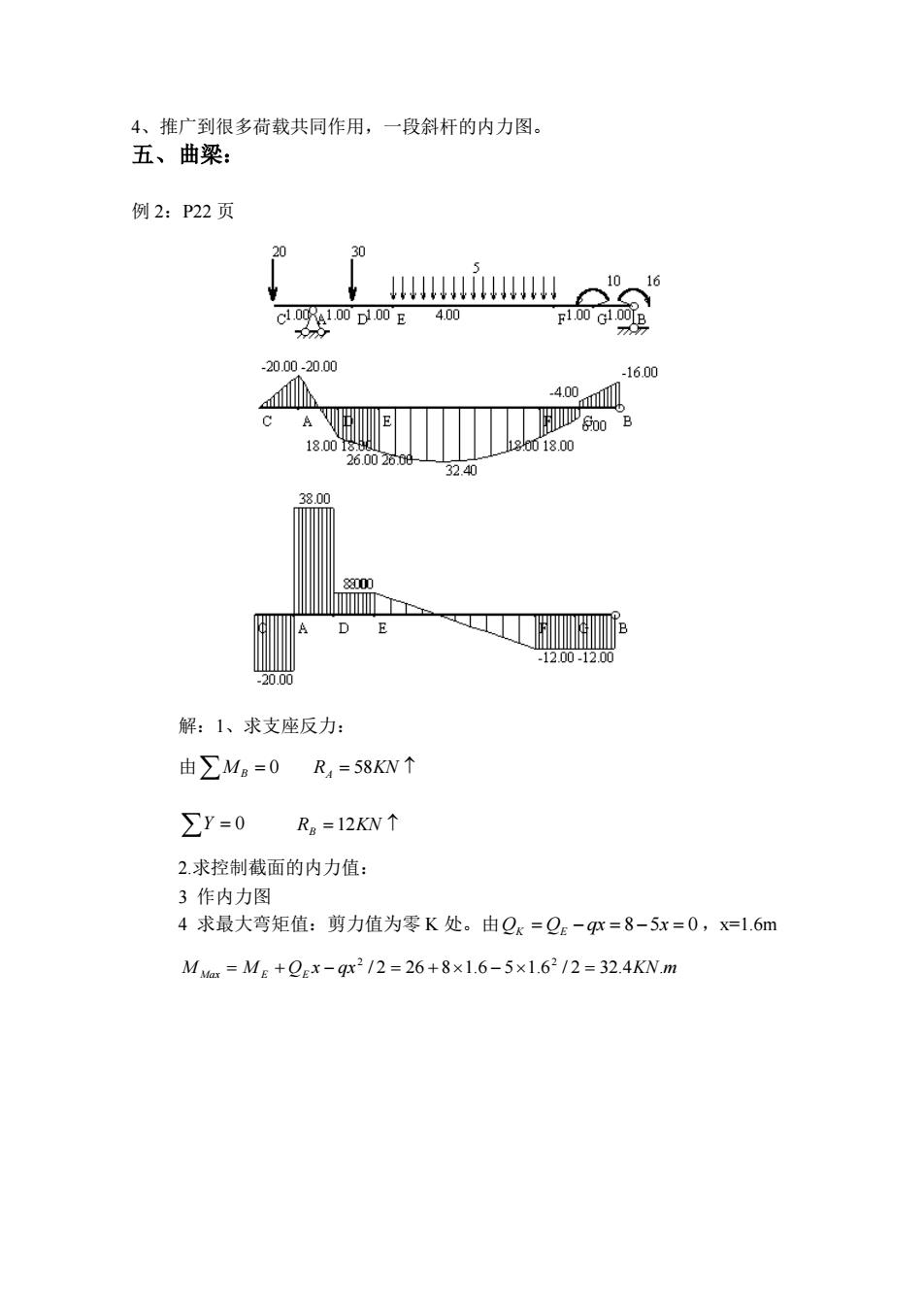
4、推广到很多荷载共同作用,一段斜杆的内力图 五、曲梁: 例2:P22页 30 小 1010 -2000-20.00 6.00 4.00 1800 h0018.00 320 20m -2000 解:1、求支座反力 由∑MB=0R4=58KN个 ∑Y=0RB=12KN↑ 2.求控制截面的内力值: 3作内力图 4求最大弯矩值:剪力值为零K处。由Qx=Qe-体=8-5x=0,X=1.6m Mm=ME+9x-gm2/2-26+8x1.6-5x1.612=32.4KNm
4、推广到很多荷载共同作用,一段斜杆的内力图。 五、曲梁: 例 2:P22 页 解:1、求支座反力: 由 MB = 0 RA = 58KN Y = 0 RB =12KN 2.求控制截面的内力值: 3 作内力图 4 求最大弯矩值:剪力值为零 K 处。由 QK = QE − qx = 8−5x = 0 ,x=1.6m M Max M E QE x qx / 2 26 8 1.6 5 1.6 / 2 32.4KN.m 2 2 = + − = + − =

§3-2多跨静定梁 一、定义: 由若干根梁用铰连接而成、用来跨越几个相连跨度的静定梁。桥梁、房屋建筑中木檩条 连续变形太长导致附加应力和内力,如路面变形缝。 常见的几种形式: (1)无铰跨和两铰跨交替出现: (2)除第一跨外,其余各跨皆有一较 (3)前两种组合方式 n 6,8 二、几何组成特性:若附属部分被切断或撤除,整个基本部分仍为几何不变,反之,若 基本部分被破坏,则其附属部分的几何不变性也连同遭到破坏。 受力特点:基本部分上所受到的荷载对附属部分没有影响,附属部分上作用的外荷载必 然传递到基本部分。 主梁或基本部分:在竖向荷载作用下能独立维持平衡,直接将荷载传到地基 次梁或附属部分:依靠基本部分的支承才可以承受荷载并保持平衡的部分基本部分:多 级附属,相对性 二、多跨静定梁的计算: 原始解法:三个整体静力平衡条件十在较处截面弯矩为零,解联立方程求解。 从几何构造来看,组成的次序是先固定基本部分,后固定附属部分。因此,计算静 定多跨梁时,先计算附属部分,再计算基本部分,将附属部分的支座反力反其指向, 就是加于基本部分的荷载。这样,将多跨梁拆成单跨梁,避免解联立方程。 思路: 1、构造次序:计算次序与构造次序相反: 2、力的传递规律:主梁上外力只传给支座,不传给次梁:但次梁上外力传给主梁 3、计算方法:分层法(对结构进行几何组成分析,分清基本部分和附属部分:先 计算附属部分的反力和内力,再计算基本部分的反力和内力。)将各部分内力图 连成整体,就是多跨梁的内力图。 4、计算关键:基本部分和附属部分之间的相互连接力(作用力和反作用力),求出
§3-2 多跨静定梁 一、定义: 由若干根梁用铰连接而成、用来跨越几个相连跨度的静定梁。桥梁、房屋建筑中木檩条。 连续变形太长导致附加应力和内力,如路面变形缝。 常见的几种形式: (1)无铰跨和两铰跨交替出现: (2)除第一跨外,其余各跨皆有一铰 (3)前两种组合方式 二、几何组成特性:若附属部分被切断或撤除,整个基本部分仍为几何不变,反之,若 基本部分被破坏,则其附属部分的几何不变性也连同遭到破坏。 受力特点:基本部分上所受到的荷载对附属部分没有影响,附属部分上作用的外荷载必 然传递到基本部分。 主梁或基本部分:在竖向荷载作用下能独立维持平衡,直接将荷载传到地基。 次梁或附属部分:依靠基本部分的支承才可以承受荷载并保持平衡的部分基本部分:多 级附属,相对性 二、多跨静定梁的计算: 原始解法:三个整体静力平衡条件+在铰处截面弯矩为零,解联立方程求解。 从几何构造来看,组成的次序是先固定基本部分,后固定附属部分。因此,计算静 定多跨梁时,先计算附属部分,再计算基本部分,将附属部分的支座反力反其指向, 就是加于基本部分的荷载。这样,将多跨梁拆成单跨梁,避免解联立方程。 思路: 1、构造次序:计算次序与构造次序相反; 2、 力的传递规律:主梁上外力只传给支座,不传给次梁;但次梁上外力传给主梁; 3、 计算方法:分层法(对结构进行几何组成分析,分清基本部分和附属部分;先 计算附属部分的反力和内力,再计算基本部分的反力和内力。)将各部分内力图 连成整体,就是多跨梁的内力图。 4、 计算关键:基本部分和附属部分之间的相互连接力(作用力和反作用力),求出

这些连接力后,各部分当作单跨静定梁来计算。分段作内力图。拼接 分析步豫: 1、几何组成分析:分清主次部分 2、分层:将附属部分的支座反力反向指其基本部分,就是加于基本部分的荷载: 3、内力图:各单跨梁的内力图连在一起 例1: 10 4404444 A200B400 4.00 2。 H=0 400 V=5KN 4.0可 2 解:1.画层次图 2.逐段做内力图3.拼合内力图
这些连接力后,各部分当作单跨静定梁来计算。分段作内力图。拼接 分析步骤: 1、几何组成分析:分清主次部分 2、分层:将附属部分的支座反力反向指其基本部分,就是加于基本部分的荷载; 3、内力图:各单跨梁的内力图连在一起 例 1: 解:1.画层次图 2.逐段做内力图 3.拼合内力图 VB=5KN VC=5KN HB=0 HC=0 5KN RD=7.5KN RE=21.5KN 5KN VA=9KN MA=18KN.m
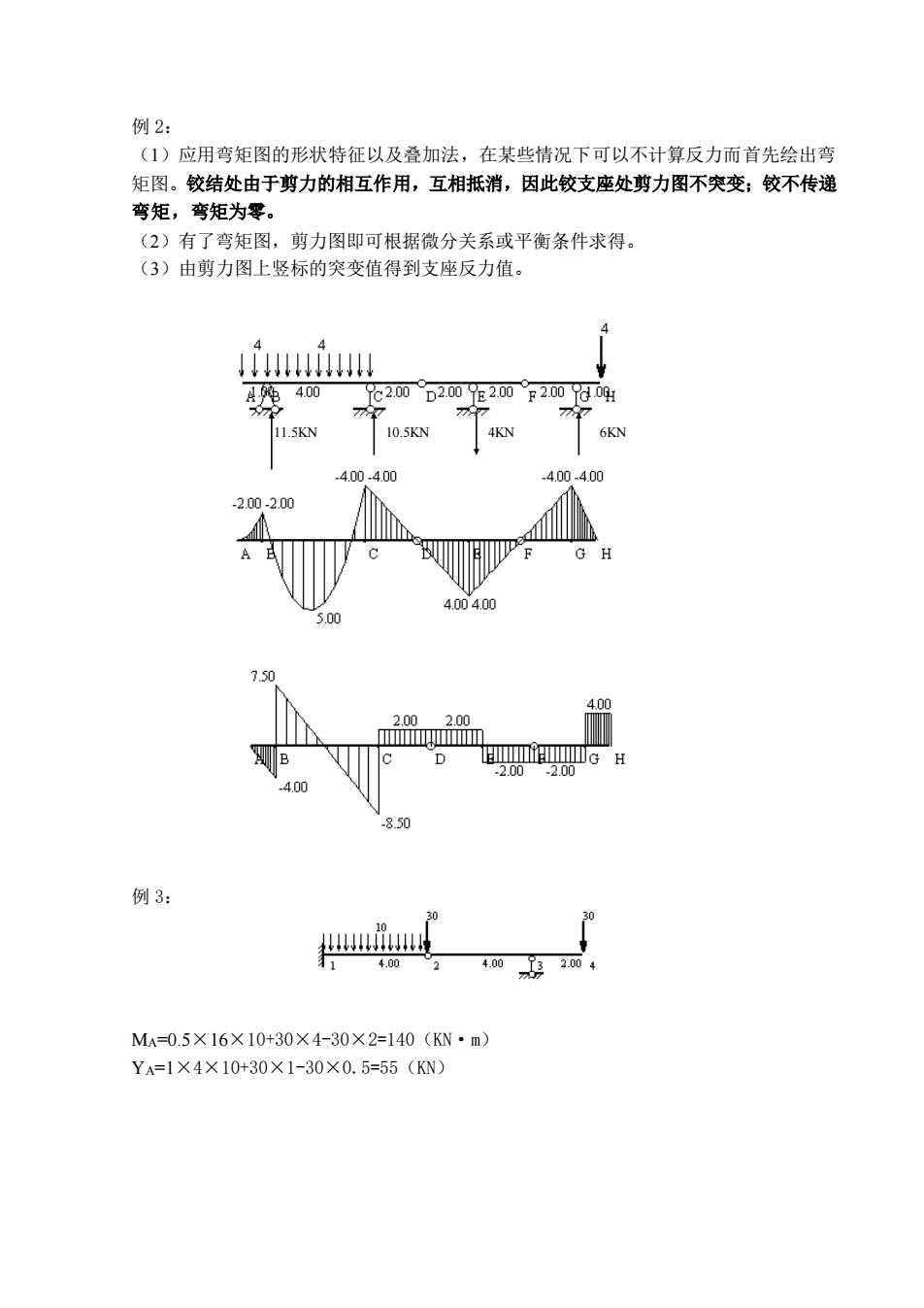
例2: (1)应用弯矩图的形状特征以及叠加法,在某些情况下可以不计算反力而首先绘出弯 矩图。铰结处由于剪力的相互作用,互相抵消,因此铰支座处剪力图不突变;铰不传递 弯矩,弯矩为零。 (2)有了弯矩图,剪力图即可根据微分关系或平衡条件求得。 (3)由剪力图上竖标的突变值得到支座反力值。 14u 4 40m 200D2007E200F200804 5KN D 850 例3: MA=-0.5×16×10+30×4-30×2=140(KN·m) YA=1×4×10+30×1-30×0.5=55(KN)
例 2: (1)应用弯矩图的形状特征以及叠加法,在某些情况下可以不计算反力而首先绘出弯 矩图。铰结处由于剪力的相互作用,互相抵消,因此铰支座处剪力图不突变;铰不传递 弯矩,弯矩为零。 (2)有了弯矩图,剪力图即可根据微分关系或平衡条件求得。 (3)由剪力图上竖标的突变值得到支座反力值。 例 3: MA=0.5×16×10+30×4-30×2=140(KN·m) YA=1×4×10+30×1-30×0.5=55(KN) 11.5KN 10.5KN 4KN 6KN

§3-3静定平面刚架 一.刚架的应用和形式 平面杆件结构:梁、刚架、桁架、拱、组合结构 混合结构、钢筋混凝土结构、钢结构、木结构、新型材料结构 钢筋混凝土结构:框架、框架剪力墙、全剪力墙、筒体、巨型框架 结构是在发展的:梁(混合结构)的缺点(应力沿杆轴线方向不均匀,自重大)薄腹梁、 变截面梁:发展到钢筋混凝土刚架 刚架的形式: 静定(单跨+多跨)+超静定(单跨+多跨)在建筑工程中应用十分广泛,单层厂房、工 业和民用建筑如主楼、教学楼、图书馆。6~15层房屋建筑承重结构体系主要是刚架: 悬臂刚架(小报栏入、三铰刚架、两铰、简支、无铰、多层多跨、封闭刚架、多跨静定; 绘图表示。其中大多数刚架是超静定结构,但静定刚架是超静定刚架计算的基础。 平面刚架的定义:由轴线在同一平面内的若干梁柱主要用刚结点组成的结构 静定刚架常见形式举例: 悬臂刚架、简支刚架、三铰刚架、组合刚架 二.刚架的特征(结合图进行说明) 1)变形:刚结点处,各杆端不能产生相对移动和转动,各杆所夹角度不变。 2)受力:刚结点能够承受和传递弯矩,使结构弯矩分布相对比较均匀,节省材料 3)几何组成:两较三铰刚架和四铰体系变为结构加斜杆比较,组成几何不变体系所需 的杆件数目较少,且多为直杆,故净空较大,施工方便。 4)刚架的优点:梁柱形成一个刚性整体,增大了结构刚度并使内力分布比较均匀,节 省材料,可以获得较大的净空。 三.刚架的内力计算
§3-3 静定平面刚架 一.刚架的应用和形式 平面杆件结构:梁、刚架、桁架、拱、组合结构 混合结构、钢筋混凝土结构、钢结构、木结构、新型材料结构 钢筋混凝土结构:框架、框架剪力墙、全剪力墙、筒体、巨型框架 结构是在发展的:梁(混合结构)的缺点(应力沿杆轴线方向不均匀,自重大)薄腹梁、 变截面梁:发展到钢筋混凝土刚架 刚架的形式: 静定(单跨+多跨)+超静定(单跨+多跨)在建筑工程中应用十分广泛,单层厂房、工 业和民用建筑如主楼、教学楼、图书馆。6~15 层房屋建筑承重结构体系主要是刚架: 悬臂刚架(小报栏)、三铰刚架、两铰、简支、无铰、多层多跨、封闭刚架、多跨静定, 绘图表示。其中大多数刚架是超静定结构,但静定刚架是超静定刚架计算的基础。 平面刚架的定义:由轴线在同一平面内的若干梁柱主要用刚结点组成的结构。 静定刚架常见形式举例: 悬臂刚架、简支刚架、三铰刚架、组合刚架 二.刚架的特征(结合图进行说明) 1)变形:刚结点处,各杆端不能产生相对移动和转动,各杆所夹角度不变。 2)受力:刚结点能够承受和传递弯矩,使结构弯矩分布相对比较均匀,节省材料。 3)几何组成:两铰三铰刚架和四铰体系变为结构加斜杆比较,组成几何不变体系所需 的杆件数目较少,且多为直杆,故净空较大,施工方便。 4)刚架的优点:梁柱形成一个刚性整体,增大了结构刚度并使内力分布比较均匀,节 省材料,可以获得较大的净空。 三. 刚架的内力计算