
第九章渐进法 §9-1概述 现代工程结构中出现了越来越多的超静定结构,其中大多数是梁和刚架(组合结构), 如:教学楼,图书馆、外招、科学馆、电教馆等。 基本解法:力法,位移法但是我们发现:无论是力法或位移法,如果未知量数目在 三个以内,算起来比较容易,三个一五个,有点费劲,五个以上一十个,比较困难,而 十个以至更多未知量,很困难或无法用力法或位移法计算,而工程实际结构,也就是横 向三跨七层刚架4×7+7=35个(位移法)7×3×3=63个(力法)。纵向连续梁,七跨或 八跨,也有7、8个未知量。 用力法及位移法求解十分困难,逼的人们又想其它方法,于是近几十年来,在力法 几位移法的基础上,又发展了许多实用的计算方法:(渐进法,数值法)。 「力矩分配法:适用于无结点线位移的刚架AD多跨连续梁 力矩分配法和位移法联合应用:有侧移刚架(线位移较多时,也很麻烦)主要用在单 层多跨刚架 无剪力分配法:一些特殊的有侧移刚架。 迭代法:多层多跨刚架 力矩分配法和位移法联合求解:单层多跨刚架,有侧移 电算:(矩阵位移法OR有限元法) 手算:1、精确力法、位移法、混合法缺点:当未知量较多时 2、渐进法力矩分配法、无剪力分配法、迭代法、反弯点(D值法入、弯矩二次 分配法、联合法优点:避免求解联立方程组,但又能满足工程需要 电算:矩阵力法、矩阵位移法、矩阵混合法 力矩分配法: 无剪力分配法:单层多跨对称刚架(工业厂房)和一些特殊的有侧移刚架 和力矩分配法类似的渐进法 迭代法:多层刚架(多个线位移),有、无侧移刚架均可。(有较接点,简式刚架, 复式刚架和变截面杆件组成的刚架。) 这两种方法的理论基础均是位移法,在计算中采用逐次修正的步骤,一轮一轮的提 高计算精度。机械→简单。 其他对于多层多跨刚架近似方法: 分层法:多层多跨刚架在竖向荷载作用下: 反弯点法:水平荷载,层数不多的多层多跨刚架: D值法:水平荷载作用下层数较多的高层多跨刚架: 弯矩二次分配法:竖向荷载作用下多层多跨刚架:
第九章 渐进法 §9-1 概述 现代工程结构中出现了越来越多的超静定结构,其中大多数是梁和刚架(组合结构), 如:教学楼,图书馆、外招、科学馆、电教馆等。 基本解法:力法,位移法但是我们发现:无论是力法或位移法,如果未知量数目在 三个以内,算起来比较容易,三个—五个,有点费劲,五个以上—十个,比较困难,而 十个以至更多未知量,很困难或无法用力法或位移法计算,而工程实际结构,也就是横 向三跨七层刚架 4×7+7=35 个(位移法)7×3×3=63 个(力法)。纵向连续梁,七跨或 八跨,也有 7、8 个未知量。 用力法及位移法求解十分困难,逼的人们又想其它方法,于是近几十年来,在力法 几位移法的基础上,又发展了许多实用的计算方法:(渐进法,数值法)。 力矩分配法:适用于无结点线位移的刚架 AND 多跨连续梁 力矩分配法和位移法联合应用:有侧移刚架(线位移较多时,也很麻烦)主要用在单 层多跨刚架 无剪力分配法:一些特殊的有侧移刚架。 迭代法:多层多跨刚架 力矩分配法和位移法联合求解:单层多跨刚架,有侧移 电算:(矩阵位移法 OR 有限元法) 手算:1、精确 力法、位移法、混合法 缺点:当未知量较多时 2、渐进法 力矩分配法、无剪力分配法、迭代法、反弯点(D 值法)、弯矩二次 分配法、联合法 优点:避免求解联立方程组,但又能满足工程需要 电算:矩阵力法、矩阵位移法、矩阵混合法 力矩分配法:; 无剪力分配法:单层多跨对称刚架(工业厂房)和一些特殊的有侧移刚架 和力矩分配法类似的渐进法 迭代法:多层刚架(多个线位移),有、无侧移刚架均可。(有铰接点,简式刚架, 复式刚架和变截面杆件组成的刚架。) 这两种方法的理论基础均是位移法,在计算中采用逐次修正的步骤,一轮一轮的提 高计算精度。机械→简单。 其他对于多层多跨刚架近似方法: 分层法:多层多跨刚架在竖向荷载作用下; 反弯点法:水平荷载,层数不多的多层多跨刚架; D 值法:水平荷载作用下层数较多的高层多跨刚架; 弯矩二次分配法:竖向荷载作用下多层多跨刚架;

§9-2转动刚度、传递系数 理论基础是位移法,解题方法是渐进法。 杆端M的正负和位移法相同。 1、转动刚度(劲度系数)S:不同杆件对于杆端转动的抵抗能力是不同的。杆件AB的 A端(或称近端)产生单位转角时,A端所需施加的力矩值 与杆件线刚度1及远端支承条件有关: 远端为固定支座:S=41 铰支座:S=3i 定向支座:S=i 自由端:Sa=0 注:将A端看成可转动不可移动的刚结点,SB就代表当刚结点产生单位转角时杆端A 引起的杆端弯矩。 2、传递系数C:当杆件AB仅在A端有转角时,引起B端的弯矩MA称为传递弯矩。 C=MB 远端为固定支座:CB=1/2 铰支座、自由端:C=0 定向支座:CB=-1 MR=CARM 3、弯矩分配系数:只有一个结点角位移,且在相应结点作用作用一个外力偶的超静定 结构 基本未知量Z 转角位移方程: 位移祛基本方程: 求Z各杆端弯矩:近端e、远端f =→M图 MAB =3iAB.Z SAR Z Mac =isc.Z=Sac.Z MAD 4iAD Z =SAD.Z 根据平衡条件: MAB十MAC十MAD=M %, M=S人 Mo=S人 S,M Me-Ss M 注:I、M将汇交于A结点各杆的转动刚度的比例分配给各杆的A端,转动刚度越大, 所承担的弯矩越大
§9-2 转动刚度、传递系数 理论基础是位移法,解题方法是渐进法。 杆端 M 的正负和位移法相同。 1、转动刚度(劲度系数)S:不同杆件对于杆端转动的抵抗能力是不同的。杆件 AB 的 A 端(或称近端)产生单位转角时,A 端所需施加的力矩值 与杆件线刚度 I 及远端支承条件有关: 远端为固定支座: S i AB = 4 铰支座: S i AB = 3 定向支座: S i AB = 自由端: SAB = 0 注:将 A 端看成可转动不可移动的刚结点,SAB就代表当刚结点产生单位转角时杆端 A 引起的杆端弯矩。 2、传递系数 C:当杆件 AB 仅在 A 端有转角时,引起 B 端的弯矩 MBA 称为传递弯矩。 AB BA AB M M C = 远端为固定支座: CAB =1/ 2 铰支座、自由端: CAB = 0 定向支座: CAB = −1 MBA CAB MAB = . 3、弯矩分配系数 u:只有一个结点角位移,且在相应结点作用作用一个外力偶的超静定 结构 (E) 基本未知量 Z1 转角位移方程: 位移法基本方程: 求 Z1各杆端弯矩:近端 e、远端 f M 图 1 1 MAB = 3iAB.Z = SAB.Z 1 1 M AC = iAC .Z = S AC .Z 1 1 MAD = 4iAD.Z = SAD.Z 根据平衡条件: M AB+M AC+M AD =M S Aj Z = M 1 M S S M Aj AB AB = M S S M Aj AD AD = M S S M Aj AC AC = 注:1、M 将汇交于 A 结点各杆的转动刚度的比例分配给各杆的 A 端,转动刚度越大, 所承担的弯矩越大

:弯矩分配系数 2、S Mu=4M分配弯矩记为M 3、∑4g=1 4、根据传递系数:Ma4=0Mc=-Mac Mp4=1/2MD M:传递弯矩 推 §9-3力矩分配法的基本原理 任意荷载下单结点的超静定梁、刚架: 1、单结点刚架: 采用叠加法 采用位移法计算时:,乙,+R=0 自由项:Rp=M5+M5+M在=∑M5刚臂反力矩:等于汇交于结点的各杆杆端固 端弯矩的代数和,即各固端弯矩所不能平衡的差额,又称.不平衡力矩 系数:1=42+33+i4=S2+S,+S4=∑S汇交于结点的各杆端劲度系数的总 和 乙=-R/-∑M 各近端弯矩:由叠加M=-Mp+M,Z, M2=M5+S -∑M=M5+4.人∑M) ∑S M=M5+S-L-Mg+,(EM) ∑S -M近=Mi+人∑Mg) 固端弯矩与分配弯矩之和、分配系数 远端弯矩: M,=M5+6s+6Σ0
2、 = k Ak Aj Aj S S -弯矩分配系数 M AJ = u Aj .M 分配弯矩 记为 u M Aj 3、 = A u Aj 1 4、根据传递系数: MBA = 0 MCA = −M AC MDA 2MAD =1/ C M jA :传递弯矩 推广 §9-3 力矩分配法的基本原理 任意荷载下单结点的超静定梁、刚架: 1、单结点刚架: 采用叠加法 采用位移法计算时: r11Z1 + R1P = 0 自由项: = + + = F j F F F R1P M12 M13 M14 M1 刚臂反力矩:等于汇交于结点的各杆杆端固 端弯矩的代数和,即各固端弯矩所不能平衡的差额,又称.不平衡力矩。 系数: = + + = S + S + S =S j r i i i 11 4 12 3 13 14 12 13 14 1 汇交于结点的各杆端劲度系数的总 和 − = − = j F j P S M r R Z 1 1 11 1 1 各近端弯矩:由叠加 M = M P + M1Z1 ( ) = + − − = + F j F j F F j M u M S M M M S 12 12 1 1 1 12 12 12. . ( ) = + − − = + F j F j F F j M u M S M M M S 13 13 1 1 1 13 13 13. . ( ) = + − − = + F j F j F F j M u M S M M M S 14 14 1 1 1 14 14 14. . 固端弯矩与分配弯矩之和、分配系数 远端弯矩: ( ) = + − − = + F j F j F F j M C u M S M M M C S 21 12 12 1 1 1 21 21 12 12 . . .

MaM+Cu SpC) ∑S M=Mi+CuS4 -∑M=M+C4人∑M写) 固端弯矩与传递弯矩之和、传 ∑S 递系数 2、根据上述结构,总结过程: ①、固定结点:加入刚臂,此时各杆端有固端弯矩,而结点上有不平衡弯矩,它暂时由 刚臂承受: ②、放松结点:取消刚臂,让结点转动。相当于在结点上加入一个反号的不平衡力矩, 于是不平衡力矩被消除而结点获得平衡。此反号的不平衡力矩将按劲度系数大小的比例 分配给各近端,于是各近端弯矩等于固端弯矩与分配弯矩之和,而远端弯矩等于固端弯 矩与传递弯矩之和。 §9-4用力矩分配法计算连续梁和无侧移刚架 对于只有一个结点角位移,一次放松就可消除刚臂,因此结果为精确解。对具有两个以 上结点角位移的连续梁和刚架,可以采用逐个结点轮流放松的办法,把各结点约束力矩 轮流进行分配、传递,直到各结点约束力矩小到可略去不计。再叠加。 力矩分配法解题步骤: 1)固端弯矩:各转角位移对应刚结点分配及传递系数 2)放松一转角,分配、传递(only one) 3)放松另一转角(固定刚放松的),分配,传递 4)多个依次 5)第二轮循环 6)第三、四.循环 7)叠加最后弯矩=每个杆端 8)校核等截面杆件组成的连续梁和无侧移刚架 (MM):(MM-M)
( ) = + − − = + F j F j F F j M C u M S M M M C S 31 13 13 1 1 1 31 31 13 13 . . . . ( ) = + − − = + F j F j F F j M C u M S M M M C S 41 14 14 1 1 1 41 41 14 14 . . . . 固端弯矩与传递弯矩之和、传 递系数 2、根据上述结构,总结过程: ①、固定结点:加入刚臂,此时各杆端有固端弯矩,而结点上有不平衡弯矩,它暂时由 刚臂承受; ②、放松结点:取消刚臂,让结点转动。相当于在结点上加入一个反号的不平衡力矩, 于是不平衡力矩被消除而结点获得平衡。此反号的不平衡力矩将按劲度系数大小的比例 分配给各近端,于是各近端弯矩等于固端弯矩与分配弯矩之和,而远端弯矩等于固端弯 矩与传递弯矩之和。 §9-4 用力矩分配法计算连续梁和无侧移刚架 对于只有一个结点角位移,一次放松就可消除刚臂,因此结果为精确解。对具有两个以 上结点角位移的连续梁和刚架,可以采用逐个结点轮流放松的办法,把各结点约束力矩 轮流进行分配、传递,直到各结点约束力矩小到可略去不计。再叠加。 力矩分配法解题步骤: 1)固端弯矩:各转角位移对应刚结点分配及传递系数 2)放松一转角,分配、传递(only one) 3)放松另一转角(固定刚放松的),分配,传递 4)多个依次 5)第二轮循环 6)第三、四.循环 7)叠加最后弯矩=每个杆端 8)校核 等截面杆件组成的连续梁和无侧移刚架 ) :. : :. 2 1 ) : ( 2 1 ( i k ki i j j i i k i j M − M M − M = i i
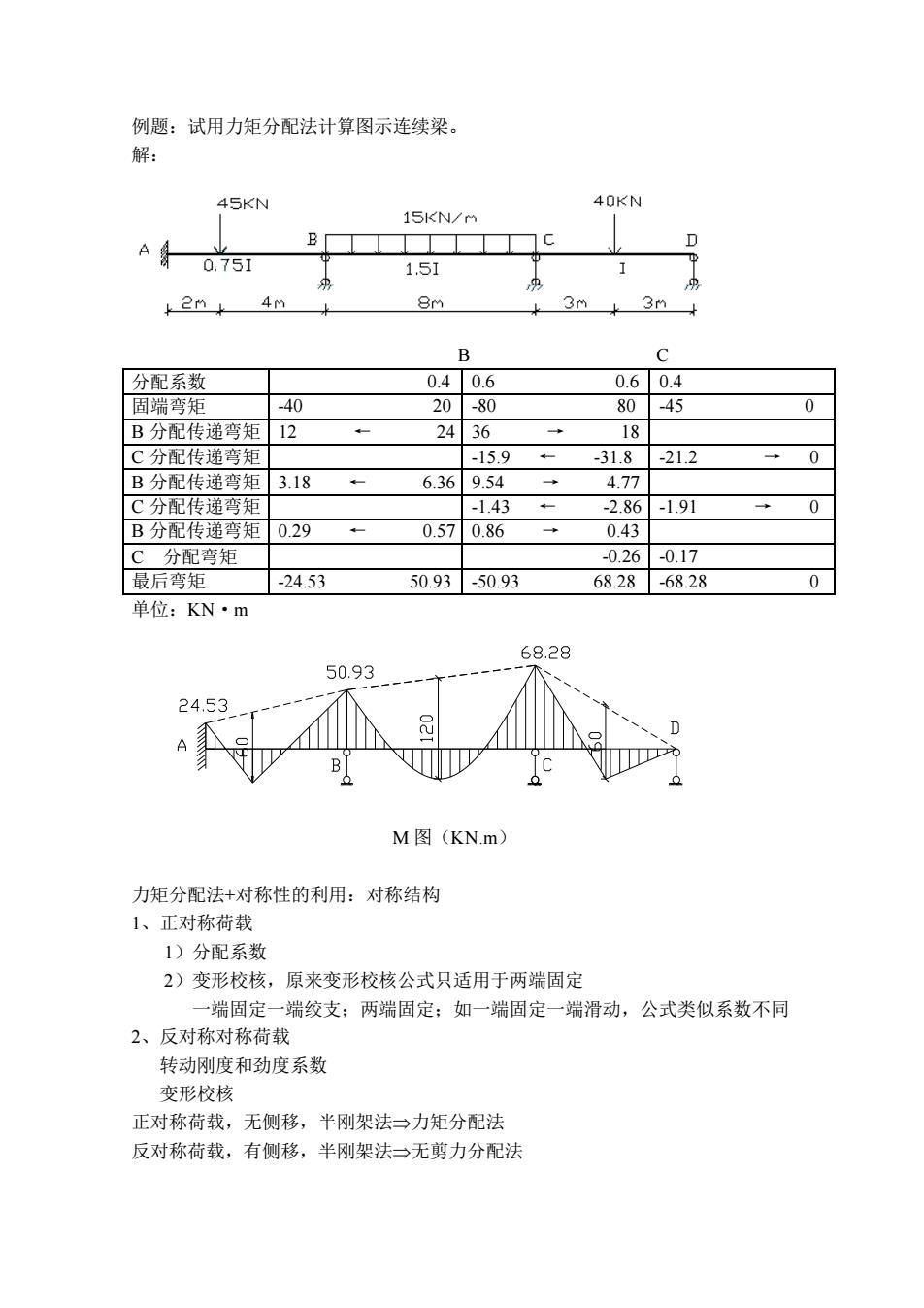
例题:试用力矩分配法计算图示连续梁。 解: 45KN 40KN 15KN/m A B 0.751 1.51 4m 8m 3m B 0406 0604 周端弯矩 40 20-80 80 4 0 B分配传递弯矩12 2436 18 C分配传递弯矩 .150 218 212 0 B分配传递弯矩3.18 6.369.54 4.77 C分配传递 -1.43 2.86-1.91 B分配传递弯矩0.29 0.570.86 0.43 C分配弯矩 -026017 最后弯矩 -24.53 5093-5093 68.28 -68.28 单位:KN·m 50.93 M图(KN.m 力矩分配法+对称性的利用:对称结构 1、正对称荷载 1)分配系数 2)变形校核,原来变形校核公式只适用于两端固定 一端固定一端纹支:两端固定:如一端固定一端滑动,公式类似系数不同 2、反对称对称荷载 转动刚度和劲度系数 变形校核 正对称荷载,无侧移,半刚架法→力矩分配法 反对称荷载,有侧移,半刚架法一无剪力分配法
例题:试用力矩分配法计算图示连续梁。 解: B C 分配系数 0.4 0.6 0.6 0.4 固端弯矩 -40 20 -80 80 -45 0 B 分配传递弯矩 12 ← 24 36 → 18 C 分配传递弯矩 -15.9 ← -31.8 -21.2 → 0 B 分配传递弯矩 3.18 ← 6.36 9.54 → 4.77 C 分配传递弯矩 -1.43 ← -2.86 -1.91 → 0 B 分配传递弯矩 0.29 ← 0.57 0.86 → 0.43 C 分配弯矩 -0.26 -0.17 最后弯矩 -24.53 50.93 -50.93 68.28 -68.28 0 单位:KN·m M 图(KN.m) 力矩分配法+对称性的利用:对称结构 1、正对称荷载 1)分配系数 2)变形校核,原来变形校核公式只适用于两端固定 一端固定一端绞支;两端固定;如一端固定一端滑动,公式类似系数不同 2、反对称对称荷载 转动刚度和劲度系数 变形校核 正对称荷载,无侧移,半刚架法力矩分配法 反对称荷载,有侧移,半刚架法无剪力分配法
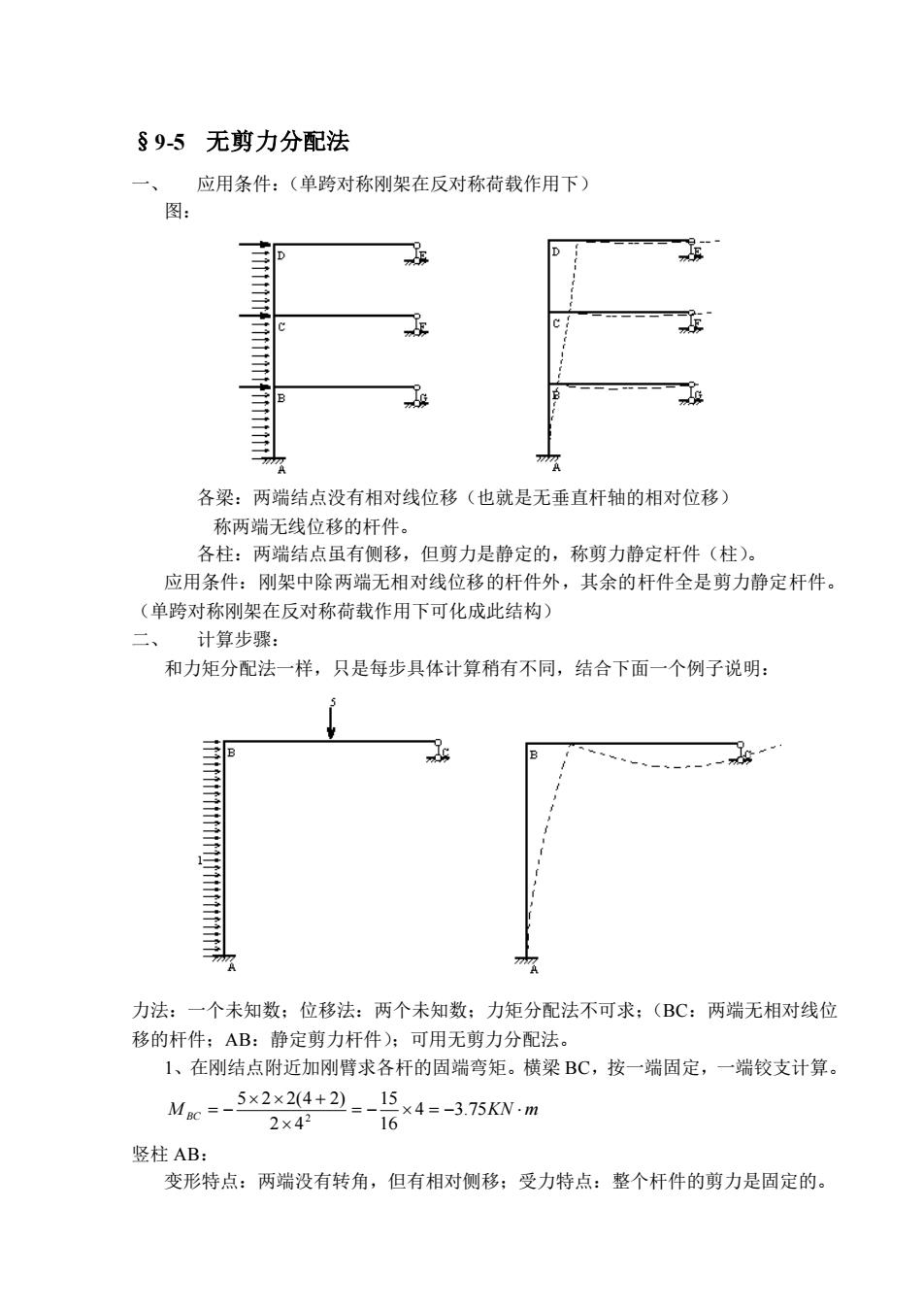
§9-5无剪力分配法 应用条件:(单跨对称刚架在反对称荷载作用下) 图: 各梁:两端结点没有相对线位移(也就是无垂直杆轴的相对位移) 称两端无线位移的杆件。 各柱:两端结点虽有侧移,但剪力是静定的,称剪力静定杆件(柱)。 应用条件:刚架中除两端无相对线位移的杆件外,其余的杆件全是剪力静定杆件 (单跨对称刚架在反对称荷载作用下可化成此结构) 二、 计算步骤: 和力矩分配法一样,只是每步具体计算稍有不同,结合下面一个例子说明: 力法:一个未知数:位移法:两个未知数:力矩分配法不可求:(BC:两端无相对线位 移的杆件;AB:静定剪力杆件):可用无剪力分配法。 1、在刚结点附近加刚臂求各杆的固端弯矩。横梁BC,按一端固定,一端铰支计算 Me-5224+2-启4=-375Nm 2×42 竖柱AB: 变形特点:两端没有转角,但有相对侧移:受力特点:整个杆件的剪力是固定的
§9-5 无剪力分配法 一、 应用条件:(单跨对称刚架在反对称荷载作用下) 图: 各梁:两端结点没有相对线位移(也就是无垂直杆轴的相对位移) 称两端无线位移的杆件。 各柱:两端结点虽有侧移,但剪力是静定的,称剪力静定杆件(柱)。 应用条件:刚架中除两端无相对线位移的杆件外,其余的杆件全是剪力静定杆件。 (单跨对称刚架在反对称荷载作用下可化成此结构) 二、 计算步骤: 和力矩分配法一样,只是每步具体计算稍有不同,结合下面一个例子说明: 力法:一个未知数;位移法:两个未知数;力矩分配法不可求;(BC:两端无相对线位 移的杆件;AB:静定剪力杆件);可用无剪力分配法。 1、在刚结点附近加刚臂求各杆的固端弯矩。横梁 BC,按一端固定,一端铰支计算。 M BC = − = − KN m + = − 4 3.75 16 15 2 4 5 2 2(4 2) 2 竖柱 AB: 变形特点:两端没有转角,但有相对侧移;受力特点:整个杆件的剪力是固定的

QAB-=0 受力状态类似于:下端固定,上端滑动的杆件, 它的固端弯矩可有表10-1查出 Mm=-月×1x16=-53KN.m Mu=-石92=-2.67KN:m B点不平衡力矩:-6.42KNm 也就是在B附加刚臂,人为加上-6.42KNm的力矩,而B点无外力矩作用,保持 致,消去这一不平衡力矩(在刚结点和反向不平衡力矩加上一个结点力偶)。 2、放松结点,求各杆的分配弯矩和传递弯矩。 1)先求转动刚度(劲度系数,转角位移方程中转角的系数)及分配系数,传递系数 横梁:S=3i1=12 竖柱:SBA=i2=3 原因: BA:变形特点,结点B既有转角同时也有侧移:受力特点,各截面剪力均为零, 因而各截面的弯矩为一常数。 这种杆件叫零剪力杆件。受力状态如图所示悬臂杆。当B端转动0B时,杆端力偶 为MBA=iBA0B,MBA=MAB 主要结论:零剪力杆件的转动刚度(劲度系数)为SAB=B,传递系数CA二】 总之:1)在结点力偶作用下,刚架中的剪力静定杆件都是零剪力杆件。因此,放松 结点时(结点既转动又侧移),这些杆件都是在零剪力的条件下得到分配弯矩和传递弯 矩,故称:无剪力分配。uBC-0.8,uBA=0.2,CBA=l,CBC0。 2)不平衡力矩的分配和传递: 3)叠加出各杆端弯矩,作M图 1 13 3、前力静定杆件的固岩弯矩 对刚架中任何形式的剪力静定杆件,求固端弯矩的步 骤: 先根据静力平衡条件求出杆端剪力,然后将杆端剪力看 作杆端荷载,按该端滑动另一端固定的杆件进行计算。 直接利用公式(P54,11-7)静定剪力杆件的修正周端 弯矩。 4、零剪力杆件的转动刚度和传递系数(劲度系数) 零剪力杆件在结点力偶作用下受力状态类似于一端固定一端自由的悬臂杆
QAB=0 B 点不平衡力矩:-6.42KN·m 也就是在 B 附加刚臂,人为加上-6.42KN·m 的力矩,而 B 点无外力矩作用,保持一 致,消去这一不平衡力矩(在刚结点和反向不平衡力矩加上一个结点力偶)。 2、放松结点,求各杆的分配弯矩和传递弯矩。 1)先求转动刚度(劲度系数,转角位移方程中转角的系数)及分配系数,传递系数 横梁:SBC=3i1=12 竖柱:SBA=i2=3 原因: BA:变形特点,结点 B 既有转角同时也有侧移;受力特点,各截面剪力均为零, 因而各截面的弯矩为一常数。 这种杆件叫零剪力杆件。受力状态如图所示悬臂杆。当 B 端转动θB时,杆端力偶 为 MBA=iBA·θB,MBA=-MAB 主要结论:零剪力杆件的转动刚度(劲度系数)为 SAB=iBA ,传递系数 CBA=-1 总之:1)在结点力偶作用下,刚架中的剪力静定杆件都是零剪力杆件。因此,放松 结点时(结点既转动又侧移),这些杆件都是在零剪力的条件下得到分配弯矩和传递弯 矩,故称:无剪力分配。μBC=0.8,μBA=0.2,CBA=-1,CBC=0。 2)不平衡力矩的分配和传递; 3)叠加出各杆端弯矩,作 M 图 3、剪力静定杆件的固端弯矩 对刚架中任何形式的剪力静定杆件,求固端弯矩的步 骤: 先根据静力平衡条件求出杆端剪力,然后将杆端剪力看 作杆端荷载,按该端滑动另一端固定的杆件进行计算。 直接利用公式(P54,11-7)静定剪力杆件的修正固端 弯矩。 4、零剪力杆件的转动刚度和传递系数(劲度系数) 零剪力杆件在结点力偶作用下受力状态类似于一端固定一端自由的悬臂杆。 受力状态类似于:下端固定,上端滑动的杆件, 它的固端弯矩可有表 10-1 查出 M AB = − 116 = −5.33KN m 3 1 M BA = − ql = −2.67KN m 6 1 2

修正:劲度系数,传递系数 横梁按一端固定一端铰支计算
修正:劲度系数,传递系数 横梁按一端固定一端铰支计算