
第一章质点力学 质点速度、加速度的分量表示; 质点运动微分方程; 质点动力学的三个基本定理与基本守恒定律。 求解动力学问题的步骤: 1.受力分析 2.分析运动状况,选取适当的坐标系物理问题→数学问题物 3根据牛顿第二定律等建立方程. 4.解方程. }求数学问题的解 数 ↓ 5对结果进行必要的讨论, }阐明解的物理意义 物
求解动力学问题的步骤 : 1.受力分析. 2.分析运动状况,选取适当的坐标系. 3.根据牛顿第二定律等建立方程. 物理问题 数学问题 4.解方程. 5.对结果进行必要的讨论. 求数学问题的解 阐明解的物理意义 物数物 第一章 质点力学 质点速度、加速度的分量表示; 质点运动微分方程; 质点动力学的三个基本定理与基本守恒定律

第二章 质点系力学 §2.1质点系 定义:一群相互作用着的质点称为质点系。 一、质点系的内力和外力 内力:质点系中质点间的相互作用力。 外力:质点系以外的物体对质点系内 质点的作用力。 (孤立系或封闭系) 内力的特征:质点系内力的矢量和为零。 F(i)= 2 =0 i=1
第二章 质点系力学 §2.1质点系 定义:一群相互作用着的质点称为质点系。 一、质点系的内力和外力 内力:质点系中质点间的相互作用力。 外力:质点系以外的物体对质点系内 质点的作用力。 n i j ij f G ji f G )( 1 e F G )( 2 e F G (孤立系或封闭系) 内力的特征:质点系内力的矢量和为零。 0 1 1 )( = ∑ ∑ = = ≠ = n i n ijj ij i F f G G
二、质心 m 将各质点的质量乘以其位 矢并求和有 mi+m23++m+. +m,7=∑m听 i=l 以m表示质点系的总质量,则m=∑m i=1 对质点系我们总能找到一个定点C,使得: m=∑m, m i=1 称产。为质点系的质 量中心,简称质心。 m ∑m i=
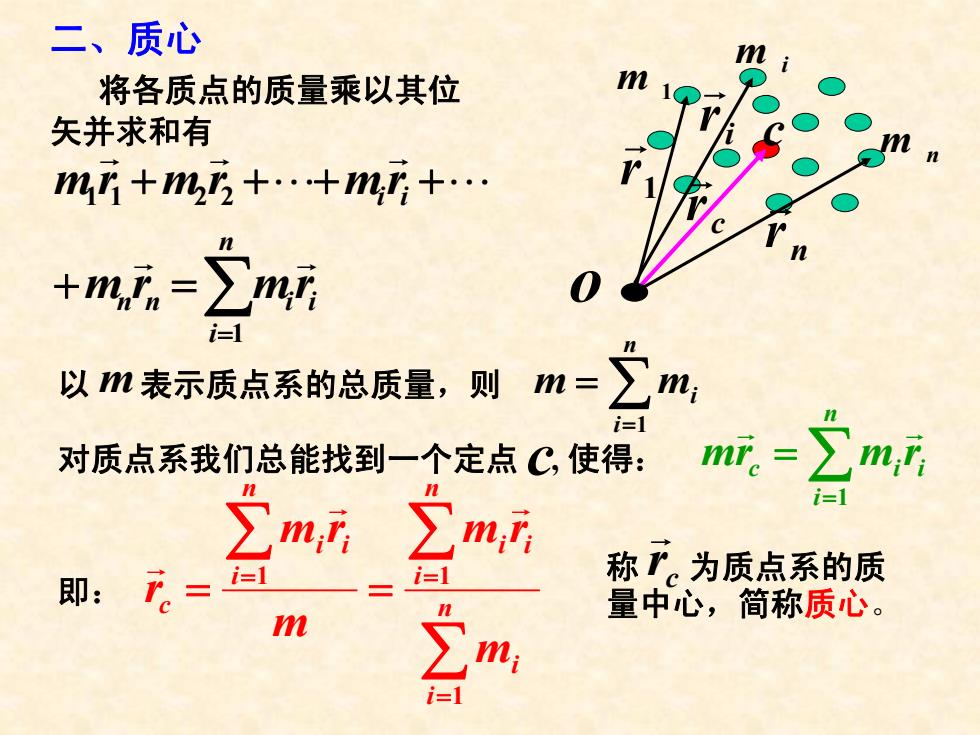
二、质心 m n m 1 m i c o n r G i r G c r G 1 r G 将各质点的质量乘以其位 矢并求和有 ∑= =+ ++++ n i nn ii ii rmrm rmrmrm 1 2211 GG " G " G G 对质点系我们总能找到一个定点 c, 使得: ∑= = n i c iirmrm 1 G G 以 表示质点系的总质量,则 m ∑= = n i mm i 1 即: ∑ ∑∑ = = = == n i i n i ii n i ii c m rm m rm r 1 1 1 G G G 称 为质点系的质 量中心,简称质心 。 c r G

mF m m 在直接坐标系下: ∑m mxi miyi m;Zi xC= yc= Zc= m mi mi i=1 i= i=1 当质量连续分布时,应将求和改为积分,即 m dm
, 1 1 ∑ ∑ = = = n i i n i ii C m xm x ∑ ∑ = = = n i i n i ii C m zm z 1 1 , 1 1 ∑ ∑ = = = n i i n i ii C m ym y 在直接坐标系下: 当质量连续分布时,应将求和改为积分,即 ∫ ∫∫ == dm dmr m dmr rc G G G ∑ ∑∑ = = = == n i i n i ii n i ii c m rm m rm r 1 1 1 G G G

说明: (1)几何形状对称的均质物体,质心就是几何对称中心。 (2)有些物体的质心可能不在所研究的物体上。 (3)质心和重心是两个不同的概念
说明∶ (2)有些物体的质心可能不在所研究的物体上。 (3)质心和重心是两个不同的概念。 (1)几何形状对称的均质物体,质心就是几何对称中心

§2.2动量定理与动量守恒定律 一、动量定理 dn mi dt2 =F(+F( (i=1,2.,n) 将上几方程迭加起来得 店-立+ i=l i=1 i=l d2i= F”=0,m i=1 i=1 dt 0-2m dt 质点系的动量定理。 i=1
§2.2动量定理与动量守恒定律 一、动量定理 ),2,1( )()( 2 2 niFF dt rd m i i e i i i " G G G += = )( 1 )( 1 2 2 1 i i n i e i n i i n i i FF dtrd m G G G ∑∑∑= = = += ( ) 1 2 2 1 ∑ ∑ = = = = n i ii i n i i vmp dtpd dtrd m G G G G ,0 1 )( ∑= = n i i F i G ∵ ∑= ∴ = n i e F i dt pd 1 )( G G ——质点系的动量定理。 将上 方程迭加起来得 n

dp F 质点系的动量定理。 d i-1 上式表明:质点系总动量对时间的微商等于作用在该质点系 的外力之矢量和。 在直接坐标系下: 迎x F dt dt d n dt dt "司 i=1 d迎 d dt dt ∑ 注意:内力不改变质点系的动量
∑= ∴ = n i e F i dt pd 1 )( G G ——质点系的动量定理。 上式表明:质点系总动量对时间的微商等于作用在该质点系 的外力之矢量和。 在直接坐标系下: ∑∑= = = = n i e ix n i ixi x Fvm dt d dt dp 1 )( 1 ∑∑= = = = n i e iy n i iyi y Fvm dt d dt dp 1 )( 1 ∑∑= = = = n i e iz n i izi z Fvm dt d dt dp 1 )( 1 注意:内力不改变质点系的动量

二、质心运动定理 因 m=mre, 故 ∑m,=m。 i=1 i=1 因此 m dvi dt i=1 i=1 即 m 质心运动定理 上式表明:质点系质量与其质心加速度的乘积等 于作用在该质点系的外力之矢量和
二、质心运动定理 , 1 c n i ii rmrm G G ∑ = = c n i ii 因 故 vmvm G G ∑ = =1 因此 ∑∑ = = = = n i e i n i i i c F dt vd m dt vd m 1 )( 1 G G G ∑ = = n i e i c F dt rd m 1 )( 2 2 G G 即 ——质心运动定理 上式表明:质点系质量与其质心加速度的乘积等 于作用在该质点系的外力之矢量和

=2 质心运动定理 i=1 说明:(①)质心的运动就好像一个质点的运动。 (2)外力已知时,由质心运动定理就可确定质心的运动, 内力对质心的运动无影响。 (3)质心运动定理不能描述各质点的运动情况。 (4)把实际物体抽象为质点,就是只考虑了质心的运动 而忽略了物体中各质点相对质心的运动
说明:(1) 质心的运动就好像一个质点的运动。 (2)外力已知时,由质心运动定理就可确定质心的运动, 内力对质心的运动无影响。 (3)质心运动定理不能描述各质点的运动情况。 (4)把实际物体抽象为质点,就是只考虑了质心的运动 而忽略了物体中各质点相对质心的运动。 ∑ = = n i e i c F dt rd m 1 )( 2 2 G G ——质心运动定理

三、动量守恒定律 当 F,e)=0时:由 dp ∑F)知 i=1 dt i=1 dp =0→币=∑m,=c(常矢量) dt i=1 质点系的动量守恒 :D=∑m,=m。.。=常矢量 i=1 结论:当外力之矢量和为零时,质点系的动量不变,而它的 质心做惯性运动。 注意:内力不改变质点系的动量,也不改变质点系质心的速度
三、动量守恒定律 = 0 dt pd G (常矢量) 1 cvmp n i ii G G G ∑ == = ∑ = = n i e Fi dtpd 1 )( G G 0 1 )( ∑ = =ni e Fi G 当 时: 由 知 c n i ii vmvmp G G G ∵ ∑ == =1 ∴vc = 常矢量 G ——质点系的动量守恒 结论:当外力之矢量和为零时,质点系的动量不变,而它的 质心做惯性运动。 注意:内力不改变质点系的动量,也不改变质点系质心的速度