
第六章原子猪构与元素周期性 6.1原子结构的近代概念 6.1.1Bohr原子模型 1.光和电磁辐射 光谱就是复合光经色散系统分光后 按波长大小依次排列的彩色图像,若复合 光含有各种波长的光,得到的应是连续光 谱,若复合光波长不齐全,只有少数几种 波长的光,经色散系统分光后,得到的就 是明暗相间的线状光谱
6.1.1 Bohr原子模型 光谱就是复合光经色散系统分光后, 按波长大小依次排列的彩色图像,若复合 光含有各种波长的光,得到的应是连续光 谱,若复合光波长不齐全,只有少数几种 波长的光,经色散系统分光后,得到的就 是明暗相间的线状光谱。 6.1 原子结构的近代概念 第六章 原子结构与元素周期性 1.光和电磁辐射
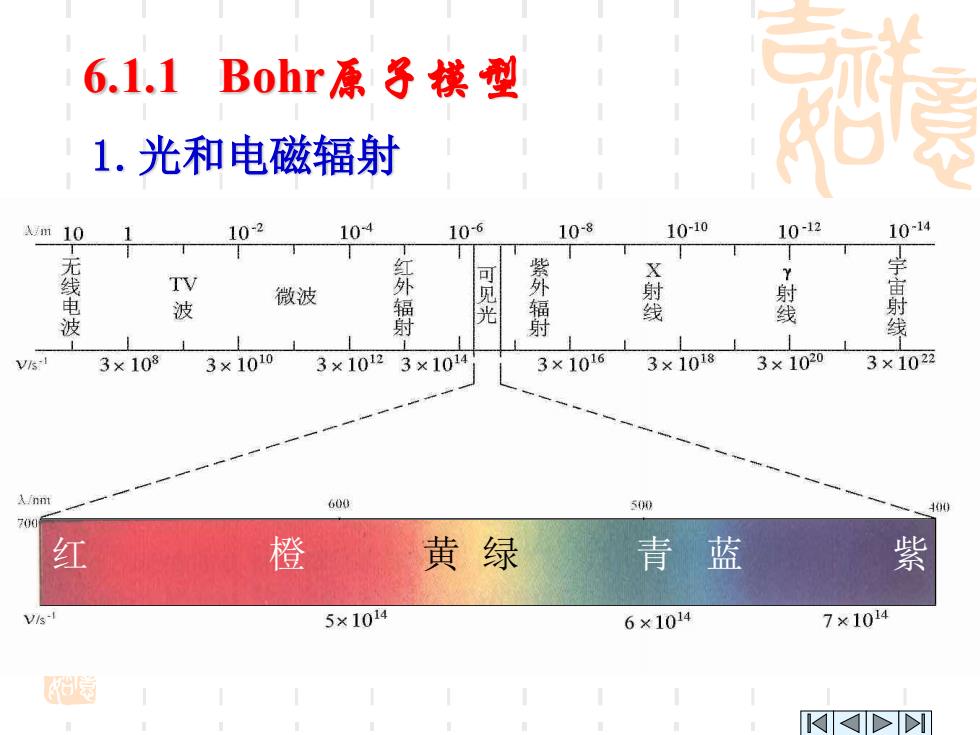
6.1.1 Bohr原子模型 1.光和电磁辐射 A/m 10 102 104 10-6 10-8 10-10 10-12 1014 无无 紫 线 TV 电 微波 波 线 波 光 3×1038 3×1010 3×10123×101 3×1016 3×1018 3×1020 3×1022 A/nn 600 500 706 红 橙黄绿 青蓝 紫 5×1014 6×1014 7×104
红 橙 黄 绿 青 蓝 紫 6.1.1 Bohr原子模型 1.光和电磁辐射
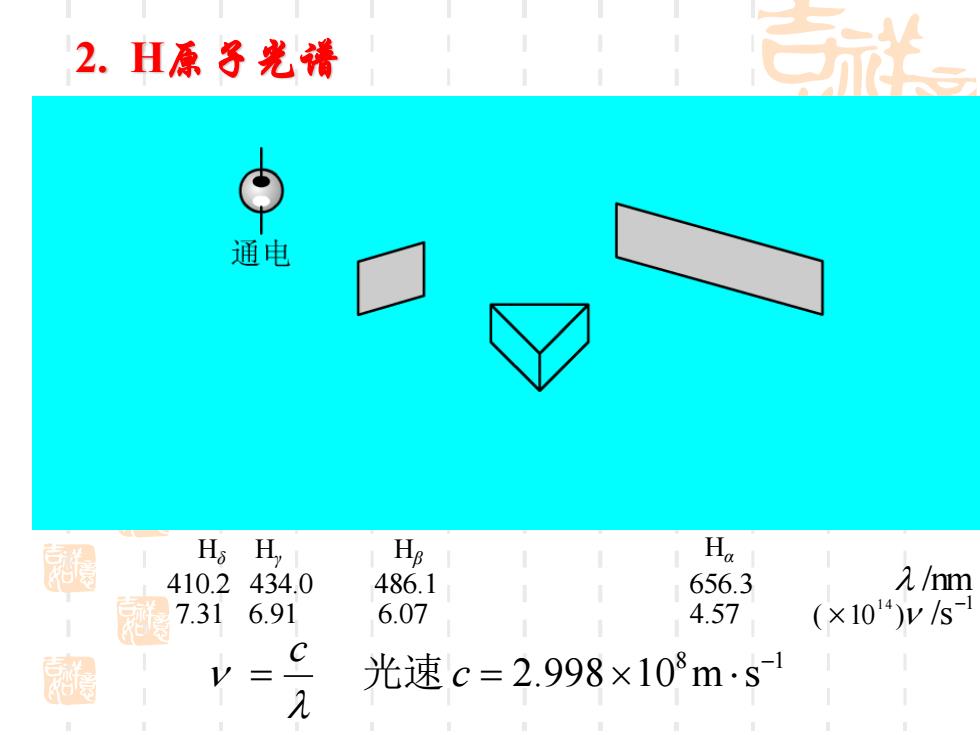
2.H原子光清 通电 墨 H.H Hg Ha 410.2 34.0 486.1 656.3 λm 1 7.31 6.91 6.07 4.57 (×1014)ys C 光速c=2.998×108m·s1 几
8 1 2.998 10 m s − = c = c 光速 Hα 656.3 4.57 Hβ 486.1 6.07 Hγ 434.0 6.91 Hδ 410.2 7.31 /nm1 ( 10 ) /s 1 4 − 2. H原子光谱
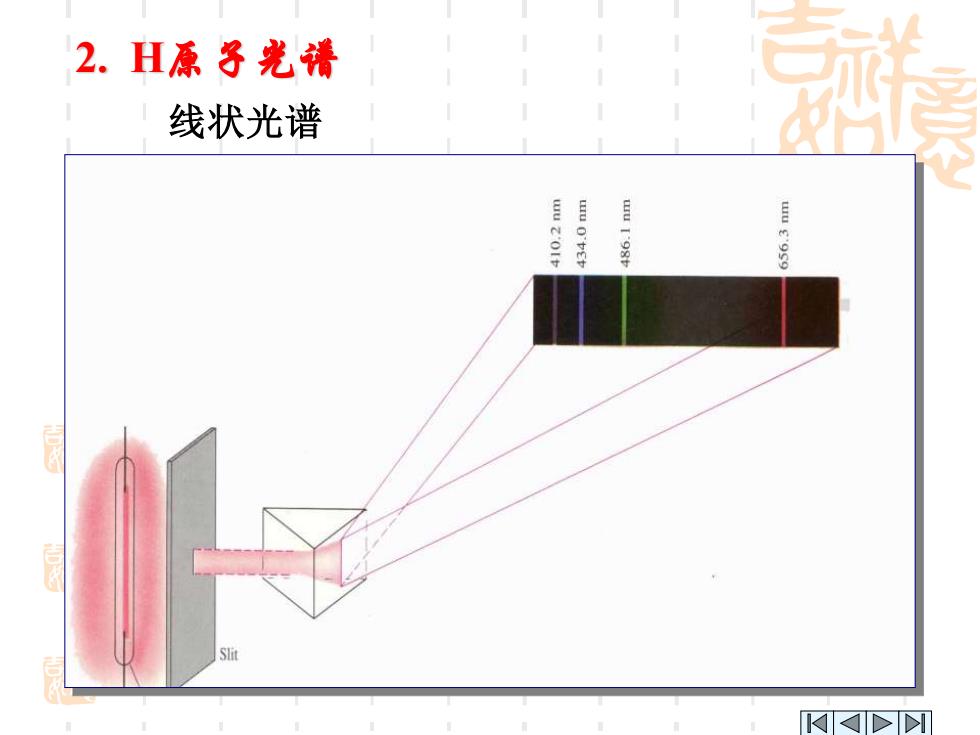
2.H原子光清 线状光谱 tu g'9so KKDD
线状光谱 2. H原子光谱

2.H原子光清 氢原子可见光谱 I
氢原子可见光谱 2. H原子光谱

2.H原子光清 H原子光谱具有以下特征:①是不连 续线状光谱,从红外到紫外呈现多条具有 特征波长的谱线;②从长波到短波,谱线 间的距离越来越小。 巴尔麦找出了H原子在可见光区谱线的 364600×n2 波长可由下式表示:= n2-4 思 后来,里德堡将其改进为 KKDN
H原子光谱具有以下特征:①是不连 续线状光谱,从红外到紫外呈现多条具有 特征波长的谱线;② 从长波到短波,谱线 间的距离越来越小。 4 364600 2 2 − n . n 巴尔麦找出了H原子在可见光区谱线的 波长可由下式表示: λ= 后来,里德堡将其改进为: ) 1 2 1 ( 1 2 2 n = RH − v = 2. H原子光谱

2.H原子光清 w:谱线波长的倒数,波数(cml). :大于2的正整数. R1:里德堡常数,1.09677576×107m1 n=3,14,5,6分别对应氢光谱中 超↓↓↓↓ Ha、Hg、HH.Balmer系 M✉D
v: 谱线波长的倒数, 波数(cm-1 ). n:大于2的正整数. RH:里德堡常数, 1.09677576107m-1 n = 3, 4 , 5, 6 分别对应氢光谱中 ↓ ↓ ↓ ↓ H、H、H、H、 Balmer系 2. H原子光谱
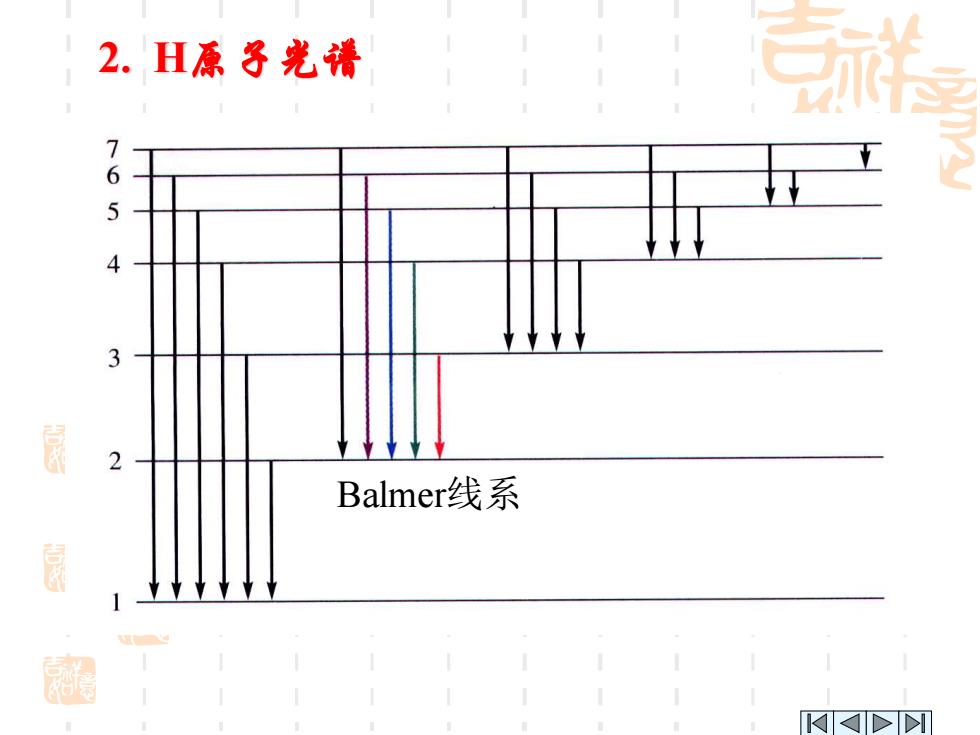
2.H原子光清 7 6 5 2 Balmer?线系 鼠 >
Balmer线系 2. H原子光谱

2.H原子光清 在某一瞬间,一个氢原子只能产生一 条谱线,许多氢原子才能放出不同的谱线。 这些不同的谱线可用通式表示 v=R(2 2 n, n1、n2为正整数,且n,<n,当n1-2时为 巴尔麦系;n=3时得到氢的红外光谱,称 为帕邢系;n=1时得到氢的紫外光谱,称 为拉曼系
在某一瞬间,一个氢原子只能产生一 条谱线,许多氢原子才能放出不同的谱线。 这些不同的谱线可用通式表示: ) 1 1 ν ( 2 2 2 1 H n n = R − n1、n2为正整数,且n1<n2当n1=2时为 巴尔麦系;n1=3时得到氢的红外光谱,称 为帕邢系;n1=1时得到氢的紫外光谱,称 为拉曼系。 2. H原子光谱

6.1.1 Bohr原子模型 ① 氢原子核外电子处在一定 VT A 的线性轨道上绕核运行,氢原子 核外电子不是在任意轨道上运动 而是在符合一定条件的轨道上运 动,既不放出能量也不吸收能量, 这种状态称为稳定态简称定态 原子可以有许多定态,其中能量 最低的定态称为基态,其余的定 态称为激发态;
① 氢原子核外电子处在一定 的线性轨道上绕核运行;氢原子 核外电子不是在任意轨道上运动, 而是在符合一定条件的轨道上运 动,既不放出能量也不吸收能量, 这种状态称为稳定态简称定态, 原子可以有许多定态,其中能量 最低的定态称为基态,其余的定 态称为激发态; 6.1.1 Bohr原子模型