
工程光学 第十章 光的电磁理论基础
第十章 光的电磁理论基础

重点: ·电磁波的平面波解 一平面波、简谐波解的形式和意义,物 理量的关系 ·光波的叠加
# 重点: • 电磁波的平面波解 –平面波、简谐波解的形式和意义,物 理量的关系 • 光波的叠加

散度在笛卡儿坐标系中的表达形式: V.A= 4+d4+a4 O 旋度在笛卡儿坐标系中的表达形式: to" V×A= to A
# 散度在笛卡儿坐标系中的表达形式: z A y A x A A x y z + + = 旋度在笛卡儿坐标系中的表达形式: x y z x y z A A A x y z e e e A =

·19世纪60年代,Maxwe I I建立经典电磁理论,从而 导致了电磁波的发现。同时,他把光学现象和电 磁现象联系起来,指出光也是一种电磁波,从而 产生光的电磁理论,并被后来的实验所证实。 o 电磁波在不同介质的界面上发生反射和折射现象, 在传播中出现干涉、衍射和偏振现象,而根据当 时已有的知识,光波也具有完全相似的干涉、衍 射和偏振等现象,它们之间有什么联系呢?电磁 波在真空中的速度
# • 19世纪60年代,Maxwell建立经典电磁理论,从而 导致了电磁波的发现。同时,他把光学现象和电 磁现象联系起来,指出光也是一种电磁波,从而 产生光的电磁理论,并被后来的实验所证实。 • 电磁波在不同介质的界面上发生反射和折射现象, 在传播中出现干涉、衍射和偏振现象,而根据当 时已有的知识,光波也具有完全相似的干涉、衍 射和偏振等现象,它们之间有什么联系呢?电磁 波在真空中的速度 0 0 c 1 =

麦克斯韦方程组在电磁学中的地位 如同牛顿运动定律在力学中的地位 一样。以麦克斯韦方程组为核心的 电磁理论,是经典物理学最引以自 豪的成就之一。它所揭示出的电磁 相互作用的完美统一,为物理学家 树立了这样一种信念:物质的各种 相互作用在更高层次上应该是统 的。另外,这个理论被广泛地应用 到技术领域
# 麦克斯韦方程组在电磁学中的地位, 如同牛顿运动定律在力学中的地位 一样。以麦克斯韦方程组为核心的 电磁理论,是经典物理学最引以自 豪的成就之一。它所揭示出的电磁 相互作用的完美统一,为物理学家 树立了这样一种信念:物质的各种 相互作用在更高层次上应该是统一 的。另外,这个理论被广泛地应用 到技术领域
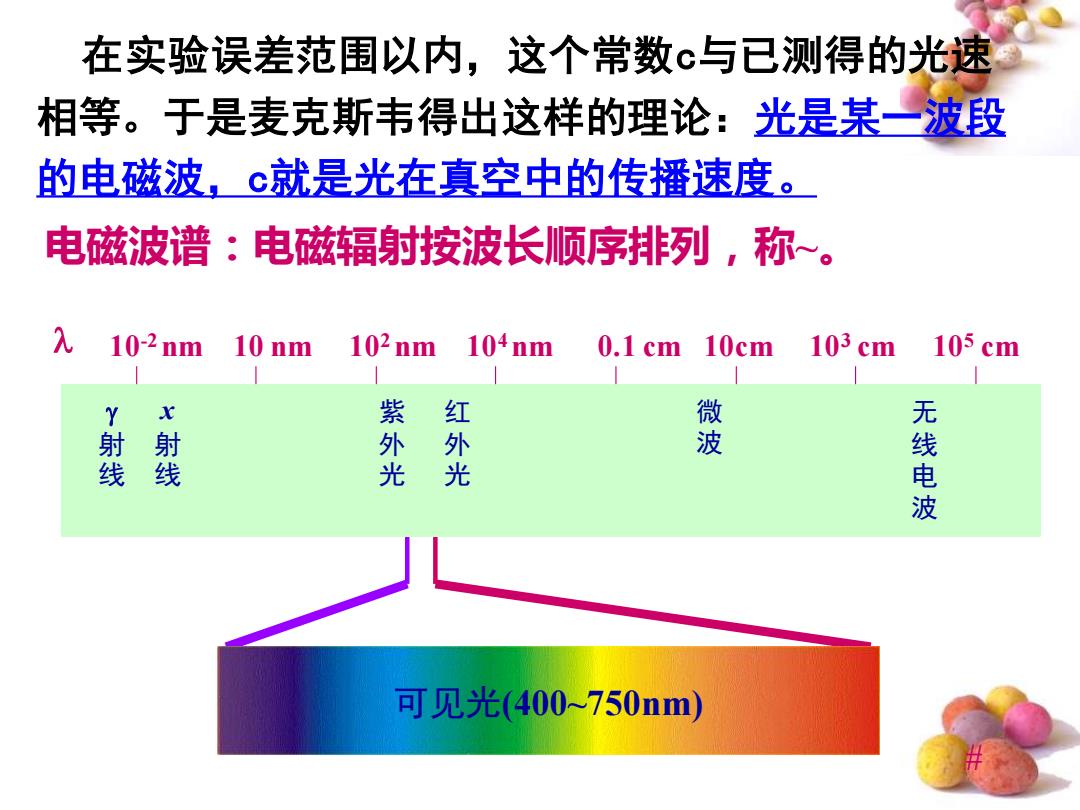
在实验误差范围以内,这个常数c与已测得的光速 相等。于是麦克斯韦得出这样的理论:光是某一波段 的电磁波,c就是光在真空中的传播速度。 电磁波谱:电磁辐射按波长顺序排列,称~。 10-2nm 10 nm 102nm104nm 0.1 cm 10cm 103 cm 105cm Y r 紫 红 微 无 波 线 线 光 光 農 可见光(400~750nm)
# 在实验误差范围以内,这个常数c与已测得的光速 相等。于是麦克斯韦得出这样的理论:光是某一波段 的电磁波,c就是光在真空中的传播速度。 电磁波谱:电磁辐射按波长顺序排列,称~。 可见光(400~750nm) 射 线 x 射 线 紫 外 光 红 外 光 微 波 无 线 电 波 10-2 nm 10 nm 102 nm 104 nm 0.1 cm 10cm 103 cm 105 cm

射线→x射线→紫外光→可见光→红外光一→微波→无线电波 光波的几何描述: 波动所存在的空间称为波场; 通常把某一时刻振动相位相同各点的轨迹称为 波面; 把能量传播的路径称为波线。 在各向同性的介质中,波线与波面处处正交
# 光波的几何描述: 波动所存在的空间称为波场; 通常把某一时刻振动相位相同各点的轨迹称为 波面; 把能量传播的路径称为波线。 在各向同性的介质中,波线与波面处处正交。 γ射线→ x 射线→紫外光→可见光→红外光→微波→无线电波

光的电磁性质 一、麦克斯韦方程组 7●D=p 3、法拉第电磁感应定律,变化 V●B=0 的磁场产生感应的电场。 VxE=- OB 4、安培全电流定律。 8t ap V×i=j+ 8t 1、电场的高斯定理,表示电场是一个有源场。 2、磁通连续定律,穿过一个闭合面的磁通量 等于零
# 光的电磁性质 一、麦克斯韦方程组 D B 0 B E D H t J t • = • = = − = + 1、电场的高斯定理,表示电场是一个有源场。 2、磁通连续定律,穿过一个闭合面的磁通量 等于零。 3、法拉第电磁感应定律,变化 的磁场产生感应的电场。 4、安培全电流定律

0: 封闭曲面内的电荷密度; j:积分闭合回路上的传导电流密度; ap 位移电流密度。 Ot 物质方程 描述物质在场作用下特性的关系式称为物质方程。 静止的、各向同性的介质中的物质方程存在以下关 系:
# D t :封闭曲面内的电荷密度; J:积分闭合回路上的传导电流密度; :位移电流密度。 物质方程 描述物质在场作用下特性的关系式称为物质方程。 静止的、各向同性的介质中的物质方程存在以下关 系:

J=cE σ是电导率 D=aE E是介电常数(或电容率) B=uH μ是磁导率 在各向同性均匀介质中,£、μ是常数,0=0。在真 空中 6=6。=8.8542×10-12C2/N.m2,4=4,=4π×10-7N.S2/C2 对于非磁性物质,4=山o
# J E = σ是电导率 D E = ε是介电常数(或电容率) B H = μ是磁导率 在各向同性均匀介质中,ε、μ是常数,σ=0。在真 空中 12 2 2 7 2 2 0 0 8.8542 10 / , 4 10 / C N m N S C − − = = = = 对于非磁性物质, = 0