
第四章 平面与平面系统 第一节平面镜成像 第二节 平行平板 第三节反射棱镜 第四节 折射棱镜与光楔
第一节 平面镜成像 第二节 平行平板 第三节 反射棱镜 第四节 折射棱镜与光楔 第四章 平面与平面系统
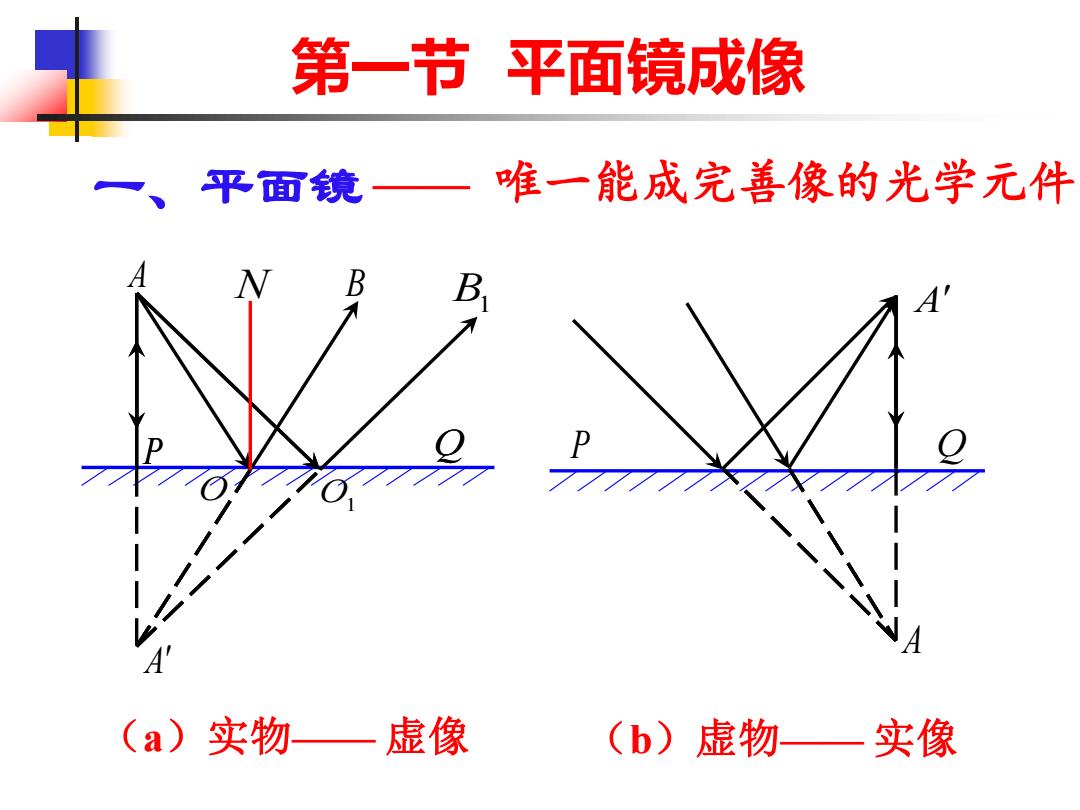
第一节平面镜成像 、 平面镜—唯一能成完善像的光学元件 B (a)实物—虚像 (b)虚物—实像
第一节 平面镜成像 一、平面镜 O1 P A N O A B1 B P Q (a)实物—— 虚像 A A P Q (b)虚物—— 实像 —— 唯一能成完善像的光学元件
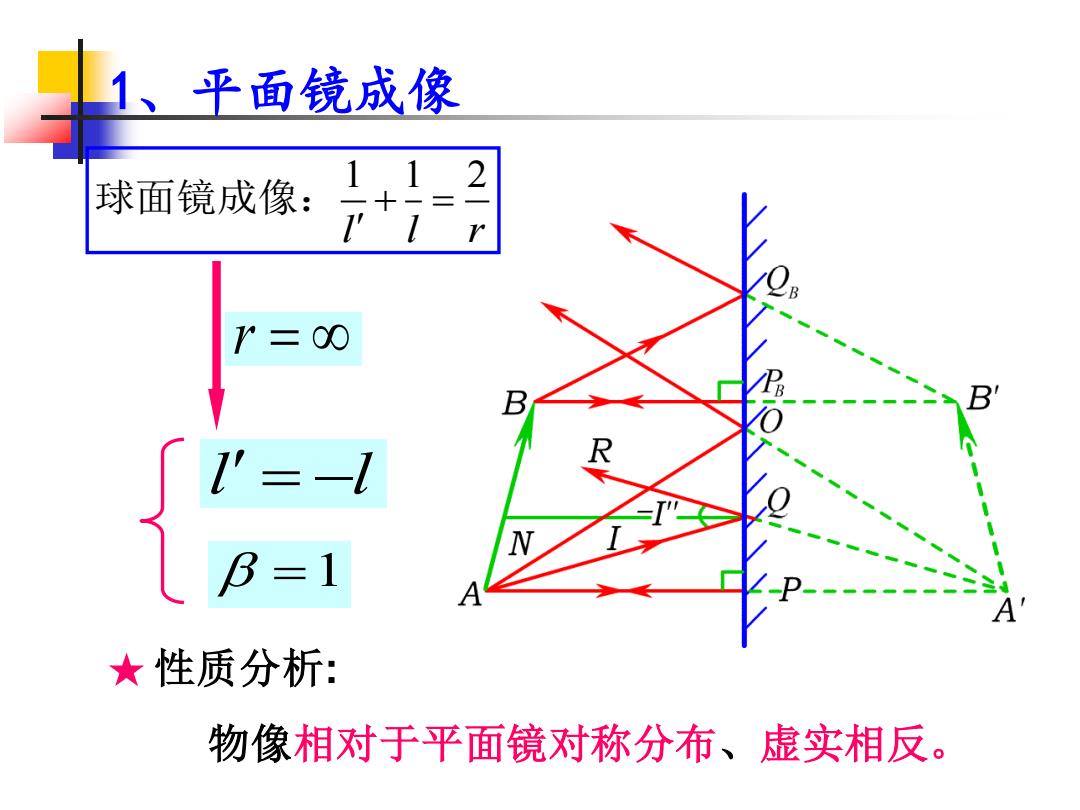
1、平面镜成像 球面镜成像: 1,1 2- =00 B ★性质分析: 物像相对于平面镜对称分布、虚实相反
1、平面镜成像 1 1 2 l l r + = 球面镜成像: ★ 性质分析: 物像相对于平面镜对称分布、虚实相反。 r = l l = − =1
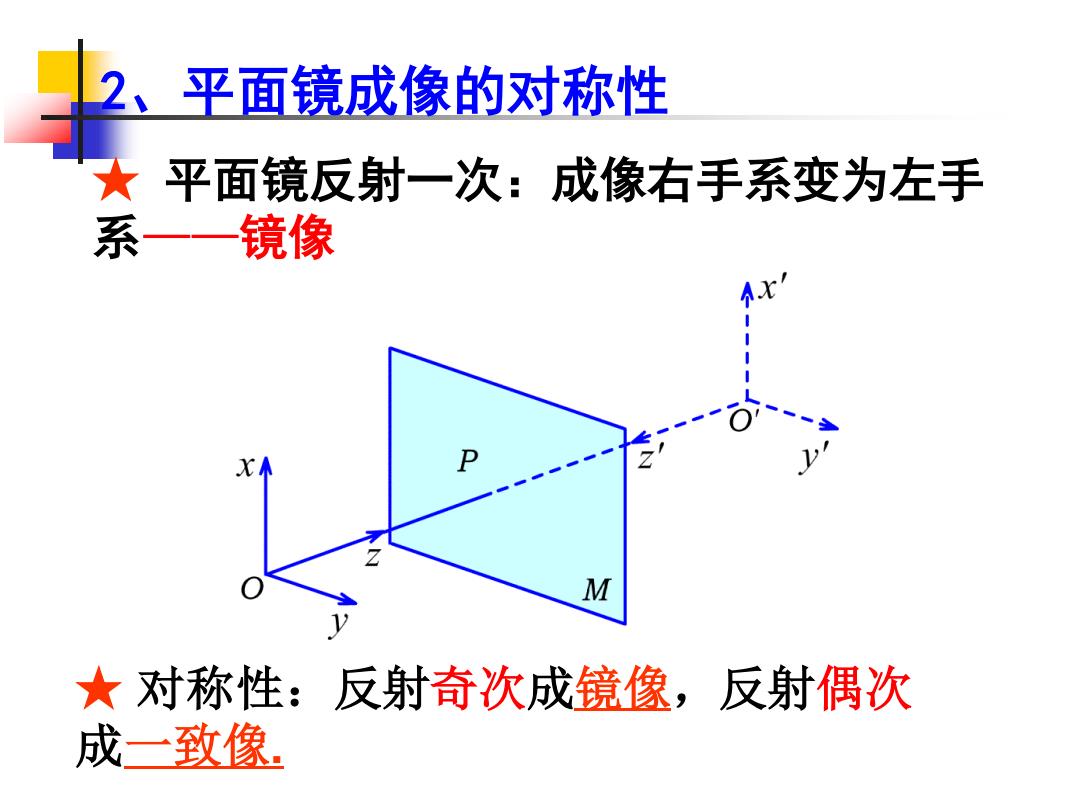
2、平面镜成像的对称性 ★平面镜反射一次:成像右手系变为左手 系一一镜像 M ★对称性:反射奇次成镜像,反射偶次 成一致像
2、平面镜成像的对称性 ★ 平面镜反射一次:成像右手系变为左手 系——镜像 ★ 对称性:反射奇次成镜像,反射偶次 成一致像
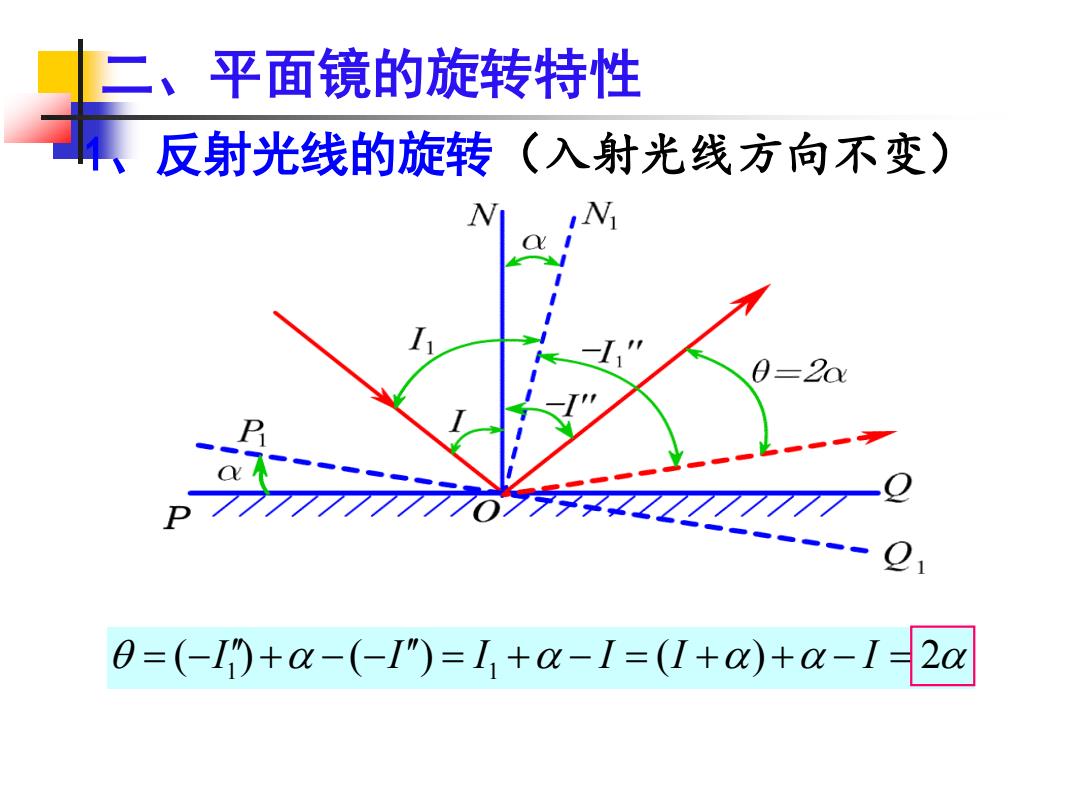
二、平面镜的旋转特性 反射光线的旋转(入射光线方向不变) 0=2a 0=(-I9+a-(-I")=I+a-I=(I+a)+a-I2a
二、平面镜的旋转特性 1、反射光线的旋转(入射光线方向不变) 1 1 = − + − − = + − = + + − = ( ) ( ) ( ) 2 I I I I I I
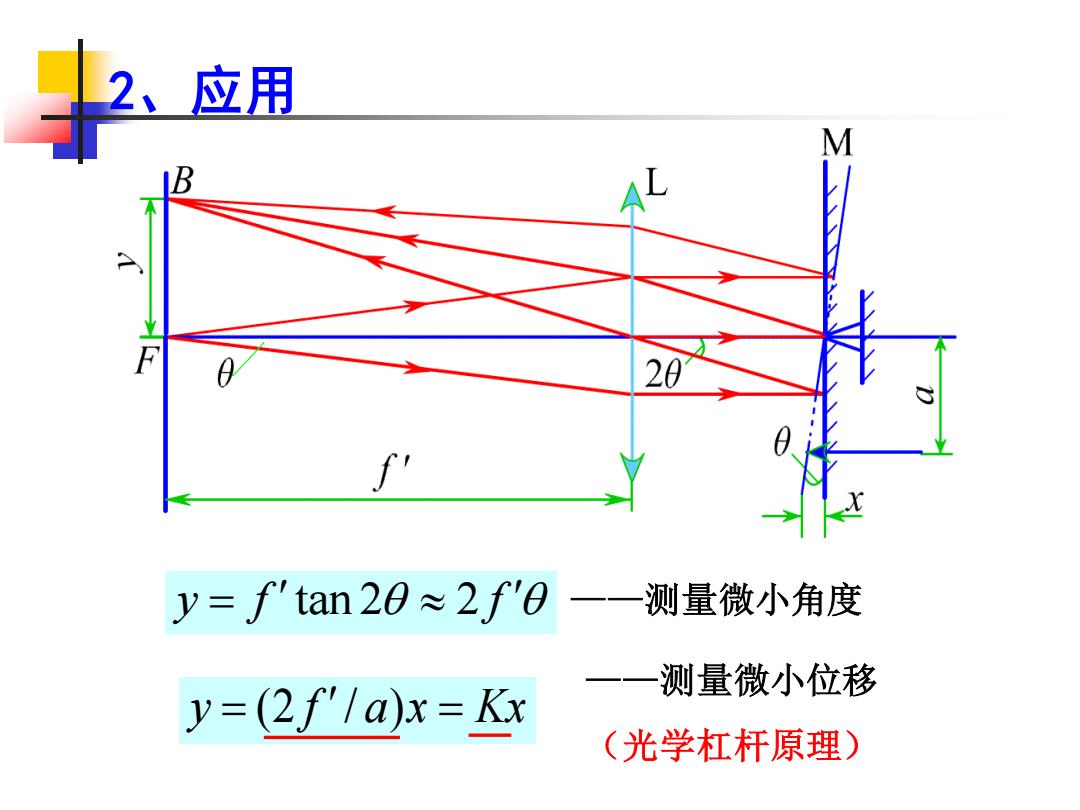
2、应用 y='tan20≈2f'0 一一测量微小角度 测量微小位移 y=(2f/a)x=Kx (光学杠杆原理)
2、应用 y f f = tan 2 2 ——测量微小角度 y f a x Kx = = (2 / ) ——测量微小位移 (光学杠杆原理)

三、双平面镜成像 成像特点:绕棱旋转双镜时,出射光线方向不变。 1)在△O,O2M中,B+(π-2I)+212=π (-I1+I=(I2-I2")+B B=2(I"-12) 2)在△O,O,N中, I"=a+12 B=20x R
三、双平面镜成像 2( ) 1 2 = − I I 2)在O O N 1 2 中, 1 2 I I = + 1、成像特点:绕棱旋转双镜时,出射光线方向不变。 1)在 + − + = OO M I I 1 2 1 2 中, 2 2 ( ) 1 1 2 2 ( ) ( ) − + = − + I I I I = 2
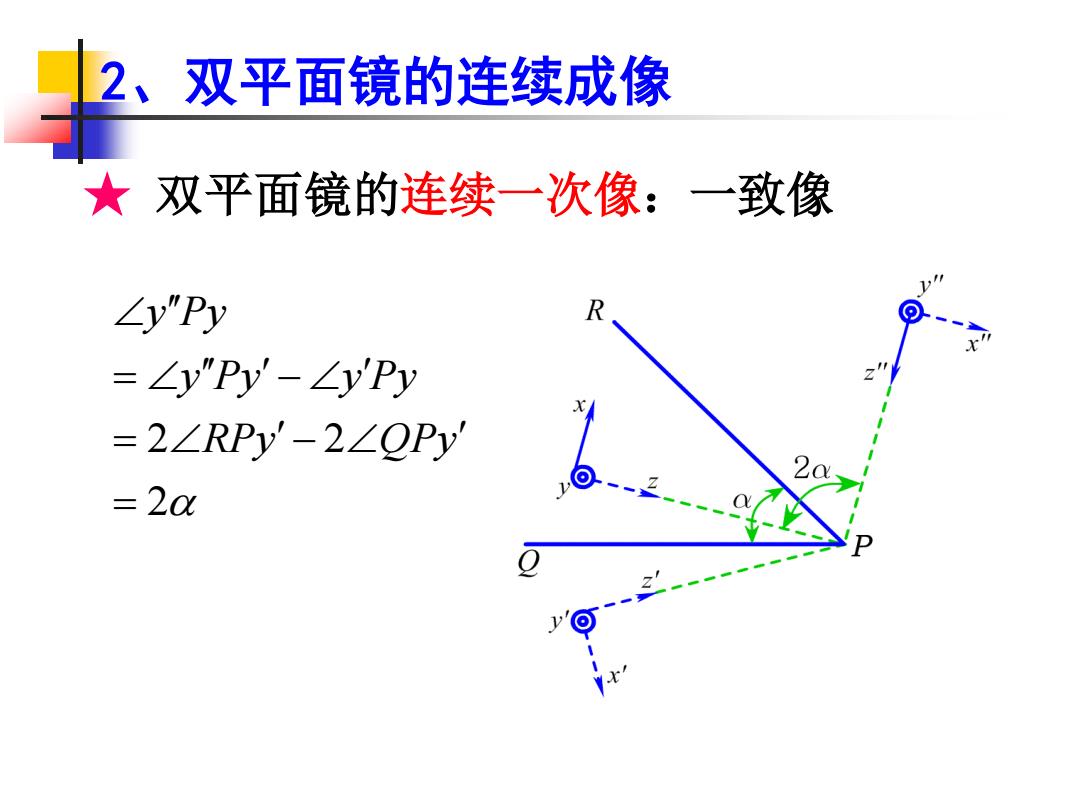
2、双平面镜的连续成像 ★双平面镜的连续一次像:一致像 ∠y'"Py =∠y"Py'-∠y'Py =2∠RPy'-2∠QPy' =20
2、双平面镜的连续成像 2 2 2 y Py y Py y Py RPy QPy = − = − = ★ 双平面镜的连续一次像:一致像

结论 ★连续一次像:物体绕棱边旋转2α角, 旋转方向从第一反射镜转向第二反射镜
★ 连续一次像:物体绕棱边旋转 角, 旋转方向从第一反射镜转向第二反射镜。 2 结论
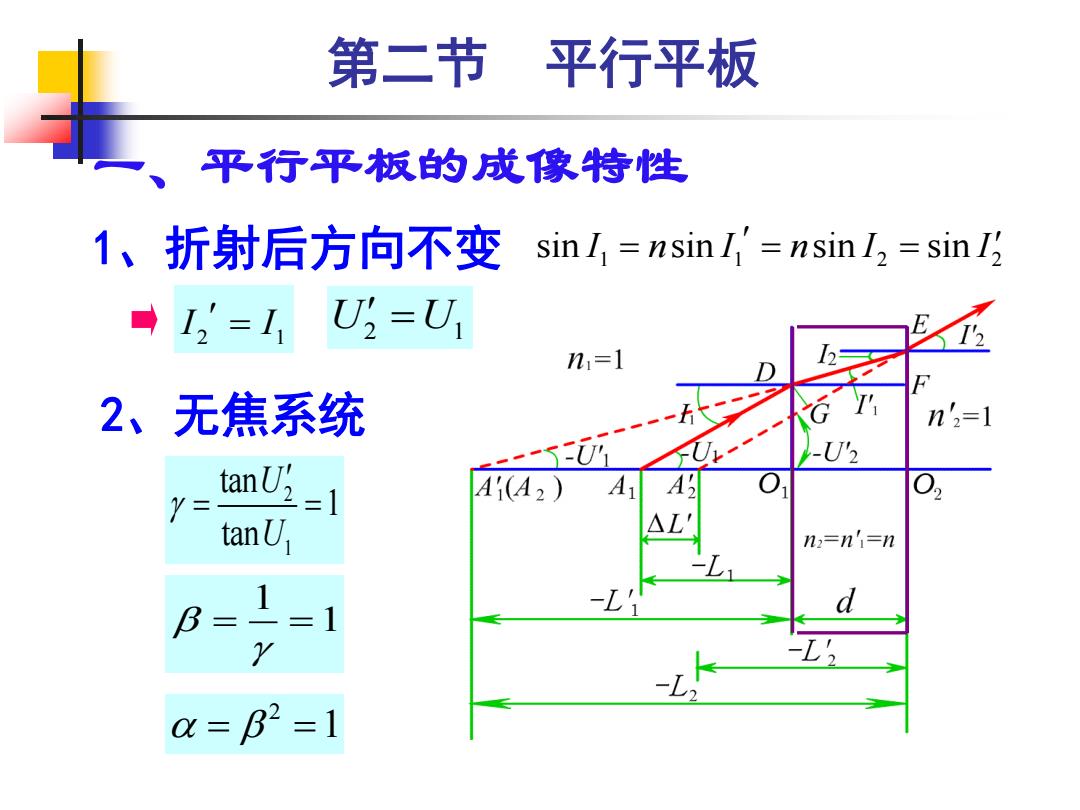
第二节 平行平板 平行平板的成像特性 1、折射后方向不变sinl,=nsinI-nsinI2=sinI; '-1,U=U n1=1 2、无焦系统 n'2=1 --5U乃 U -U'2 A A Y= tanU2=1 A1(A2) tan U, n:=n=n B=1=1 a=B2=1
第二节 平行平板 一、平行平板的成像特性 1 1 2 2 sin sin sin sin I n I n I I 1、折射后方向不变 = = = 2、无焦系统 2 = =1 2 1 tan 1 tan U U = = 1 1 = = 2 1 I I = U U 2 1 =