安徽科技学院：《大学物理》课程教学资源（PPT课件）力学——第三章 动量和角动量

大学 物理 第三章动量和角动量 §3.1动量定理 (Theorem of Momentum) 牛Ⅱ对时间的积分 1.力的冲量(impulse) Fdt—dt内的冲量 I=0)dtt内的冲量 2.质点的动量定理

§3.1 动量定理 (Theorem of Momentum) ——牛Ⅱ对时间的积分 1.力的冲量(impulse) Fdt  —— dt内的冲量  = 2 1 ( ) t t I F t dt   —— t1~t2内的冲量 2.质点的动量定理 第三章 动量和角动量 2 大学 物理

大学 物理 ()微分形式： Fdt dP 2)积分形式：Fd=p-乃 Notes: ①牛Ⅱ一力的瞬时作用 动量定理 一力的持续作用 ②定理的分量形式： F.dt dps " [F,dt=Px -Px

①牛Ⅱ——力的瞬时作用 动量定理——力的持续作用 Notes: (2)积分形式： 2 1 2 1 Fdt P P t t    = −  ②定理的分量形式： Fx dt = dPx ,  2 1 , 2 1 x x t t Fx dt = P − P  (1)微分形式： Fdt dP   = 3 大学 物理

大学 物理 ③平均力： B-P t2-t1t2-t1

③平均力： 2 1 2 1 t t Fdt F t t − =    2 1 2 1 t t P P − − =   4 大学 物理

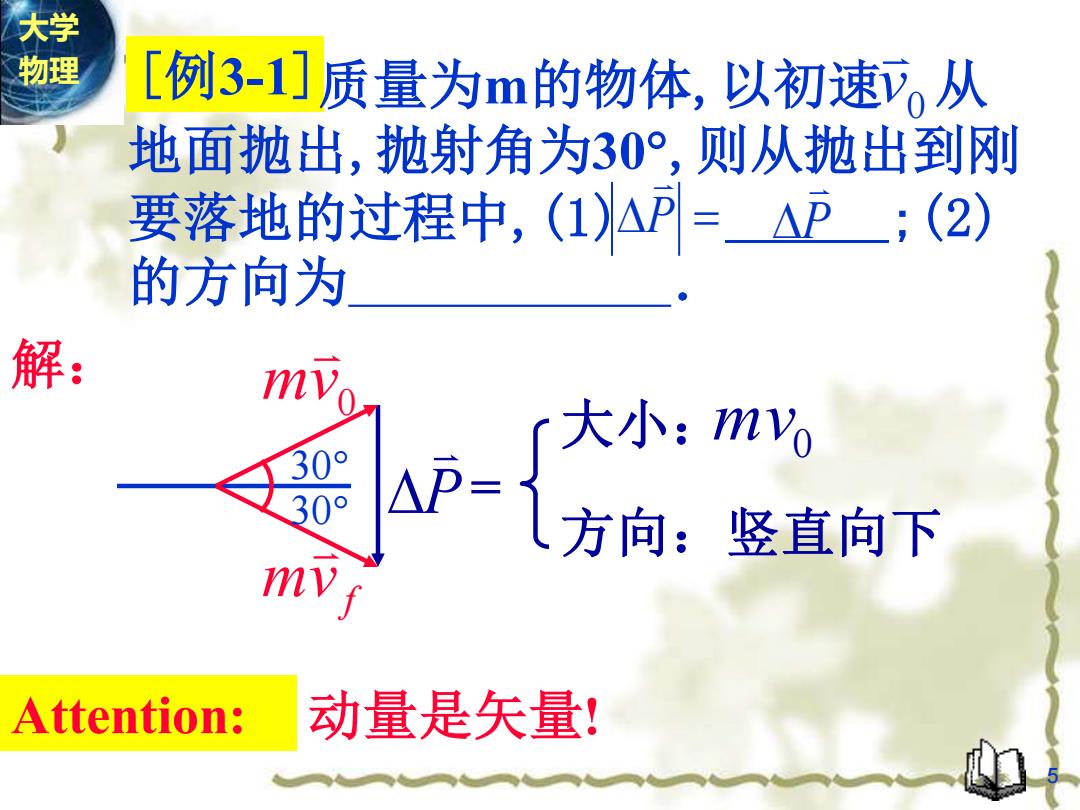
大学 物理 [例3-1]质量为m的物体，以初速从 地面抛出，抛射角为30°，则从抛出到刚 要落地的过程中，(1)AP=△P;(2) 的方向为 解： mvo AP-1 mv Attention: 动量是矢量！

[例3-1] 解： P   Attention: 动量是矢量! 质量为m的物体,以初速 从 地面抛出,抛射角为30 ,则从抛出到刚 要落地的过程中,(1) ;(2) 的方向为 ． 0 v  P =  P   方向：竖直向下 大小： mv0 = 30 30 0 mv  f mv  5 大学 物理

大学 物理 [例3-2]力F=12ti(S)作用在质量 m=2kg的物体上，使之从静止开始运动， 则物体在3秒末的动量应为 解：由动量定理，有 心=E-P=万 →p=i12tdt=54kgm/s 「思考1其它解法？

[例3-2] 力 作用在质量 m=2kg的物体上,使之从静止开始运动, 则物体在3秒末的动量应为 ． F 12ti (SI)   = 解：由动量定理，有 2 1 2 1 Fdt P P t t    = −   → = 3 0 P2 i 12tdt   [思考]其它解法？ P2  = = 54i k gm/s  6 大学 物理

大学 物理 §3.2动量守恒定律 (The Law of Conservation of Momentum) 1.质点系的动量定理 系统所受合 系统总动 外力的冲量 量的增量

§3.2 动量 守恒定律 (The Law of Conservation of Momentum) Fextdt dP   = 1.质点系的动量定理 系统所受合 外力的冲量 系统总动 量的增量 7 大学 物理

大学 物理 对第个质点，有F,dt=dP 对整个系统，有∑F,dt=∑d 其中 ∑F,di=(∑万am+∑fnr)dh =(∑fa)dt ∑dp=d(∑p)=dp ●●●●●●●●

[证] 对第i个质点，有 Fi dt dPi   = 对整个系统，有  = i i Fi dt dPi    =  + i i i ext i i i Fdt ( F F )dt , ,int    其中 F dt i i ext ( ) =  ,  F dt ext  = dP d P dP i i i i     = ( ) =  8 大学 物理

大学 物理 Attention: 内力的作用可以改变系统的 总动能，但却不能改变系统的总动量！ 2.动量守恒定律 对于质点系，若 =0 则P=const. Notes: (1)动量定理和动量守恒定律也只是在 惯性系中成立

内力的作用可以改变系统的 总动能,但却不能改变系统的总动量! Attention: 2.动量守恒定律 对于质点系，若 Fext = 0  则 P = const.  ⑴动量定理和动量守恒定律也只是在 惯性系中成立． Notes: 9 大学 物理

大学 物理 2)分量形式： e.g.若 =0 则P =const. (3)在碰撞、爆炸、子弹射入等情形 可忽略外力冲量的影响，认为 P=const

⑵分量形式： 若 0 Fext,x = 则 P const. x = e.g. ⑶在碰撞、爆炸、子弹射入等情形, 可忽略外力冲量的影响, 认为 P = const.  10 大学 物理

大学 物理 [例3-3]光滑水平面上有两个小球A和 B,A静止，B以速度立和A碰撞.碰 后，B的速度大小为v/2,方向与垂 直，求碰后A球的运动方向. 解：A一B系统，在水平面内P=const. mev' 如图，tg0=v1v=号→0=26.6

解：A－B系统，在水平面内 P = const.  m vB  m vB   m vA    如图， 2 1 tg = v / v =  →  = 26.6 [例3-3]光滑水平面上有两个小球A和 B，A静止，B以速度 和A碰撞．碰 后，B的速度大小为 ，方向与 垂 直，求碰后A球的运动方向． v  v  v / 2 11 大学 物理