
第八章1 静电场中的导体和电介质 (Conductors and Dielectrics in Electrostatic Field) 内容: 导体的静电平衡 电介质的极化 D的高斯定理 电容器与电容 静电场的能量
第八章 静电场中的导体和电介质 (Conductors and Dielectrics in Electrostatic Field) 导体的静电平衡 电介质的极化 的高斯定理 电容器与电容 静电场的能量 内容: D

S8.1导体的静电平衡Electrostatic Equilibrium of Conductors) 导体内部和表面都没有电荷定向移 动的状态 1.静电平衡的条件 E内=0 E表⊥表面
1.静电平衡的条件 §8.1 导体的静电平衡(Electrostatic Equilibrium of Conductors) ——导体内部和表面都没有电荷定向移 动的状态 ⊥ = 表 表面 内 E E 0

2.静电平衡下的性质 (1)实心导体 ①关于Q i)Q仅分布于表面 理由:在导体内任取一体积元 则有fES=0→∑9纳=0 ·体积元大小和位置任意 ∴导体内处处没有净电荷
2.静电平衡下的性质 ⑴实心导体 ①关于Q 理由:在导体内任取一体积元 = 0 → q 内 = 0 S E dS 则有 ∵体积元大小和位置任意 i)Q仅分布于表面 ∴导体内处处没有净电荷
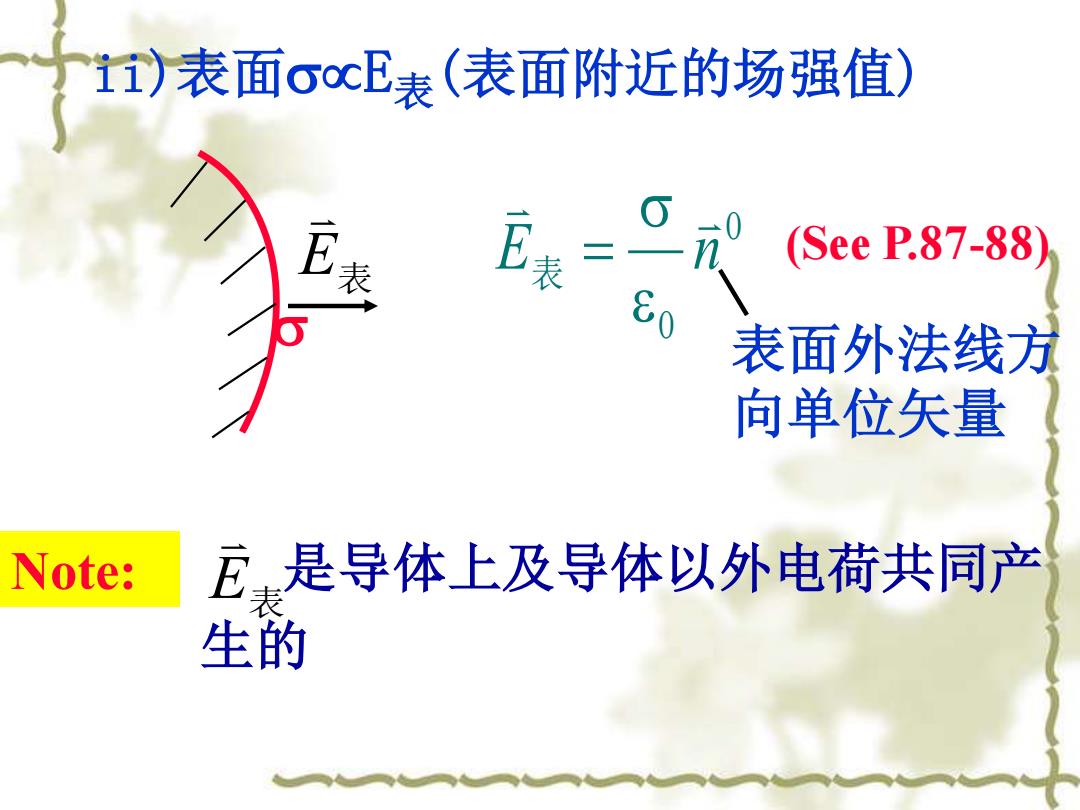
11)表面oocE表(表面附近的场强值) (SeeP.87-88) 表面外法线方 向单位矢量 Note: E是导体上及导体以外电荷共同产 生的
ii)表面E表(表面附近的场强值) 0 0 E n = 表 是导体上及导体以外电荷共同产 生的 E表 Note: (See P.87-88) 表面外法线方 向单位矢量 E表
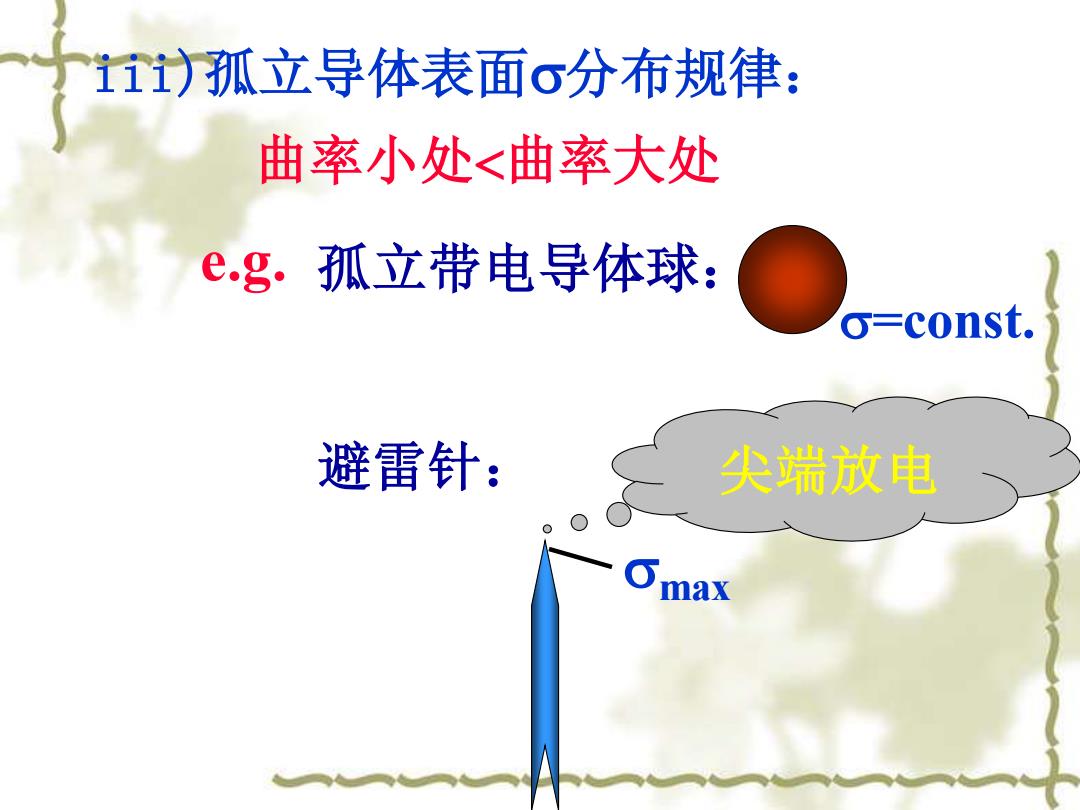
ii)孤立导体表面o分布规律: 曲率小处<曲率大处 eg.孤立带电导体球: o=const. 避雷针: 尖端放电
iii)孤立导体表面分布规律: 曲率小处曲率大处 孤立带电导体球: =const. 避雷针: 尖端放电 e.g. max

②关于V 整个导体是等势体 理由:在导体内任取两点A、B 则有V4-s=Ei=0 ..V=VB Note: “导体是等势体” 静电平衡条件 的另一种表述
②关于V 理由:在导体内任取两点A、B 则有 − = = 0 B A A B V V E dl VA =VB ——整个导体是等势体 “导体是等势体”——静电平衡条件 的另一种表述 Note:
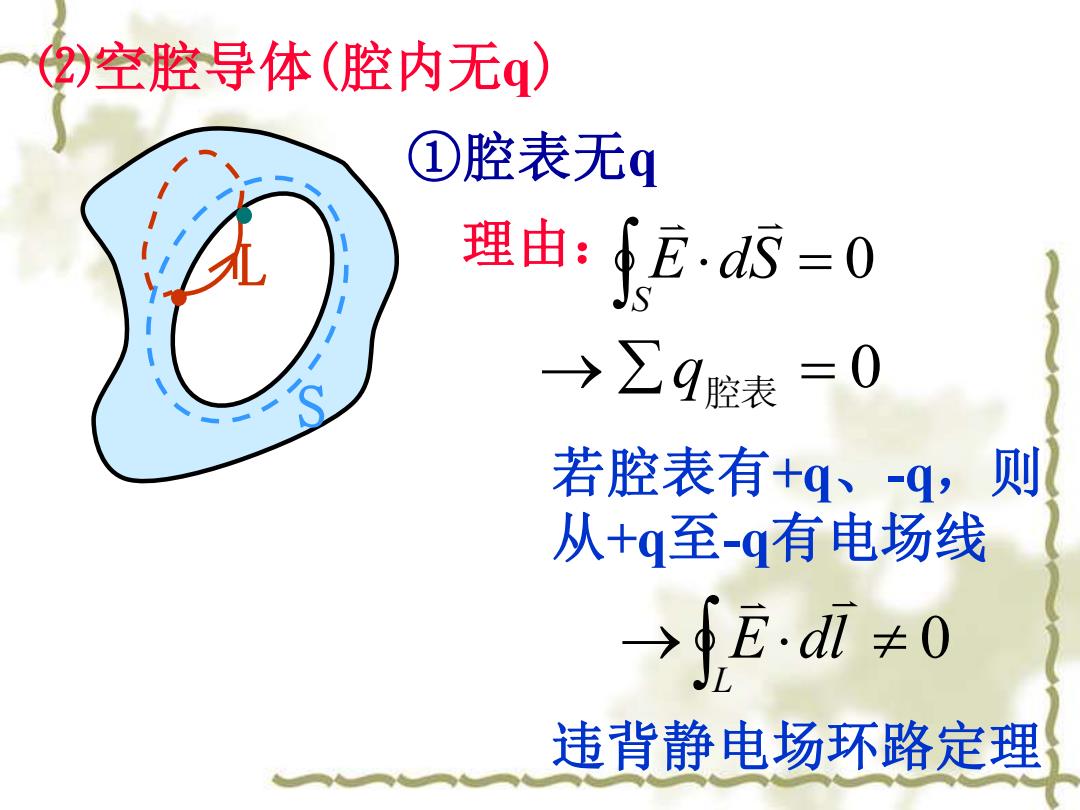
2)空腔导体(腔内无q) ①腔表无q 理由:fES=0 →∑9腔表=0 若腔表有+q、-q,则 从+q至-q有电场线 →fE通≠0 违背静电场环路定理
⑵空腔导体(腔内无q) ①腔表无q 理由: S = 0 S E dS → q 腔表 = 0 若腔表有+q、-q,则 从+q至-q有电场线 → 0 L E dl 违背静电场环路定理 L
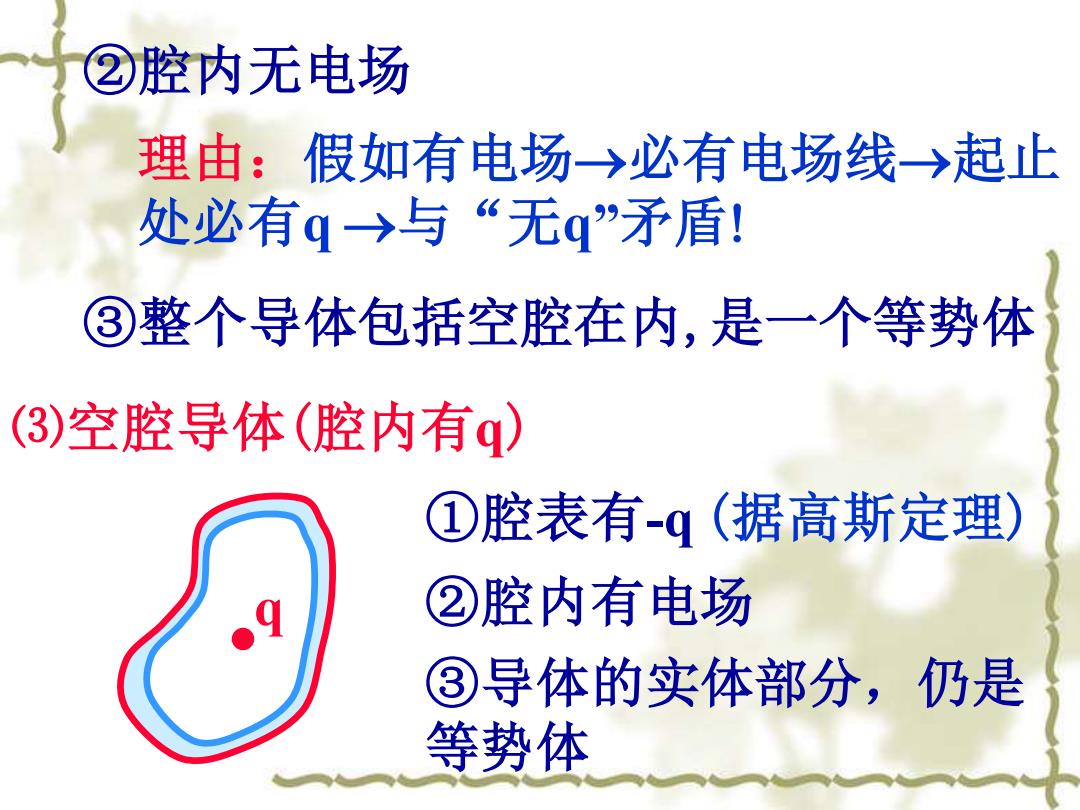
②腔内无电场 理由:假如有电场→必有电场线→起止 处必有q→与“无q”矛盾! ③整个导体包括空腔在内,是一个等势体 (3)空腔导体(腔内有q) ①腔表有-q(据高斯定理) ②腔内有电场 ③导体的实体部分,仍是 等势体
②腔内无电场 理由:假如有电场→必有电场线→起止 处必有q →与“无q”矛盾 ③整个导体包括空腔在内,是一个等势体 ⑶空腔导体(腔内有q) ①腔表有-q (据高斯定理) ②腔内有电场 ③导体的实体部分,仍是 等势体 q
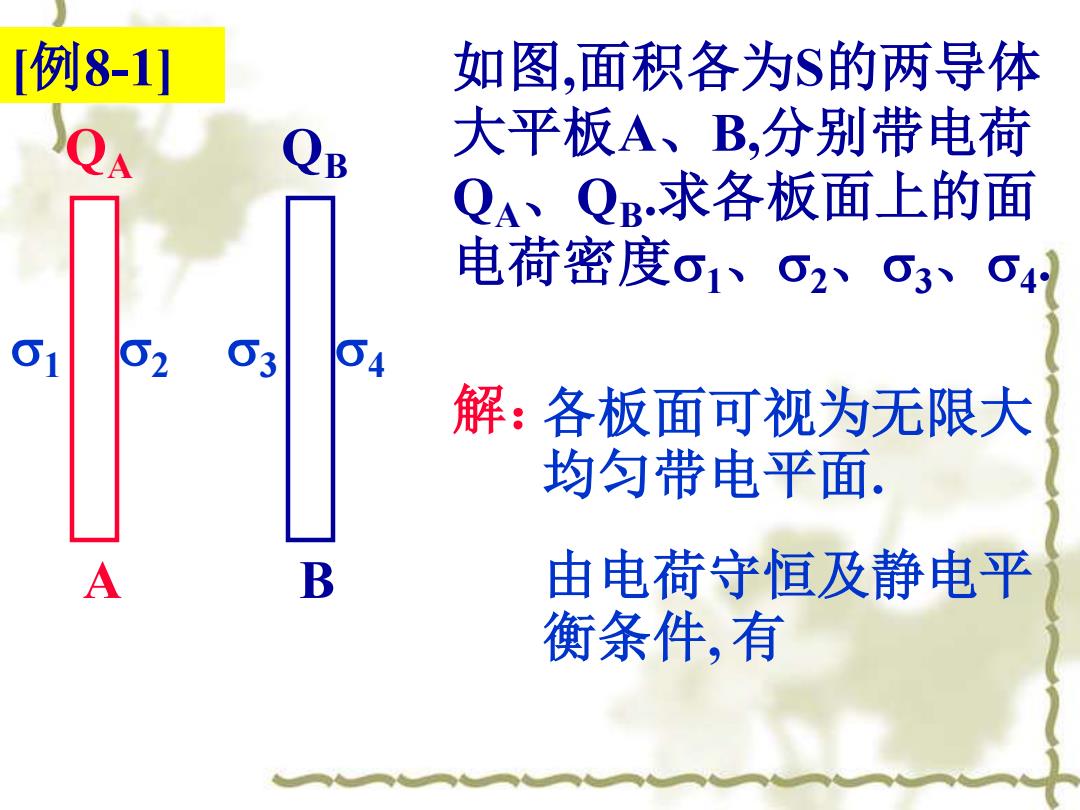
[例8-1] 如图,面积各为S的两导体 大平板A、B,分别带电荷 A B QA、QB求各板面上的面 电荷密度σ1、2、3、4 可1 62 3 解:各板面可视为无限大 均匀带电平面. A B 由电荷守恒及静电平 衡条件,有
[例8-1] 1 2 3 4 QA QB A B 如图,面积各为S的两导体 大平板A、B,分别带电荷 QA、QB .求各板面上的面 电荷密度1、2、3、4 . 解:各板面可视为无限大 均匀带电平面. 由电荷守恒及静电平 衡条件, 有

o1+o2=Q4/S ① (Q=const.) o3十o4=QB/S (QB=const.) 61-02-03-04=0 ③ (EA=0) 01+02十03-04=0 ④ (EB=0) ③④→ 01-04=0 (外侧 等量同号!) 0203=0 ⑥ (内侧 等量异号!)
1+2=QA/S ① (QA=const.) ③④→ 1 -4=0 ⑤ 2+3=0 ⑥ (外侧——等量同号!) (内侧——等量异号!) 3+4=QB /S ② (QB=const.) 1 -2 -3 -4=0 ③ (EA=0) 1+2+3 -4=0 ④ (EB=0)