
第四章 刚体的定轴转动 (Rotation of a Rigid Body About a Fixed Axis) 刚体:任意两质元间距离保持不变.(理想模型) 刚体的运动: ①平动- 各质元运动状态保持相同 ②转动一各质元绕同一轴作圆周运动 ③复合运动—平动十转动
第四章 刚体的定轴转动 (Rotation of a Rigid Body About a Fixed Axis) 刚体:任意两质元间距离保持不变.(理想模型) 刚体的运动: ③复合运动——平动+转动 ①平动——各质元运动状态保持相同 ②转动——各质元绕同一轴作圆周运动

本章:(定轴转动运动学 定轴转动定律 转动中的功和能 定轴转动的角动量守恒定律
本章: 定轴转动运动学 定轴转动定律 转动中的功和能 定轴转动的角动量守恒定律

S4.1定轴转动运动学(Kinematics of Rotation About a Fixed Axis) 同“圆周运动” S = RO V= Ro a, Ra an = Ro 2
§4.1 定轴转动运动学 (Kinematics of Rotation About a Fixed Axis) ——同“圆周运动” v s R o t a n a S = R v = R at = R 2 an = R
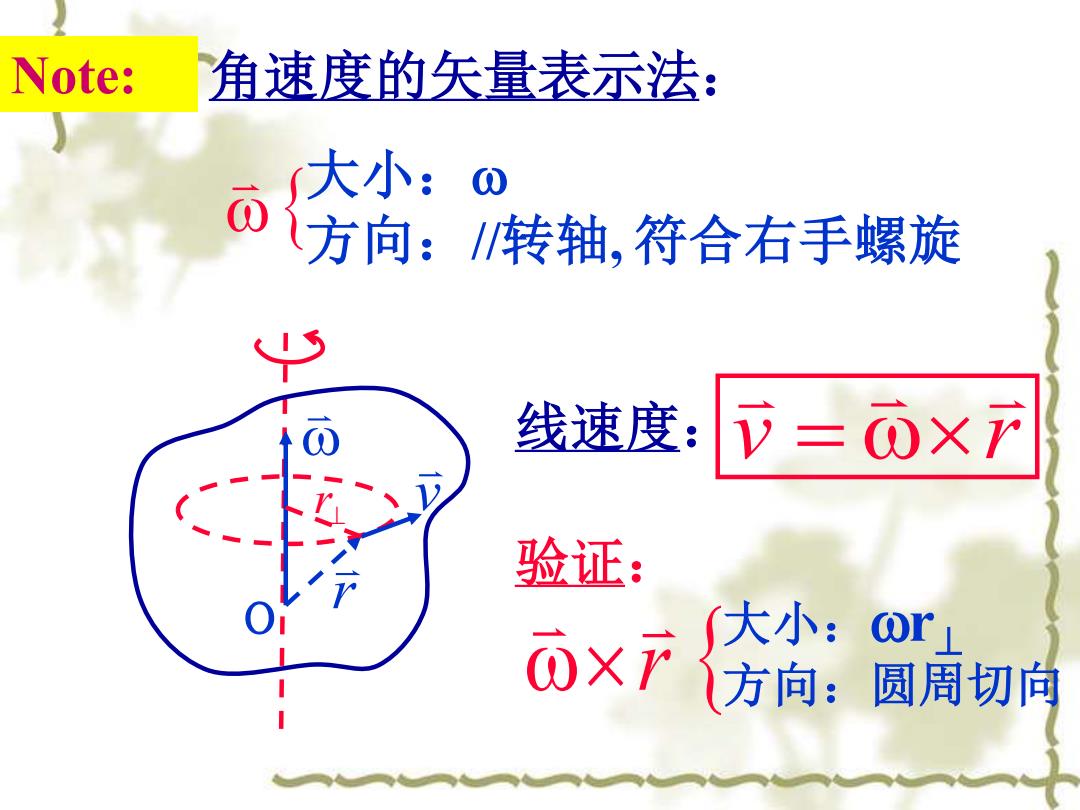
Note: 角速度的矢量表示法: 大小:0 方向:/转轴,符合右手螺旋 线速度: 验证: O×F 大小:Or 方向:圆周切向
角速度的矢量表示法: 大小: 方向://转轴, 符合右手螺旋 O r ⊥ r v 线速度: v r = 验证: r 大小:r⊥ 方向:圆周切向 Note:

例4-1已知:o=60 k rev/min F=(3i+4i+5k)×102m 求:立=? 解:o=(60×2π/60)k=2成(rad/) 立=ōXF =2πk×(3i+4j+5k)×103 =(60-8m)×102 0.251i+0.188j(m/s)
例4-1 已知: 60k rev / min = r i j k m 2 (3 4 5 ) 10− = + + 求: v = ? 解: k = (602 / 60) 2 k (rad /s) = v r = 2 2 (3 4 5 ) 10− = k i + j + k 2 (6 8 ) 10− = j − i 0.251i 0.188 j (m/s) = − +
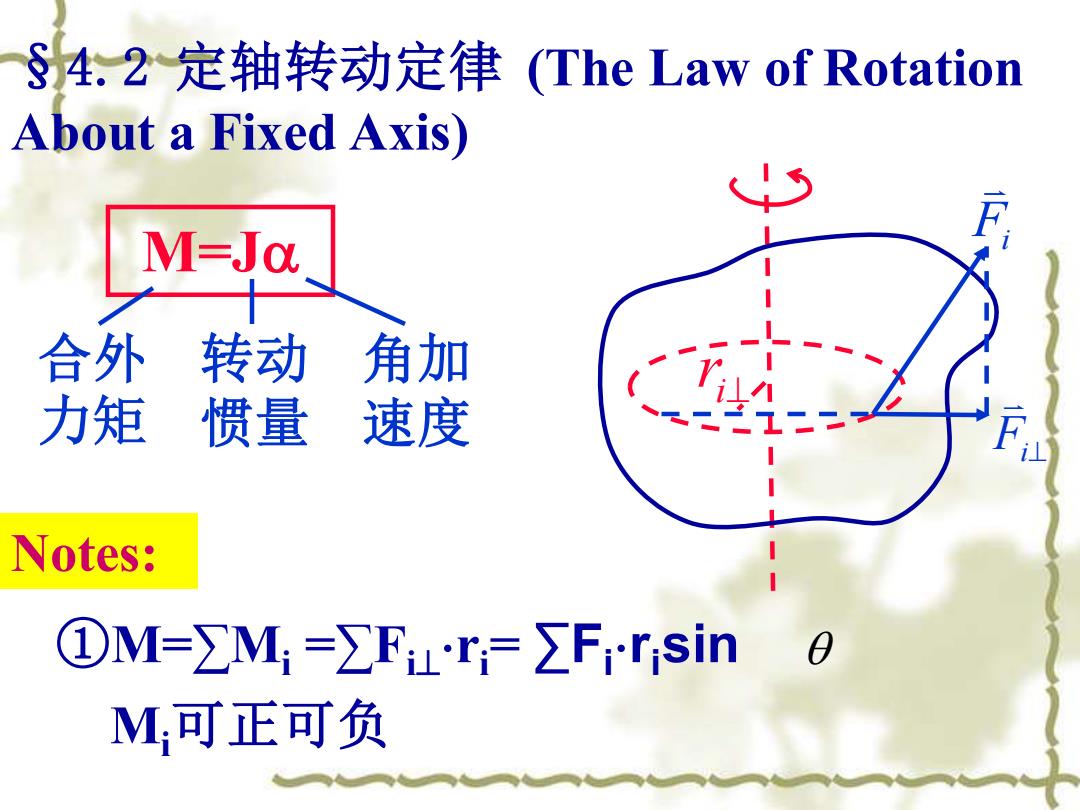
S4.2定轴转动定律(The Law of Rotation About a Fixed Axis) M=Ja 合外 转动 角加 力矩 惯量 速度 Notes: ①M=∑M=∑F4r=∑Frr;sin M,可正可负
§4.2 定轴转动定律 (The Law of Rotation About a Fixed Axis) M=J ①M=∑Mi =∑Fi⊥ ri= ∑Fi risin 合外 力矩 转动 惯量 角加 速度 Notes: i⊥ r Fi Fi⊥ Mi可正可负
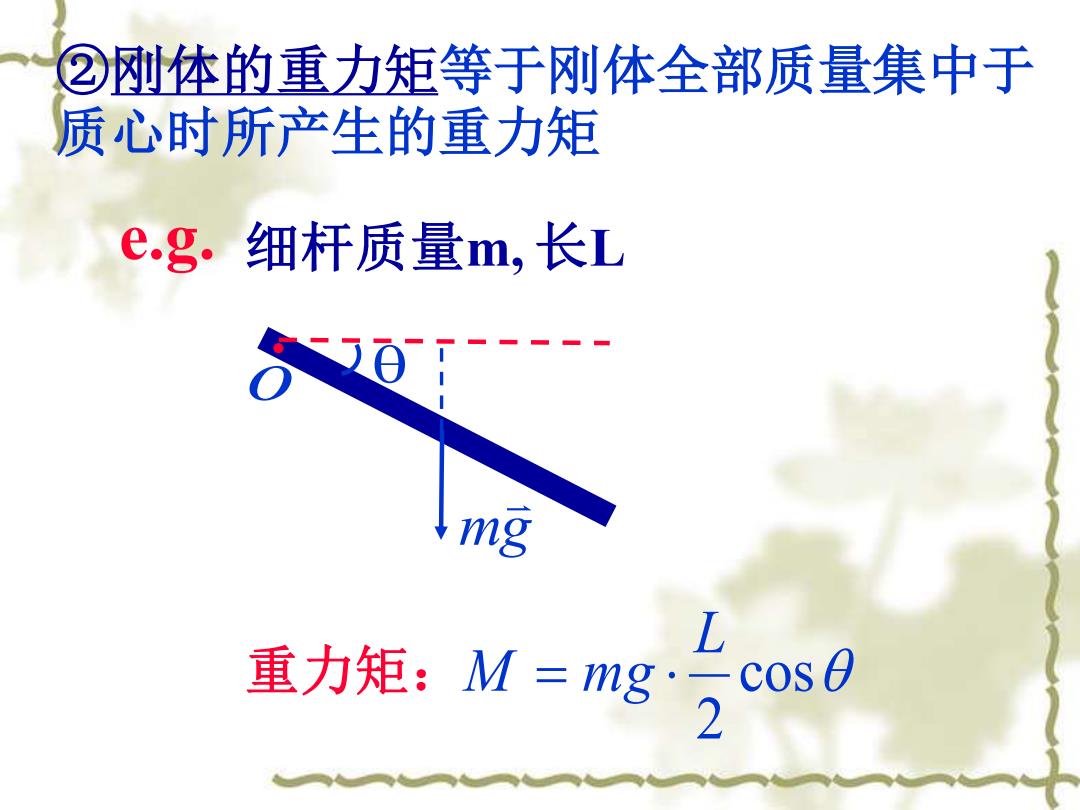
②刚体的重力矩等于刚体全部质量集中于 质心时所产生的重力矩 e.g.细杆质量m,长L 50 mg 重力短:M=mg2 cos 0
②刚体的重力矩等于刚体全部质量集中于 质心时所产生的重力矩 o mg 重力矩: cos 2 L M = mg e.g. 细杆质量m, 长L
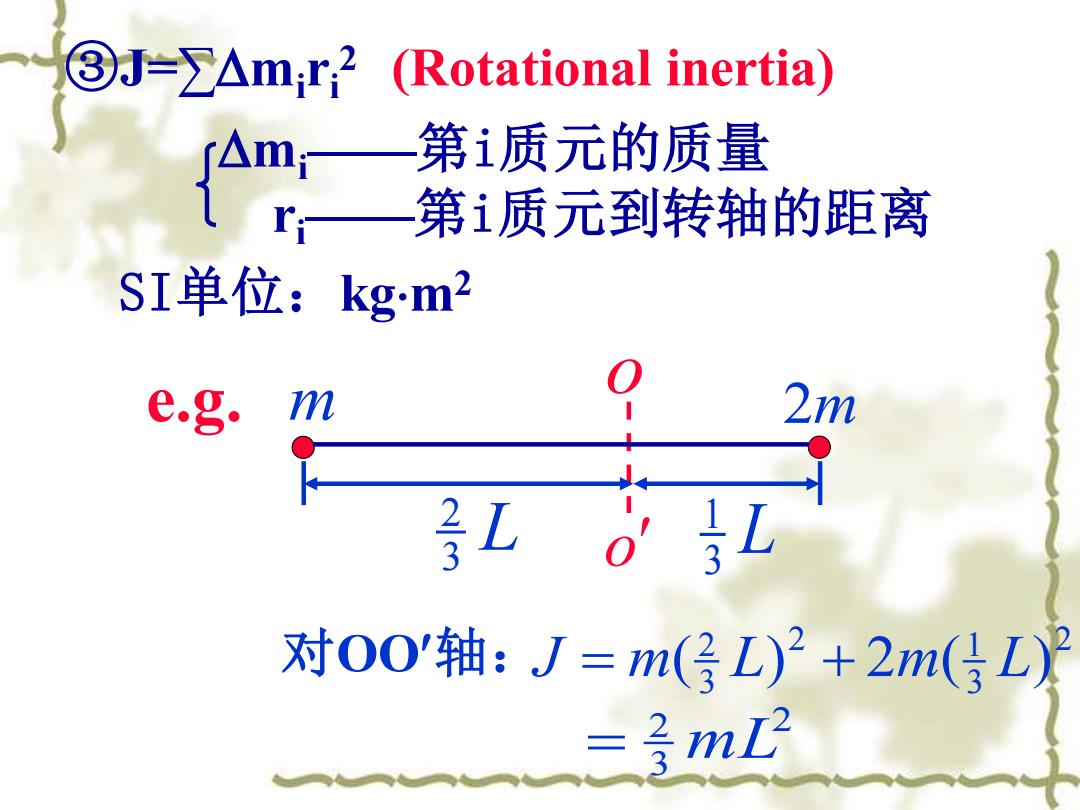
③J=∑△mr2(Rotational inertia) 第i质元的质量 第i质元到转轴的距离 SI单位:kgm2 e.g. n 2m 02 对00'轴:J=m(径L)2+2m(3L)} 子mL乃
③J=∑mi ri 2 (Rotational inertia) mi——第i质元的质量 ri——第i质元到转轴的距离 e.g. o o m 2m L3 2 L3 1 2 3 = 2 mL 2 3 2 1 3 2 对OO轴: J = m( L) + 2m( L) SI单位:kgm2
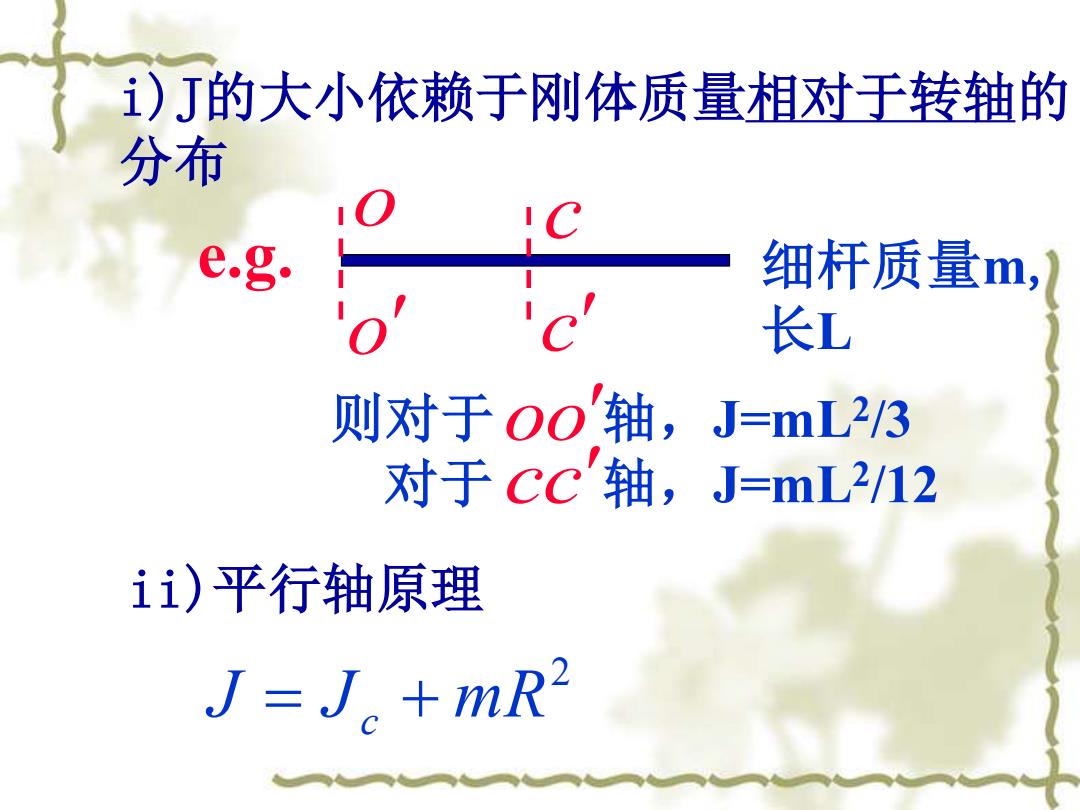
)J的大小依赖于刚体质量相对于转轴的 分布 e.g. 细杆质量m,) 长L 则对于00轴,J=mL23 对于CC'轴,J=mL2/12 ii)平行轴原理 J=J。+mR2
i)J的大小依赖于刚体质量相对于转轴的 分布 o o c c 细杆质量m, 长L 则对于 轴,J=mL2 /3 对于 轴,J=mL2 cc /12 oo e.g. ii)平行轴原理 2 J = Jc + mR

iii)J量度了刚体转动惯性的大小 ④转动定律与牛Ⅱ比较: F ma & ik Sis M=Ja
iii)J量度了刚体转动惯性的大小 ④转动定律与牛Ⅱ比较: M~ J ~ ~ F a m F ma = M = J